水星近日点进动问题
对水星点进动的计算实际上主要是根据牛顿定律进行,结果是每世纪=5,557.62角秒的进动﹐其中的90%是由坐标系的岁差引起﹐其余的部分是由其他行星﹐特别是金星﹑地球和木星的摄动引起的﹔而实际观测值为 =5,600.73角秒﹐二者相减得每世纪 43.11角秒。
中文名 水星近日点进动问题 主要依据 牛顿定律 研究对象 水星 提出者 勒威耶
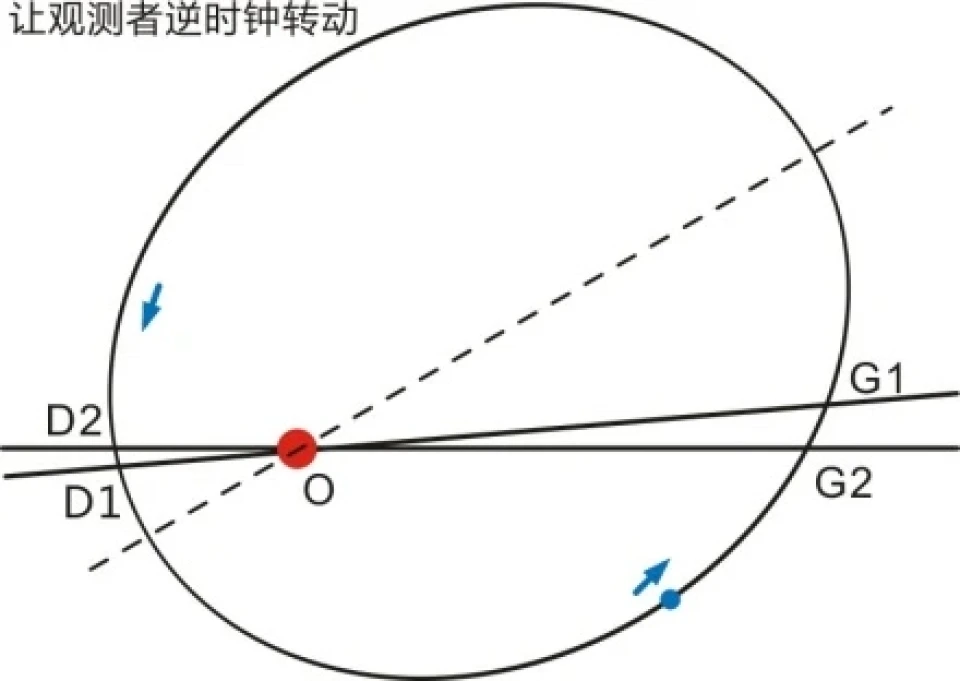
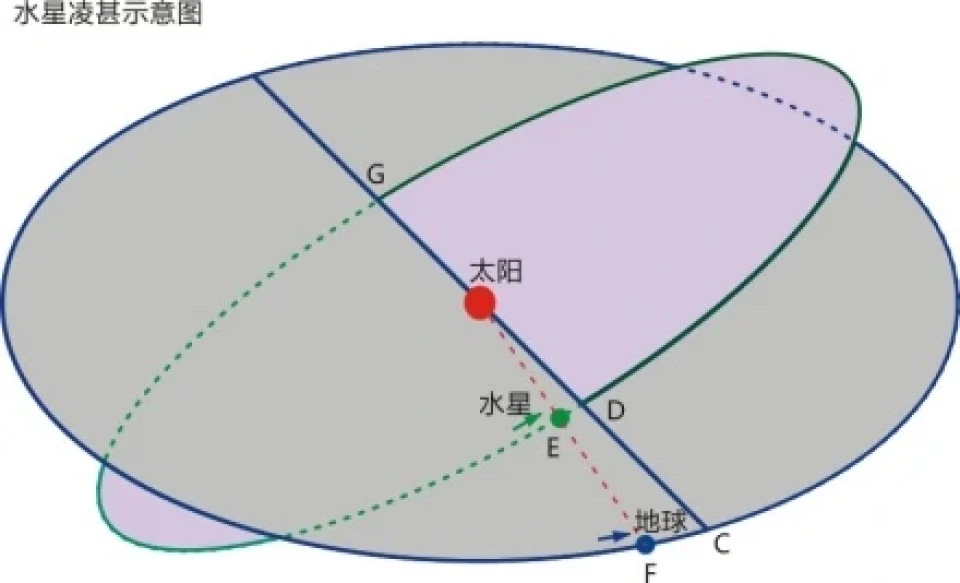
天文测量发现水星在升交点D的公转周期与降交点G的公转周期不一样。经分析是水星轨道绕太阳逆时钟转动,不封闭。
如果让观测者跟随水星轨道逆时钟转动,则观测到的水星轨道“封闭”不进动,观测到的升交点和降交点则顺时钟转动,D1G1一个水星周期后成了D2G2。那么我们观测到升交点D点的周期实际为水星从D1出发到D2的时间,降交交点G点的周期实际为水星从G1到G2的时间。这样就正好解释了两个点周期不相等的原因。
根据牛顿万有引力定律计算的水星近日点进动值与观测值的分歧。1859年﹐法国天文学家勒威耶发现水星近日点进动的观测值﹐比根据牛顿定律算得的理论值每世纪快38"﹐并猜测这可能是一个比水星更靠近太阳的水内行星吸引所致。可是经过多年的辛勤搜索﹐这颗猜测中的行星始终毫无踪影。纽康测定这个值为每世纪 43"。他提出﹐这可能是那些发出黄道光的弥漫物质的阻尼所造成的。但是﹐这种假设又不能解释其他几颗行星的运动。于是纽康就怀疑万有引力定律中的平方反比规律有问题。为了能同时解释几颗内行星的实际运动﹐纽康求出了引力应与距离的2.1574 [1] 次方成反比。十九世纪末﹐电磁理论发展的早期﹐韦伯﹑黎曼等人也都曾试图用电磁理论来解释水星近日点的进动问题﹐但均未能得出满意的结果。
1916年﹐爱因斯坦发表了著名的广义相对论﹐成功地解释了这个问题。根据广义相对论﹐行星公转一圈后近日点进动为﹕
相应公式
相应公式
式中c 为光速﹐T ﹑a ﹑e 分别为轨道周期﹑半长径和偏心率。对于水星﹐此值与牛顿万有引力定律所得的差值为每世纪43.03秒。这与观测值十分接近﹐成为天文学对广义相对论的最有力的验证之一。
但是,这里仍存在两个问题:首先,根据牛顿定律,水星近日点应有每世纪ΔωN=5,557.62角秒的进动,其中的90%是由坐标系的岁差(见岁差和章动)引起,其余的部分是由其他行星,特别是金星、地球和木星的摄动引起的;而实际观测值为 ΔωO=5,600.73角秒,二者相减得每世纪 43.11角秒。因此,岁差常数的任何微小变动,如有万分之一的变动,都会直接影响到对广义相对论的验证,而这种变化是完全可能的。其次,影响水星近日点进动的因素很多,任何一个微小的因素,例如太阳的扁率,对它都有直接影响。因此,这个问题尚需继续研究。
公转
水星的运行轨道是偏心的,半径从 4 600 万公里到 7 000 万公里变化。围绕太阳的缓慢岁差不能完全地被牛顿经典力学所解释,以致于在一段时间内很多人用设想的另外一个更靠近太阳的行星(有时被称为火神星)来解释这个混乱。这称为“水星近日点进动”。然而,爱因斯坦的广义相对论后来提供了一种可以消除这个小误差的解释。
自转
1889年意大利天文学家夏帕里利经过多年观测认为水星自转时间和公转时间都是88天。直到1965年,美国天文学家才测量出了水星自转的精确周期58.646天。 在一些时候,在水星的表面上的一些地方,在同一个水星日里,当一个观测者(在太阳升起时)时观测,可以看见太阳先上升,然后倒退最后落下,然后再一次的上升。这是因为大约四天的近日点周期,水星轨道速度完全地等于它的自转速度,以致于太阳的视运动停止,在近日点时,水星的轨道速度超过自转速度;因此,太阳看起来会逆行性运动,在近日点后的四天,太阳恢复正常的视运动。
成果
直到1965年使用雷达观测后,观察数据否决了水星对太阳是潮汐固定的的想法:自转使得所有时间里水星保持相同的一面对着太阳。水星轨速振谐为3:2 ,这就是说自转三次的时间是围绕太阳公转两次的时间;水星的轨道离心使这个谐振持稳。最初天文学家认为它有被固定的潮汐是因为水星处于最好的观测位置,它总是在 3:2 谐振中的相同时刻,展现出相同的一面,就如同它完全地被固定住一样。水星的自转比地球缓慢 59 倍。
因为水星的 3:2 的轨速比率, 一个恒星日 (自转的周期) 大约是58.7个地球日,一个太阳日(太阳穿越两次子午线之间的时间)大约是176个地球日。













请登录之后再进行评论