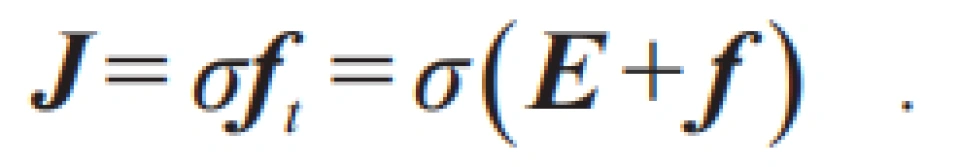为简单起见,我们先探讨最简单的“稳恒电流”,即电路中的电流不随时间变化的情况。从物理机制上来讲,导体中的电流如何流动的规律被总结为“微分形式的欧姆定律”:
导体中的电流密度J(单位时间单位面积流过的电荷量)与单位(正)电荷受到的合力ft=F/q成正比,比例因子称为“电导率”,记作σ。
一般情形下,电导率是张量(张量概念是矢量概念的推广,矢量是一阶张量。
张量是一个可用来表示在一些矢量、标量和其他张量之间的线性关系的多线性函数),如果电流密度与合力方向一致,电导率是一个标量,等于电阻率ρ的倒数。
为叙述方便,还经常将单位电荷所受的合力拆分为静电场E(静电场的定义即为单位电荷受到的静电力)和非静电力f。微观形式的欧姆定律的数学表达式即为:
常见的非静电力有化学电源中的化学作用,发电机中的磁力,浓度不均的体系中的扩散作用,温差电效应等等,它们都可以严格或近似地用单位电荷所受到的力来描述,如:
1、磁力:f = u×B,其中u是导体在磁场中做切割磁感线运动的速度;
2、温差电(Seebeck效应):f = -S∇T,其中S是Seebeck系数,T是温度。
在这里,我们要澄清一个比较容易被误解的点:一些同学学习到电流和电路这一章节的时候,将其与之前所学的静电场的内容完全割裂开了。通过上述的欧姆定律,我们清晰地看到:在电路中驱动电荷做定向流动的是静电场E与单位电荷所受的非静电力f这两者;而在一般的电路中,非静电力仅在电源内部(内电路)存在。
因此在整个外电路中,驱动电荷运动的只是静电场本身。
这个静电场是哪里来的呢?
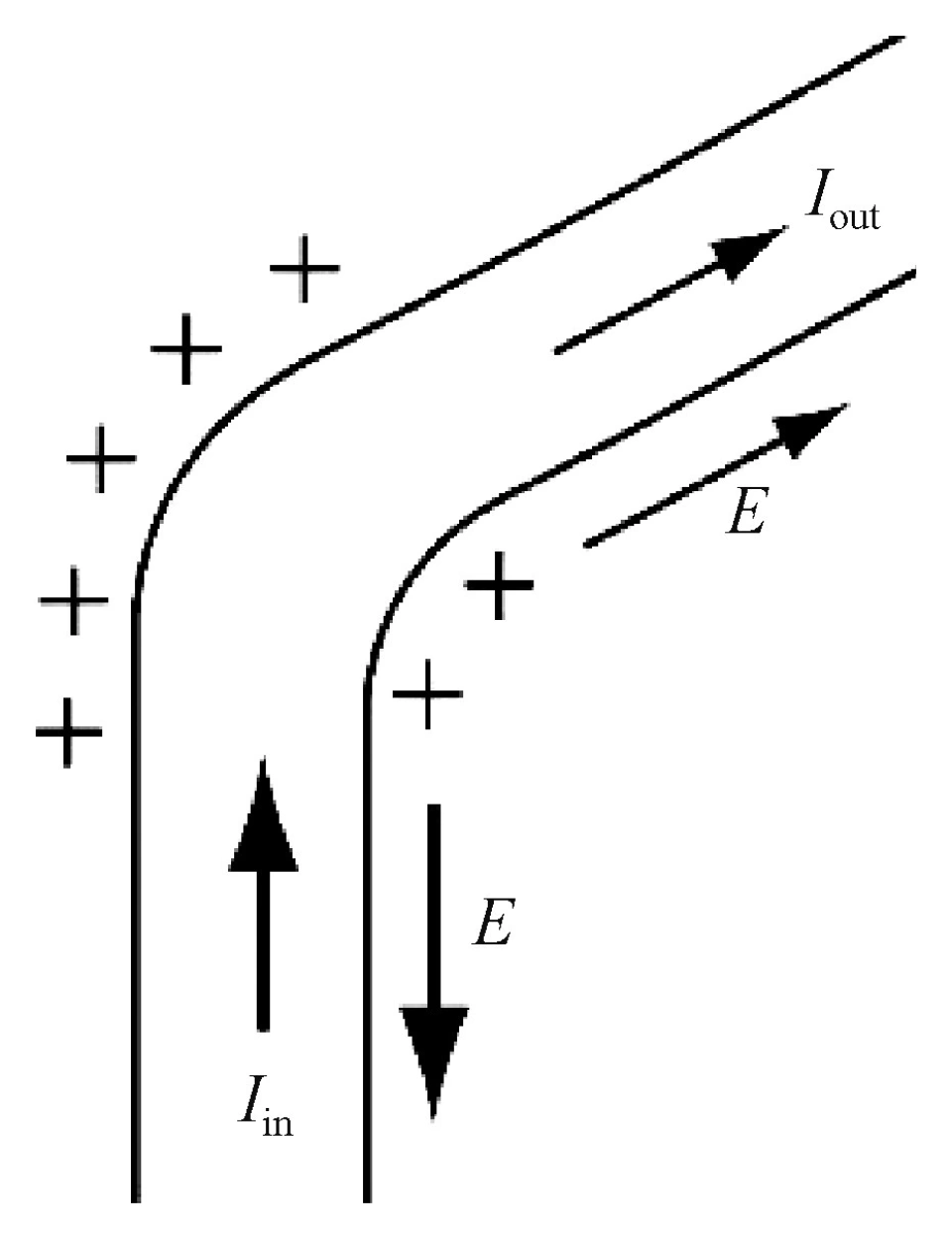
答案其实非常有意思,它与我们在初中第一次学习电路时就知道的一个事实“稳恒电路中同一根导线中的电流处处相等”息息相关。设想如图1所示的一段电路,如果一开始流入拐角处的电流大于流出的,即Iin>Iout,则根据电荷守恒,会有正电荷在图中拐角处积累。
这样一来,累积起来的正电荷就会产生一个方向向外的电场,累积的越多则电场越强。从图中可以看出,这个电场在流入电路的部分与电流方向相反,减小了单位电荷所受的合力,而在流出电流的部分与电流方向相同,增大了单位电荷所受的合力。
根据上述的欧姆定律,我们立即知道随着电荷的累积,流入的电流会逐步减小而流出的电流会逐步变大,直到二者相等,则电荷不再累积,电流也不再变化,电路达到稳定状态。在实际的电路中,静电场几乎无处不在,其来自于在电路中积累的电荷,反馈式地调节着电路中各个部分的电流大小。
细心的读者可能注意到前文提到了“稳恒电路”的条件,事实上,即使是在交变电流的情况下,只要电路中的电流变化不是很快(交流电路的(角)频率ω足够低:ω<<c/L,其中c是光速,L是电路的长度尺度),则在电流发生改变时,电荷重新分布的速度都远比它快得多。
因此在任意时刻,交变电路都可以看成是一个“瞬时的稳恒电路”,上面的所有论述仍然是成立的(电流密度的散度处处为0)。
这其实也是“电路”这一模型的适用极限:如果频率过高,则不能再用电路中诸如“电压”、“电阻”、“电容”等概念进行分析,而要使用完整的电磁场理论,将电路看成电磁介质,仔细讨论电荷和电磁场的动力学问题,这样的“电路”就成为波导了。
我们可以把这种电流变化足够缓慢的情况称之为“近稳恒电路”,它实际上就是笔者在“漫话麦克斯韦方程组”专题的第一篇文章中提到的“准静态近似”的情况(例如电容器是“电学准静态近似”,电感器是“磁学准静态近似”,而电阻器既可以看作是电学也可以看作是磁学准静态近似),在此不再赘述。
不过需要强调的一点是:在电流可以随时间改变的一般情形下,本节中提到的由电荷积累产生的“静电场”应改称之为“纵向电场”,其对电荷产生的作用力就是“静电力”。
从微观形式来看,电流的流动也遵循力的守恒,力相同,产生的力的场就抵消,就导致电流的动态平衡状态。从外电场来看,受到E的作用在平衡状态下移动,在内电场来看,由于消耗非静电力将电荷从地处拉到高处,周而复始。
作者:陈 昊 沙威 戴希
只看到了这一点,还有好多没有放出来,下面放原文,有兴趣的可以自行阅读:https://mp.weixin.qq.com/s/EyPz1nFDFOCHGkmv1i5wHg