科普驿站 第59期
科目：物理
难度：B2
讲师：咕咕叶
·电子的自旋
原子中的电子不但具有轨道角动量，而且还具有自旋角动量。这一事实可以使用经典模型进行类比——太阳系中，地球不仅具有绕太阳运动的轨道角动量，还具有自转的自旋角动量。但特别要注意的是，就像不能用轨道概念描述电子云一样，我们也不能把经典模型中小球的自旋硬套在电子上。
事实上，电子的自旋与它的质量和电荷量一样，都是一种内禀的属性，即一种固有的性质。由于这种性质具有角动量的一切特征，因此我们称之为自旋角动量，也简称自旋。
与轨道角动量一样，自旋角动量也是量子化的。
·自旋量子数
s被称为自旋量子数，和轨道量子数l不同，电子的s只能取1⁄2这一个值。电子自旋的大小为
S=√(s(s+1) ) ℏ=√3/2 ℏ
电子自旋在某一方向（如x方向）的投影为
S_x=m_s ℏ
其中m_s叫做电子的自旋磁量子数，它只取两个值
m_s=±1/2
和轨道角动量一样，自旋角动量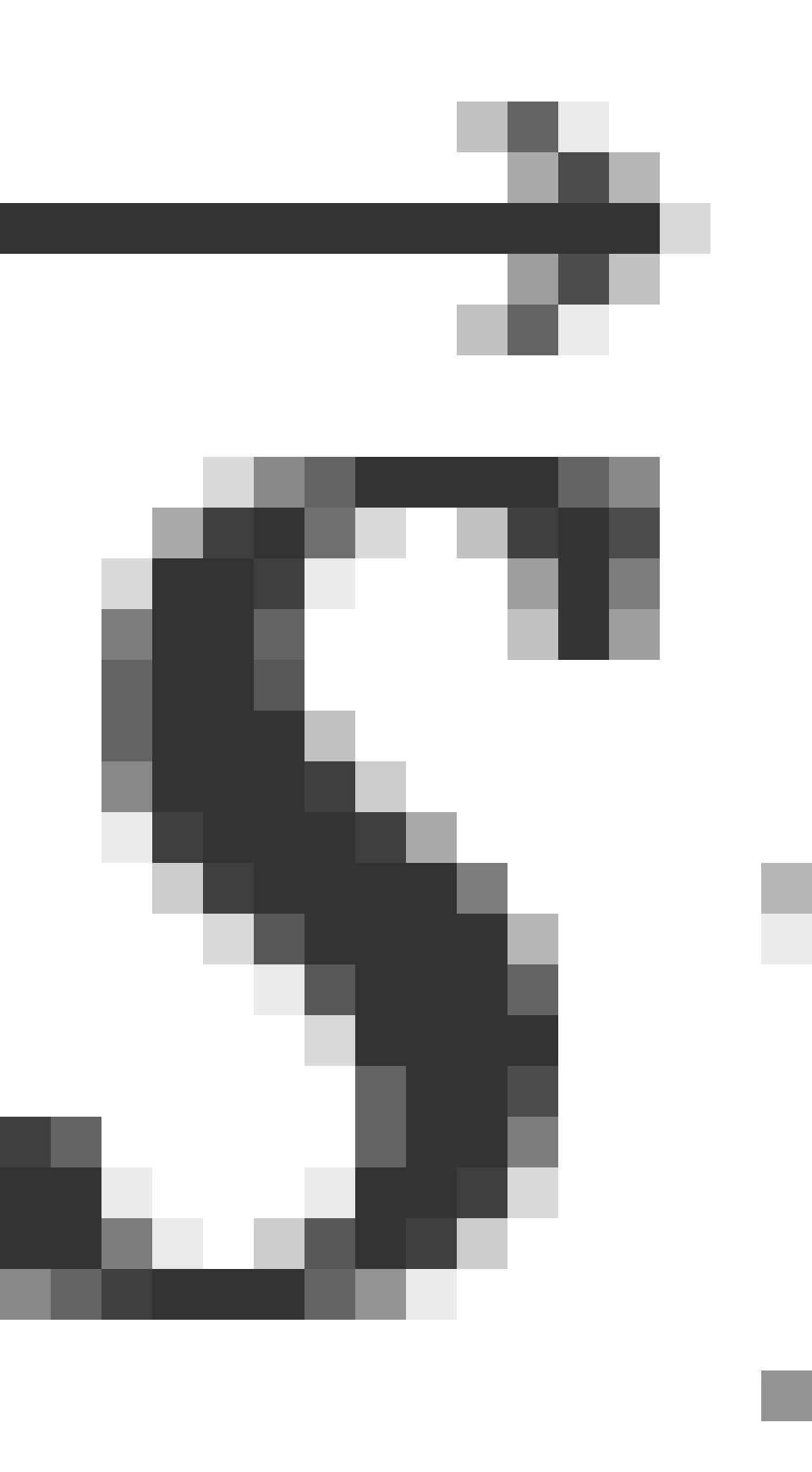
是不能测定的，只有
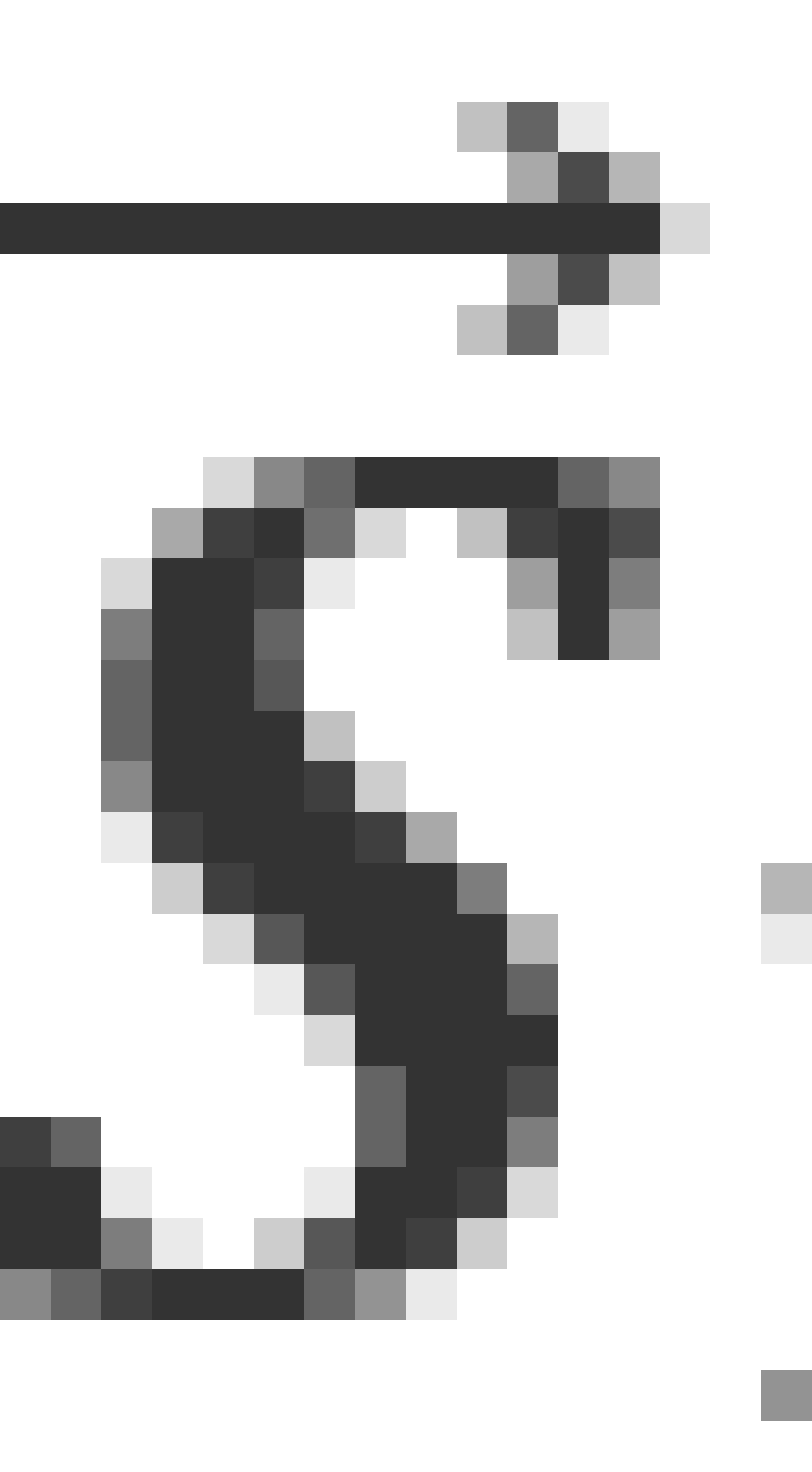沿特定方向的分量可以测定。当一个电子绕核运动时，既有轨道角动量
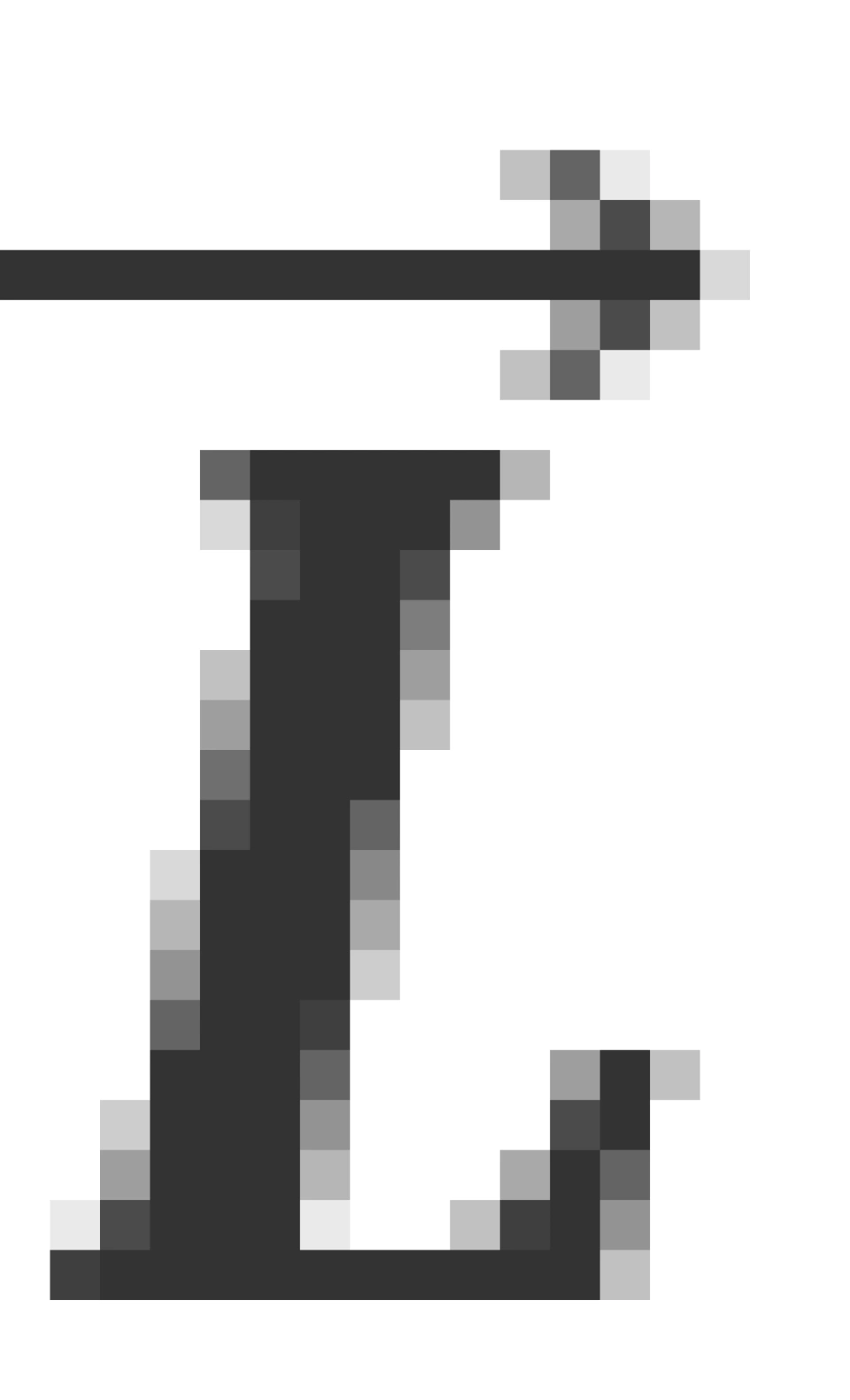，又有自旋角动量
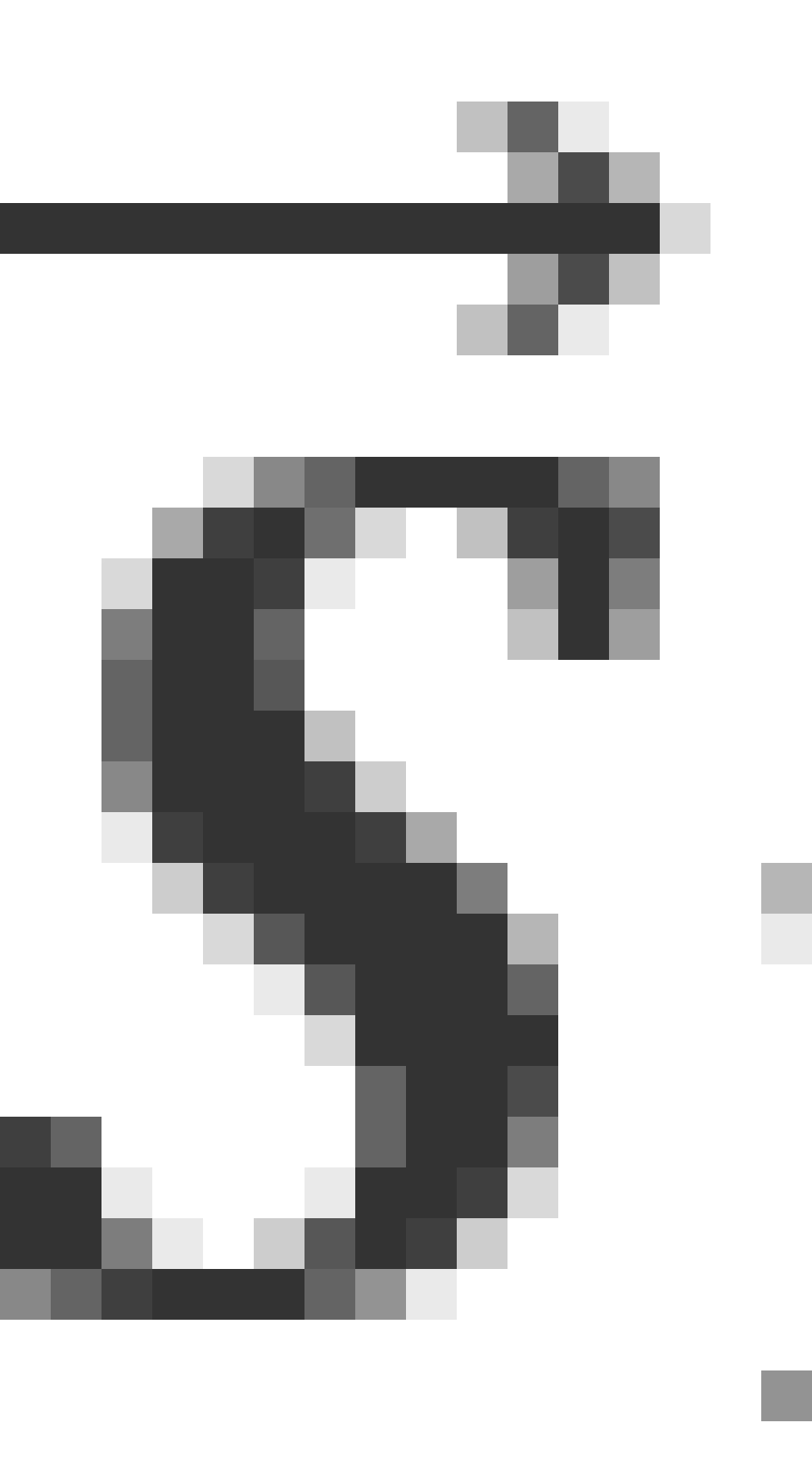。这时，电子的状态和总的角动量
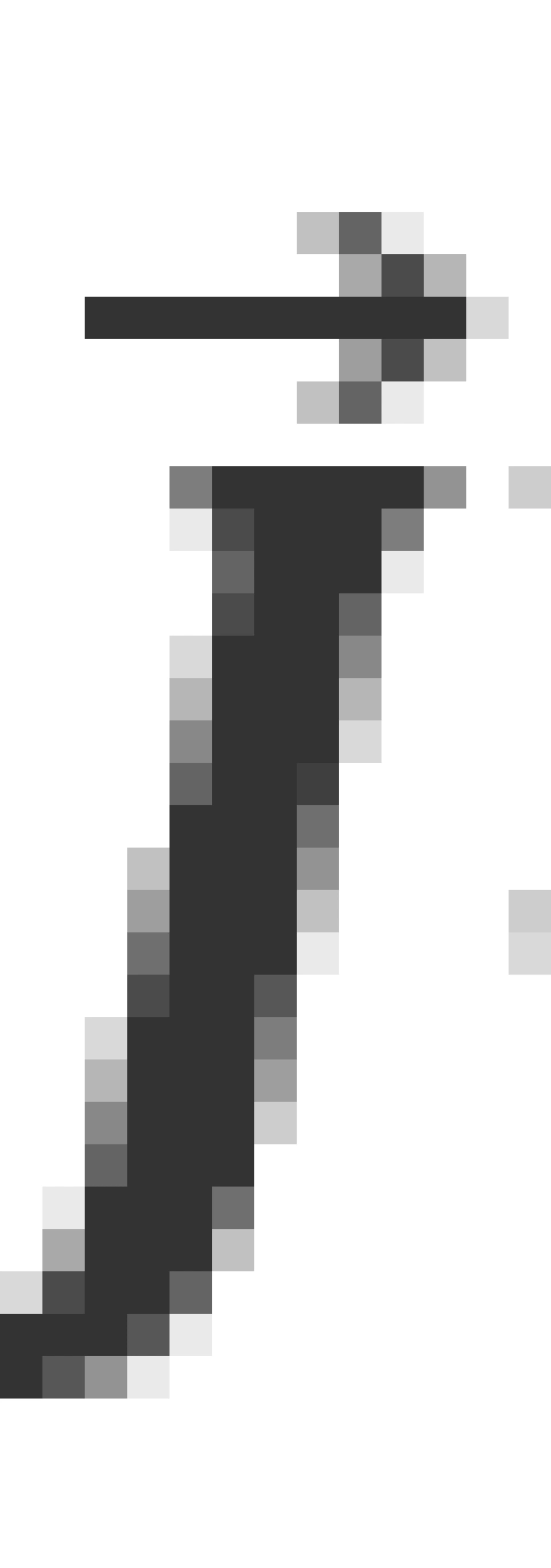有关，其中
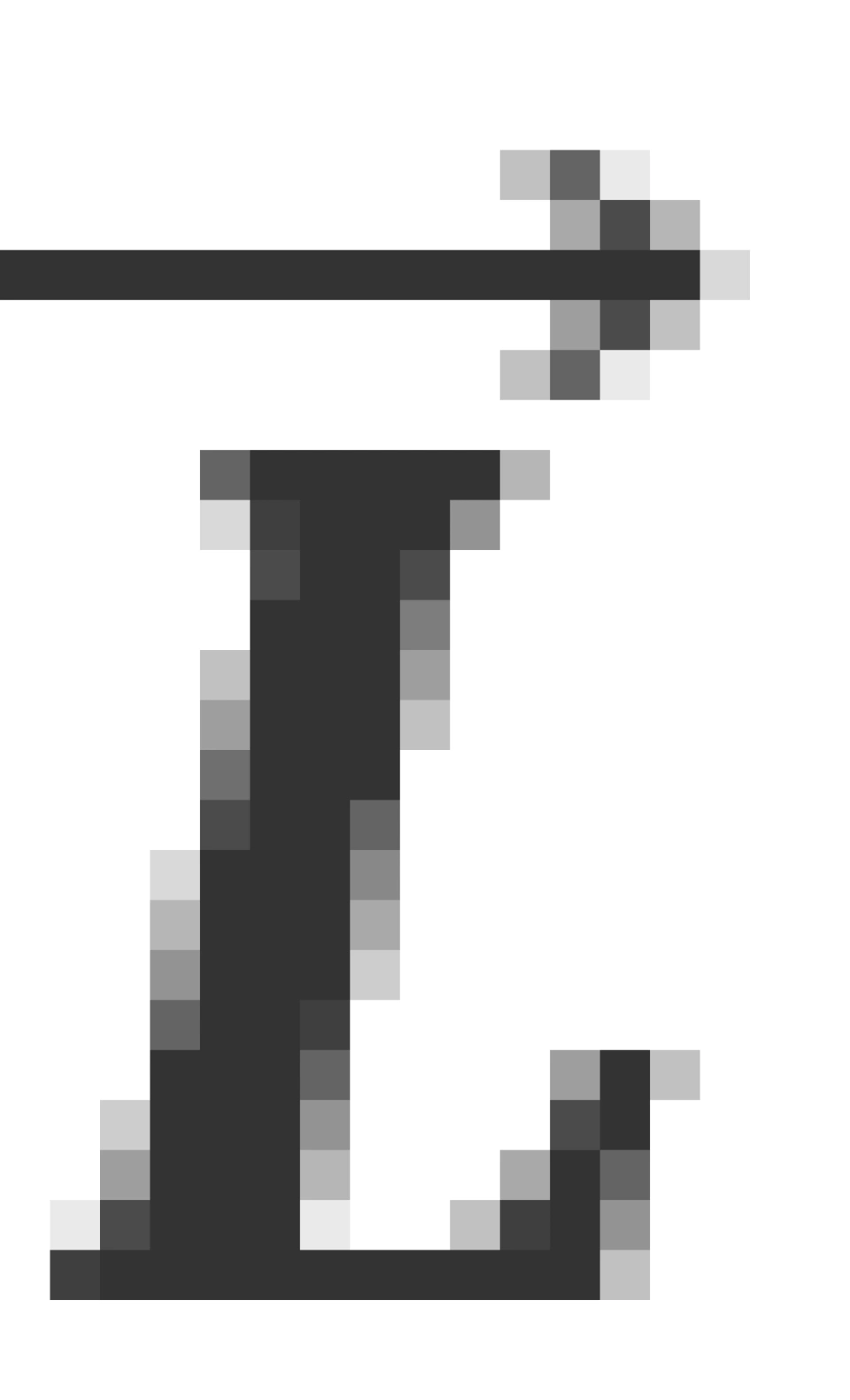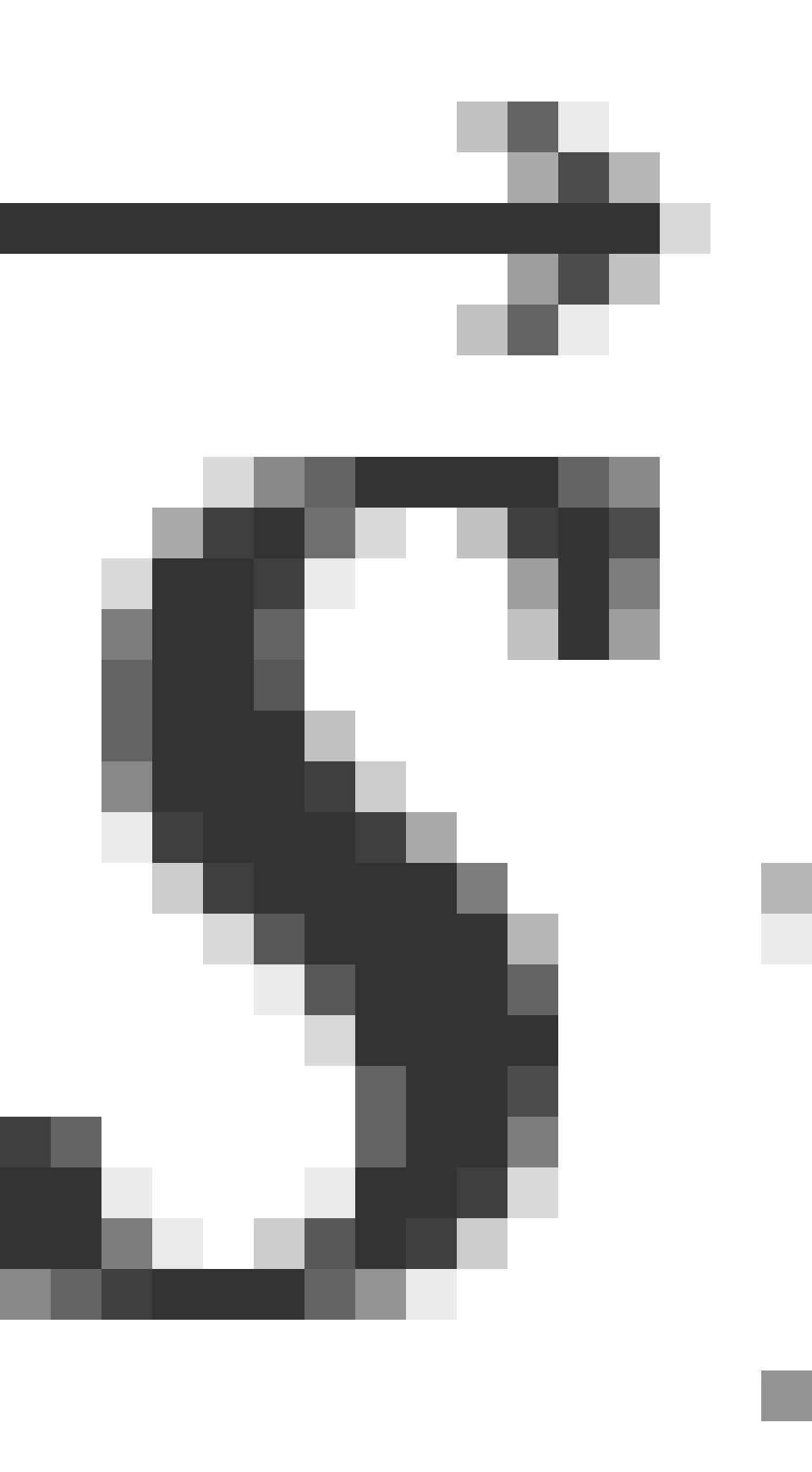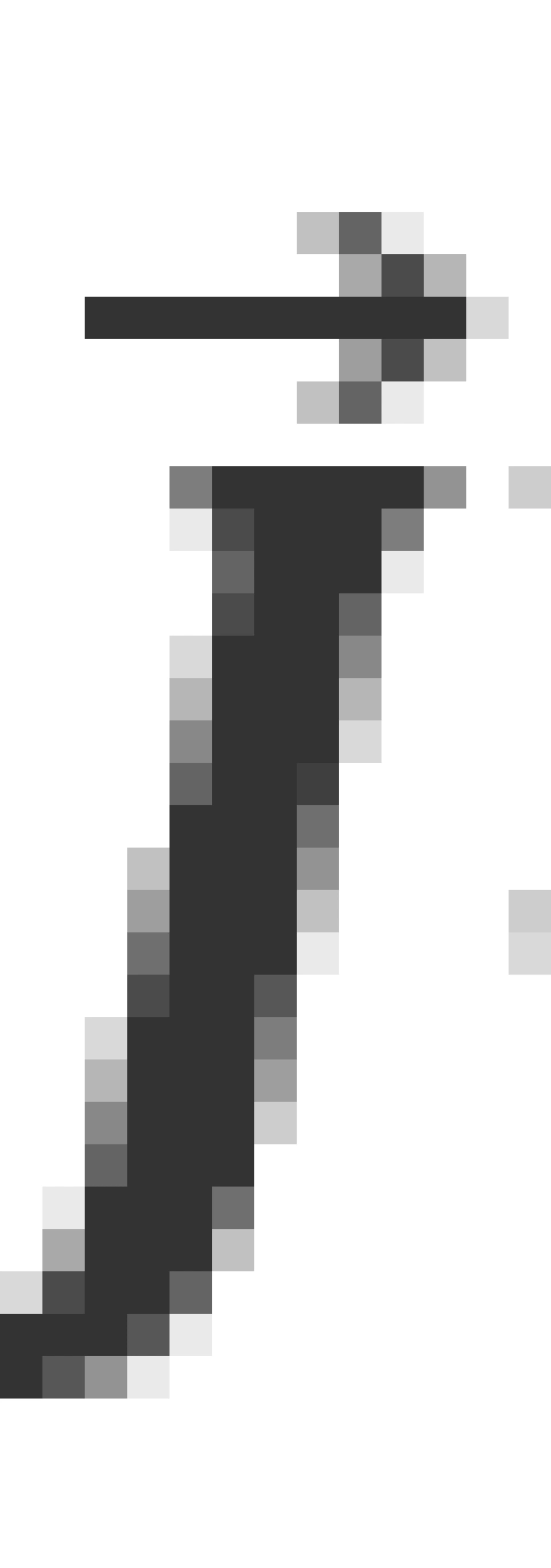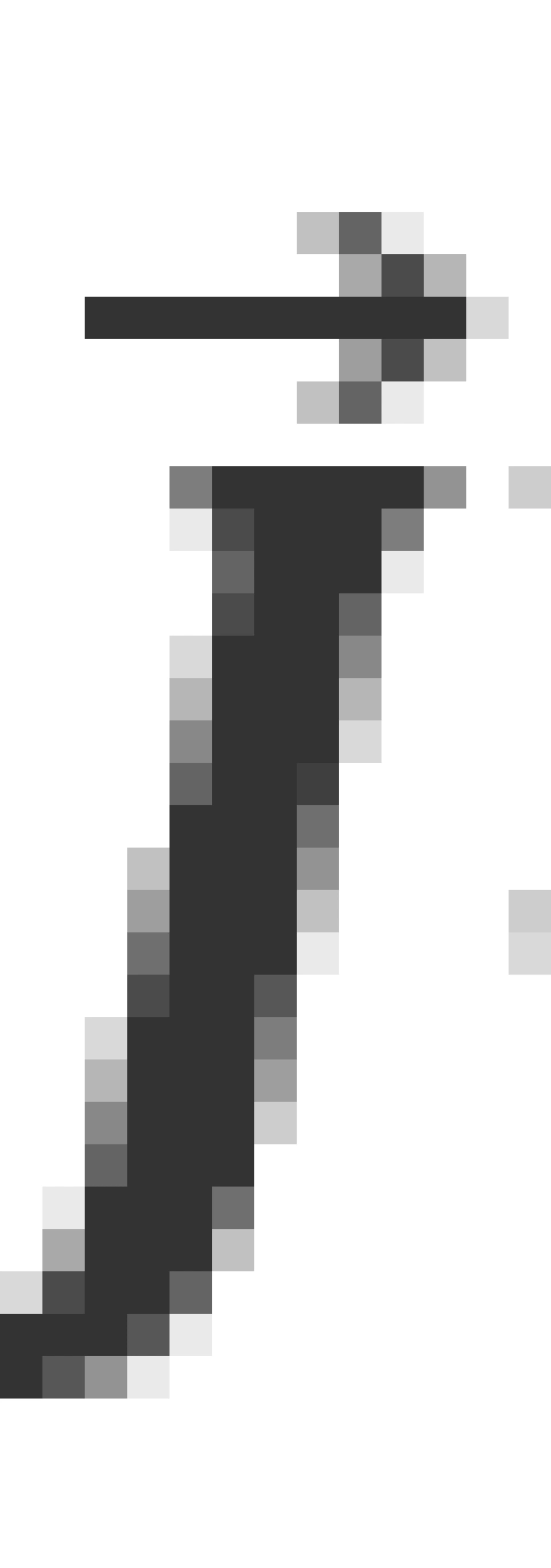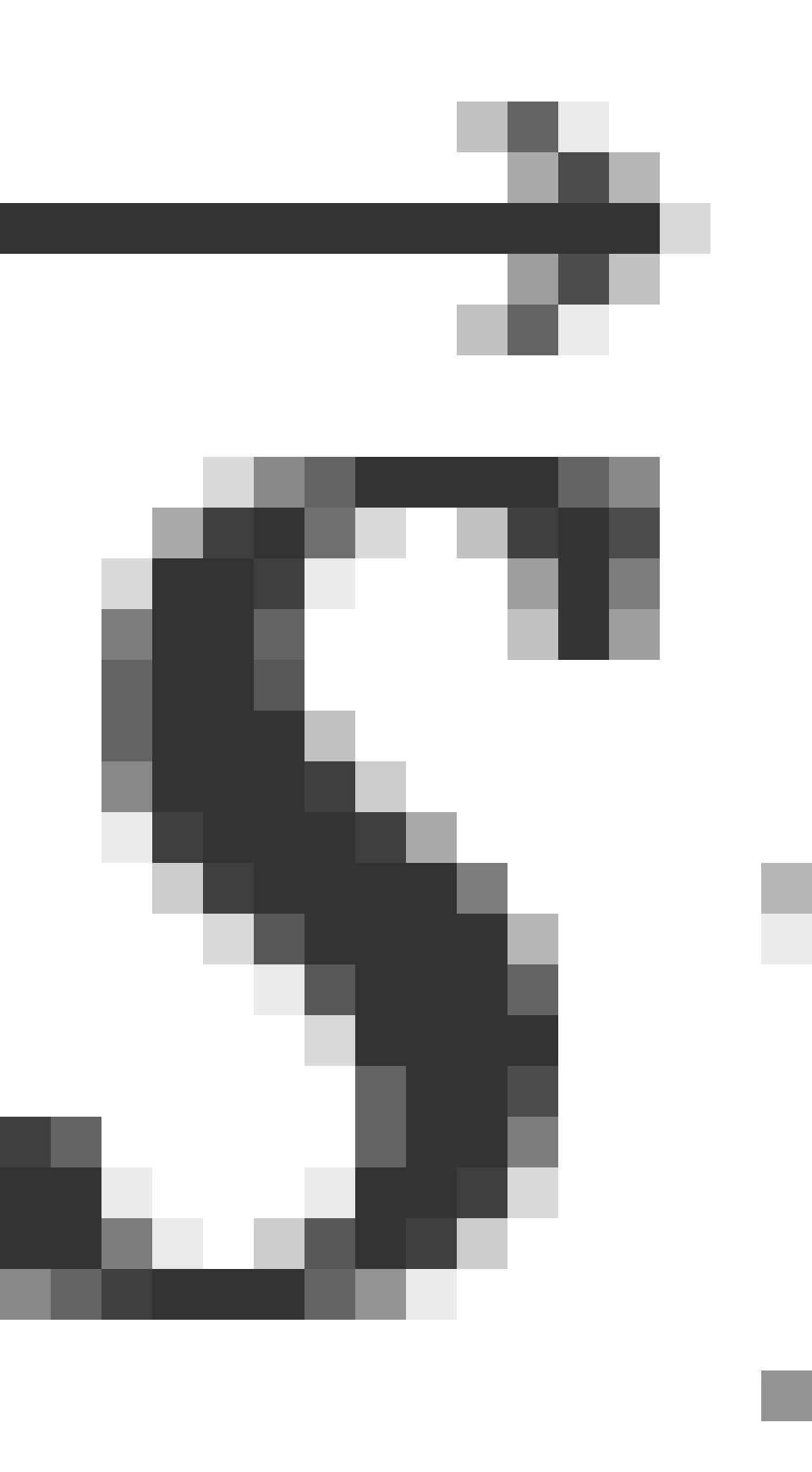由于和都是量子化的，那么必然也是量子化的，因此可以类似的将做与和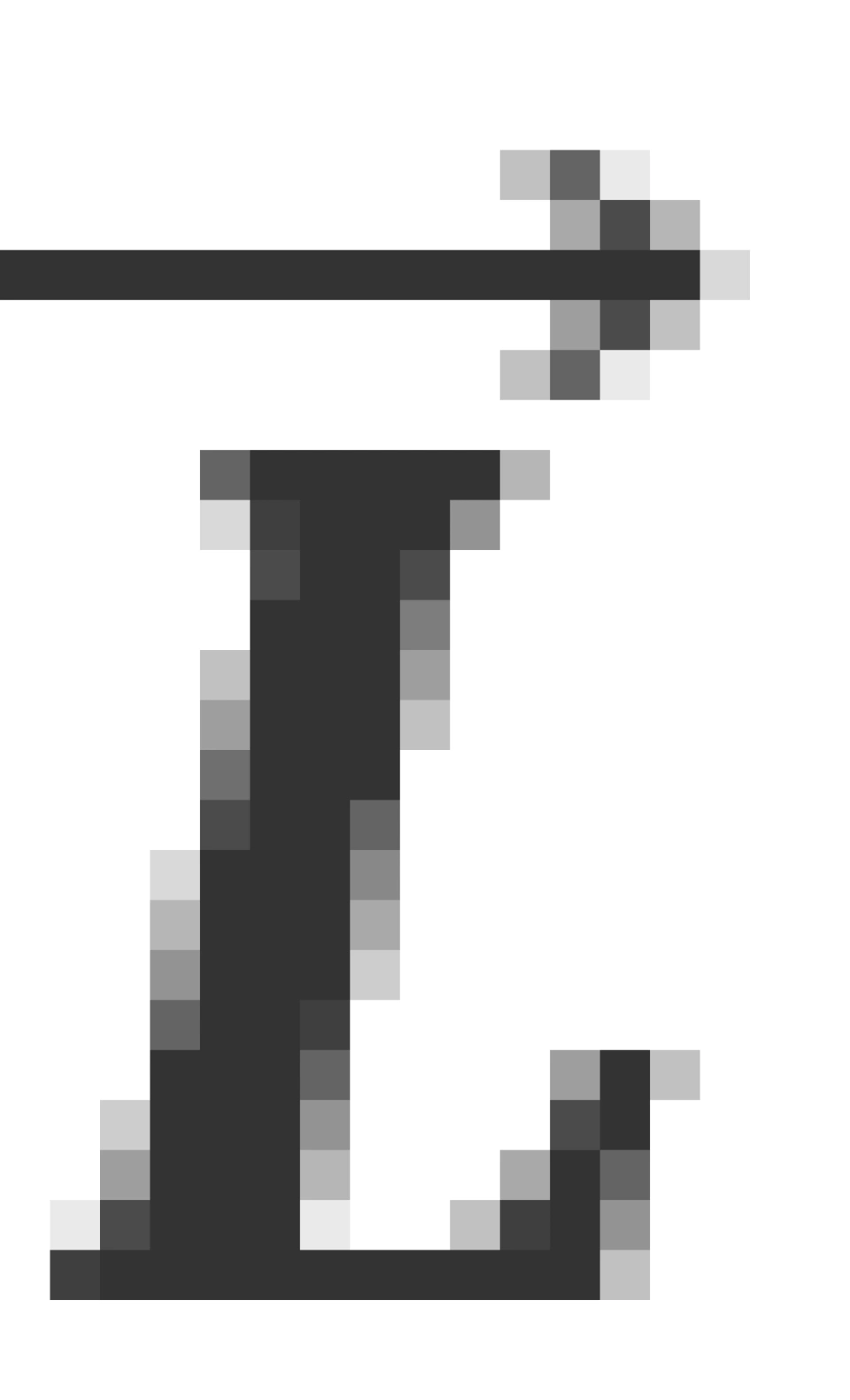同样的处理，即用j表示总角动量量子数，那么就有
J=√(j(j+1) ) ℏ
j的取值取决于l和s。以下是j取值的几种情况
其中，②的情况称为自旋和轨道角动量平行；③的情况称为自旋和轨道角动量反平行。
全同性原理
每一种微观的粒子，同种粒子的各个个体的质量、电荷、自旋等内禀性质都是完全相同的，因而是不能区分的。我们把这样性质完全相同的粒子称为全同粒子。在性质相同这一点上，经典理论和量子理论达成了一致，但二者还是具有一定区别的。
·经典理论认为同种粒子虽然不能区分，但它们在运动中可以识别。
举一个例子，粒子1和粒子2在碰撞前后，均有清晰的运动轨迹，因此我们可以在碰撞后分辨出哪个是碰撞前的粒子1或粒子2。
·量子力学理论中，粒子具有波动性，在运动中是不可识别的。
粒子1与粒子2的碰撞实际上是它们对应德布罗意波的波函数发生了干涉叠加。对于这种粒子的“混合”，我们无法辨别出碰撞后的粒子1和粒子2了。可以说，量子力学理论对同类的微观粒子不能区分的认识，要更加“彻底”一些。我们把这种不能区分叫做粒子的全同性原理，即全同粒子的不可分辨性。
·玻色子与费米子
量子力学理论的不可分辨性产生了重要的结果。对于含有不止一个粒子的系统，其波函数必须考虑这种全同性。下面我们以一维势阱中的两个粒子为例进行讨论。
以x_1和x_2分别表示两个粒子的空间坐标，那它们的空间波函数应当是两个空间坐标的函数
ψ=ψ(x_1,x_2 )
粒子1出现在dx_1区间内和粒子2出现在dx_2区间内的概率为
P_(x_1,x_2 )=|ψ(x_1,x_2 )|^2 dx_1 dx_2
现在如果将两粒子交换，即粒子1出现在dx_2区间，粒子2出现在dx_1区间的概率为
P_(x_2,x_1 )=|ψ(x_2,x_1 )|^2 dx_2 dx_1
由于量子理论的不可分辨性，我们不能识别哪个是粒子1，哪个是粒子2，所以上面两式表示的概率必然相等，则有
|ψ(x_1,x_2 )|^2=|ψ(x_2,x_1 )|^2
那么，两个粒子的波函数就必然满足以下约束方程
ψ(x_1,x_2 )=e^iδ ψ(x_2,x_1 )
其中δ为一待定相位。为了确定该相位，把两粒子的坐标再次交换。通过第二次坐标交换，波函数将再多出一个相位δ。同时考虑到两次交换后粒子的坐标波函数将完全还原，即
ψ(x_1,x_2 ) e^iδ ψ(x_2,x_1 )=e^2iδ ψ(x_1,x_2 )
此式成立的条件为，δ为π的整数倍。也可以说，粒子的波函数必须满足以下两个条件的其中一个
ψ(x_1,x_2 )=ψ(x_2,x_1 ) ①
或是
ψ(x_1,x_2 )= -ψ(x_2,x_1 ) ②
满足条件①的波函数被称为是对称的，波函数为对称的粒子叫做玻色子；满足条件②的波函数被称为是反对称的，波函数为反对称的粒子称为费米子。
更一般的理论与实验证明，自旋量子数为半整数，如1⁄2，3⁄2，的粒子，包括电子、质子、中子等是费米子；自旋量子数是整数的粒子，如氘核、氢原子、α粒子、光子等是玻色子。
·泡利不相容原理
通俗来讲，泡利不相容原理的内容是：不能有任何两个费米子同时处于完全相同的状态。
要完整描述粒子的状态，它的波函数除了包含空间波函数外，还需要包含自旋波函数，我们用X表示。因此在对换坐标x_1和x_2时，还应对换自旋磁量子数m_s。
我们以电子为例。电子的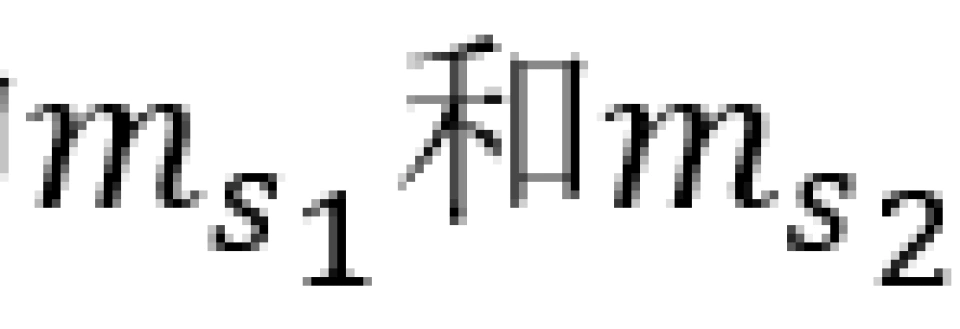
都只能取值±1⁄2，我们下面就用“+”和“-”分别表示“自旋上”和“自旋下”的波函数X_+和X_-。因此，粒子的总波函数反对称可表示为
进一步说明这种反对称性的影响，我们假设在一维势阱中的两个电子的相互影响可忽略，它们的状态只由势阱的势函数决定。当两个电子处于同一轨道时，它们的轨道波函数ψ_0 (x)是相同的。那么每个电子的完整波函数就表示为
ψ_0 (x) X_+ 或是 ψ_0 (x) X_-
由于两个电子分别出现在x_1和x_2处的概率是二者概率的积，那么系统的完整波函数为
或是几个这样形式的积的线性叠加。考虑到反对称的要求，唯一的可能叠加式是
观察此式可得，粒子1和粒子2的自旋是相反的。也就是说，在轨道波函数相同的情况下，电子的自旋必须是相反的，一个向上，一个向下。
由此推广可以得到一个重要结论：对于任何费米子系统，如果描述状态的量子数包括自旋磁量子数，那么这个系统的任何一个确定的状态内不可能有多于一个的同种粒子存在。这就是泡利不相容原理，它是1925年泡利在研究原子中电子的排布时提出的。
量子隧穿效应
在微观世界中，粒子的行为变得“反常”，量子隧穿效应就是一种十分反直觉的效应。在研究隧穿效应之前，我们先来基本了解一下简化的研究方法。
·理想模型——势阱
首先，我们讨论粒子在一种简单的外力场中做一维运动的情形。
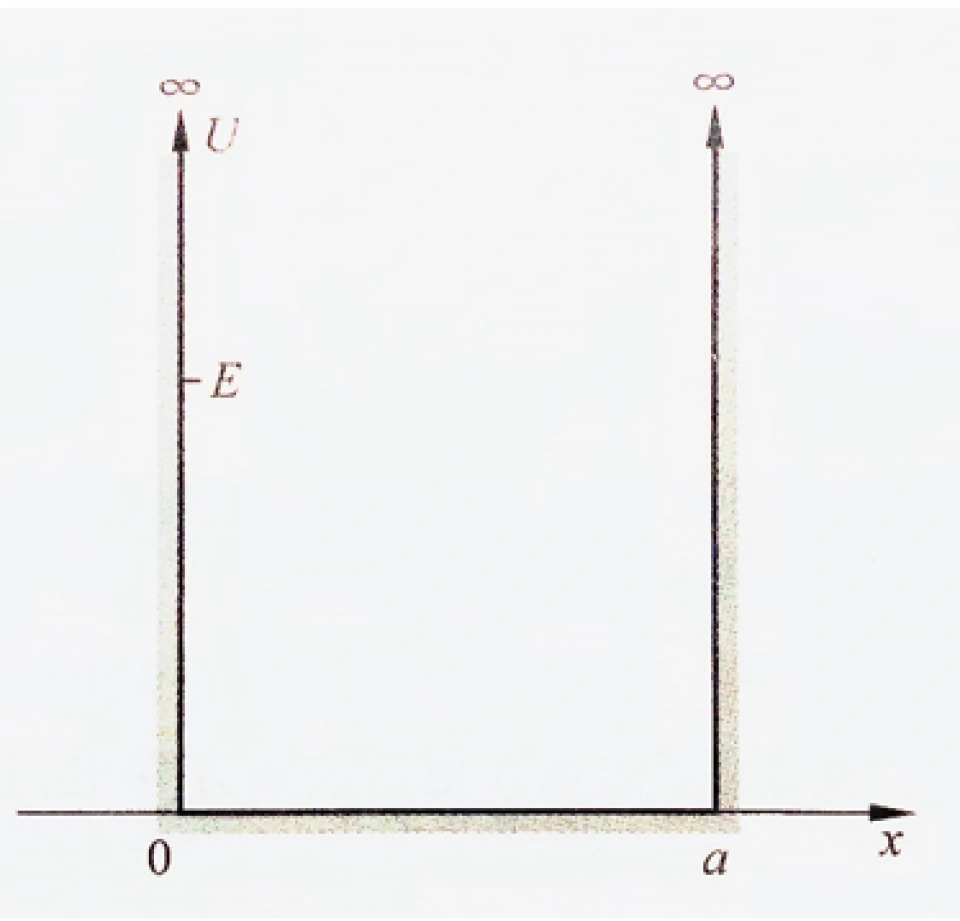
如图所示，给定一个外力场，定义它的势能函数为
可以看到，这条势能曲线像一口井，所以叫这样的势能分布为势阱。这里的井深无限，所以叫无限深方势阱。在势阱内，势能是常量，所以粒子不受力而做自由运动。而在边界x=0与x=a处，势能为无穷大，所以粒子将受到一个无穷大指向内的力。因此，粒子的位置将被束缚在势阱内而不会逃离这个范围。此时粒子的状态称为束缚态。
势阱模型是一种简单的理论模型。实际运用中，我们可以将其运用到电子在金属的运动中。金属块内部的电子可以在一定程度上做自由运动，但基本不会逃离金属块。这种情况下，就可以近似认为电子处于以金属块表面为边界的无限深方势阱中，外力场就是金属原子中的电磁场。
为研究粒子的运动，我们使用定态薛定谔方程
-ℏ^2/2m (∂^2 ψ)/(∂x^2 )+Uψ=Eψ
在势阱外，由于U=∞，所以必须有
ψ=0，x<0，x>a
在边界处粒子的波函数为0，说明粒子不可能到达势阱外部。
在势阱内部，由于U=0，所以可将薛定谔方程写成以下形式
(∂^2 ψ)/(∂x^2 )=-2mE/ℏ^2 ψ=-k^2 ψ, k=√2mE/ℏ
先来看简谐运动的微分方程
F=ma=m (d^2 x)/(dt^2 )=-mω^2 x=-kx
a=(d^2 x)/(dt^2 )=-k/m x
通过观察可以发现，薛定谔方程在这里的形式与简谐运动微分方程的形式相同，那么它的解一定取以下形式
ψ=Asin(kx+φ), 0≤x≤a
由于这个解在区域内是单值、有限且连续的，而整个波函数在x=0和x=a处是连续的，必须有
Asinφ=0, x=0
Asin(ka+φ)=0, x=a
因此可以得到，ka=nπ，n取正整数。于是将结果代入原方程的解可得
ψ=Asin nπ/a x, n=1,2,3,…
由于粒子的波函数是概率波，那么它应当满足归一化条件，即粒子在空间各处的概率总和应当为1。根据前面所说的粒子在空间某处被发现的概率即为波函数在此处振幅的平方，可以对波函数分区积分
于是，便可以得到粒子的在无限深方势阱中的波函数为
ψ_n=√(2/a) sin nπ/a x, n=1,2,3,…
其中n取某个正整数，表示了粒子相应的定态波函数。同时，还可以据此求出粒子相应的能量为
E_n=(π^2 ℏ^2)/(2ma^2 ) n^2, n=1,2,3,…
由于式中的n只能取整数值，这样，根据标准条件的要求，由薛定谔方程就自然得出：束缚在势阱内的粒子的能量只能取离散的值，能量是量子化的。每一个能量值对应一个能级。这些能量值被称为能量本征值，而n就是量子数。
再将以上求得粒子的定态波函数代入含时波函数，就可以得到粒子的全部波函数了
Ψ_n=ψ_n exp((-2πiE_n t)⁄h)
这里求得的波函数叫做能量本征波函数。每个本征波函数所描述的粒子的状态称为粒子的能量本征态，其中能量最低的态叫做基态，其他叫做激发态。
接下来根据能量-动量关系可以得到，粒子德布罗意波的波长也是量子化的，它只能是势阱宽度两倍的整数分之一。因此可以说，无限深方势阱中粒子的每一个能量本征态，都对应于德布罗意波一个特定波长的驻波。
能量-动量关系，即
，德布罗意波长为λ=h/p_n 。
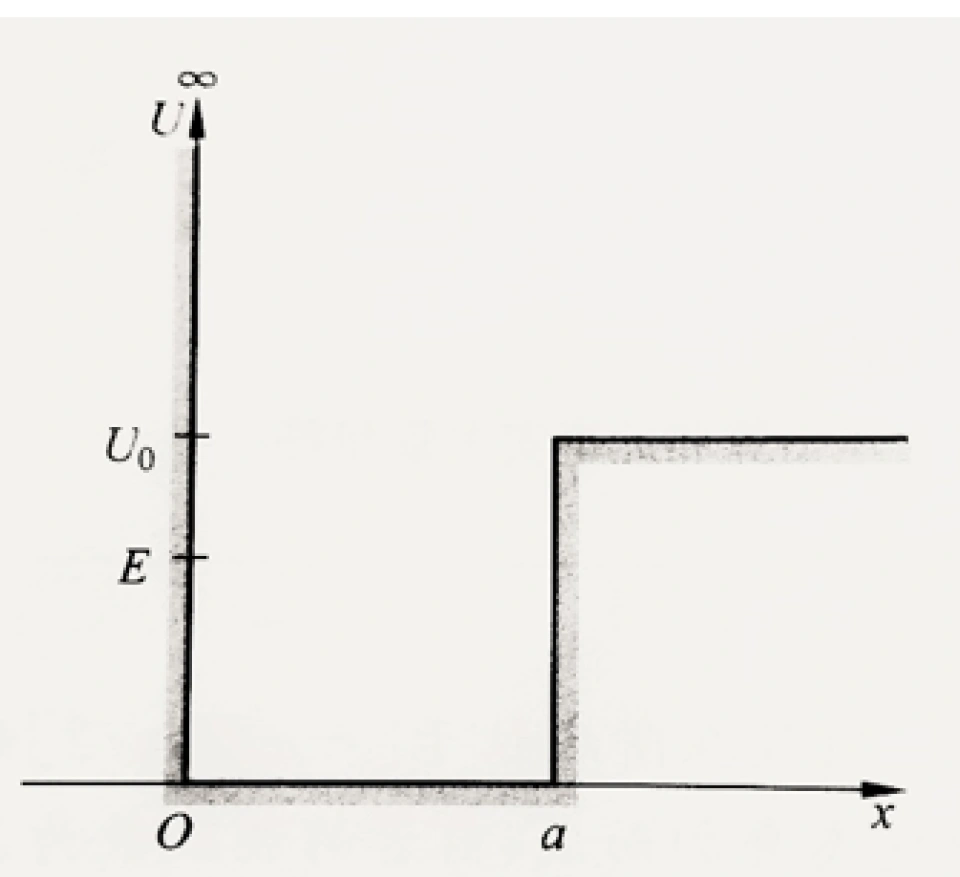
通过上述讨论，我们已经基本了解了如何求解粒子在势阱中的波函数。但在现实中，往往不会出现如此理想化的情形，势阱总不是“无限深”的。因此，我们继续改进模型，下面研究如图“半无限深方势阱”中的粒子。
如图所示，给定一个外力场的势能函数为
和刚才的分析相同，在势阱的内部，粒子的波函数一样取谐振形式的解，即
ψ=Asin(kx+φ)
在x>a的区域内，粒子的定态薛定谔方程可以写成以下形式
(∂^2 ψ)/(∂x^2 )=2m/ℏ^2 (U_0-E)ψ=〖k'〗^2 ψ
这是一个二阶常系数线性微分方程，它的通解应为
ψ=Ce^(-k'x)+De^k'x
其中C,D为常数。为了满足当x趋向正无穷时，波函数有限的条件，必须使D=0。同时又需满足此波函数在x=a处连续，则可得出约束方程
Asin(ka+φ)=Ce^(-k'a)
同时，由于波函数在x=a处的一阶导数也必须连续，因此对上式两边求导可得
kAcos(ka+φ)=-k'Ce^(-k'a)
观察以上约束方程，可以得到，对于束缚在势阱内的粒子，其能量也是量子化的，但其能量本征值的数学表达式较复杂，以下就不做讨论了。此处着重指出，由上式可得，在x>a而势能有限的区域内，粒子出现的概率不再为0，这意味着粒子在运动中有可能到达这一区域，而概率随x的增大按指数规律减小。
有趣的是，在此处出现了一个十分反直觉的现象——在粒子所具有的能量小于外力场的势能时，粒子也可以进入到相应区域，这是与经典力学不同的。
在经典力学中，粒子只能在势阱内运动，不可能进入到其能量小于势能的区域——就像一个人想要越过一堵墙，首先得获得至少相当于与墙最高处相等的重力势能。但根据上面的计算，我们发现粒子在势能大于总能量处的位置，粒子出现的概率仍然不为0，这意味着粒子的动能可以是负值！这种现象是可以用不确定性原理来理解的。
由于粒子在势能较高区域内的波函数概率密度为
|ψ|^2=C^2 e^(-2k'x)
则可以将x=1/2k'看作粒子进入该区域内的典型深度。这一距离可以认为是在此区域内发现粒子的位置不确定度Δx
∆x=1/2k'=ℏ/(2√(2m(U_0-E) ))
根据不确定性原理，粒子在这段距离内的动量不确定度为∆p
∆p≥ℏ/∆x=√(2m(U_0-E) )
则粒子进入的可能速度为∆v
∆v=∆p/m≥√(2(U_0-E)/m)
于是粒子进入的时间不确定度为∆t
∆t=∆x/∆v≤ℏ/4(U_0-E)
再由粒子的能量-时间不确定关系，可以得到粒子能量的不确定度∆E
∆E≥ℏ/2∆t≥2(U_0-E)
所以这时，粒子的总能量将为E+∆E，则其动能的不确定度∆E_k为
∆E_k=E+∆E-U_0≥U_0-E
可以看到，有趣的事情发生了。在粒子到达的区域内，它多出来的那份动能实际来自于不确定性原理赋予它的名义上的“虚动能”。这种动能是不能被观察到的，因此这和实验中观察到的能量守恒定律并不矛盾。
由于粒子可以进入势能大于其本身能量的区域，如果这以高势能区域是有限的，则粒子就是被一势垒所阻挡，粒子有可能穿透势垒在另一侧被观察到。这一现象被称作量子隧穿效应。
在实验中，这种现象是可以被观测到的。比如ɑ粒子（氦原子核）从放射性核中逸出，即ɑ衰变——ɑ粒子在核内由于核力作用，其势能是很低的。在核边界上有一个因库仑力产生的势垒。这一势垒非常高，远高于衰变过程中释放处的ɑ粒子的能量。根据实验与计算发现，这些ɑ粒子就是通过量子隧穿效应穿透库仑势垒跑出的。
再比如，储存数据的固态硬盘所用的闪存。闪存的基本存储单元是浮栅晶体管，其中的浮栅极中存储的电子就可以使用外加电压的方法，通过电子的量子隧穿效应实现输入或输出数据。
参考引源：
《大学物理学》(张三慧等),《新概念物理教程》（赵凯华等）,Feynman Lectures on Physics, Learning Notes on Quantum Mechanics(Leng Xuan),Introduction to Quantum Mechanics(David J. Griffiths),Wikipedia,bilibili等。
图片来源：
百度图片,Google Images, 《大学物理学》(张三慧等)。
【本文为耀星会的原创作品，未经允许，禁止盗用、转载、篡改文章，否则耀星会和作者将追究版权责任。】
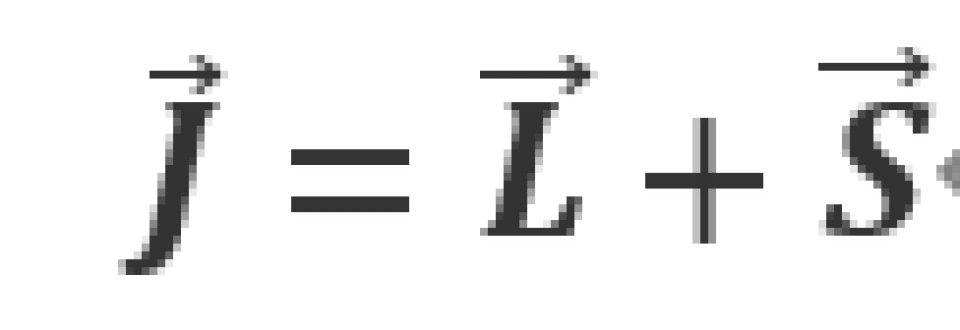
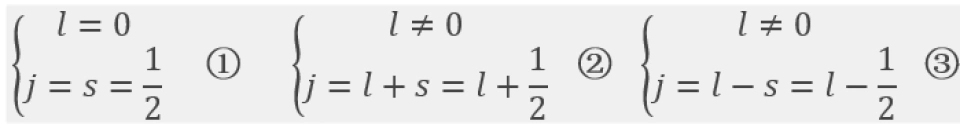
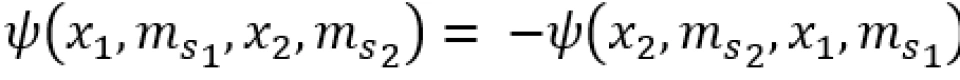
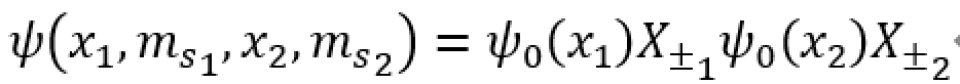
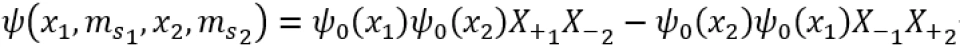
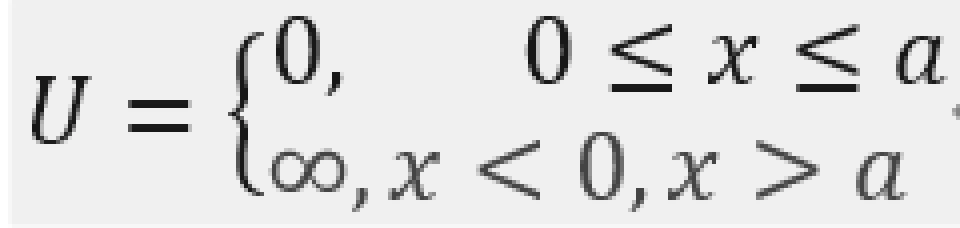
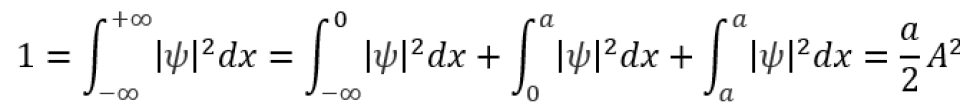
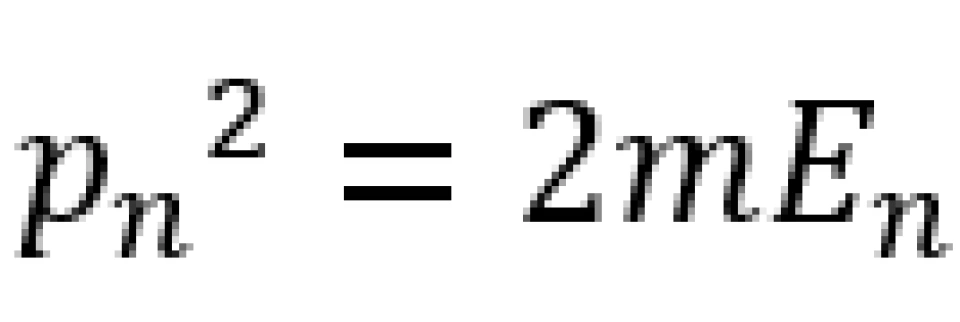
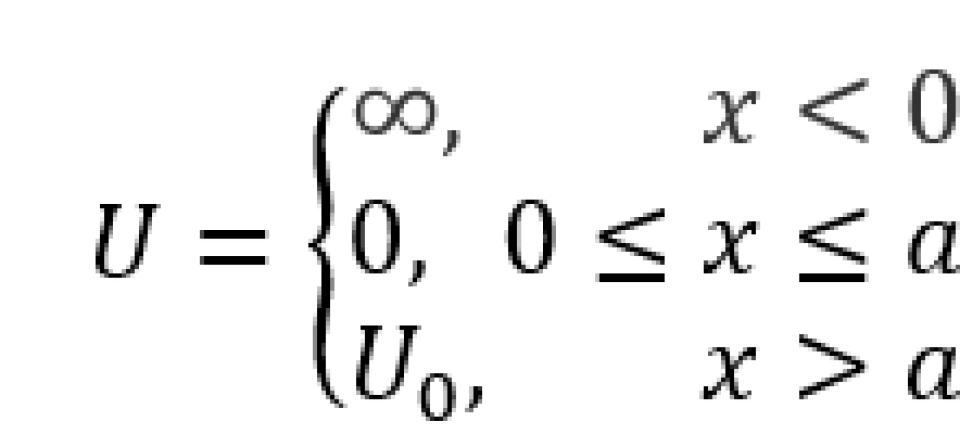
涨知识了，楼主辛苦了，谢谢楼主！