科普驿站 第59期
科目：物理
难度：B2
讲师：咕咕叶
根据卢瑟福的原子模型，我们知道，原子核由质子和中子组成，电子在原子核附近绕着原子核运动。后来，玻尔根据他的公式，给出了更加精确的原子电子轨道模型——在这个模型中，原子核周围的电子拥有特定的轨道，它们的运动被限制在了一定的区域内。根据玻尔的经验公式
其中R为里德堡常数。
此方程很好地引入了轨道量子化概念，但这终究是一个经验公式，而且它只能够解释拥有极少电子的原子，当原子拥有两个以上的电子时，它便变得十分不准确。
在薛定谔得到了它的波动方程后，事情变得明朗了起来。它更合理，或者说，从根本上解决了当时有关原子的问题，从而开始了量子力学理论的建立。下面我们来看一下具体的情景。
原子是一个三维系统，原子核中的质子带正电荷，它将产生一个电场。电子带负电荷，它在质子的库仑场中运动，处于束缚态。对于电子来说，原子核中的质子相距很近，因此可以将N个质子看作点电荷处理。它的势能为
为简化情景，我们研究
的情况，即该原子为氢原子。
观察势能函数，为电子到质子的距离。由于此势能具有球对称性，为方便求解，我们就利用定态薛定谔方程的球坐标形式，即
其中波函数是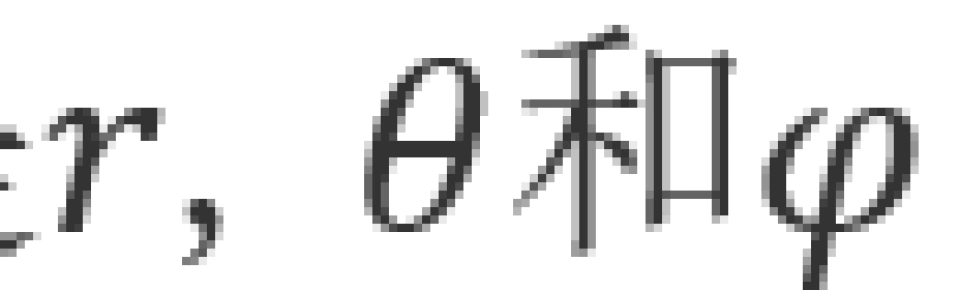
的函数，即
对这个波函数，可以用分离变量法求解
由于求解的过程和的具体形式比较复杂，我们直接来看一些结论。
由于束缚态的粒子的波函数必须满足单值、有限、连续的标准条件，根据之前所说的，求解时便自然而然得出了量子化的结果。我们得出结论，氢原子中的电子的状态由三个量子数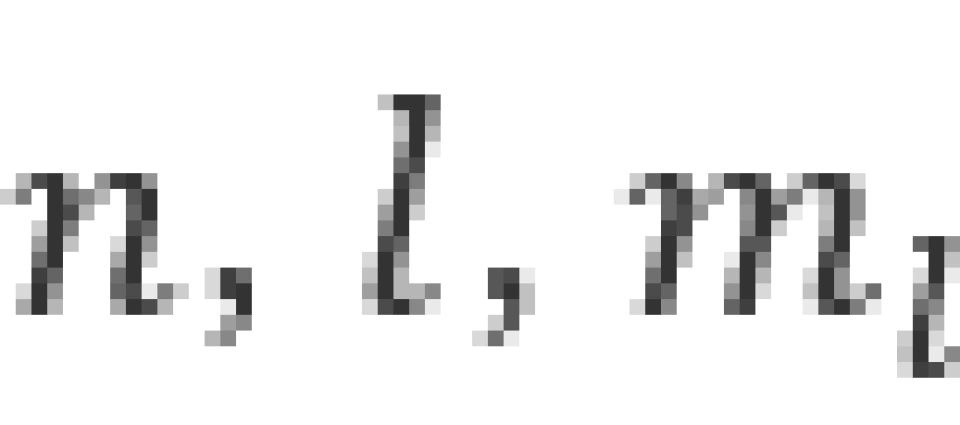
决定，下面依次进行介绍。
主量子数
n被称为主量子数，它和波函数的径向部分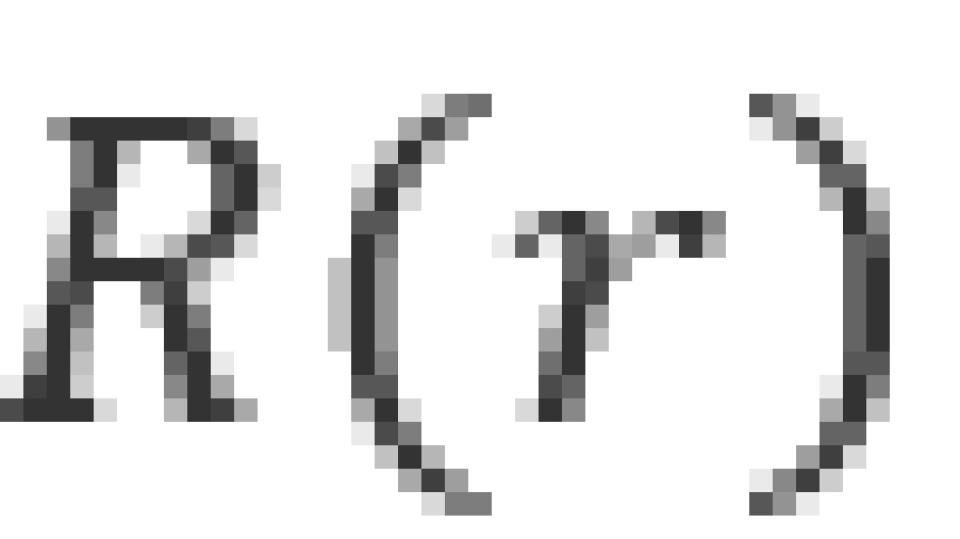
有关。它决定了电子在这个原子系统中的能量，这一能量的表达式为
其中是电子的质量。此式的数学过程这里就不赘述了。它表示氢原子的能量只能取离散的值，这就是先前玻尔所得出的轨道能量的量子化。上式也可以写成
其中
观察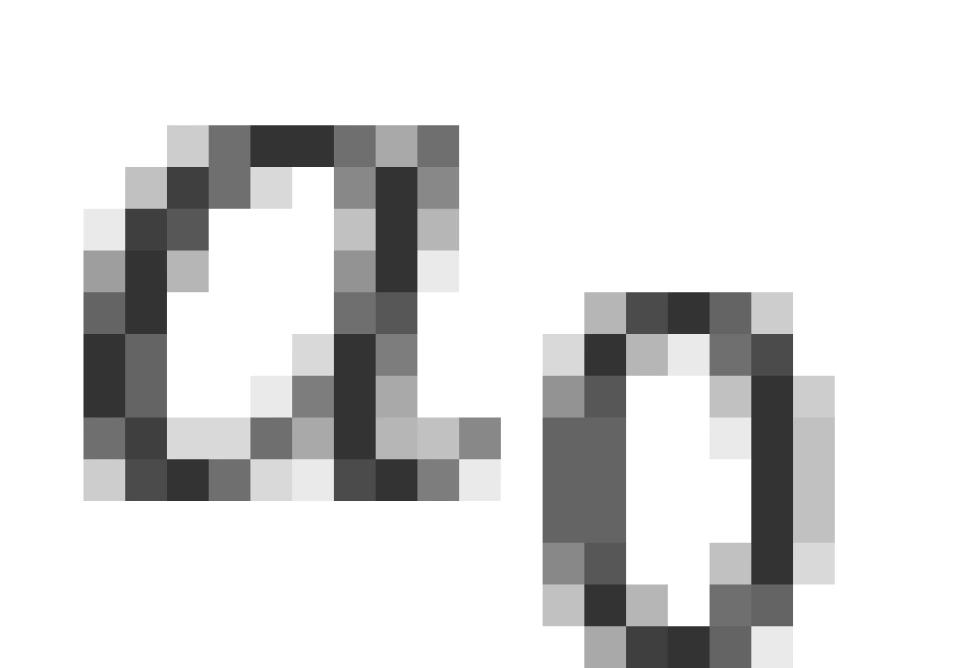
的表达式，可以发现它具有长度的量纲，那么根据原能量表达式便可以解释为：每一轨道的能量实际上都是半径为
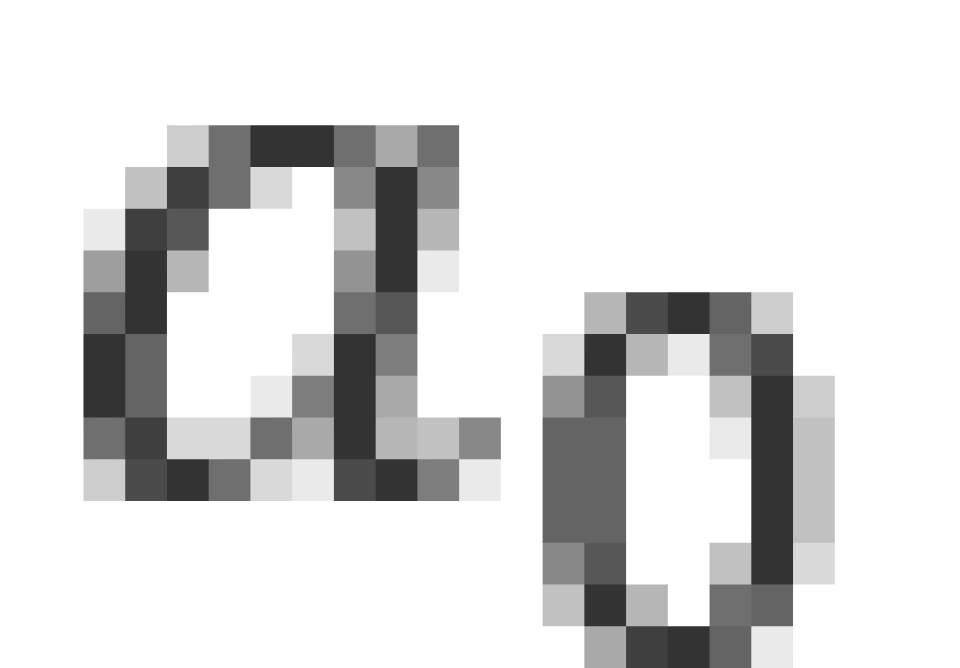的轨道的能量的常数倍，这便是玻尔得到的轨道量子化。因此，我们将
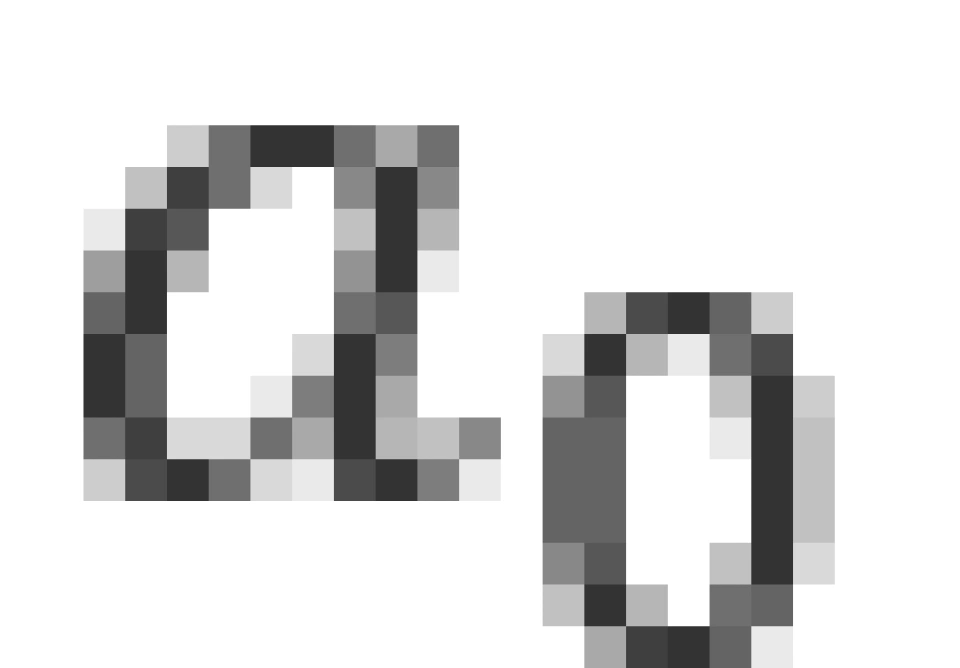命名为玻尔半径。
当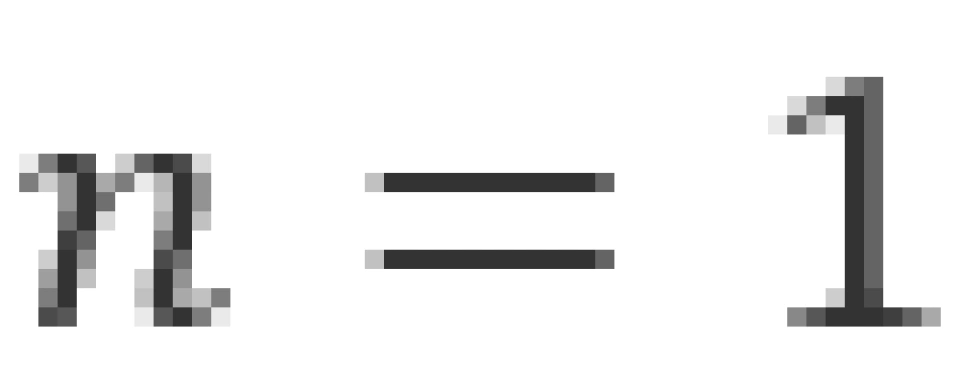
时，其势能最小，叫做基态。将以上各常量代入后，可以得到，氢原子的基态能量为
当n取不同的整数时，上式给出的每一个能量的可能取值叫做一个能级。当其势能大于零时，表示电子已经脱离原子核的吸引，氢原子已经电离。这时的电子成为了自由电子，其能量就可以具有大于零的连续值。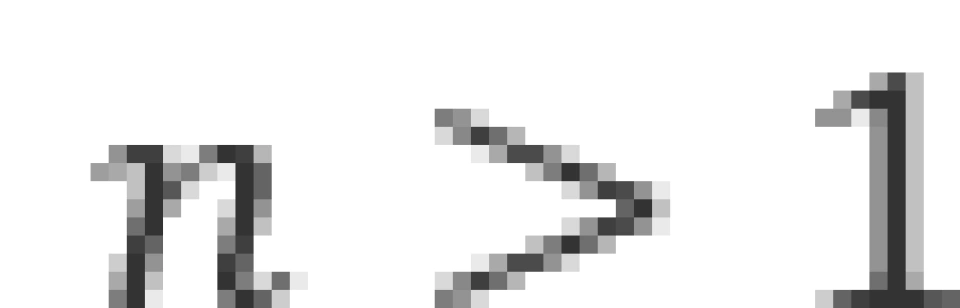
的状态统称为激发态。
通常情况下，氢原子处于能量最低的基态。当外界供给能量时，氢原子可以跃迁到某一更高能量的激发态。常见的激发方式之一是氢原子吸收一个光子而得到一份能量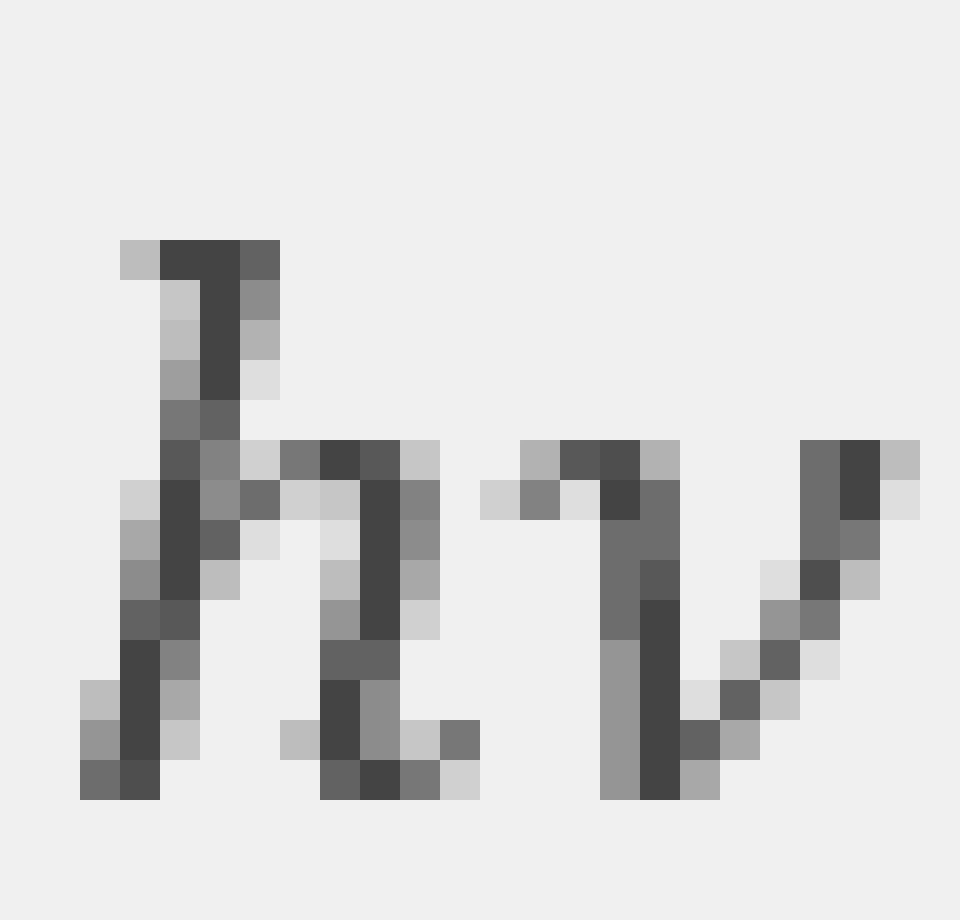
，从而跃迁到更高能量的激发态。处于激发态的原子是不稳定的，经过或长或短的时间，它会跃迁到能量较低的状态而以某种形式放出能量。
不论如何跃迁，氢原子所吸收或放出的能量必须等于相应的能级差。就吸收光子来说，必须有
式中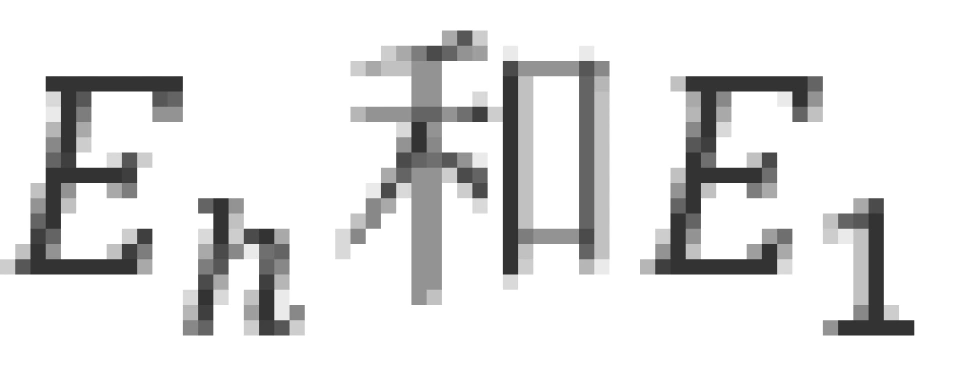
分别表示氢原子的高能级和低能级。此式叫做玻尔频率条件。
轨道量子数
l被称为轨道量子数，它和波函数的极角部分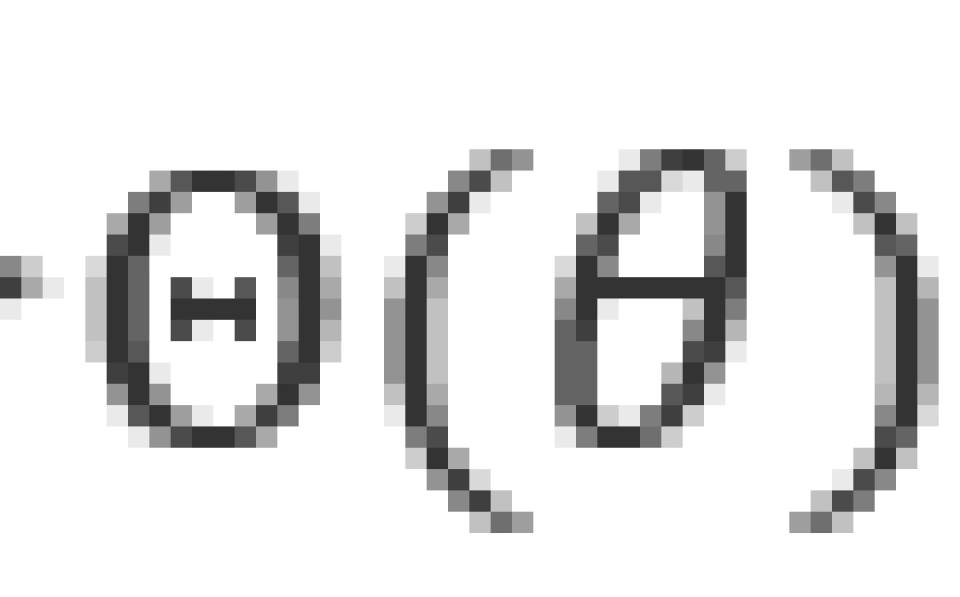
有关。它决定了电子的轨道角动量大小L。电子在核周围运动的角动量的可能取值为
这说明轨道角动量的数值也是量子化的。
轨道磁量子数
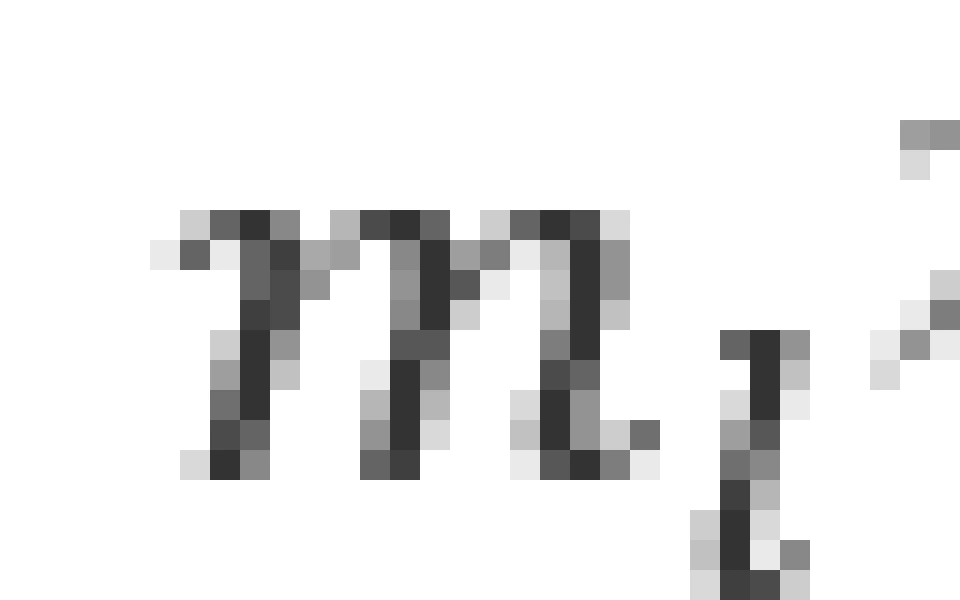被称为轨道磁量子数，也叫磁量子数，它和波函数的方位角部分
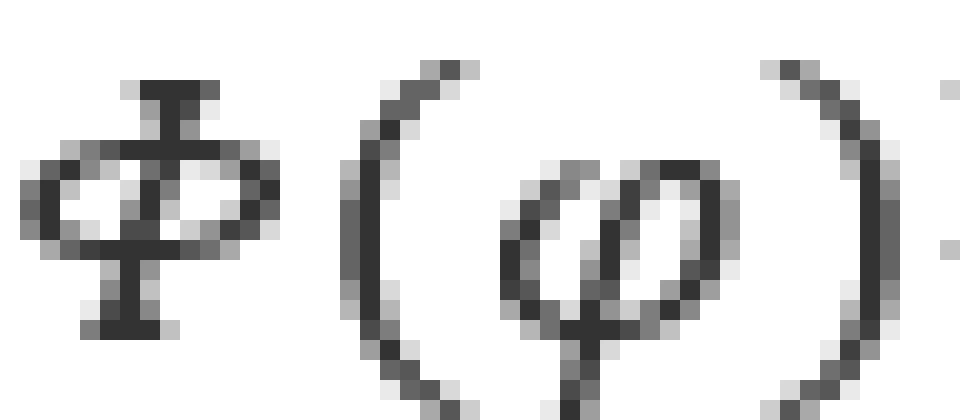有关。它决定了电子轨道角动量
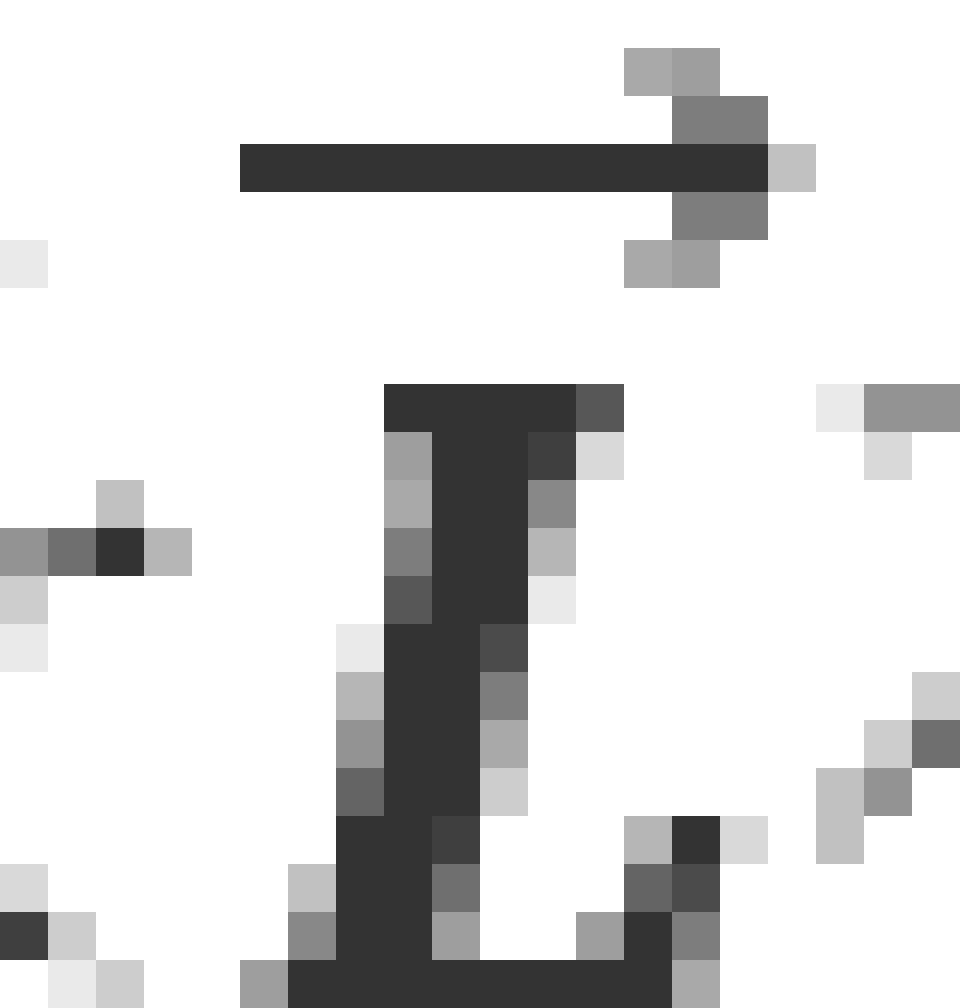在空间某一方向的投影，下面以x轴举例。
自由空间是各向同性的，也就是说，同一大小的矢量转向不同方向，其效果是等价的。那么，x轴是可以取任意方向的，这一量子数看起来似乎没有什么实际意义。但假如把原子放到磁场中，由于原子具有磁矩，那么对于电子来说附近的空间便不再是各向同性的了，这时x轴就应该选取磁场方向。此时，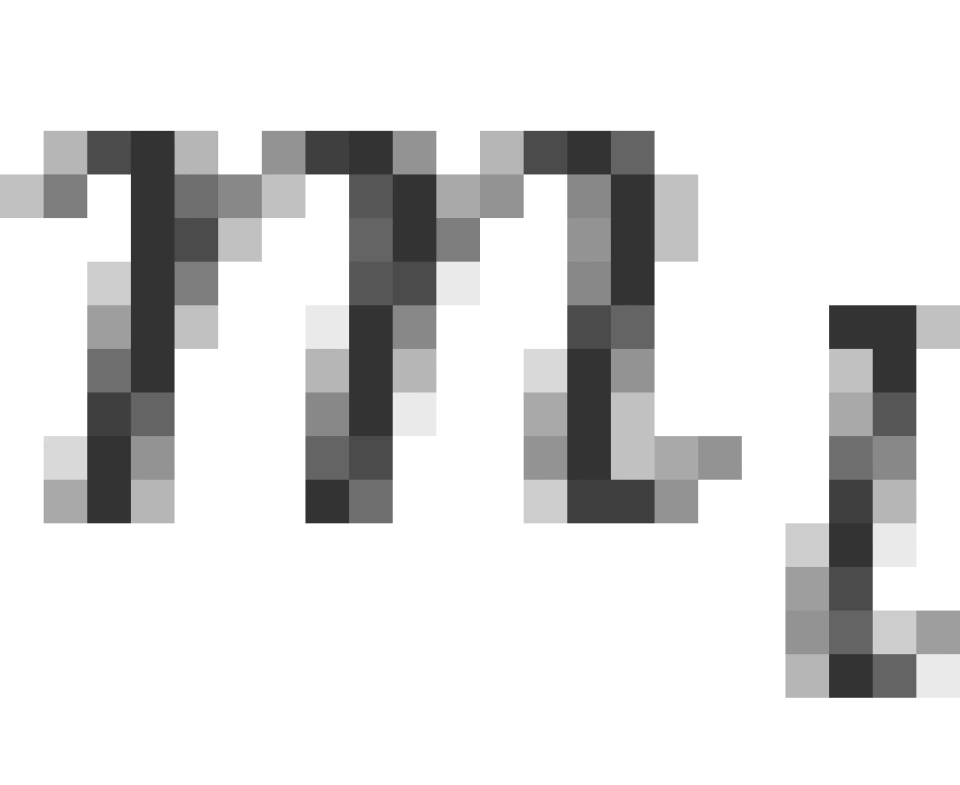
就决定了电子轨道角动量在方向上的投影，这也是为什么
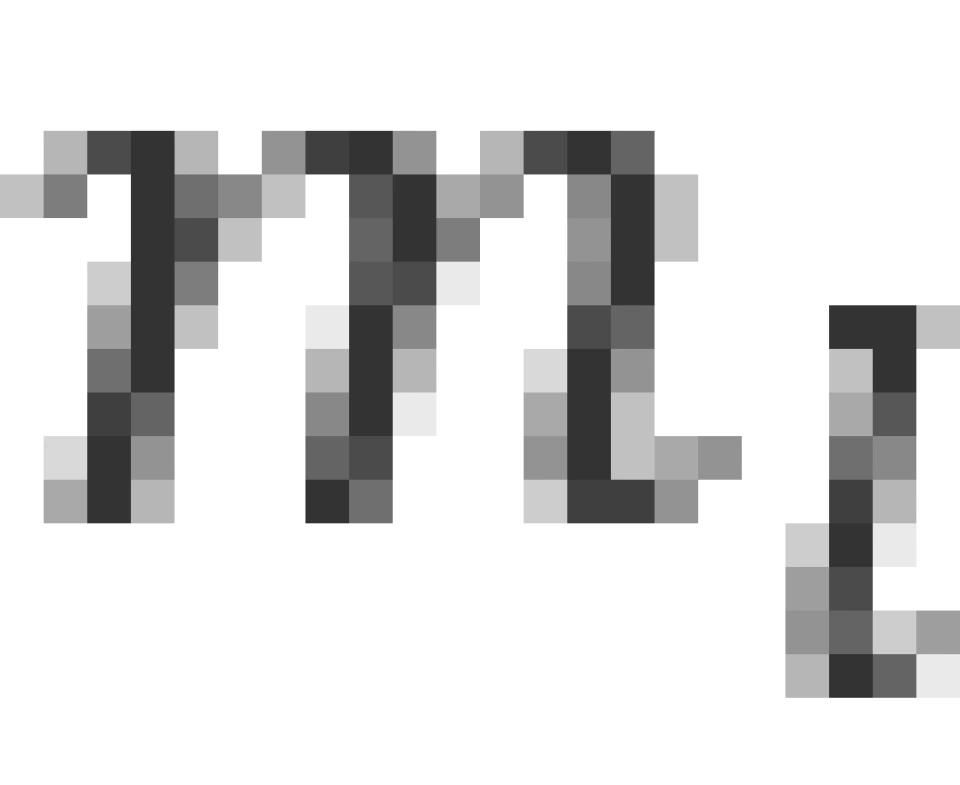叫做磁量子数的原因。
这一投影也是量子化的，由一般理论给出，这一投影的可能取值为
这也就意味着，电子的轨道角动量的指向是量子化的。因此这一现象叫做空间量子化。
有必要指出，对于确定的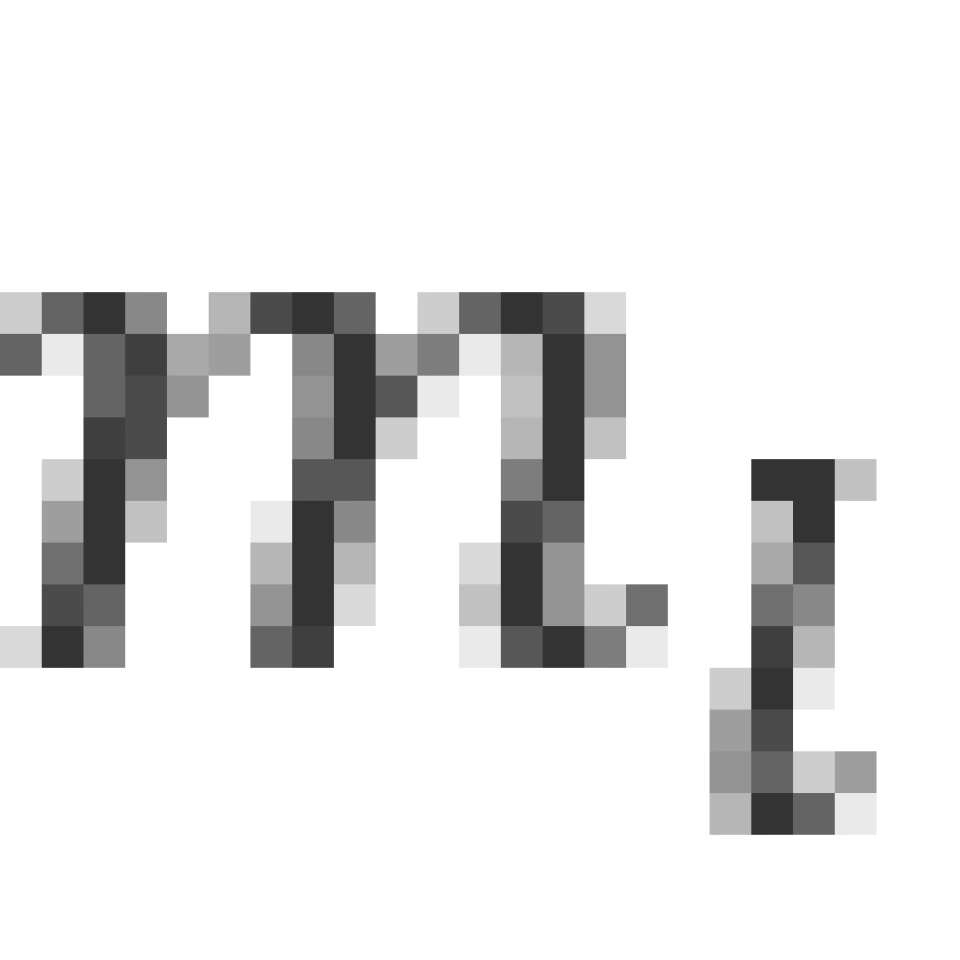
值，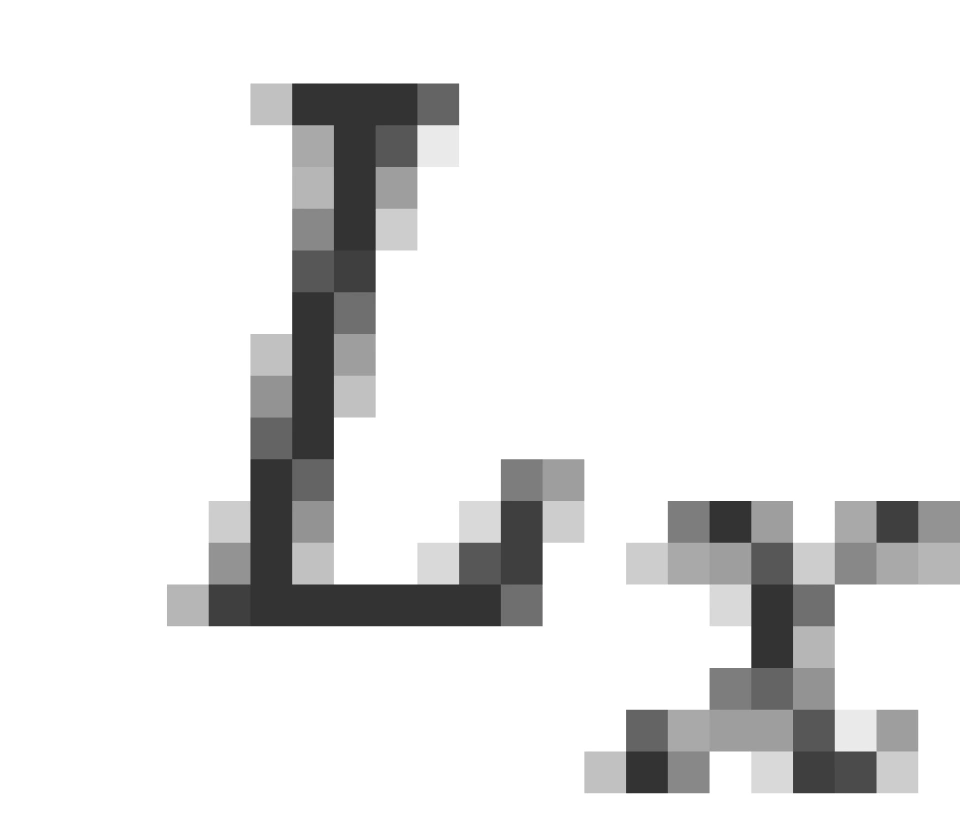
是确定的，但是
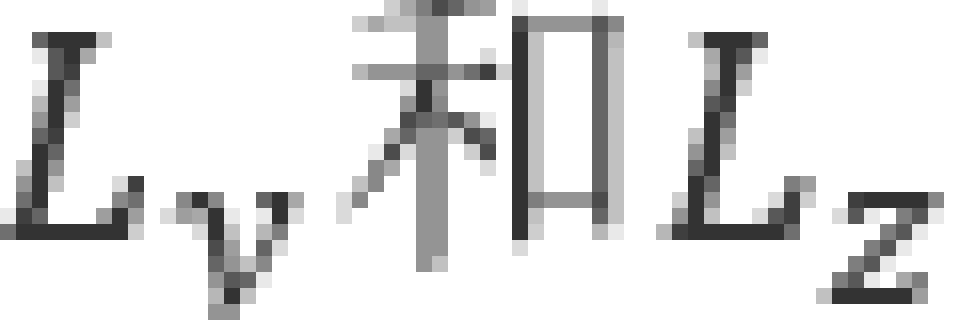就完全无法确定了。这是海森伯不确定性原理给出的结果。与
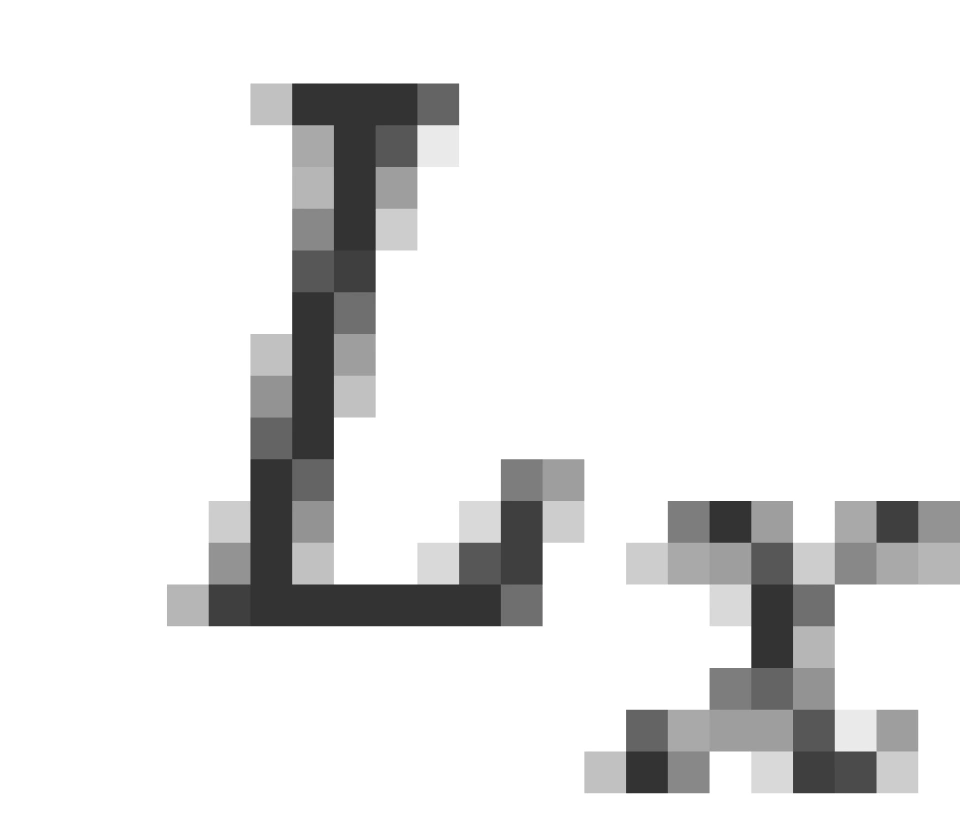对应的空间变量是方位角
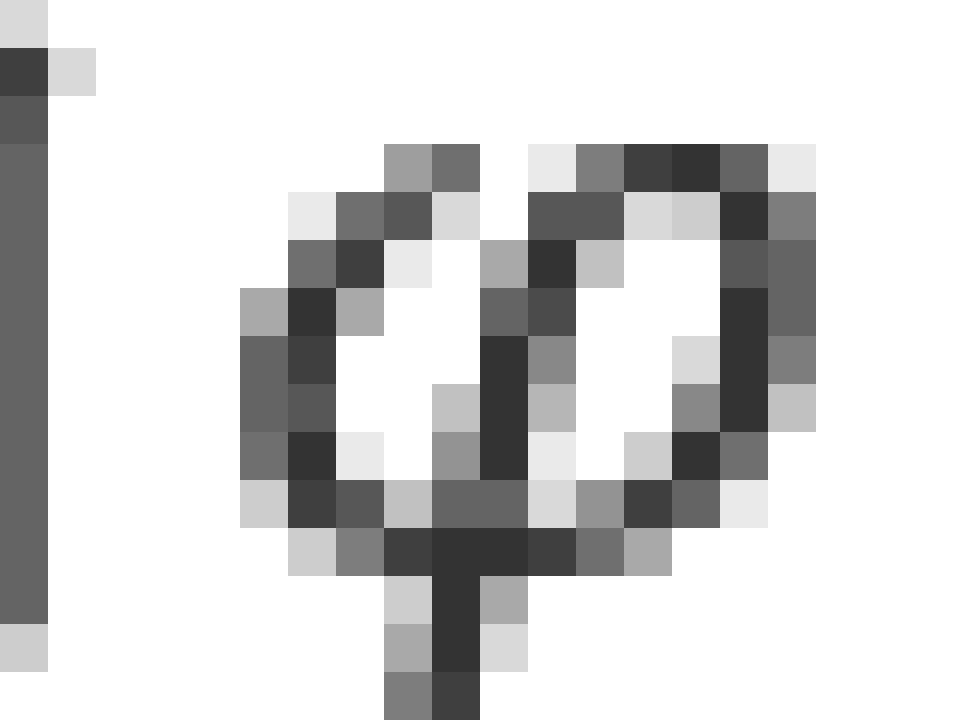，因此根据海森伯不确定性原理给出，沿x方向，有
而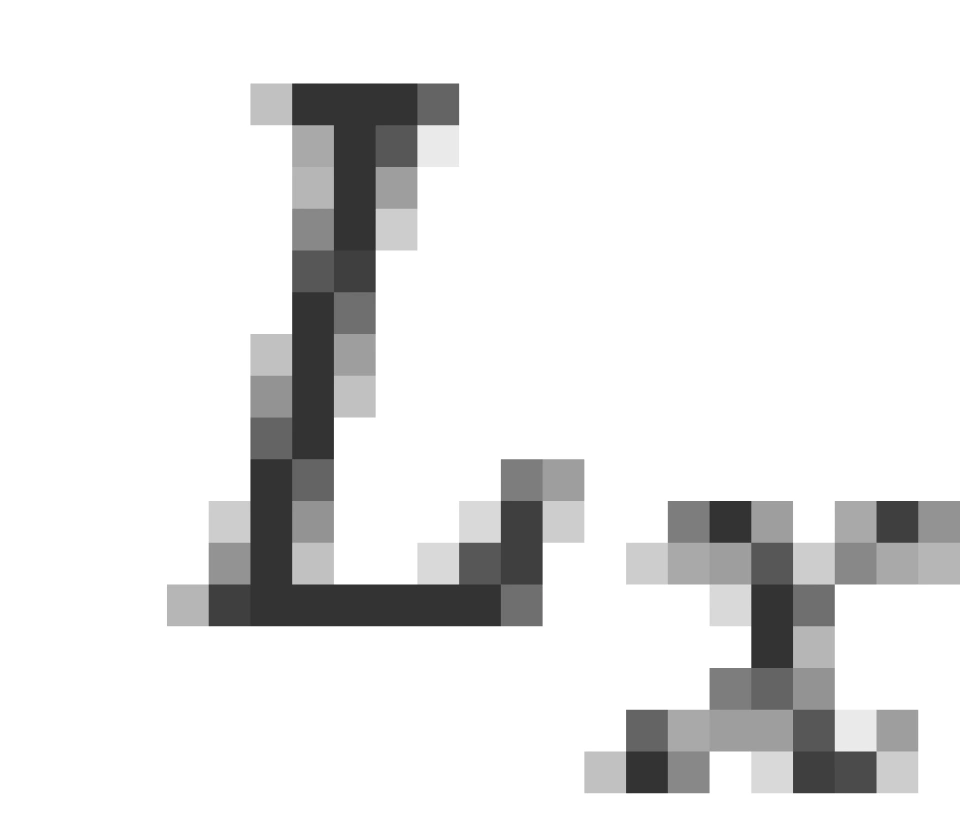的确定，意味着
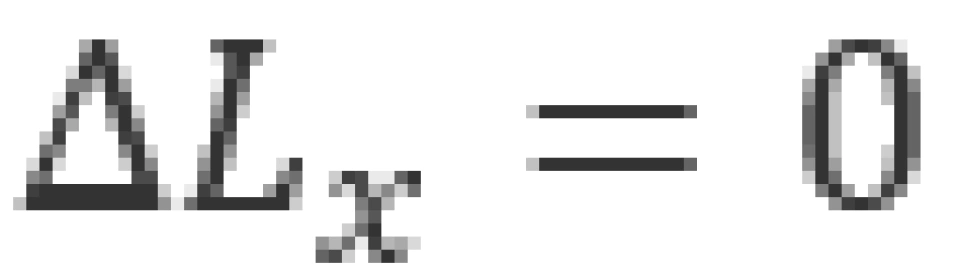，那么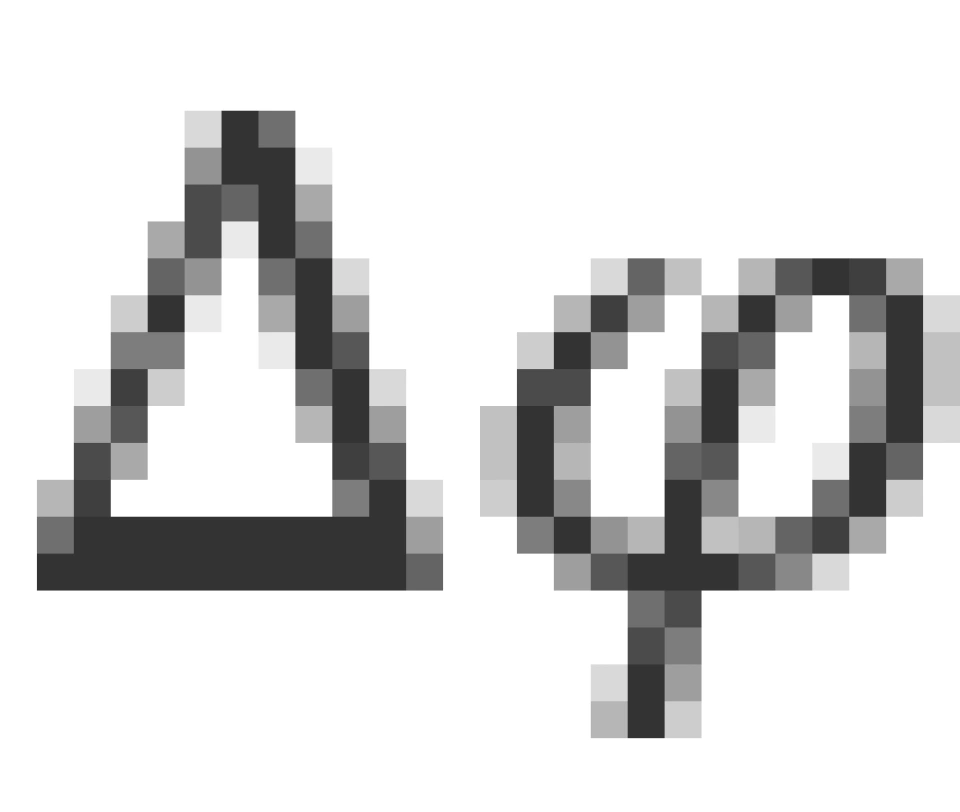
只能取无穷大，即
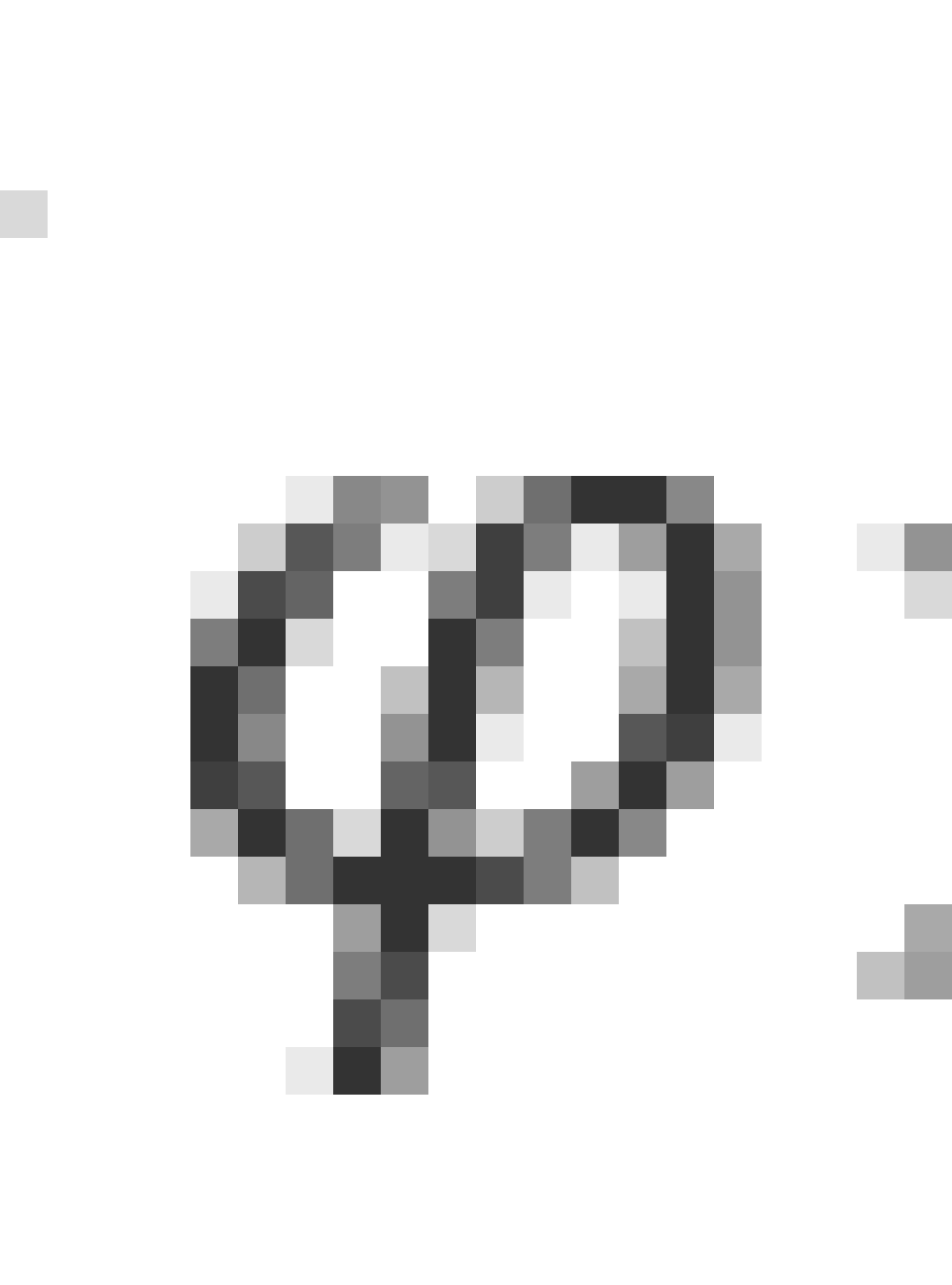是完全不确定的。这一结果可以用一模型理解，即电子到原子核的径矢绕x轴高速进动，那么这时
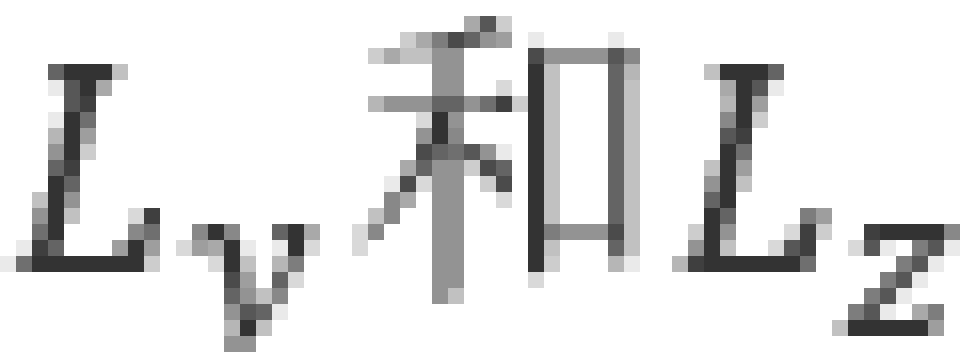的时间平均值为零，也就不可能对其进行测量了。
电子云
当一个电子波函数的上述三个量子数都确定之后，我们可以把这个波函数记作
对于一个基态氢原子，其电子满足以下条件
此时它的波函数为
那么此状态下，电子的概率密度就为
这是一个球对称分布。
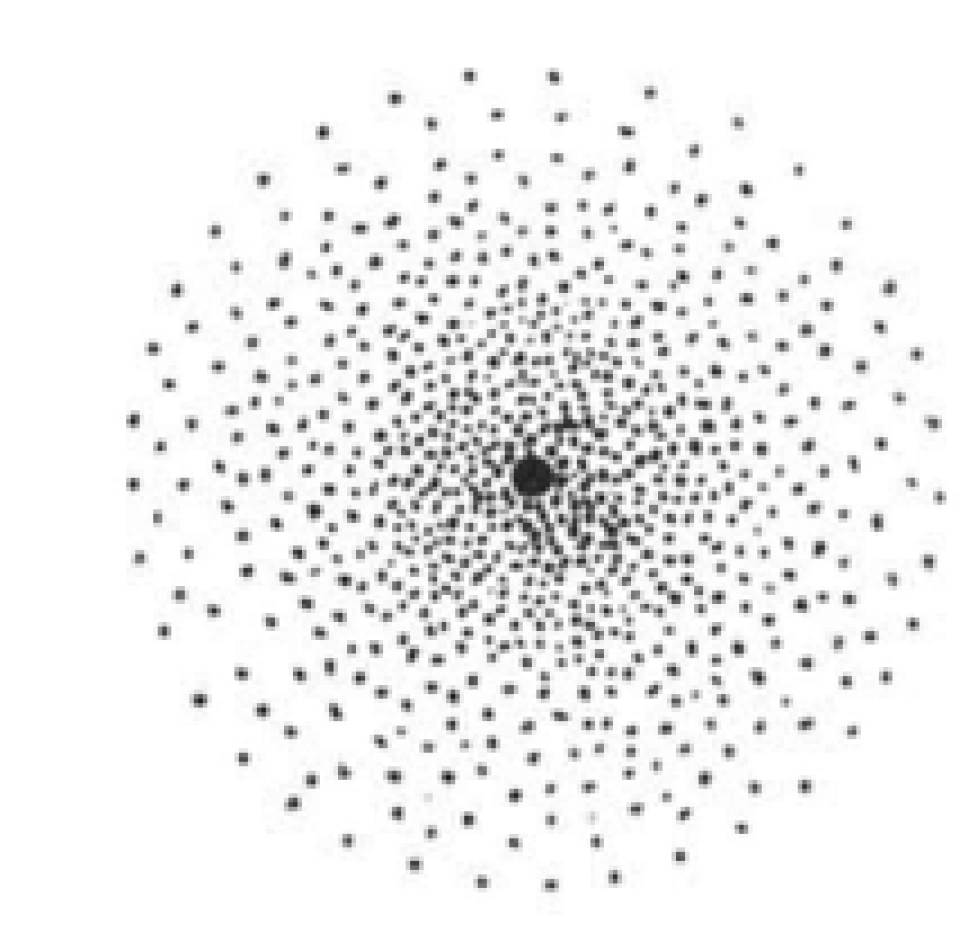
在化学分析中，我们通常会用点的密度来表示电子的概率分布，那么以上电子的概率分布就可以形象地由下图来表示。
由于电子对应的德布罗意波是概率波，只能对其位置进行概率密度的描述，因此电子具体的位置是模糊不清的，所以通常把以上的图叫做“电子云”。
有必要指出，上面提到的轨道角动量中所加的“轨道”二字是玻尔原子模型的产物，不能理解为是电子沿某一封闭轨道运动的角动量，而应当理解为“和位置变化相关的”角动量。
次壳层
当n=2时，l可以取1和0两个值，即存在以下两种状态
①状态下，电子云的分布具有球对称性。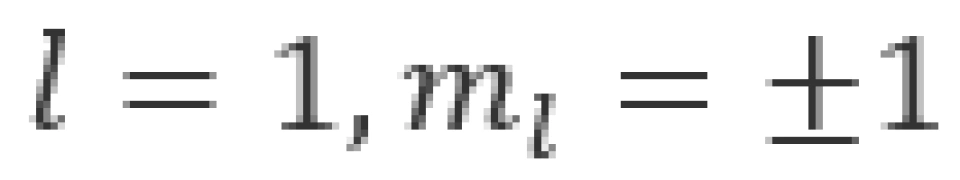
时，电子云的分布是完全一样的，它们与
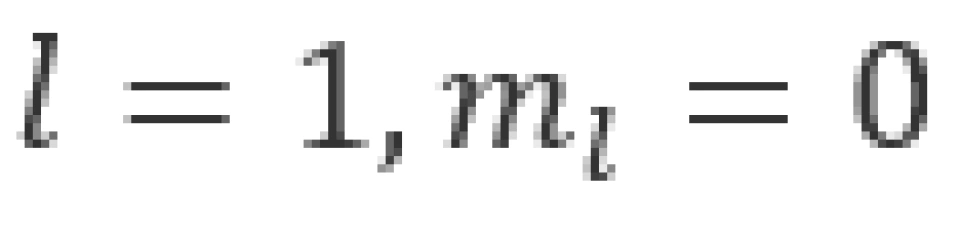的分布都具有关于轴的对称性。
对于一个孤立的氢原子来说，空间没有确定的方向，因此可以认为电子平均地在这三种状态之间往返。如果把三种状态下求出的概率密度加在一起，我们会发现，总和的概率密度也是球对称的。因此，我们把l=1的三个独立波函数归为一组。
通常来说，相同的波函数都可以归为一组，这样的一组叫做一个次壳层，其中电子概率密度的分布具有球对称性。我们习惯上把l=0，1，2…的次壳层命名为s，p，d…次壳层。
壳层
由上面提到的能量公式可以看出，氢原子的能量只与主量子数n有关，那么只要n相同，不同状态的能量都是相同的。这种现象叫做能级的简并，具有同一能级的各个状态叫做简并态。
具有同一主量子数n的各个状态都可以归为一组，这样的一组叫做一个壳层。我们习惯上地把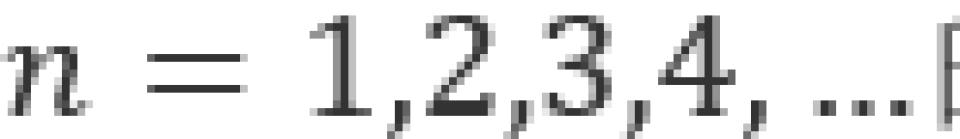
的各个状态依次命名为
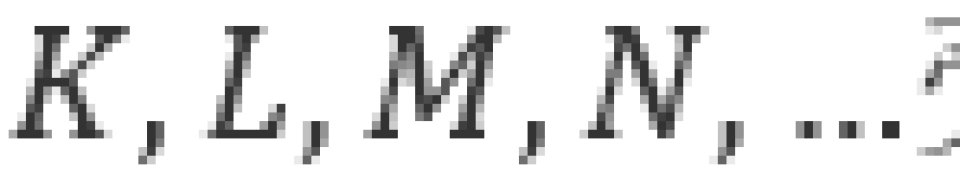壳层，主量子数为n的壳层内共有n个次壳层。
概率密度
概率密度是用于描述一个粒子出现在空间某处的概率大小的量。由于原子核内，库仑场势能具有球对称性，因此需要描述电子在原子内的概率分布，只需要求出概率密度关于径向距离的函数就可以了。因此我们通常需要求解径向概率密度。给径向概率密度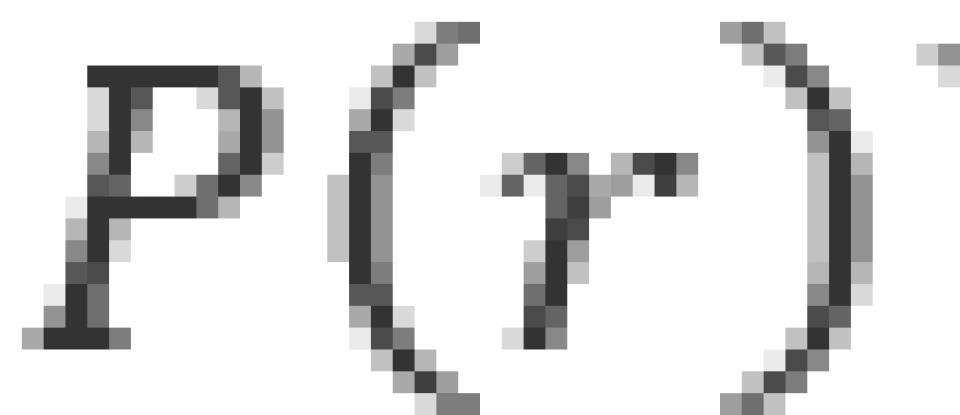
下定义——在半径为
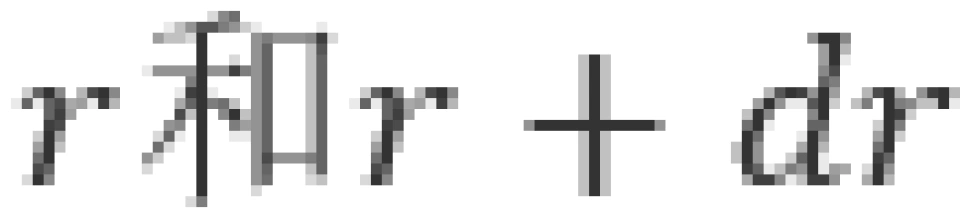的两个球面之间体积内，电子出现的概率密度为
。
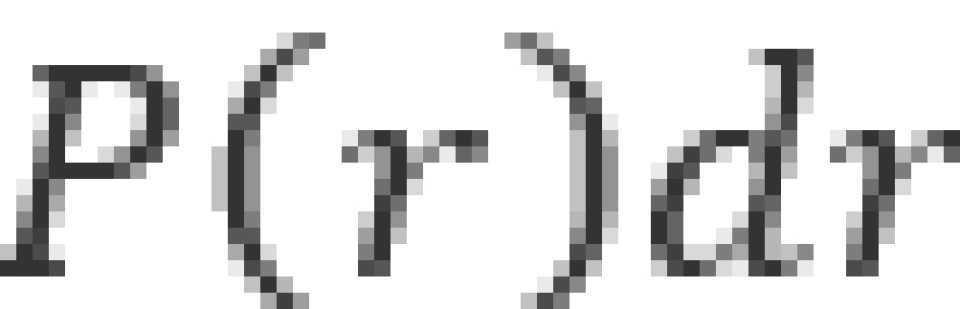对于基态的氢原子，取微分则有
即
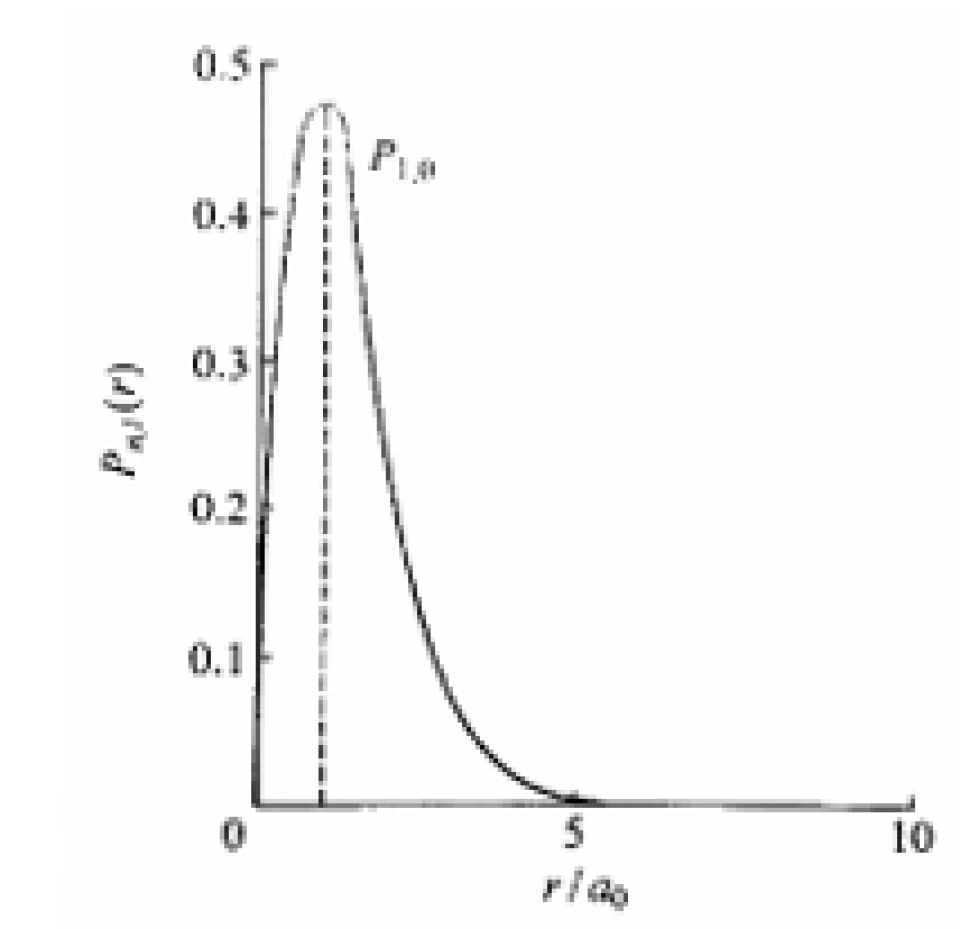
此式表示的径向概率分布曲线如下。
图中求得的极大值出现在r=a0处，即可以理解为，电子出现在距离核a0的位置上的概率最大，这正好符合了玻尔对氢原子电子轨道量子化的观测结果。
类似地，可以由同样的方法对不同能级、状态的电子云进行求解，并解析相应的电子云分布，这里就不再赘述了。
剩下的我们下期继续介绍。
参考引源：
《大学物理学》(张三慧等),《新概念物理教程》（赵凯华等）,Feynman Lectures on Physics, Learning Notes on Quantum Mechanics(Leng Xuan),Introduction to Quantum Mechanics(David J. Griffiths),Wikipedia,bilibili等。
图片来源：
百度图片,Google Images, 《大学物理学》(张三慧等)。
【本文为耀星会的原创作品，未经允许，禁止盗用、转载、篡改文章，否则耀星会和作者将追究版权责任。】
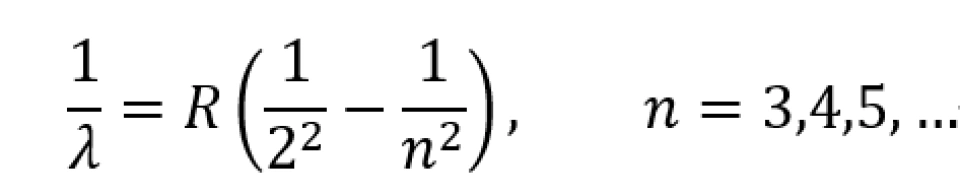
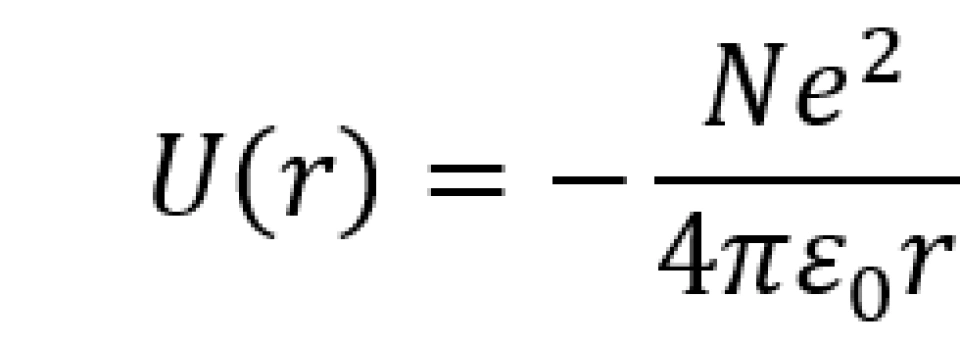
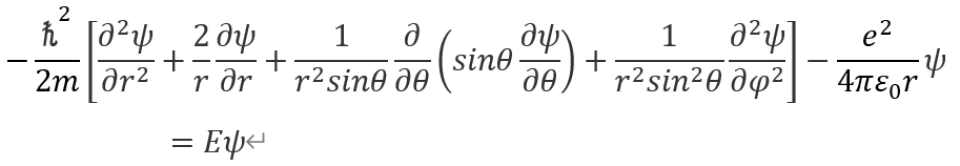
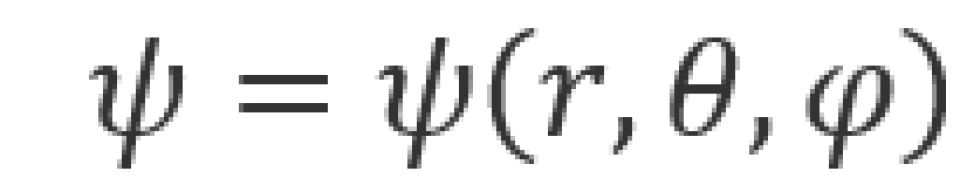
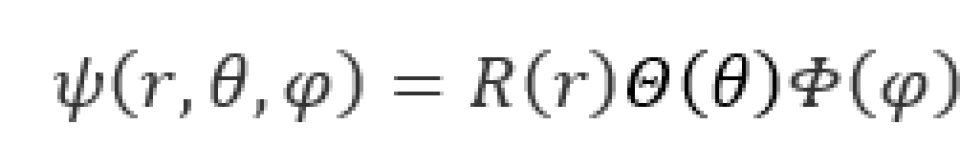
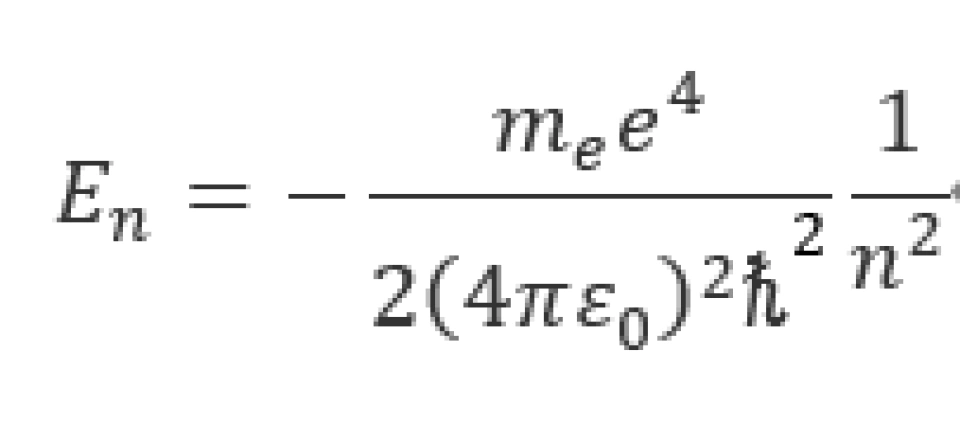
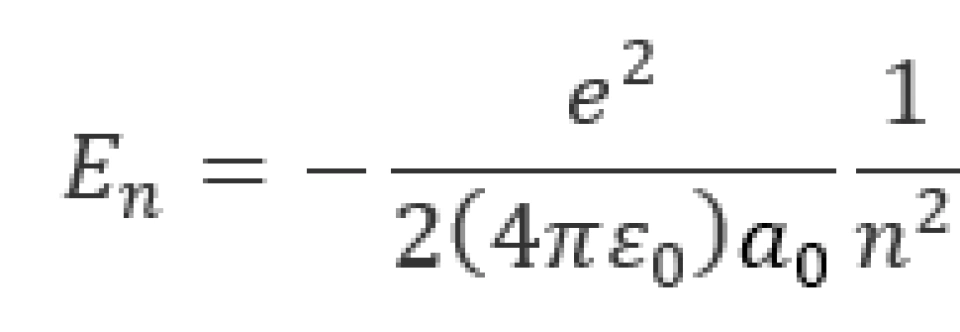
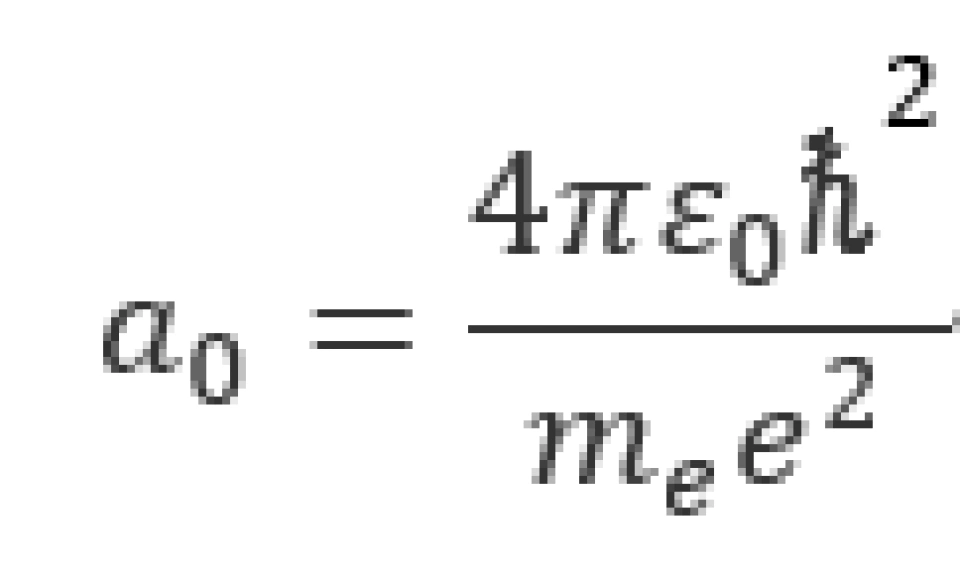
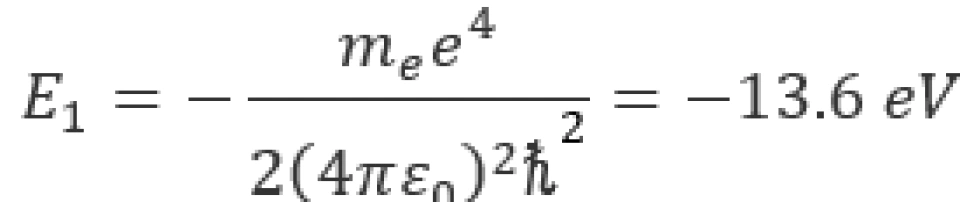
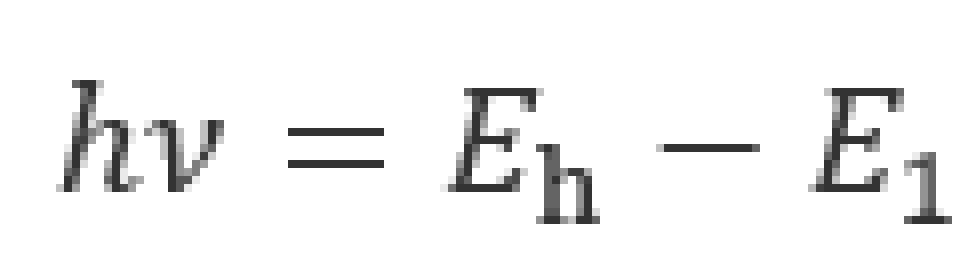
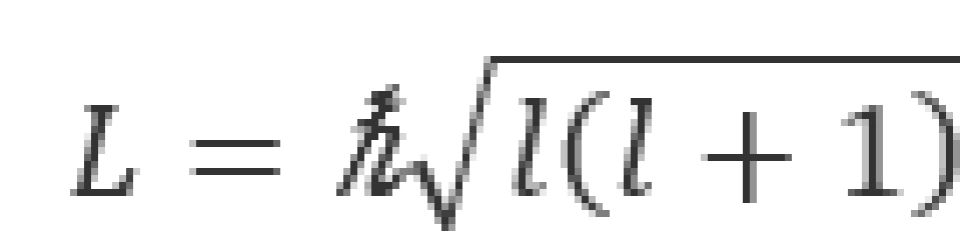
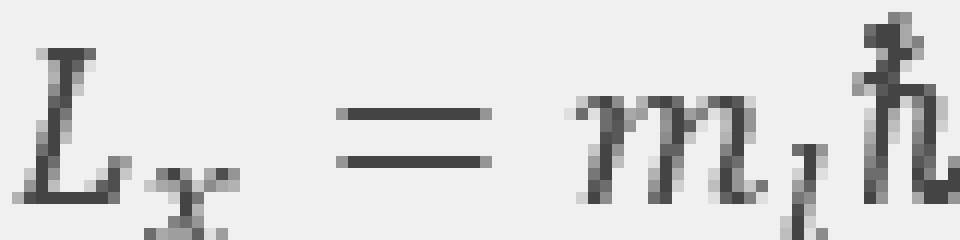
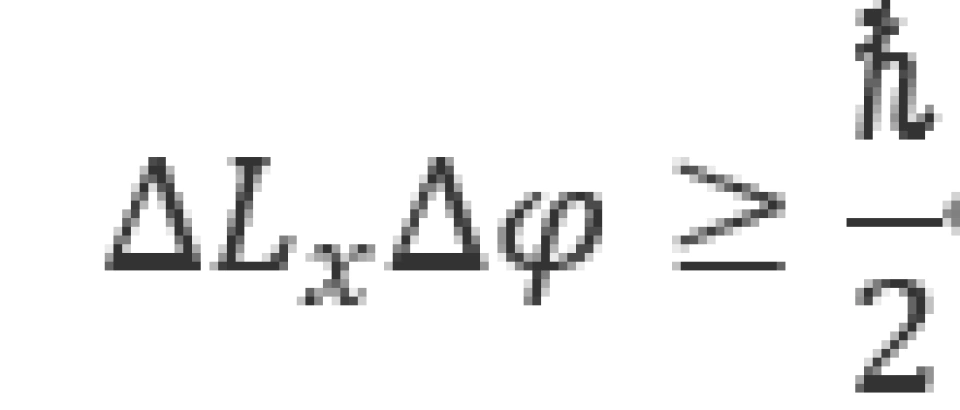
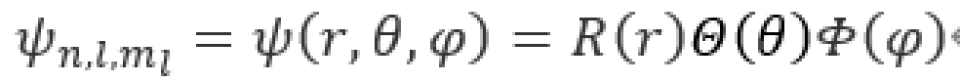
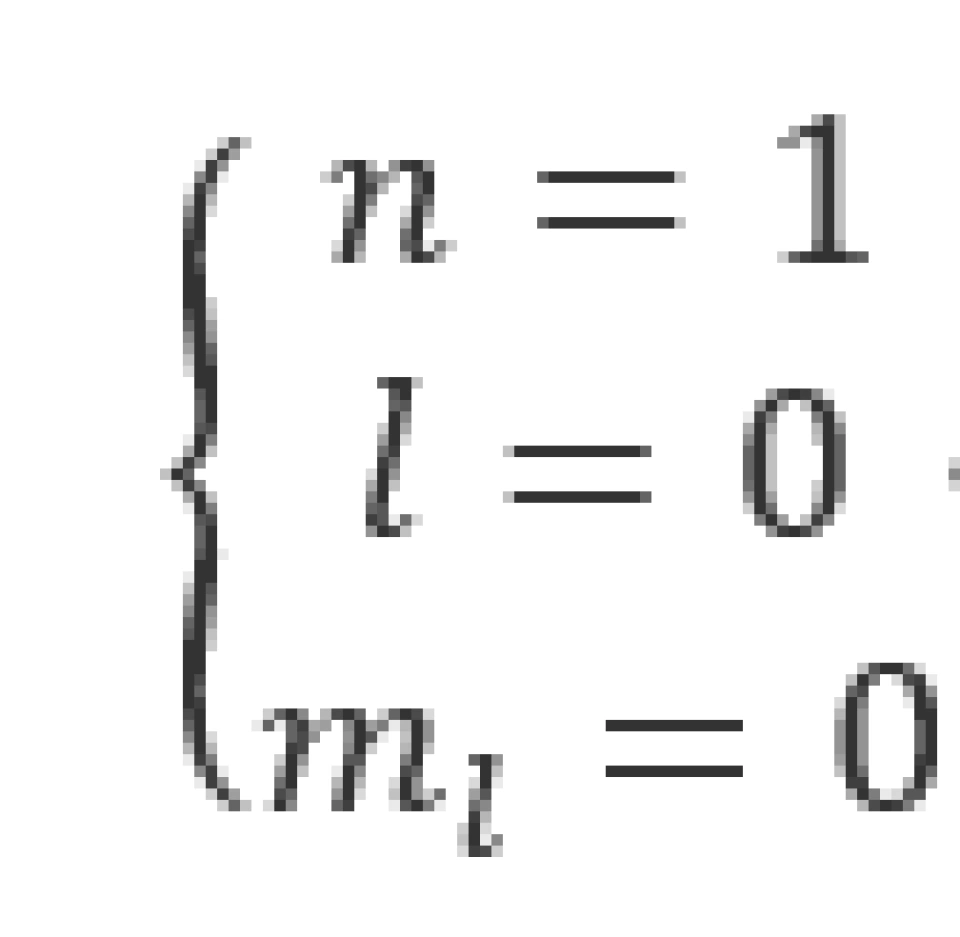
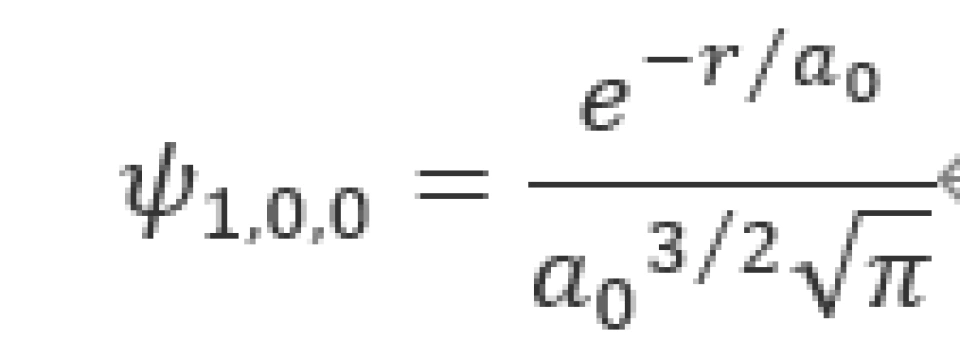
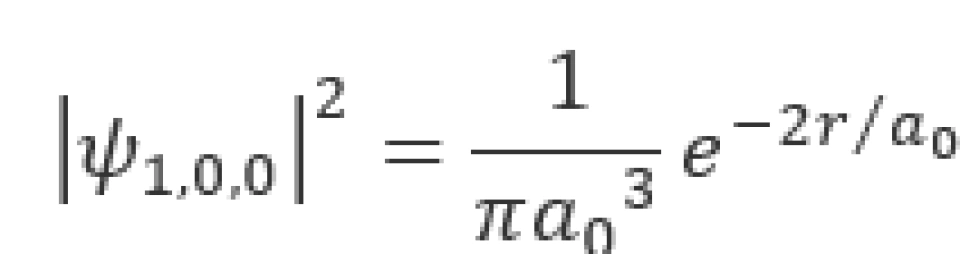
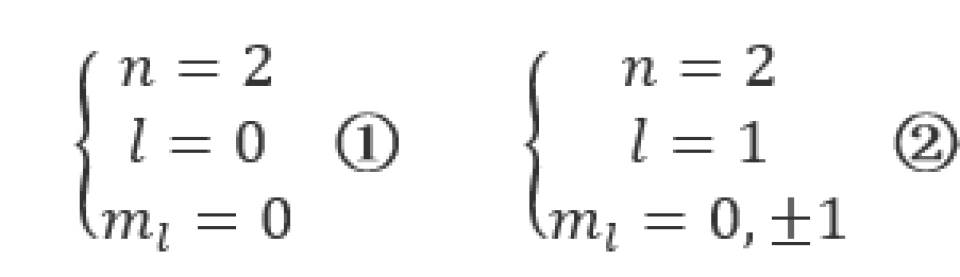
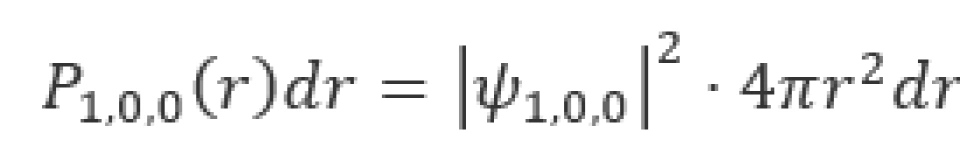
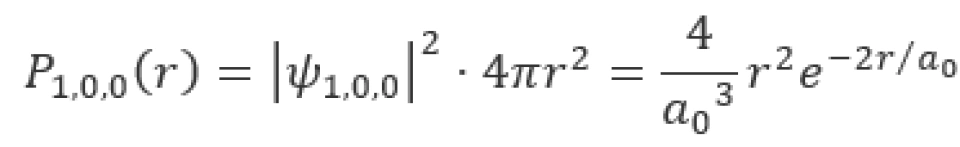
![[s-8]](https://www.bokeyuan.net/pic/image/emoji/cas/8.png)
