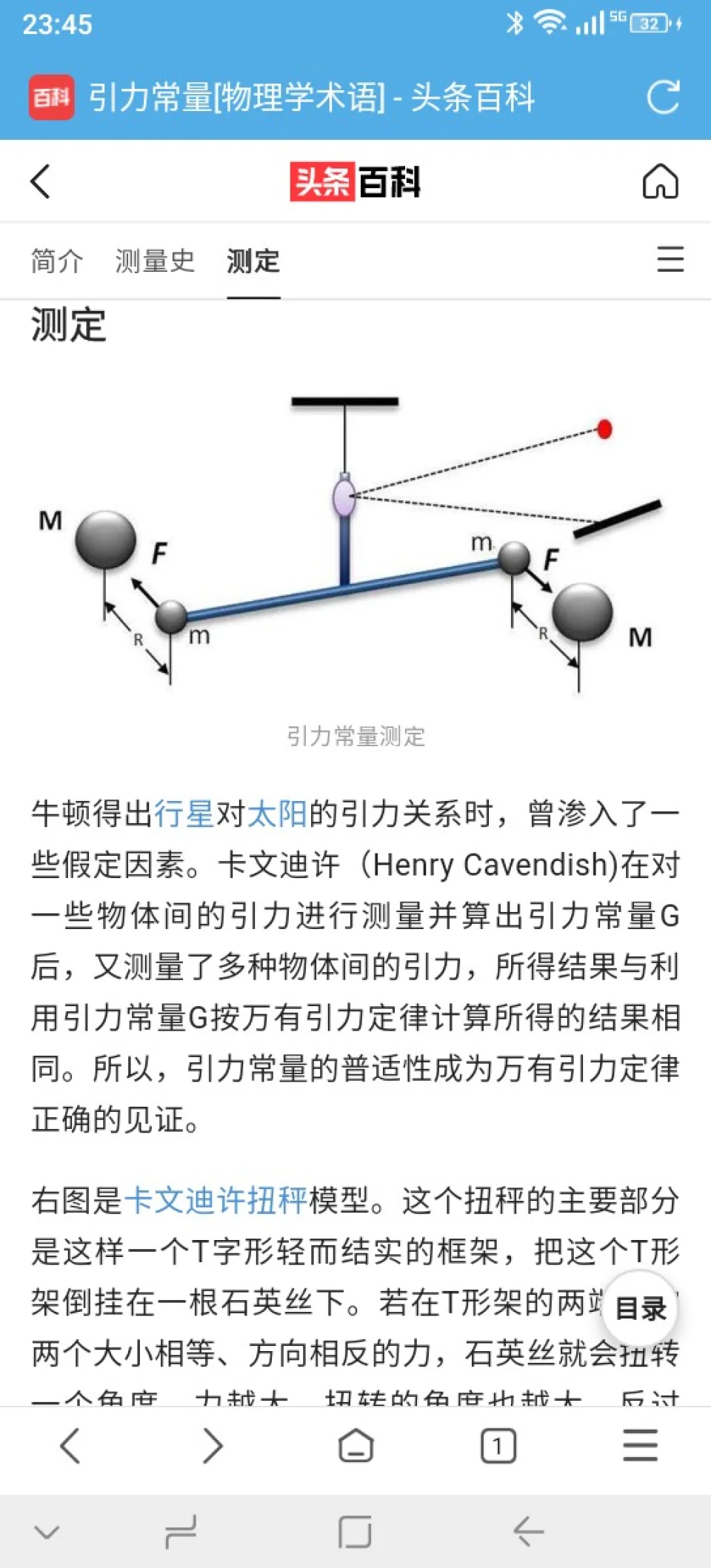
在物理学里，普朗克能量是普朗克单位制的能量单位，标记为Ep。用方程表达，普朗克能量是Ep=√hc5/G=1.956×109≈1.22×109GeV≈0.5433MWh
其中，c是光速，h是约化普朗克常数，G是万有引力常数。
在1991年观察到的超能量宇宙射线的能量大约为50焦耳。大多数的普朗克单位都是很小的数量。可是Ep的确是一个相当大的数量，大约是一个闪电所需要的能量。虽然，在粒子物理学里，Ep仍旧是一个很有用的物理量，特别是当我们需要包括重力效应的计算在内的时候。普朗克能量是侦测普朗克长度的尺寸所需的能量，可以说是在那区域内能容纳的最大的能量假若一个直径为1普朗克长度的圆球，包含有1普朗克能量，则这圆球会变成一个小黑洞。采用普朗克单位制，物理常数h,G与C 的数值都会等于1。因此，质能方程简化为E=m；其中，E是能量，m是质量。这样，普朗克能量与普朗克质量的数值相等。在广义相对论的方程里，G时常会有因子8π伴随。所以，在粒子物理学与物理宇宙学里，项目8πG时常被归一化为1。
普朗克单位制
普朗克单位制是一种计量单位制度，由德国物理学家马克斯·普朗克最先提出，因此命名为普朗克单位制。这种单位制是自然单位制的一个实例，经过特别设计，使得某些基础物理常数的值能够简化为1，这些基础物理常数是万有引力常数G，约化普朗克常数h，在真空里的光的光速c，库仑常数Ke=1/4π∈0，其中∈0是真空电容率，也就是电常数，玻尔兹曼常数KB。
上述每一个常数都至少出现于一个基本物理理论：G在广义相对论与牛顿的万有引力定律、h在量子力学、c在狭义相对论、∈0在静电学、KB在统计力学与热力学。实际上，以上的五个常数在许多物理定律的代数表达式中多次出现，因此引入普朗克单位制可以将这些代数表达式简化，普朗克单位制也因此成为了理论物理学一个非常有用的工具。在统一理论方面的研究，特别如量子引力学中，普朗克单位制能够给研究者一点大概的提示。
啊哈