科普驿站 第55期
科目:物理
难度:B2
讲师:咕咕叶
在经典力学中,质点的运动都沿着一定的轨道,在轨道上的任意一点都有确定的位置合动量。在牛顿力学体系中,我们也正是用位置和动量来描述一个质点在任一时刻的运动状态的。
在量子力学中,由于粒子的粒子性,我们可以谈论它的位置和动量。但由于其波动性,它的空间位置需要使用概率波来描述,而概率波只能给出粒子在各处出现的概率。因此,粒子在任一时刻都不具有确定的位置。与此相联系,粒子在各时刻也不具有确定的动量。粒子的动量和其位置遵循以下规律:
∆x∆p≥h/4π
其中∆x是粒子位置的不确定量,∆p是粒子动量的不确定量,h为普朗克常量。
依照电子单缝衍射实验来粗略推导不确定关系。
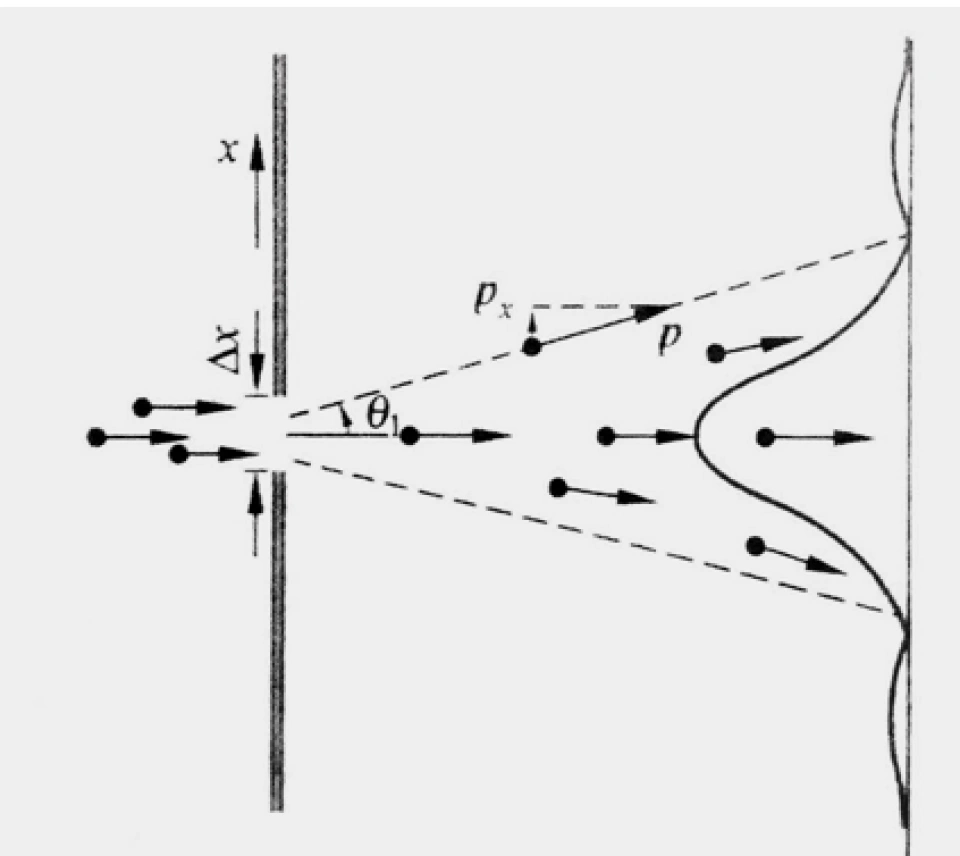
如图所示,我们考虑一个电子在通过缝隙时发生衍射的状况。由于德布罗意波的概率特征,我们不能说电子是从缝中的哪一点通过的,而只能说它是从宽为∆x的缝中通过的。因此,电子在x方向上位置的不确定量就是∆x。
给定电子具有一个动量p,将矢量p进行分解,可以得到,p在x方向上的分量为p_x。由于过缝前,p_x=0,而过缝后p_x便发生了变化。因此,p_x受以下不等式约束:
0≤p_x≤psinθ_1
则动量p在x方向上的不确定量为
∆p_x=psinθ_1
考虑到衍射条纹的次级极大,即电子在如图虚线外部分的概率幅不为0,应改写为
∆p_x≥psinθ_1
θ_1=arcsin λ/∆x
又根据德布罗意波长
λ=h/p
可得
sinθ_1=h/p∆x
将此式代入整理可得
∆x∆p_x≥h
更一般的理论给出
∆x∆p_x≥h/4π
引入另一个常用的量,即约化普朗克常量
ℏ=h/2π=1.0545887×10^(-34) J∙s
上式通常改写为
∆x∆p_x≥ℏ/2
这就是位置坐标与动量的不确定关系。观察式子,左侧为动量与位置的不确定量,式子右侧为一常数,这说明动量与位置的不确定量呈反比。在测量一个粒子的位置或动量时,其中一个量测得越精准,另一个量就越模糊。又因为两个不确定量都不能为0,所以对粒子动量和位置测量的精度存在一个不可逾越的极限。
不确定性原理是海森伯于1927年给出的,它的根源是波粒二象性。费曼曾把它称为“自然界的根本属性”。事实上,所有物质的量子力学理论都有赖于不确定性原理的正确性。
除了位置和动量的不确定关系以外,对粒子的行为说明常常还用到能量和时间的不确定关系,下面简略看一下推导过程。
采用非相对论形式下的能量-动量关系。考虑一个粒子用一个波包来描述,波包宽度为∆x,群速度为v,相当于经典粒子的运动速度。波包掠过空间某点所需的时间为Δt=Δx/v。因其动量不确定度为
∆p≥ℏ/2∆x
其能量不确定度为
∆E≈∂E/∂p ∆p=∂(p^2/2m)/∂p ∆p=v∆p
所以
∆E∆t≈∆x/v v∆p=∆x∆p≥ℏ/2
∆E∆t≥ℏ/2
这就是关于能量与时间的不确定关系。在做数量级估算时,往往用ℏ代替ℏ/2。
薛定谔方程
在经典力学中,在给定的已知条件下,质点的运动是唯一确定的,它们都统一遵守牛顿三大定律。
在经典力学中,一个质点的基本动力学方程是牛顿第二定律的方程
据此,我们可以对任一粒子的行为进行计算模拟。但是在量子力学中,粒子具有波粒二象性,因此我们不能再单一地用方程对粒子的粒子性进行矢量描述了——我们还需要考虑粒子相对应德布罗意波的波函数。
1925年,德拜让他的学生薛定谔作一个有关德布罗意波的学术报告。报告后,德拜提醒薛定谔:“对于波,应当有一个波动方程。”薛定谔此前就曾注意到爱因斯坦对德布罗意假设的评论,此时又受到了德拜的鼓励,于是就努力钻研。几个月后,他就向世人拿出了一个波动方程,这就是薛定谔方程——量子力学的基本动力学方程。
作为一个基本方程,它不能由其他更基本的方程推导出来,而只能通过某种方式建立起来。在介绍薛定谔当初是如何“猜”和“凑”出方程的之前,我们先看看薛定谔方程的一维形式
-ℏ^2/2m (∂^2 Ψ)/(∂x^2 )+U(x,t)Ψ=iℏ ∂Ψ/∂t
式中,Ψ=Ψ(x,t)是质量为m的粒子在势场U=U(x,t)中运动的波函数。由于式中时间t也是一个变量,我们先不全面讨论这样的含时薛定谔方程,下面只讨论在恒定势场U=U(x)中运动的情形。接下来简单看一下数学过程。
作为波函数,它应当是包含时间的周期函数,因此波函数应有以下形式
Ψ(x,t)=ψ(x) e^((-iEt)⁄ℏ)
观察形式,式子右侧为波函数空间部分与时间部分的乘积。
将此式代入薛定谔方程,可知波函数的空间部分应当满足的方程为
-ℏ^2/2m (∂^2 ψ)/(∂x^2 )+Uψ=Eψ
此方程不含时间因子,称为定态薛定谔方程,其中ψ=ψ(x)叫做粒子的定态波函数,它描述的粒子状态叫定态。
关于薛定谔方程,有两点条件需要说明。
1、它是线性微分方程。这就意味着作为它们的解的波函数或概率幅都满足叠加原理。
2、从数学上来说,对于任何能量E的值,方程都有解,但并非所有解都具有物理意义。作为有物理意义的波函数,这些解必须是单值的,连续的,有限的。
令人惊奇的是,根据这些条件,薛定谔方程可以“顺理成章地”得到微观粒子量子化的条件。这些量子化条件在普朗克和玻尔那里都是“强加”给微观系统的假设。
对于粒子的三维运动,通常使用薛定谔方程的球坐标形式
-ℏ^2/2m [(∂^2 ψ)/(∂r^2 )+2/r ∂ψ/∂r+1/(r^2 sinθ) ∂/∂θ (sinθ ∂ψ/∂θ)+1/(r^2 〖sin〗^2 θ) (∂^2 ψ)/(∂φ^2 )]+Uψ=Eψ
其中r为粒子的径矢的大小,θ为极角,φ为方位角。
下面介绍薛定谔建立方程的大致过程:
薛定谔注意到,德布罗意波的相速度与群速度(非相对论情形)的区别。德布罗意波的相速度为
u=λν=E/p=E/√(2mE_k )=E/√(2m(E-U) )
其中m为粒子的质量,E为粒子的总能量,U=U(x,y,z)为粒子在给定的保守场中的势能。对于一个波,薛定谔假设其含时的波函数通过一个振动因子
exp[-iωt]=exp[-2πiνt]=exp[-2πi E/h t]=exp[-i E/ℏ t]
和时间t有关,于是有
Ψ(x,y,z,t)=ψ(x,y,z)exp[-i E/ℏ t]
下面就一维情形进行讨论。
由此式可得粒子的概率密度为
|Ψ|^2=ΨΨ^*=ψ(x) e^((-iEt)⁄ℏ) ψ(x) e^(iEt⁄ℏ)=|ψ(x)|^2
此概率密度与时间无关,因此上面得出的ψ=ψ(x)为粒子的定态波函数。
将以上式子代入波动方程的一般形式
(∂^2 Ψ)/(∂x^2 )=1/u^2 (∂^2 Ψ)/(∂t^2 )
稍加整理可得
-ℏ^2/2m (∂^2 ψ)/(∂x^2 )+Uψ=Eψ
由于ψ=ψ(x)为粒子的定态波函数,则以上微分方程就是粒子的定态薛定谔方程。
原子系统可以从一个定态转变到另一个定态。例如在氢原子的发光过程中,原子的能量E将发生变化。薛定谔注意到这种随时间的变化,因此认为这时E不应该出现在方程中,于是可将粒子的定态波函数换写为
ψ(x)=Ψe^(iEt⁄ℏ)
将此式代入定态薛定谔方程,得到
-ℏ^2/2m (∂^2 Ψ)/(∂x^2 )+UΨ=EΨ
又因为
EΨ=iℏ ∂Ψ/∂t
则可得到
-ℏ^2/2m (∂^2 Ψ)/(∂x^2 )+UΨ=iℏ ∂Ψ/∂t
式中的U也可推广至时间t的函数U(x,t),这便是含时薛定谔方程。
参考引源:
《大学物理学》(张三慧等),《新概念物理教程》(赵凯华等),Feynman Lectures on Physics, Learning Notes on Quantum Mechanics(Leng Xuan),Introduction to Quantum Mechanics(David J. Griffiths),Wikipedia,bilibili等。
图片来源:
百度图片,Google Images, 《大学物理学》(张三慧等)。
【本文为耀星会的原创作品,未经允许,禁止盗用、转载、篡改文章,否则耀星会和作者将追究版权责任。】


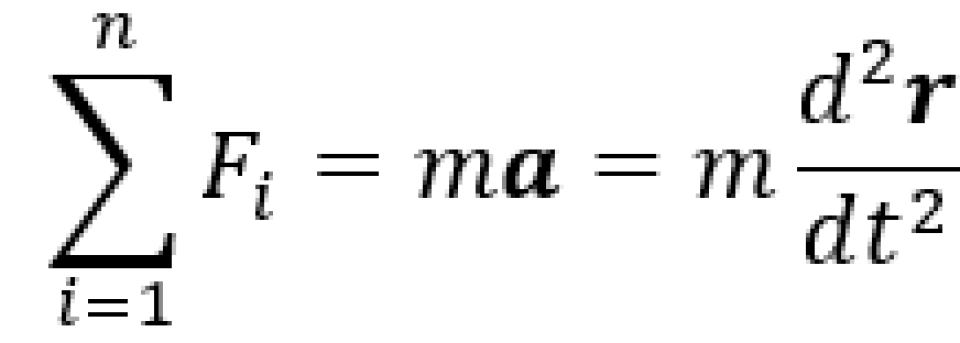

![[s-1]](https://www.bokeyuan.net/pic/image/emoji/cas/1.png)
![[s-70]](https://www.bokeyuan.net/pic/image/emoji/cas/70.png)
![[s-2]](https://www.bokeyuan.net/pic/image/emoji/cas/2.png)
![[s-14]](https://www.bokeyuan.net/pic/image/emoji/cas/14.png)











