物理上,有理想模型“质点”,它在研究物理现象上忽略了形状、体积等因素,只考虑其质量和运动轨迹与状态。
而运动只有在选定参考系后才拥有意义,质点相对于参考系,在一段时间内位置连续变化,以初位置为起点并指向末位置的有向线段,称为质点在这段时间里,相对于参考系的位移。该位移记作德尔塔r(△r)。
它是一个有大小和方向的矢量,它的运算符合平行四边形法则,在曲线运动中,质点的位移与路程并不相同。在特殊情况下,质点运动回到初位置,它的位移为零,但是它的路程并不为零。因为位移只取决于在选定参考系下的初末位置,而路程取决于质点的运动轨迹。
而质点位于初位置,经过一段时间后运动到末位置,这一段时间记作德尔塔t(△t),此时质点的位移为△r,而位移矢量的在这段时间内的变化率称为速度,也为矢量,用v进行表示。当时间变化量较大时,位移与时间间隔的比值称为平均速度,当时间变化量极小时,该比值称为瞬时速度,也就是说,t时刻的瞬时速度为在该时刻位移与时间变化量的比值。此时它就等于位移矢量关于时间t的导数。
因为位移是一个矢量,那么速度也是矢量。速度的大小称为速率,即瞬时速度的大小为瞬时速率。因为瞬时速度能详细反应质点在该时刻的运动情况,所以如果没有特别说明,则一般的速度作为瞬时速度计算。
质点在做曲线运动时瞬时速度的方向,沿着该点所在切线方向。如果质点的运动轨迹是直线,则该质点做的是直线运动,否则为曲线运动。如果质点运动的瞬时速率不变,可分为匀速直线运动或匀速曲线运动(若运动轨迹为圆周,则称为匀速圆周运动)。
因为速度是时间的函数,那么速度关于时间的变化率称为质点的加速度,也为矢量。在一段时间内,△t内速度的变化量记作△v。而速度随时间的变化率称为质点在t时刻的瞬时加速度,简称加速度。如果没有特别说明,加速度一般指瞬时加速度。
质点在做曲线运动时,加速度方向一定不与运动切线方向相同,而△v与△t的比值,在△t无限趋近于零时,即速度关于时间的导数,为该时刻瞬时加速度,也等于位移关于时间的二阶导数。对于加速度保持不变的运动统称为匀变速运动,包含类型很多,如匀变速直线运动、抛体运动等,匀速圆周运动的速度与加速度时刻改变,因为方向时刻改变,但速度与加速度大小不变。 作者:胡杨
参考文献:《理论力学教程周衍柏》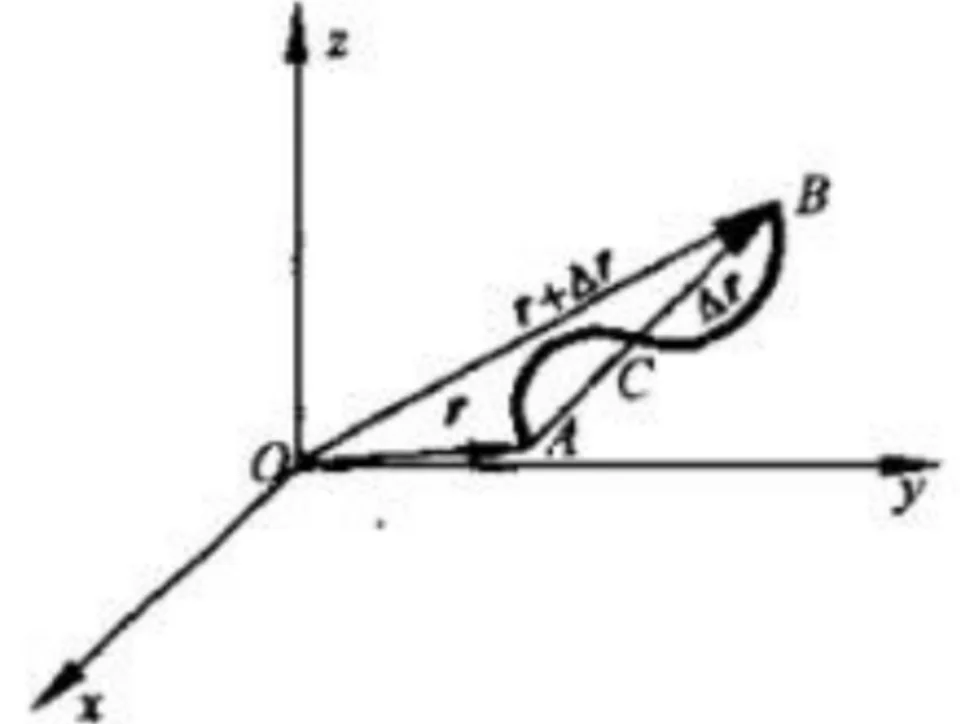
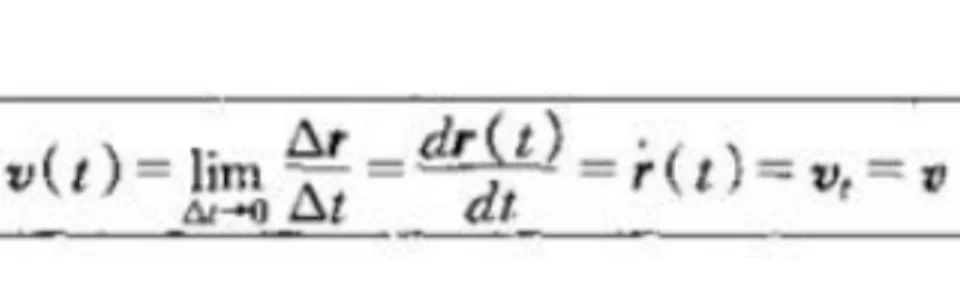
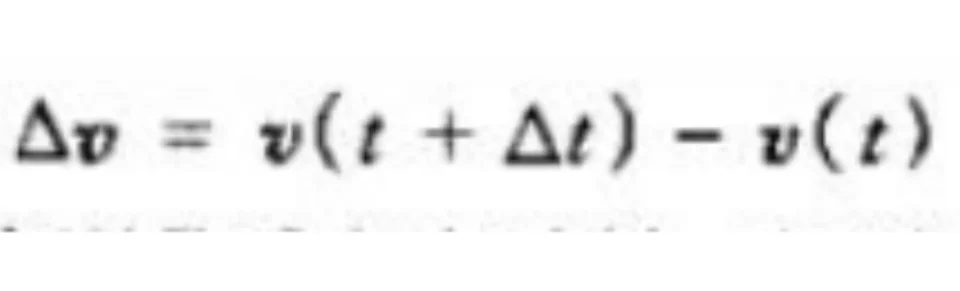
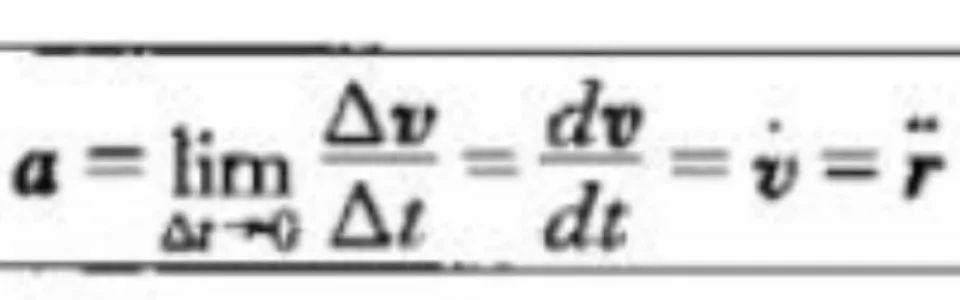



![[s-70]](https://www.bokeyuan.net/pic/image/emoji/cas/70.png)
![[s-1]](https://www.bokeyuan.net/pic/image/emoji/cas/1.png)
![[s-2]](https://www.bokeyuan.net/pic/image/emoji/cas/2.png)











