磁化电流和位移电流也是两种等效电流,顾名思义,也都是为解释磁性而引入的。换句话说,它们已经脱离了“电荷运动”这一电流的基本特征了!
先来看磁化电流
人们发现磁是电的运动导致的(暂不考虑自旋这种内禀性质对磁性的解释),为了解释天然磁性,法国物理学家安培提出了“分子环流”假说。
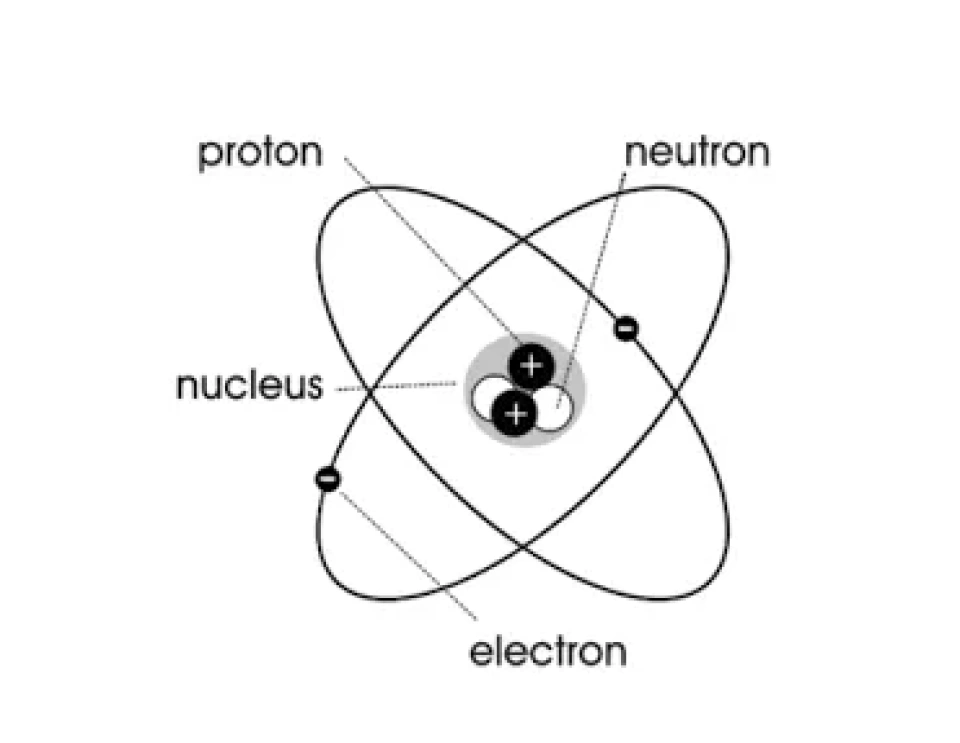
如下图所示,任何一个原子或分子,都可以看作有电荷绕着中心旋转,总体形成一个微小的环电流,即“分子环流”。
根据电流激发磁场的规律,这个分子环流将产生一个叫做磁矩的物理量。
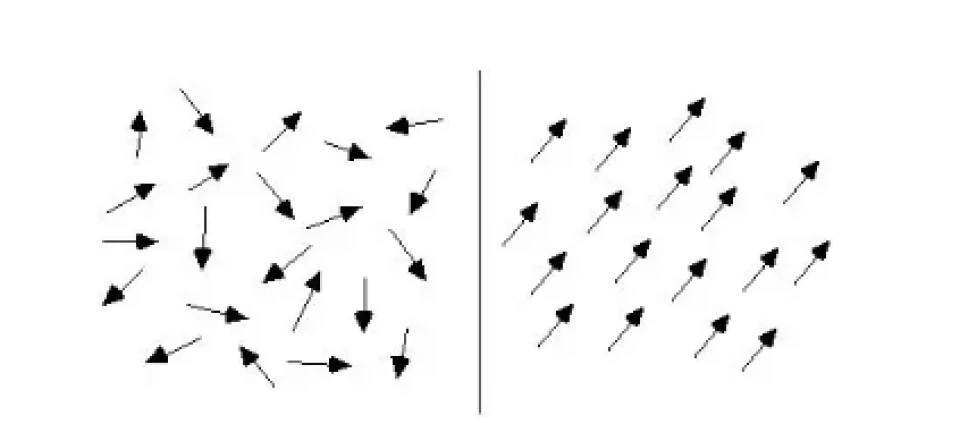
一般情况下,物质的分子环流排列是混乱的,因此物质不显磁性,如下图左边所示。当受到外磁场作用时,这些分子环流将大致整齐排列。如下图右边所示,它们的磁矩尽可能沿一个方向排列,就像无数个小磁针聚集在一起,形成一个总的磁场,由它们构成的物质整体就呈现磁性了。
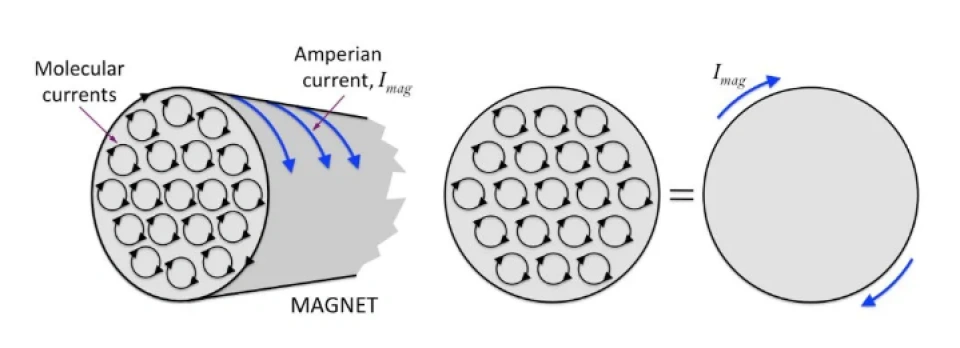
假设有一个圆柱形磁铁,内部的分子环流排列整齐,那些处在磁铁截面边缘处的每个分子环流的一段连在一起,形成一个大的环流,如下图所示。
据此我们可认为,一个条形磁铁就像一个通电螺线管一样。换句话说,磁铁的表面有看不见的电流缠绕着!这种电流无法被接出来使用,它被局限在磁体的表面,我们称之为“束缚电流”,或叫“磁化电流”。
所以,磁化电流之所以是电流,因为它与真实的电荷运动形成的电流一样,能等效地产生磁场!
再来看位移电流
根据安培环路定理,磁场强度对闭合路径的积分等于以此路径为边界的任意曲面上的电流密度的通量,即
这个定理在数学上叫斯托克斯定理。它告诉我们,矢量沿着任意闭合路径的积分,一定等于它的旋度对以该闭合路径为边界的任意曲面的通量。
麦克斯韦发现, 当面对非稳恒电流电路时,安培环路定理却出现了矛盾。
典型的非稳恒电流出现在电容器充电和放电过程中。
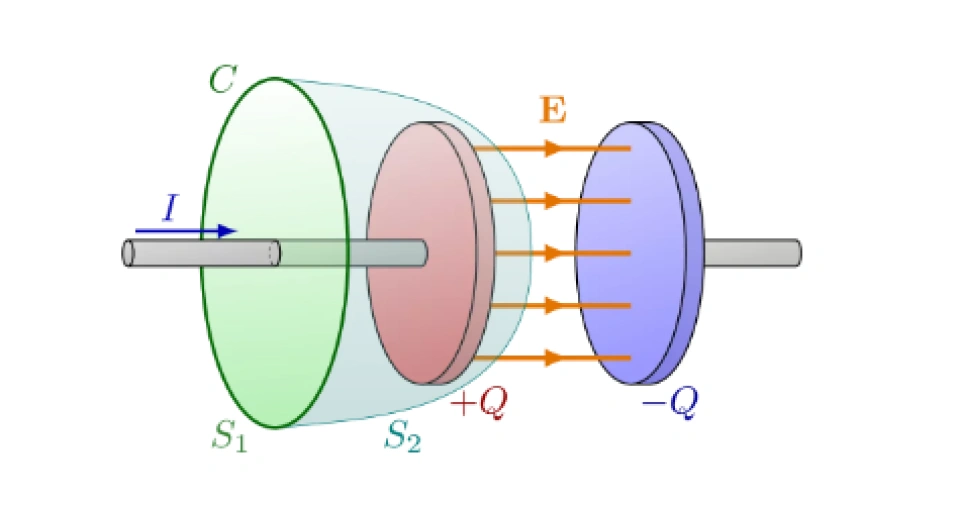
设我们考虑某绕过导线的闭合路径,如下图所示中的C所标识的圆形,以它为边界的曲面可以任意选择,图中选择了C本身围住的圆平面S1,以及跨过电容器左极板的曲面S2。
但作为磁场强度的环路积分,它的值应该是确定的。
安培环路定理必须成立,现在出了问题,那必然是因为有一部分电流之前没有被我们发现。
无论充电还是放电,每时每刻,电容器极板之间存在一个与电流大小和方向都同步的物理量。它就是电位移矢量的通量的时间导数。
那么完整的电流公式为
也就是说,极板间电路虽然断开了,但电位移通量的导数和电流之和一起,作为一个整体,时刻保证了电流的连续性。
现在知道了,按照斯托克斯定理的要求,当对闭合曲面计算电流密度的通量时,位移电流的密度也应该考虑。
故完整的安培环路定理是
这种电流不是一种数学上的弥补,而是切实存在的东西,只不过之前没发现而已。
为什么说它是本来就存在的呢?因为它作为电流,与传导电流一样,等效地激发磁场,只不过没有电荷的运动,不需要导线引导,也不能产生焦耳热,因此一直被忽略了。
换句话说,当我们面对磁场时,原先对于电流的定义太狭隘了。电流的本质不是电荷的运动,它应该是一种能激发磁场的东西。
电流的几种存在的形式都介绍完了。它们都是客观存在的,它们的共同之处是:所有的电流都能等效的激发磁场。


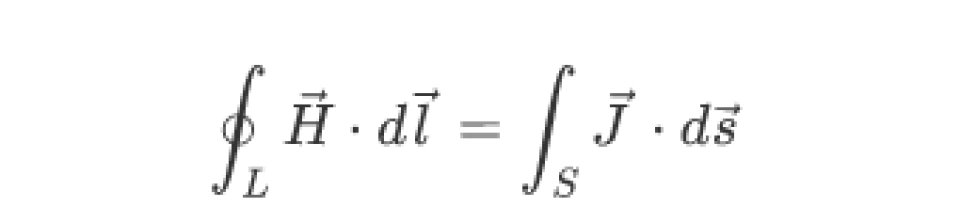
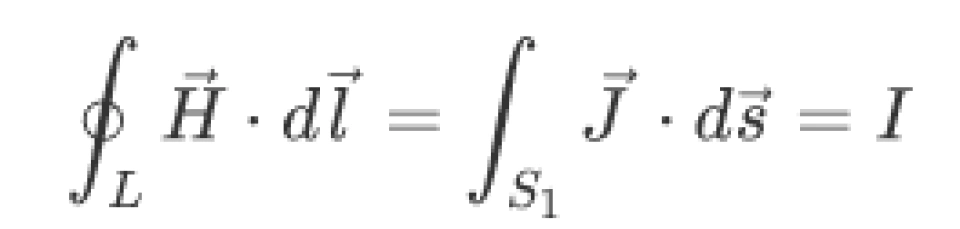
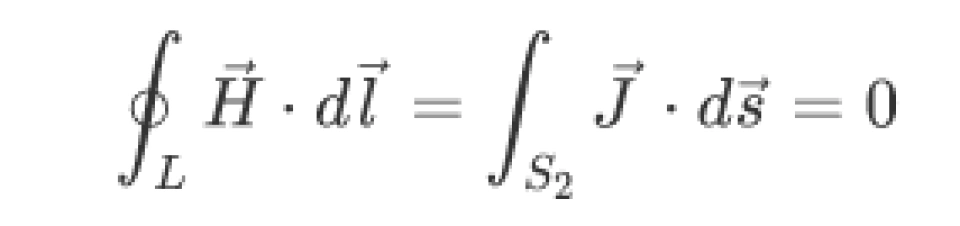
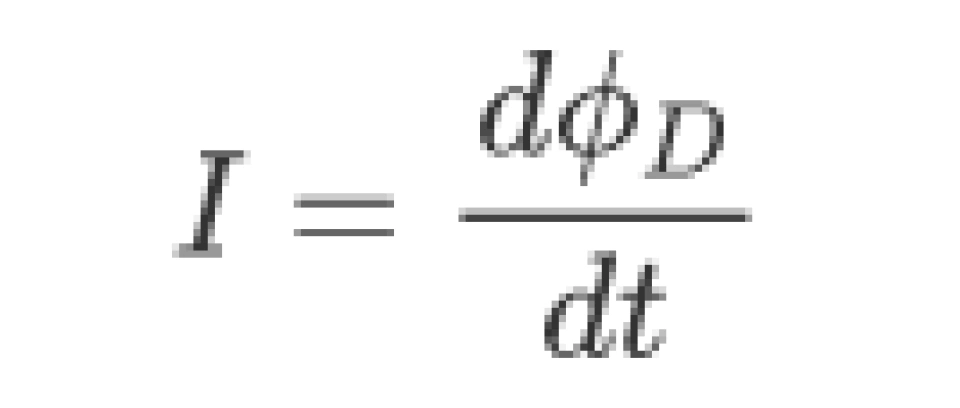
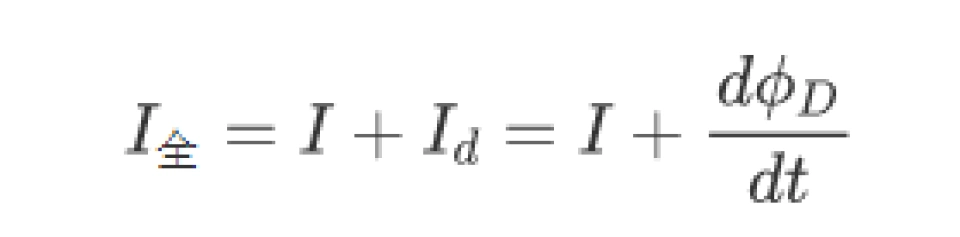
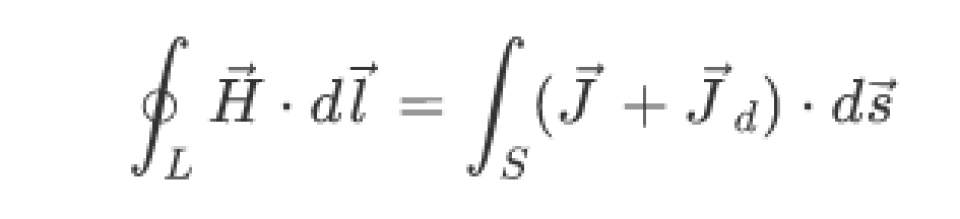

![[s-2]](https://www.bokeyuan.net/pic/image/emoji/cas/2.png)











