科普驿站 第五十三期
主题：时光机与任意门（第四期 下）
难度：B1-B2
讲师：弦轴子
物质的分布和运动决定了时空结构。知道物质分布和运动就可以知道时空结构。那么相类似地知道时空结构就可以反推出来物质的分布和运动，这一点在上面也提到过，我们可以先猜一个度规，再用场方程算能量动量张量，从而知道物质场的分布和运动情况。
对于研究虫洞，我们也是采用这个措施。
我们知道球对称可穿越虫洞的时空结构，我们就可以反推出来虫洞附近的物质分布和运动。
虫洞的度规是静态球对称的，这也给物质能量动量张量的形式施加了一定的限制， 使它在 t，r及两个横向坐标组成的正交标架场中具有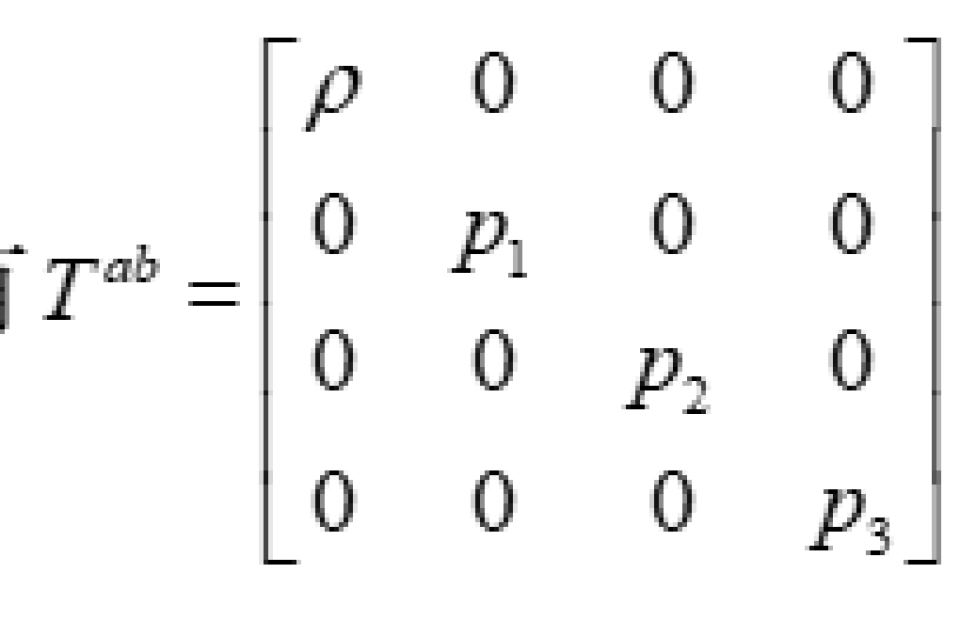
的正则形式。
标架就是说空间的定点 O ，连同三个不共面的有序向量 e1，e2，e3 的全体，叫做空间中的一个标架，记做 {O；e1，e2，e3}。如果e1，e2，e3 都是单位向量，那么 {O;e1，e2，e3} 就叫做笛卡儿标架。两两互相垂直的标架叫做笛卡儿直角标架。在一般情况下， {O;e1，e2，e3} 叫做仿射标架。当空间取定标架 {O;e1，e2，e3} 后，空间全体向量的集合或者全体点的集合与全体有序三数组 x，y，z 的集合具有一一对应的关系，这种一一对应的关系就叫做空间向量或点的一个坐标系。此时，向量或点关于标架{O;e1，e2，e3} 的坐标，也称为该向量或点关于由这标架所确定的坐标系的坐标。标架是空间坐标系的向量化。
正交标架场 (以下简称标架场) 由一组正交归一的基矢量场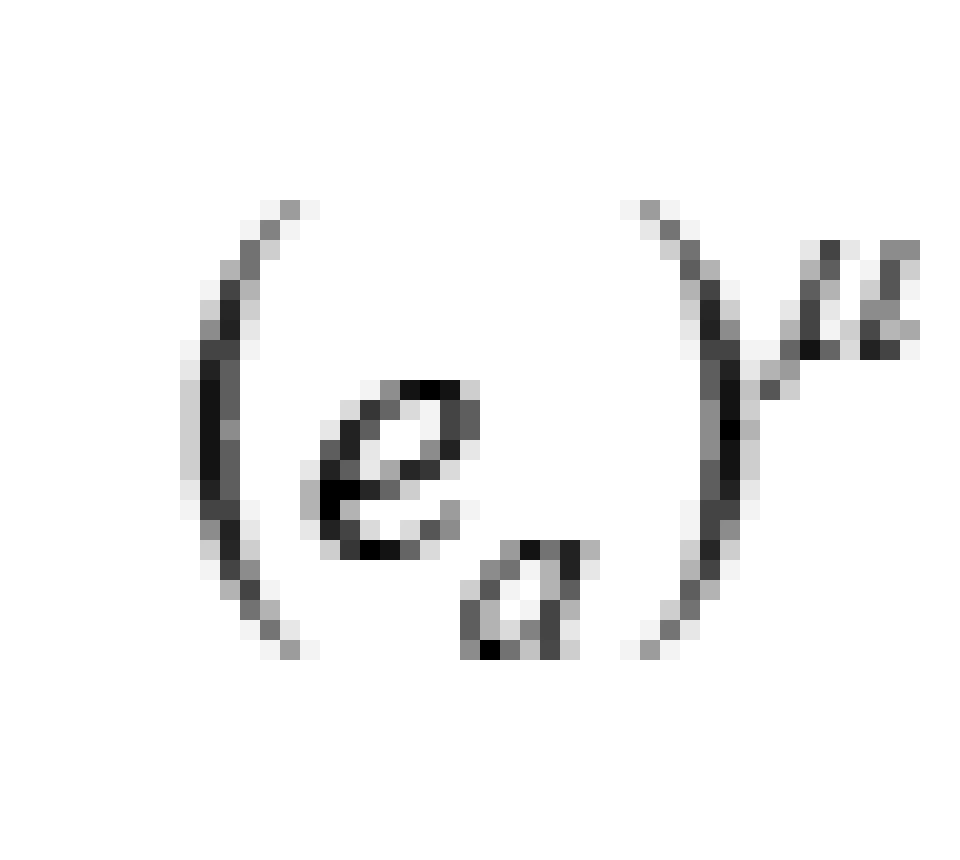
组成， 其中拉丁字母 a， b，…… 标识标架场的基矢量， 希腊字母 μ ，ν，…… 表示基矢量的时空指标。标架基矢
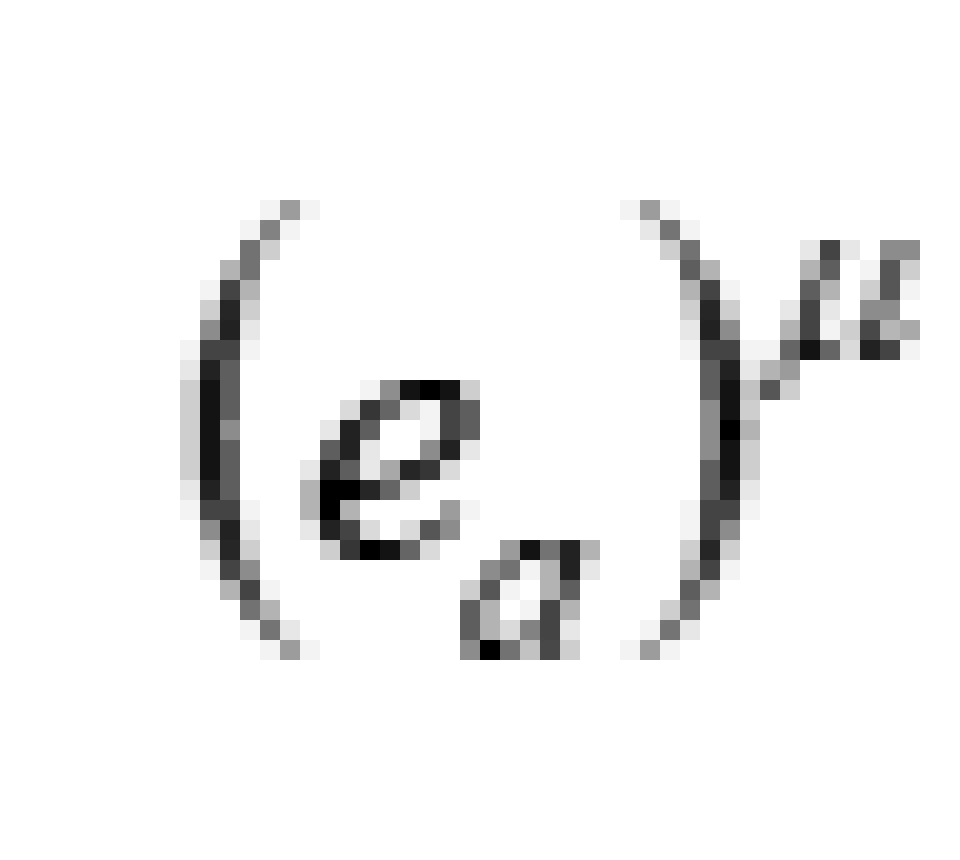是时空坐标的函数，因此叫做标架场。彼此又是正交，故名正交标架场。
而正则形式，其实说的就是张量的对角化。学过线性代数的朋友一定知道，就是主对角线的元素不为零，其他的都为0，而且也知道实对称张量必定可以通过正交变换对角化。
能量动量张量是实对称张量，一直都可以对角化。如果在广义相对论框架下，不能套用线性代数中的知识。原因在于普通线性代数所讨论的内积空间具有正定度规(也就是度规中的对角元素全是正的)，而广义相对论中的时空度规不是正定的(也就是度规张量中的对角元素有正有负)。
其中 ρ 是能量密度，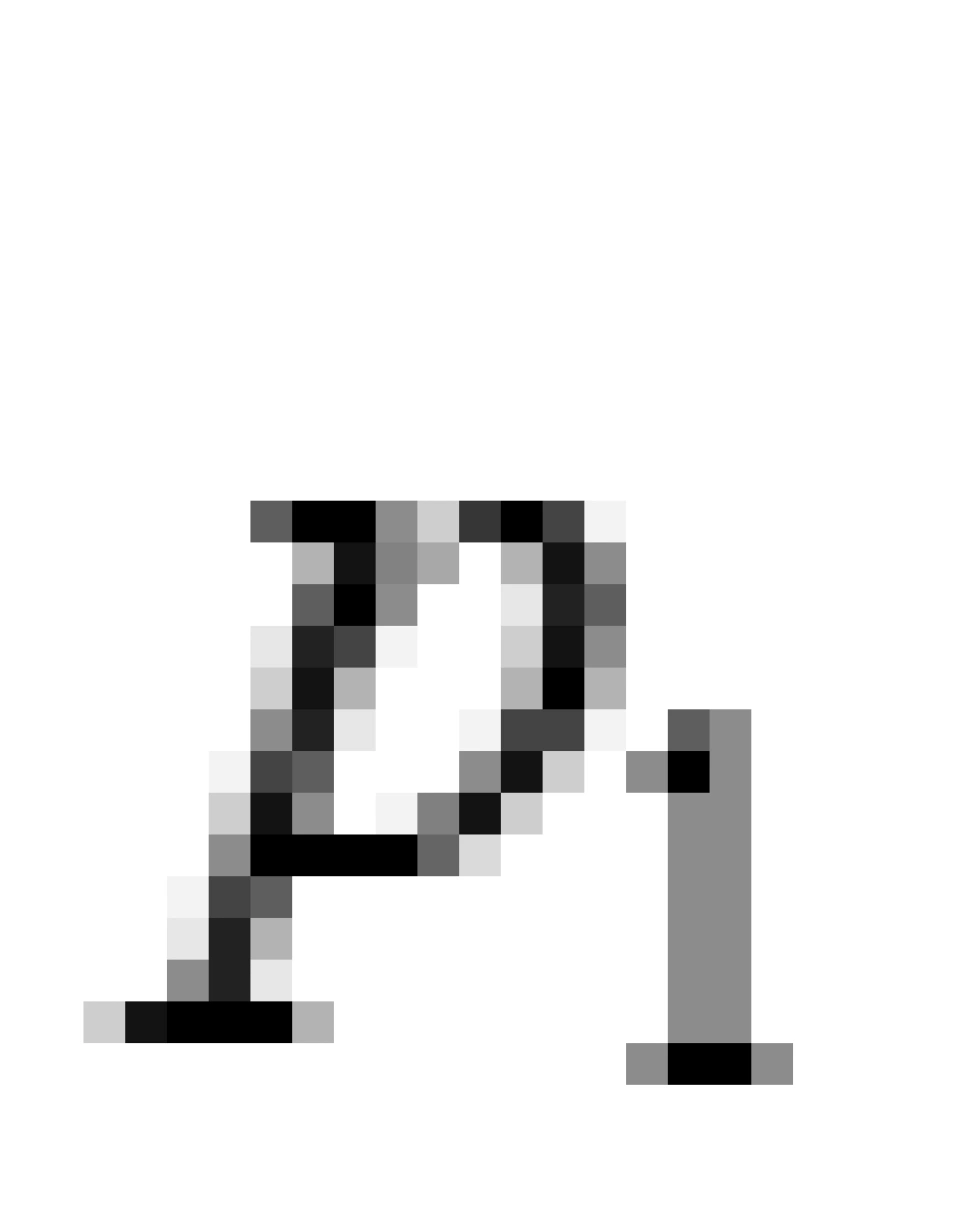
是径向张力，
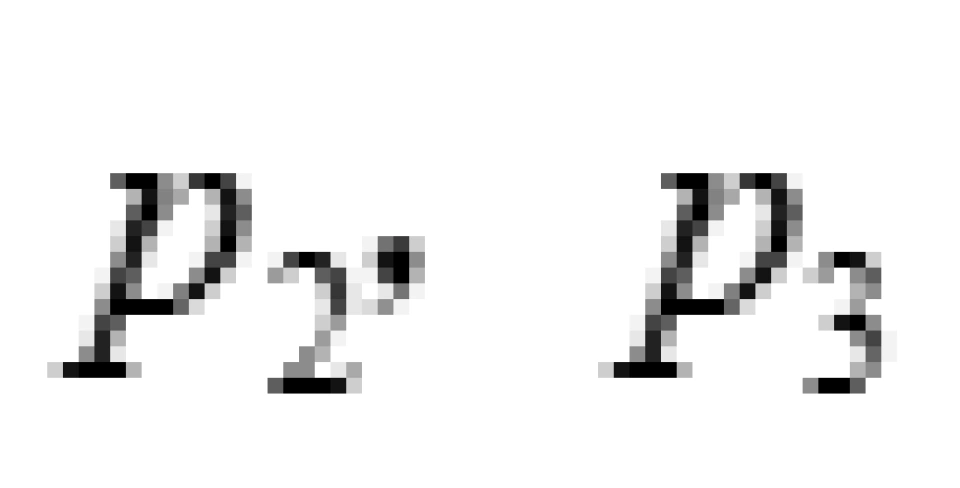是横向压强，它们都只是径向坐标r的函数。 这就是球对称可穿越虫洞的物质分布所需满足的一般条件。
最终我们得到一个式子：
这是什么意思呢？为了看懂这个式子，我们是还要介绍一个内容。那就是能量条件。
爱因斯坦场方程的精确解一般套路就是设度规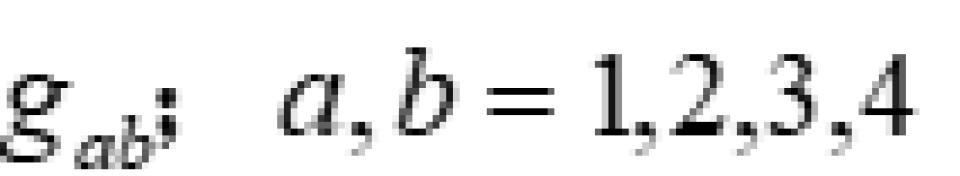
为任意的度规，从而计算出来爱因斯坦张量
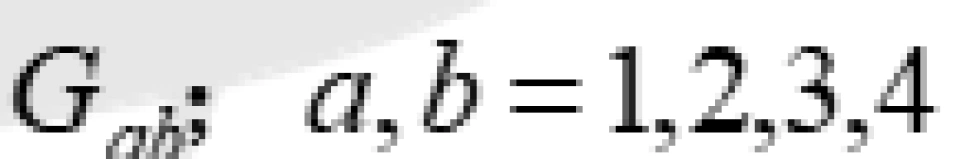。确定了方程左边就可以知道右边
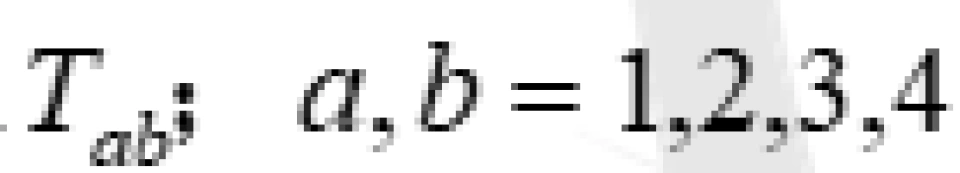。它是描述物质分布和运动的能量动量张量，代表的是描述某种物质场分布。不过在实际宇宙中情况是很复杂的，物质的分布往往不是单一的，因此能量动量张量受大量不同物质的影响。在这个限制下，如果想精确每一处能量动量张量几乎是不可能的事情。但是只要我们可以给出能量动量张量的一些限制，一些条件，就可以做到。
这些条件被称为能量条件。一共有4种条件，但是这里我们只讲三种。
第1个条件是弱能量条件：
要求任意一个瞬时观察者所测得的能量密度必须是非负的，也就是他们不可能观察到负能量的情况出现。
数学形式就是：
，其中，
都是类时的。
利用正则形式
；
是空间上三个方向的主压强。
我们可以证明：弱能量条件等价于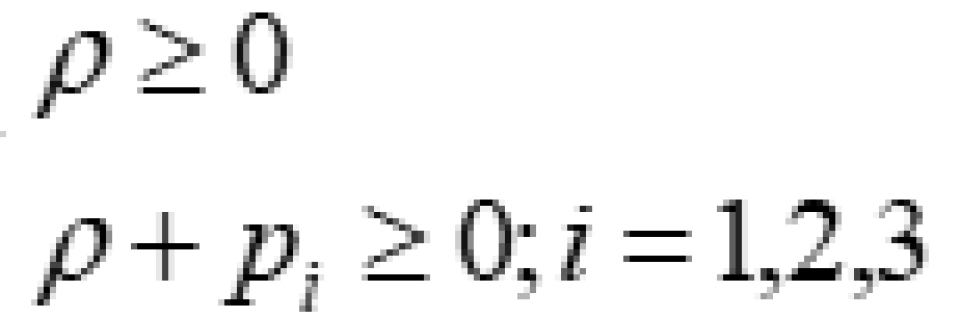
。
第2个条件是强能量条件：
要求瞬时观察者所观察到的压强可以是负的，但是不能太负。
有一个限制，负压强的绝对值不会大到使得 
。
最终数学形式是：
；其中，
为单位类时向量。
第3个条件是主能量条件：
要求任意的瞬时观察者所测量的四维动量密度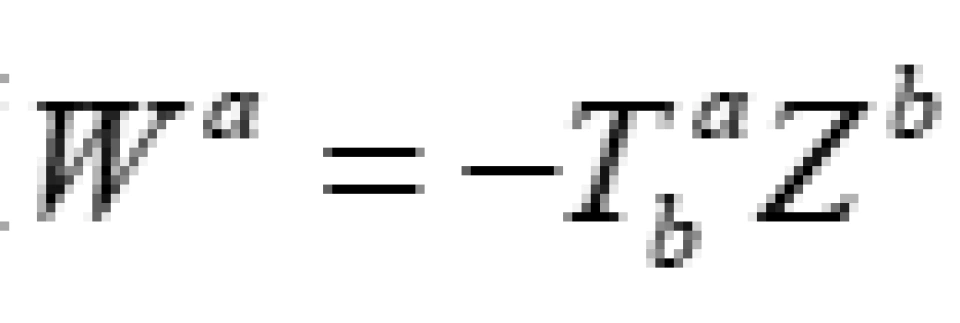
必须是未来类时或者未来类光的，简单来说就是物质场之间的能量流动速度必须小于光速，能量传递的速度必须小于光速。
让我们回到正轨，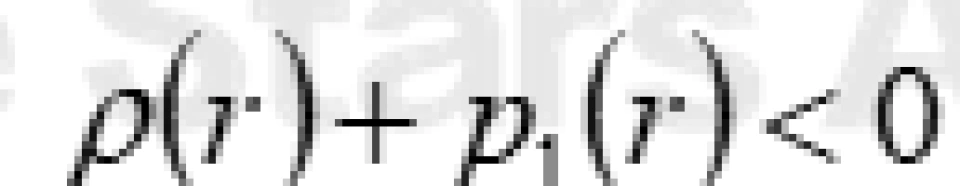
，这个式子是维持虫洞结构稳定的物质分布的。
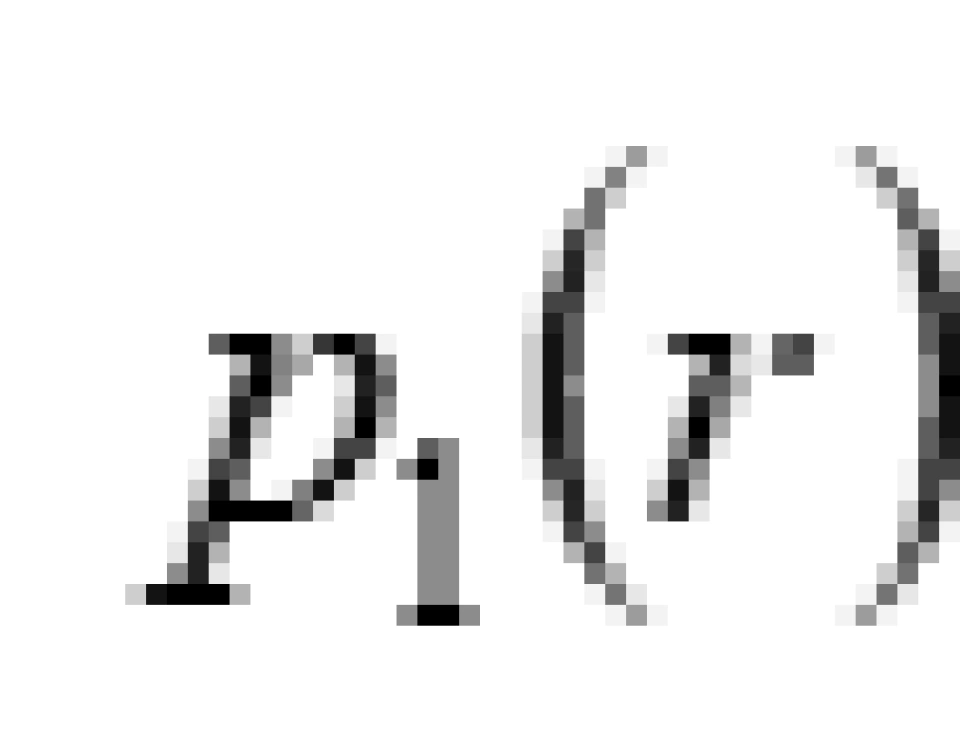是空间上某个方向的主压强。
弱能量条件
，但是维持虫洞结构稳定就必须要求
。
这意味着，虫洞附近必须存在负能量密度才可以维持稳定。
因此，如果想建造可穿越的虫洞，就必须有大量的负能量密度物质维持结构才可以。
当然这样的虫洞仅仅是为了省距离，穿越时间必须要求两个洞口的时间不一样。
这个很好做，因为两个洞口是平直时空。只要高速运动或者在附近构建一个引力场就可以。
而且上面我们也说了两个洞口的质量也可以不一样。
因此，它们实际的时间流速也可以不一样，这样就可以利用时间差进行时空旅行。
不过这种方法，不可能穿越到虫洞建造之前，尽管是两个洞口，但是因为引力时空膨胀效应还是双生子效应，所产生的时间差或者是穿越时空都是微乎其微的，所以几乎不可能回到虫洞出现之前。
最后，前三期关于“虫洞”方面的相关知识就告一段落了。从接下来的第四期开始，我们将开始介绍有关“哥德尔宇宙”理论模型的相关知识。
参考引源：
《广义相对论基本》，赵峥，刘文彪
《广义相对论》，刘辽，赵峥
《黑洞与弯曲的时空》，赵峥
《微分几何入门与广义相对论》上中下册，梁灿彬
【本文为耀星会的原创作品，未经允许，禁止盗用、转载、篡改文章，否则耀星会和作者将追究版权责任。】
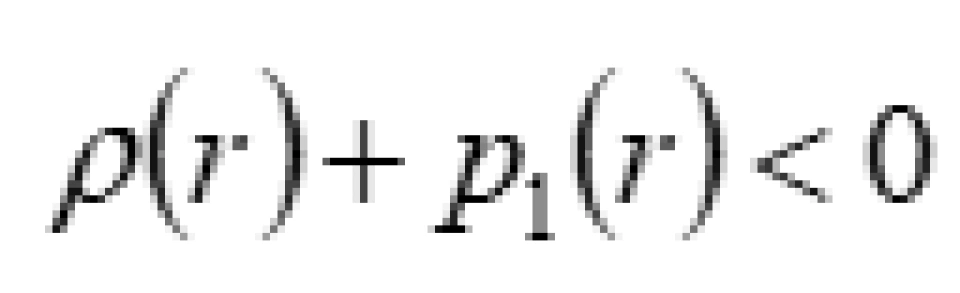
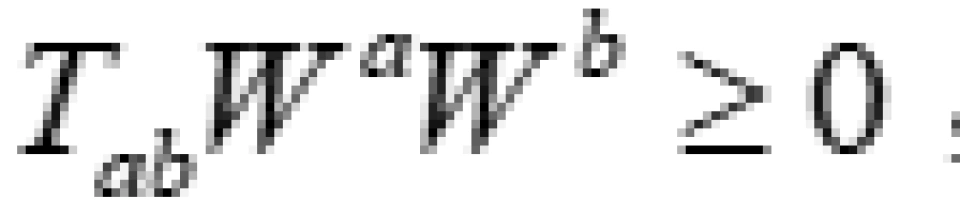
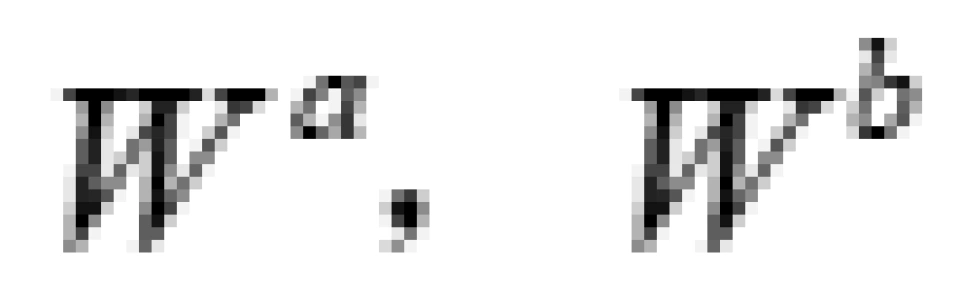
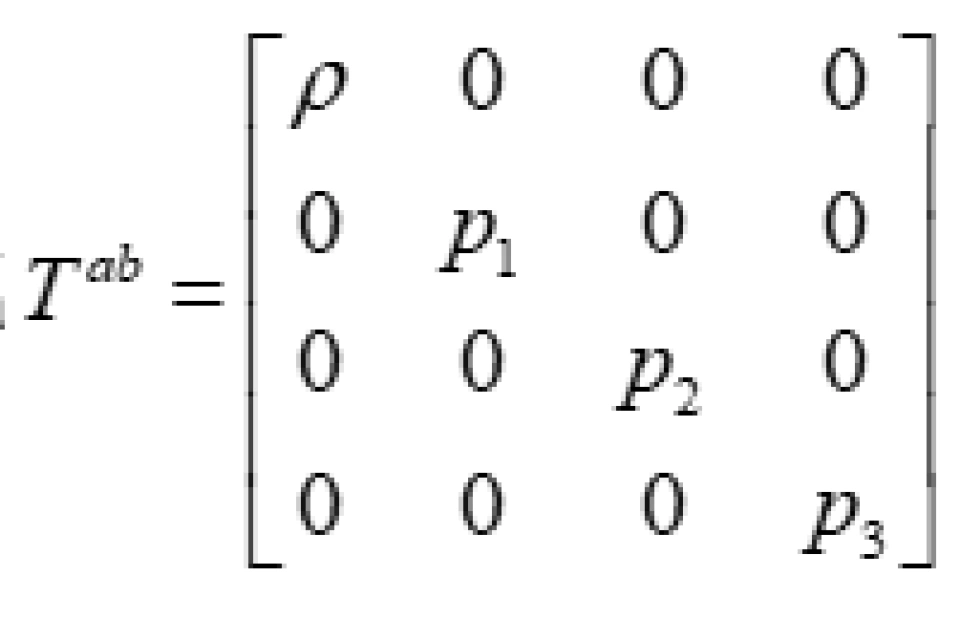
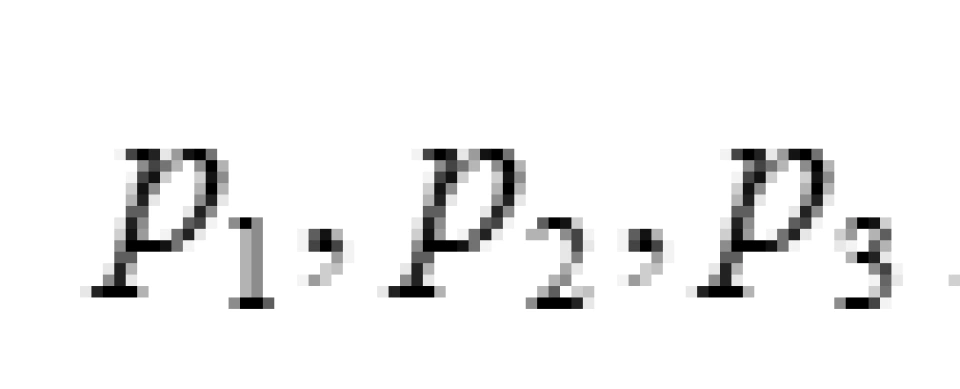
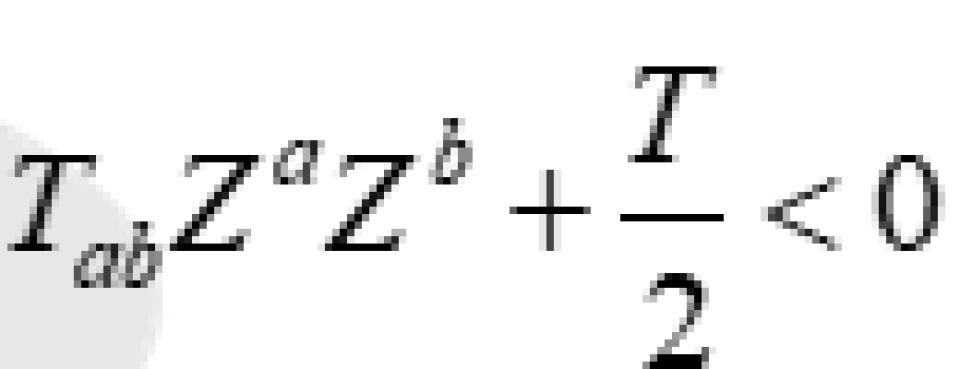
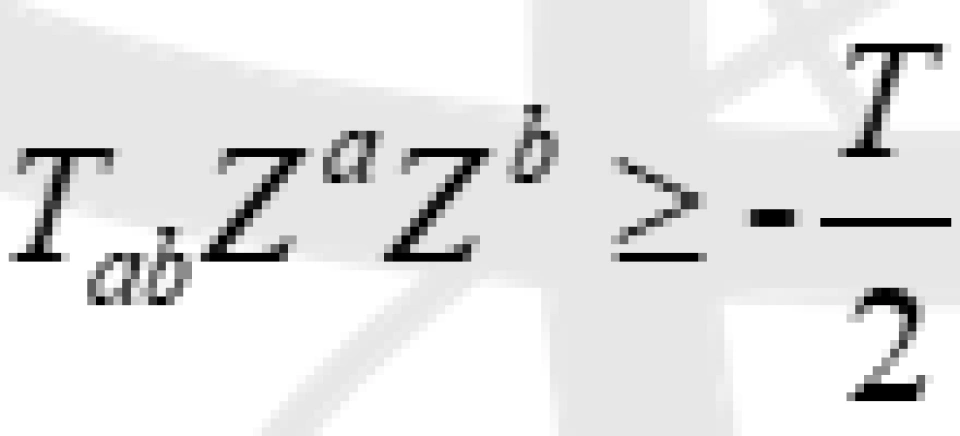
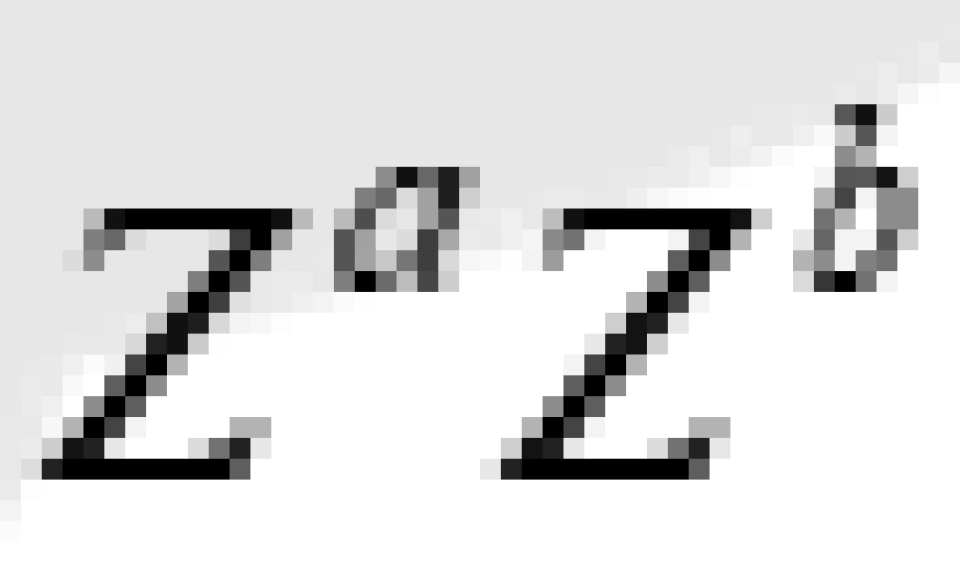
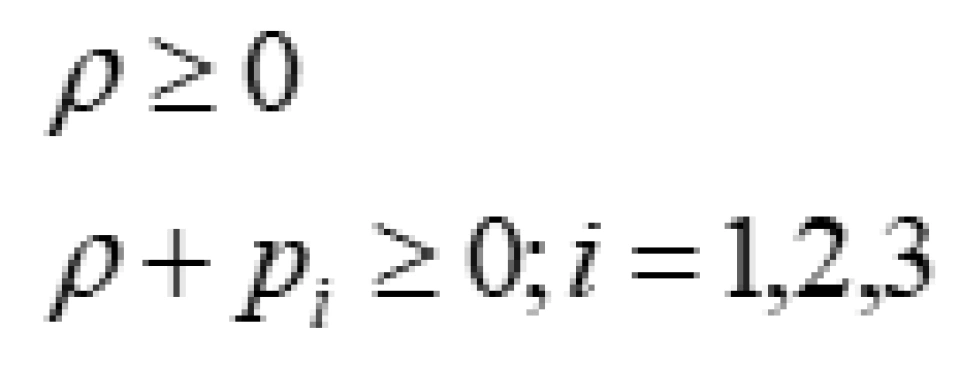
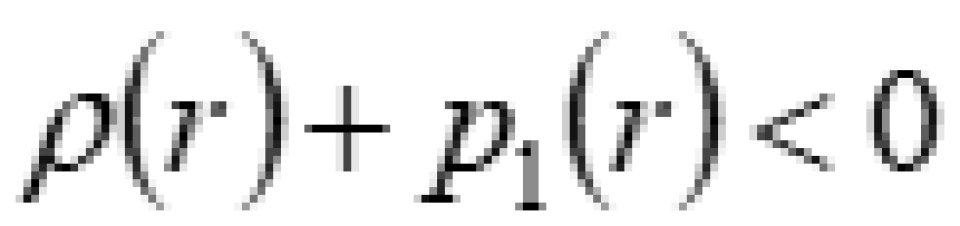
![[s-70]](https://www.bokeyuan.net/pic/image/emoji/cas/70.png)
![[s-1]](https://www.bokeyuan.net/pic/image/emoji/cas/1.png)
