科普驿站 第五十三期
主题:时光机与任意门(第四期 上)
难度:B1-B2
讲师:弦轴子
1.不存在视界,因为视界是单向膜,穿过去就不可能往返。比如上面我们介绍的克尔黑洞,它的内部理论上存在的可穿越的虫洞,不过很可惜,这个虫洞包裹在克尔黑洞的视界内。一旦想利用这个虫洞,就要闯入视界内部,一去不复返,再也无法跟自己所处的外部宇宙相联系。因此,一个合格的可穿越虫洞就必须不存在视界。
2.穿越过程中遇到的应力是人体能够承受的。这个显而易见,要不然被人撕碎了,穿越也就没有意义了。
3.满足广义相对论场方程。毕竟在这个框架内讨论的,肯定符合这个框架的基本方程。我们希望能够通过这个方程解出虫洞解。
4.在微扰下保持稳定。从上面对于克尔黑洞内部虫洞的讨论可以知道,目前认为进一步的计算有可能表明克尔黑洞内部虫洞在通过类时线这种真空微扰的作用下变成只能通过类光线。因此在某种微扰下,虫洞必须保持稳定,包括不会坍塌和保持结构稳定。
5.出入口分别连接渐近平直时空。这个也显而易见,毕竟我们要从洞口进入,而我们生活宇宙就是平直时空。
上述这些可穿越虫洞所需满足的基本条件与当年基普所考虑的条件也差不多,不过他们为了方便研究,还增加了两个。
6.虫洞的度规是静态球对称的。
7.虫洞的“喉咙” 是唯一的。
因此,他根据这些条件构造出来了虫洞的度规:
其中,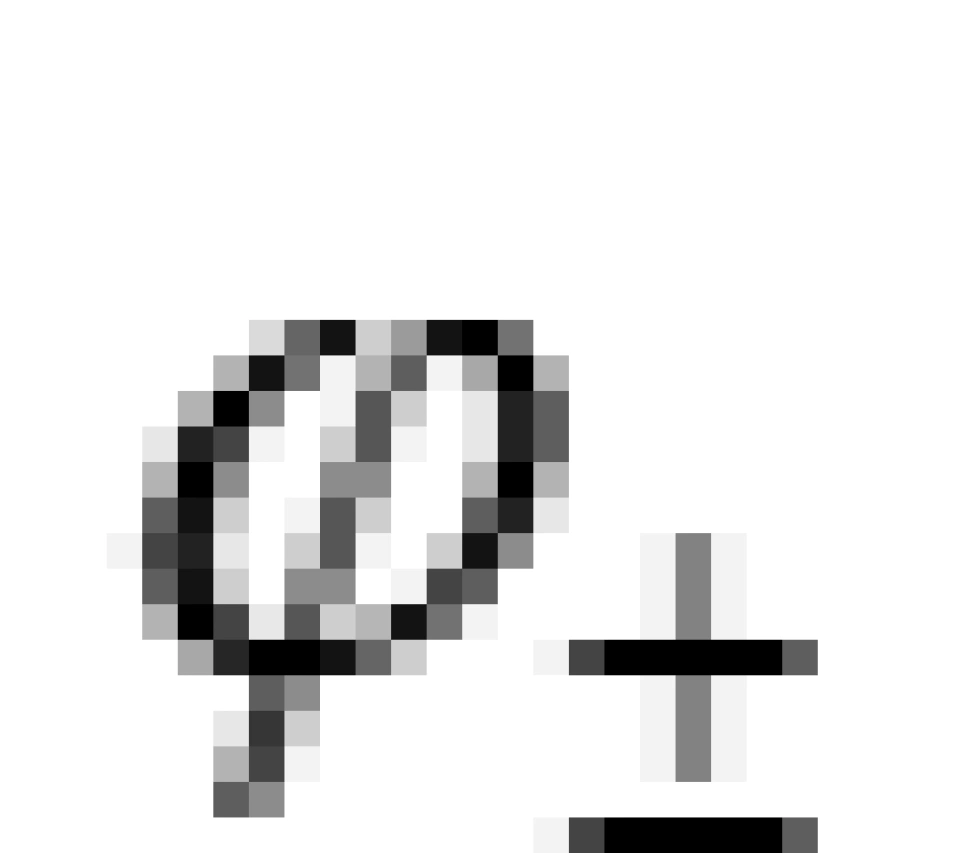 和
和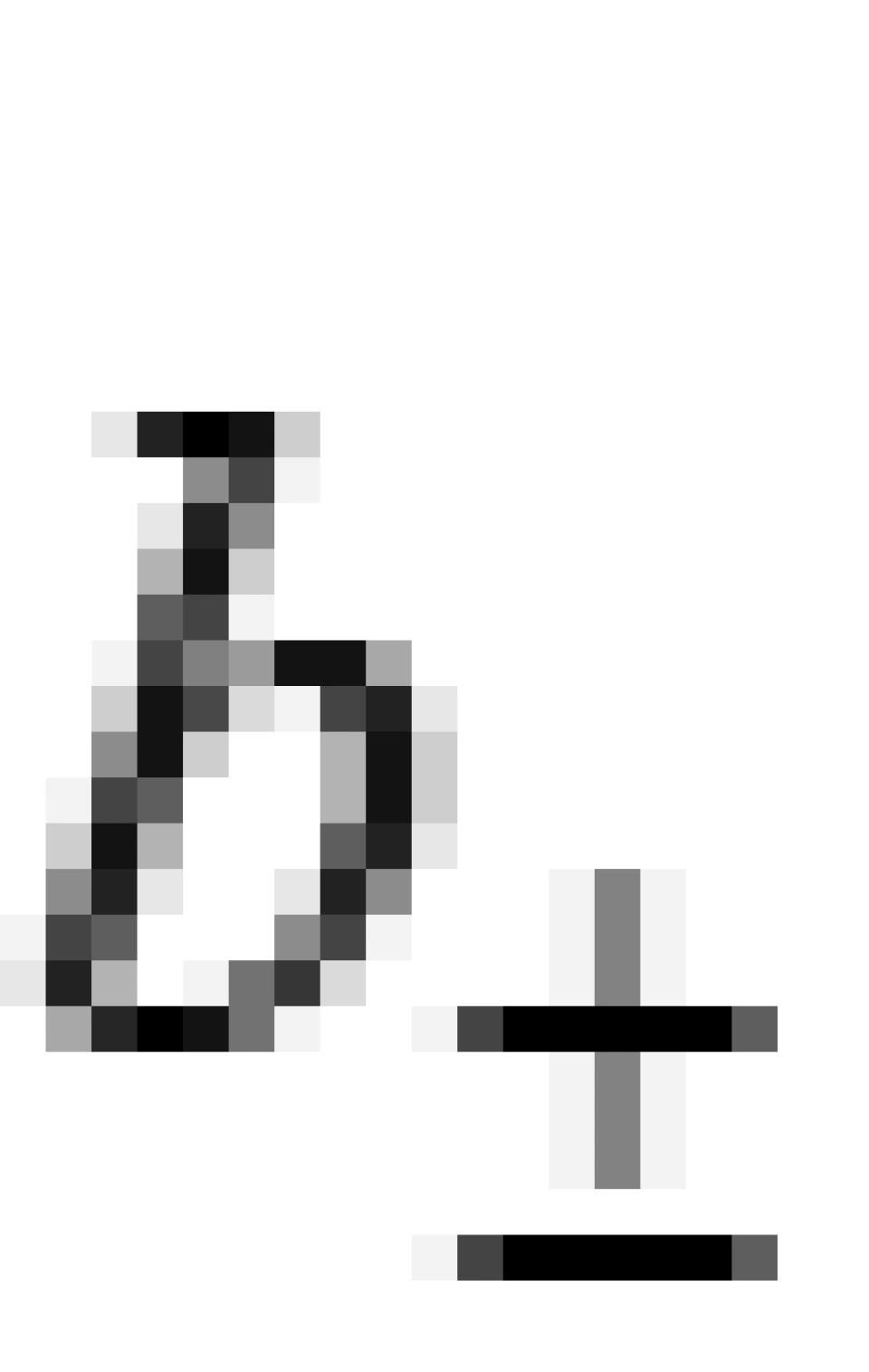 的下标
的下标 分别表示两个坐标域,而这里的坐标域的引入来源于第5个条件:虫洞出入口分别连接着渐近平直时空。
分别表示两个坐标域,而这里的坐标域的引入来源于第5个条件:虫洞出入口分别连接着渐近平直时空。
因此,我们引进两个坐标域来分别描述出口和入口附近的时空,两者在 “喉咙” 处相互衔接。它们是关于r的函数。
我们知道,第7个条件说的是虫洞的度规是静态球对称的。而众所周知,度规是静态球对称的,一般形式是包含两个任意函数,且两者都只是径向坐标r的函数。
因为静态球对称度规对应的是静态球对称真空解,它对应的就是只存在于球对称引力源外部的不随时间变化的引力场。
我们都知道,在广义相对论的框架中,物质的分布和运动影响时空结构,引力是时空结构的弯曲的几何表象,用度规张量描述。引力场的物理效果可通过黎曼几何中的几何量——度规张量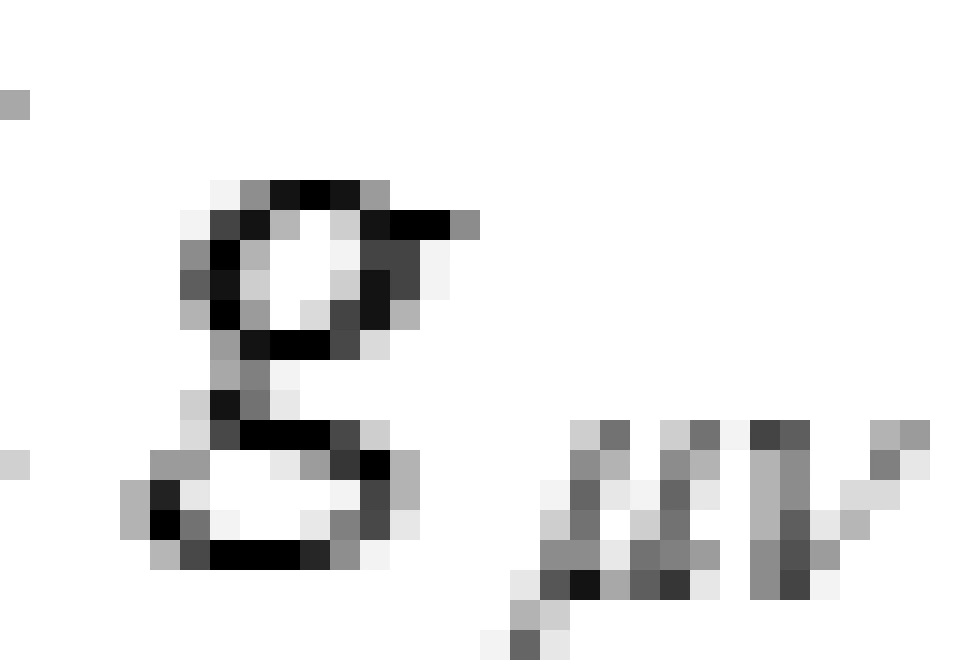 来体现。而物质的分布和运动用一个二阶张量来描述,那就是能量动量张量。它是一个4×4的矩阵,有16个分量,包含能量流,动量流,能量密度还有三维空间中各个方向的应力/压强。
来体现。而物质的分布和运动用一个二阶张量来描述,那就是能量动量张量。它是一个4×4的矩阵,有16个分量,包含能量流,动量流,能量密度还有三维空间中各个方向的应力/压强。
因此,描述引力相互作用的爱因斯坦引力场场方程的一端是描述物质场运动和分布的能量动量张量,另一端是反映时空结构变化的张量,而且以度规张量为函数。具体推导过程就不说了,直接写出爱因斯坦场方程。
爱因斯坦引力场场方程其实就是:
曲率项=物质项
其中: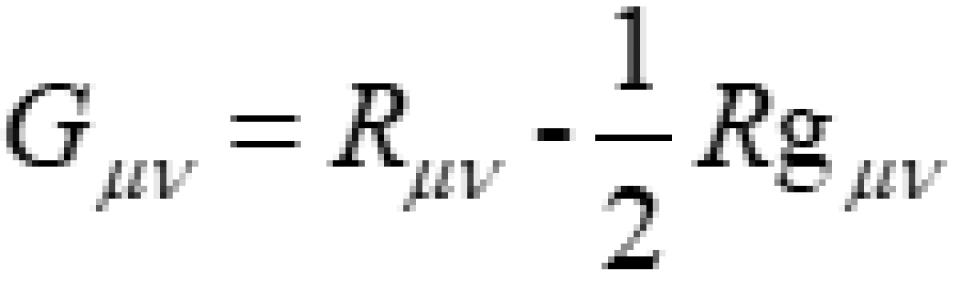 ,这里每个都是4×4矩阵,有16个分量,它们是对称张量,k为系数,
,这里每个都是4×4矩阵,有16个分量,它们是对称张量,k为系数, 是描述物质上的分布和运动的能量动量张量。
是描述物质上的分布和运动的能量动量张量。 被称为里奇张量,它是由四维黎曼曲率张量
被称为里奇张量,它是由四维黎曼曲率张量 缩并而来的,即:
缩并而来的,即: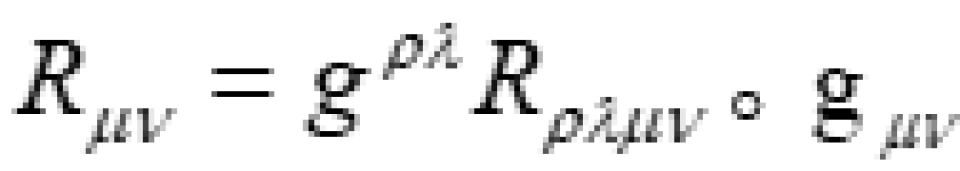 就是我们前面说的度规张量,而R它叫做曲率标量,是由里奇张量缩并而来的亦即:
就是我们前面说的度规张量,而R它叫做曲率标量,是由里奇张量缩并而来的亦即: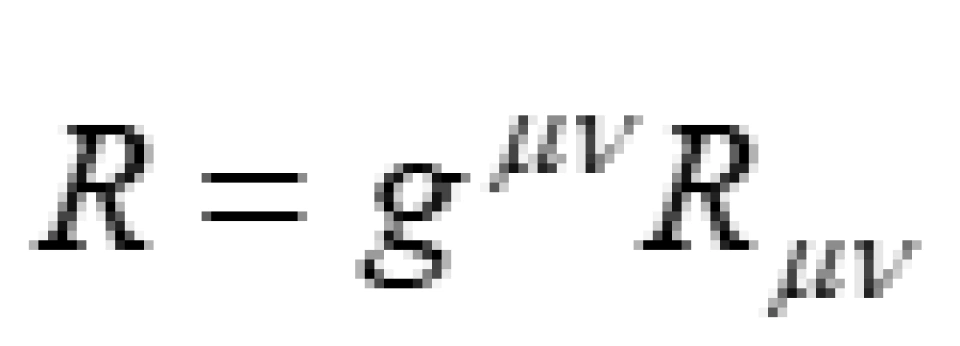 。
。
张量缩并可以当做是一种矩阵求迹的扩展。一个二阶张量的分量用矩阵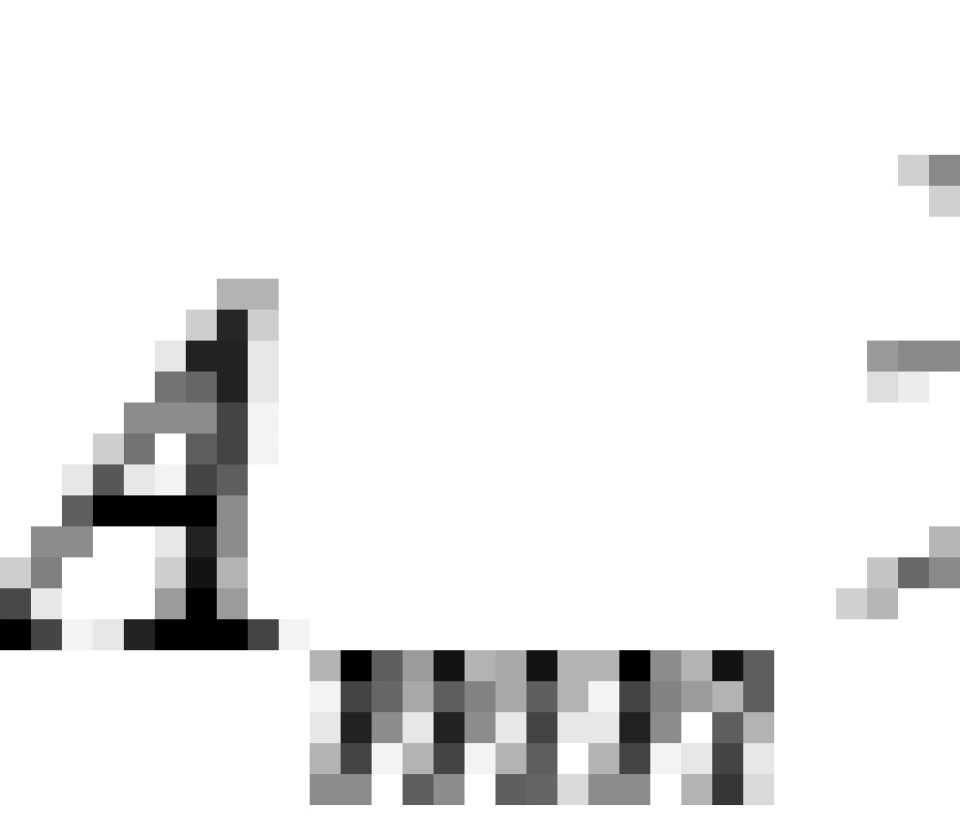 表示,当m=n时,只剩下对角线上元素,所有对角线上元素的和就是迹,亦即是缩并为一个标量。迹,只在二阶张量也就是矩阵上有定义,它在高阶张量上的推广就是张量的缩并。
表示,当m=n时,只剩下对角线上元素,所有对角线上元素的和就是迹,亦即是缩并为一个标量。迹,只在二阶张量也就是矩阵上有定义,它在高阶张量上的推广就是张量的缩并。
其实也不难理解,因为张量本身就是矩阵的高阶扩展。三阶张量缩并就是一个矢量,缩并后降两阶。
引力场的分布在广义相对论框架中,其实就是与度规场的分布有关。度规场其实是关于度规的一套分布函数,但该函数是由爱因斯坦场方程来确定的,由爱因斯坦场方程直接求出度规的分布函数,不能直接求出某时空点的度规。所以首先是由场方程接出对应的度规场函数,然后才能得到某点的度规。
当然有的时候爱因斯坦场方程很难求解(精确解)(万一考虑的外界条件不是球对称),因为广义相对论场方程也就是爱因斯坦引力场场方程是由10个二阶非线性偏微分方程构成的方程组,用以确定10个决定时空几何性质的未知函数,也就是度规张量的10个独立分量。度规张量是4×4矩阵,一共有16个分量,但是由于度规张量是对称性的,因此,最后只有10个独立分量。它们对应着10个二阶非线性偏微分方程。这个方程组内还有4个恒等式,因此真正有用的独立方程只有6个。不过要想解方程,还必须引入4个跟坐标系选择有关系的微分方程,被称为坐标条件。这样加起来独立方程还是10个。十个方程,十个未知函数,十个独立分量正好匹配。不过,如果想真正解微分方程,还必须有初始条件和边界条件。因此实际上去求解爱因斯坦引力场场方程是一件很困难的事情。
所以最后只有十个是独立分量。因此,这个方程实际上是十个联立的二阶非线性偏微分方程(度规张量的10个独立分量),实际上很难解。
但是,我们可以反操作,先猜出一个解,然后再带入方程,得到我们想要的信息。
具体操作是:这个时候可以猜出来一个度规,再用场方程算能量动量张量,这样肯定是精确解,只不过无法保证求出的能量动量张量在我们宇宙中是真实存在的。
解爱因斯坦场方程其实就是在求解度规场的分布函数。如果我们假定引力源是球对称性的,然后求解引力源外部的度规场,引力源外部的时空区自然就是真空。
从对称性的角度考虑,如果我们假设物质的分布(引力源)是球对称的,真空区(引力源外部区域)也应该是球对称性的,所以如果我们采用球坐标系,那么一般的真空球对称性度规应该可以写成这样:
不难看出,包含两个任意函数,且两者都只是径向坐标r与t的函数。
根据伯克霍夫定理:(真空球对称度规一定是静态的)真空球对称度规,应该是写成与时间无关的形式。
因此,我们可以得出一个结论:度规是静态球对称性的,一般形式是包含两个任意函数,且两者都只是径向坐标r的函数。
那我们回归主旨,看看虫洞的度规。
坐标r的取值范围是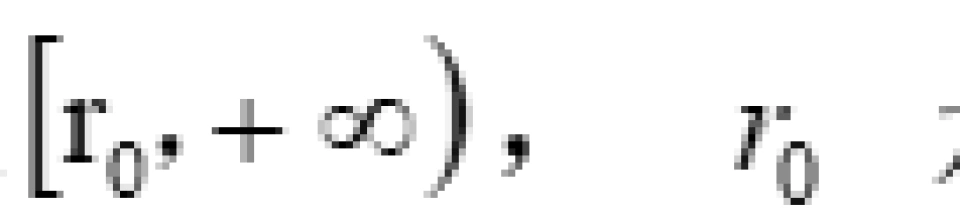 是 “喉咙” 所对应的径向坐标值。而虫洞度规是静态球对称性的,一般形式是包含两个任意函数,且两者都只是径向坐标r的函数。
是 “喉咙” 所对应的径向坐标值。而虫洞度规是静态球对称性的,一般形式是包含两个任意函数,且两者都只是径向坐标r的函数。
广义相对论场方程是二阶偏微分方程。因此,我们根据第3个要求,要求 起码是二次可微的。
起码是二次可微的。
我们根据第1个要求,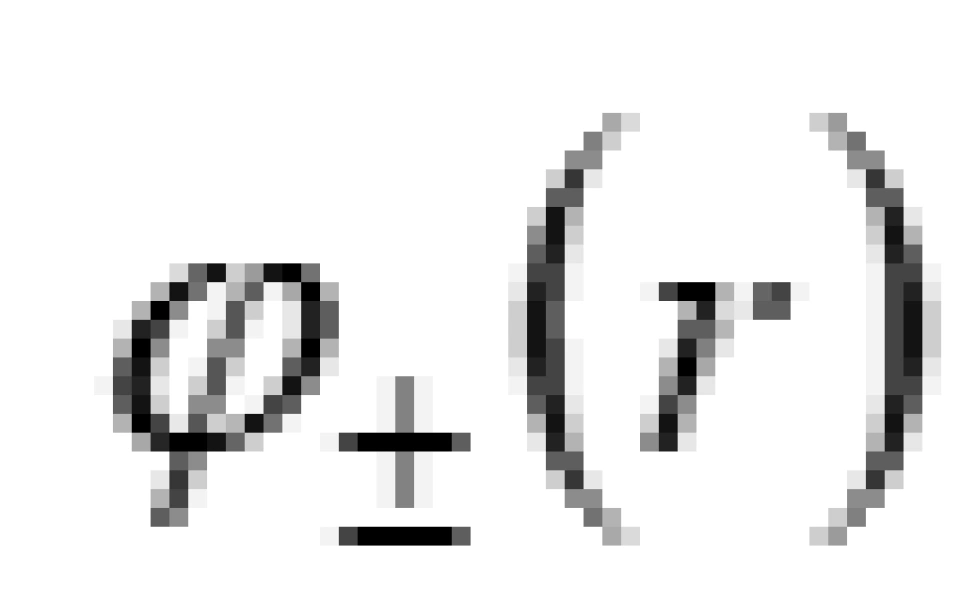 是处处有限,这样就不会存在视界。这样的话,
是处处有限,这样就不会存在视界。这样的话,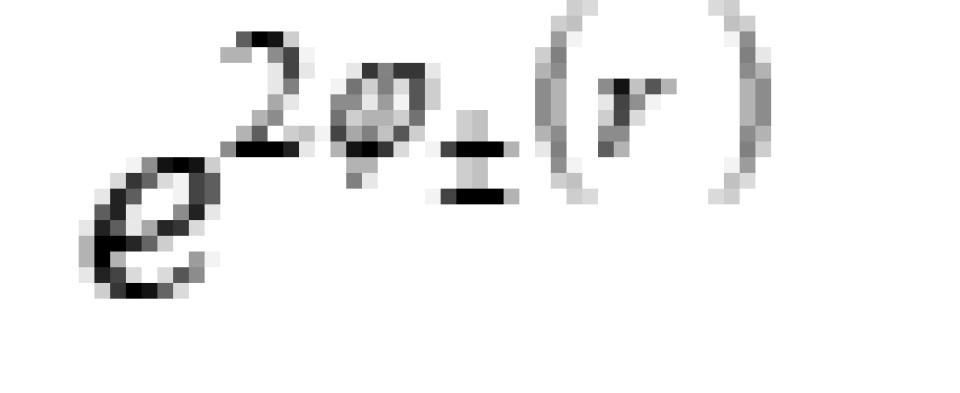 不会像其它度规那样在某些地方为零亦即存在事件视界。
不会像其它度规那样在某些地方为零亦即存在事件视界。
除上述一般限定外, 这一度规在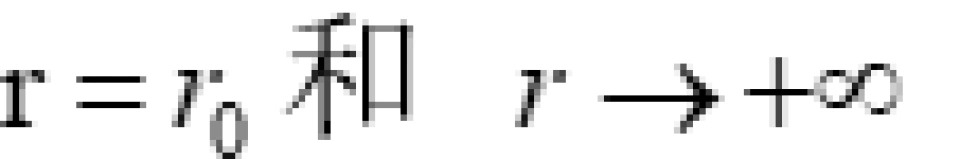 需要满足一些边界条件。 对于
需要满足一些边界条件。 对于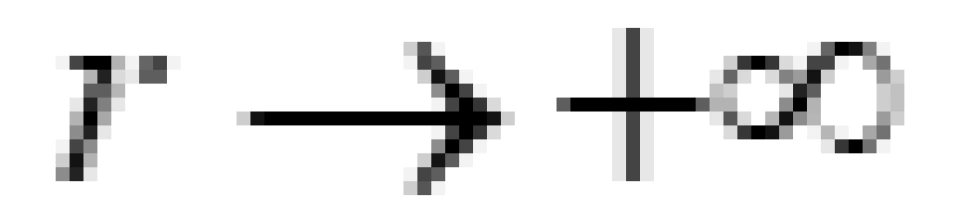 , 由于出入口连接渐近平直时空 (条件9), 因此
, 由于出入口连接渐近平直时空 (条件9), 因此  均为 (有限) 常数。 在一般情况下, 这两个常数可以是不相等的。同样的,
均为 (有限) 常数。 在一般情况下, 这两个常数可以是不相等的。同样的, 也均为 (有限) 常数。
也均为 (有限) 常数。
与史瓦西度规相对比
不难看出,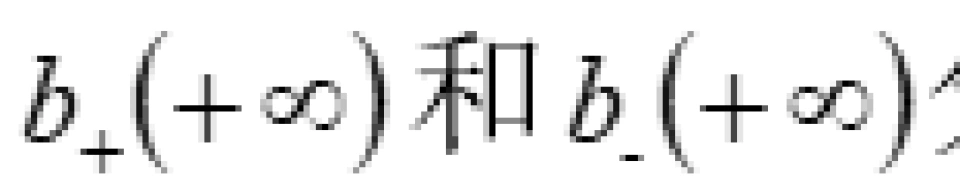 分别对应于在出入口所连接的渐近平直时空中测得的出入口,也称为洞口的质量 (确切地说是质量的两倍)。 一般来说,这两个常数也可以是不相等的, 即虫洞的两个洞口的质量可以是不相等的。
分别对应于在出入口所连接的渐近平直时空中测得的出入口,也称为洞口的质量 (确切地说是质量的两倍)。 一般来说,这两个常数也可以是不相等的, 即虫洞的两个洞口的质量可以是不相等的。
对于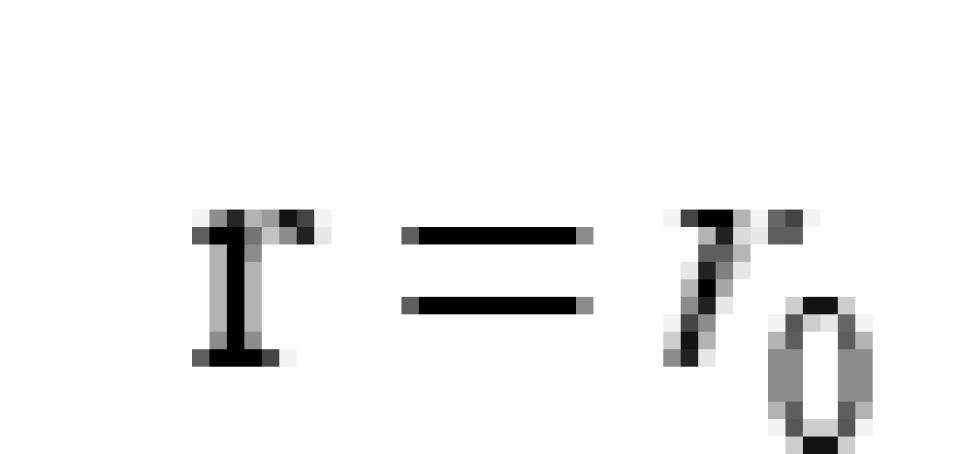 (即 “喉咙” 处), 由于两个坐标域在此衔接, 且
(即 “喉咙” 处), 由于两个坐标域在此衔接, 且  起码是二次可微的。因此,我们有:
起码是二次可微的。因此,我们有:
不仅如此,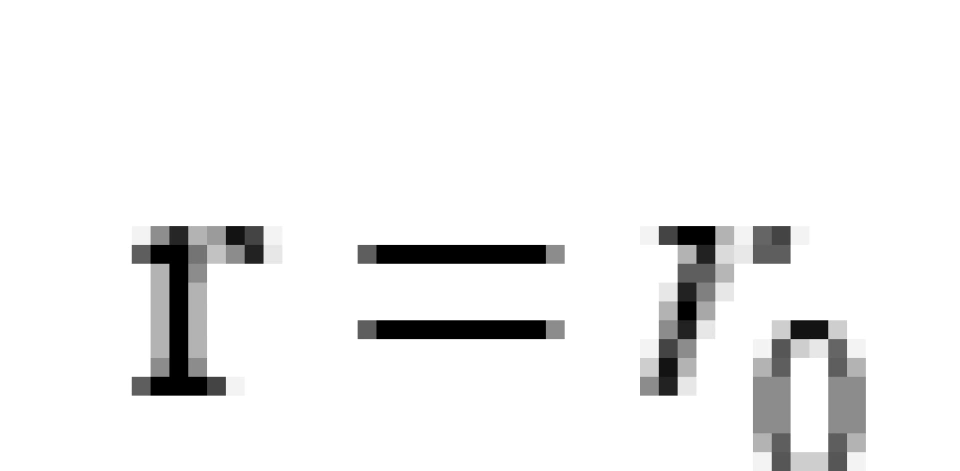 作为虫洞的 “喉咙”, 是径向坐标取值最小的地方。
作为虫洞的 “喉咙”, 是径向坐标取值最小的地方。
这表明:
由于 “喉咙” 是唯一的 (条件 8),因此在偏离但靠近 “喉咙” 的一个开区间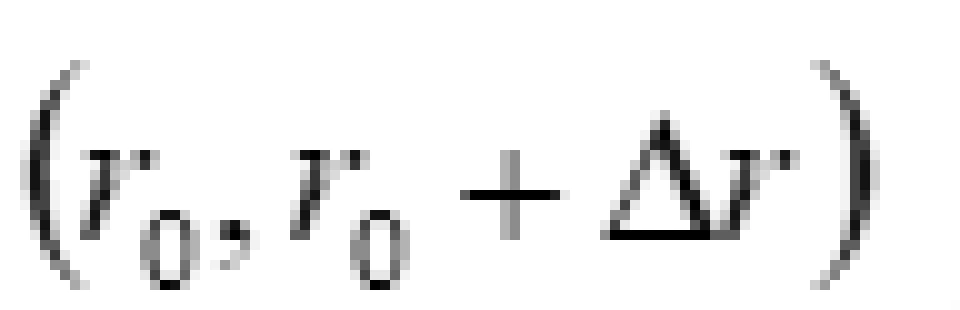 内:
内:
以上就是球对称可穿越虫洞的时空结构所需满足的一般条件。
参考引源:
《广义相对论基本》,赵峥,刘文彪
《广义相对论》,刘辽,赵峥
《黑洞与弯曲的时空》,赵峥
《微分几何入门与广义相对论》上中下册,梁灿彬
【本文为耀星会的原创作品,未经允许,禁止盗用、转载、篡改文章,否则耀星会和作者将追究版权责任。】


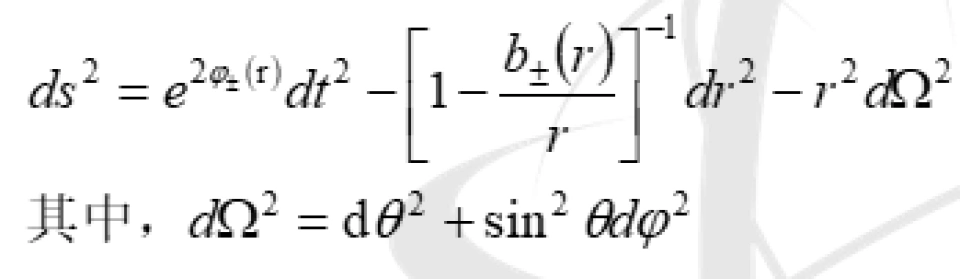
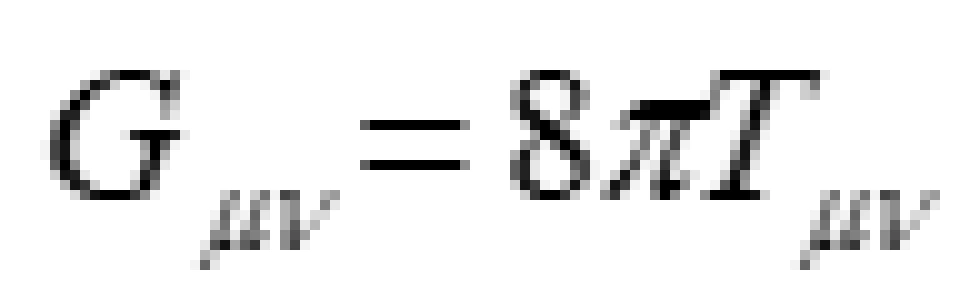
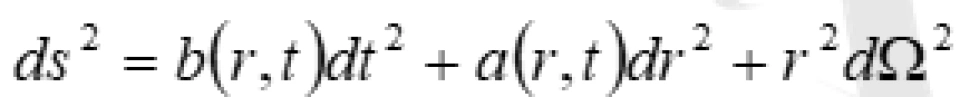
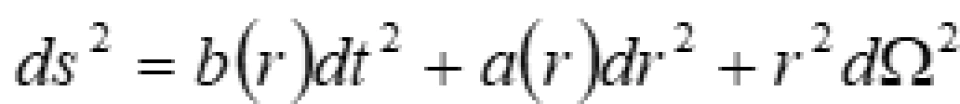
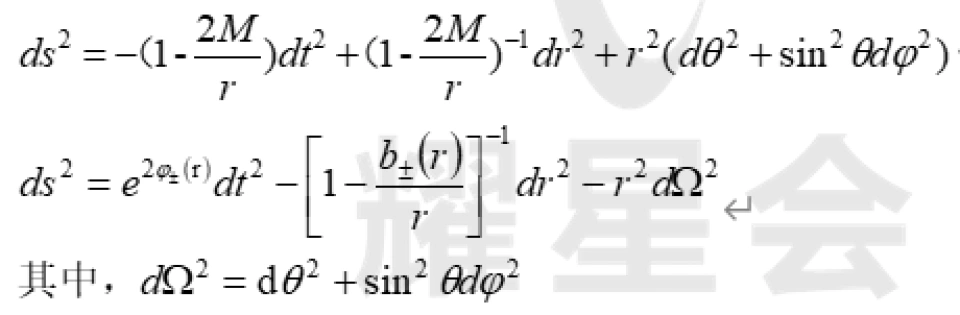
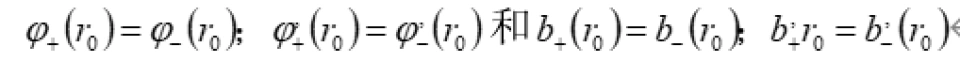
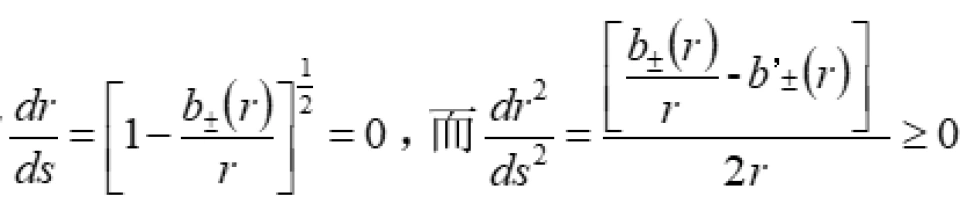
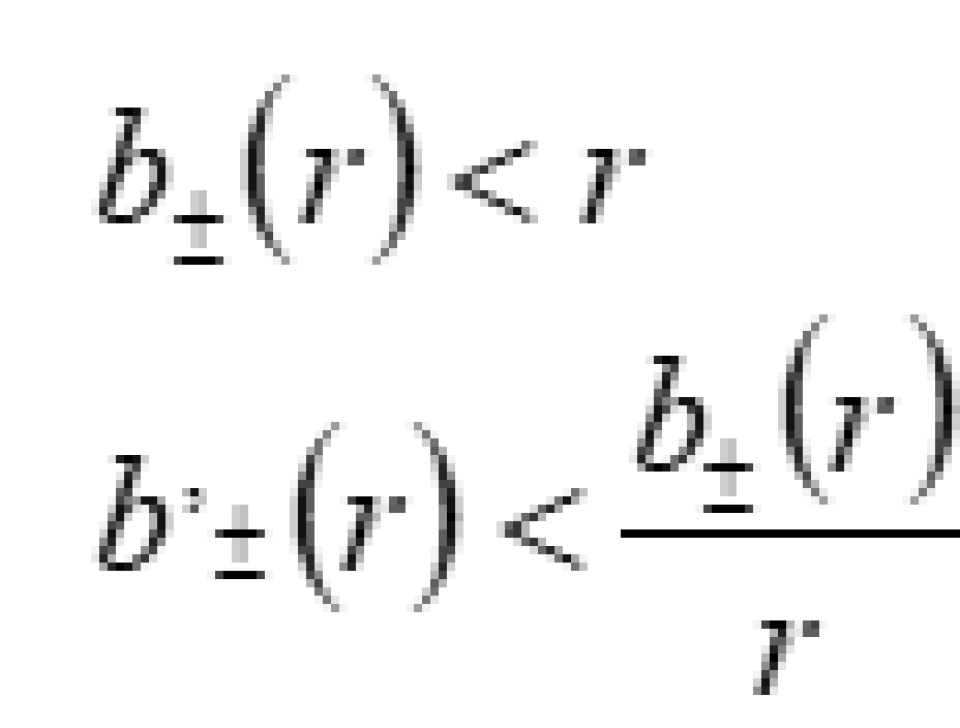

![[s-1]](https://www.bokeyuan.net/pic/image/emoji/cas/1.png)











