科普驿站 第51期
科目:物理
难度:B2
讲师:咕咕叶
自1900年普朗克提出量子概念至今已经过去了一百余年。这期间,经过爱因斯坦、玻尔、德布罗意、玻恩、海森伯、薛定谔、狄拉克等众多物理大师的努力与探索,到20世纪30年代已经构建成了一套完整的量子力学理论体系。这一理论是关于微观世界的理论,与支配宏观的相对论一起成为了现代物理学的理论基础。
物理量引用符号说明:
M_ν(光谱辐射出射度);
ν(频率);
h(普朗克常量);
m(质量);
p(动量);
E(能量);
Ψ(波函数);
ℏ(约化普朗克常量);
λ(波长);
t(时间);
波粒二象性
·黑体辐射
当加热一枚铁块时,随着温度的升高,它会变红、变黄、变白。我们知道,不同的颜色意味着不同频率的光,即电磁波。更多的实验证明,物体在任何可能达到的温度下都会向外辐射出各种频率的电磁波。这些电磁波的能量按照频率分布,能量不同,则频率不同。这样的电磁波叫作热辐射。
物体在辐射电磁波的同时,还会吸收照射到它表面的电磁波。在理想条件下,能够完全吸收照射在它上面的各频率的所有电磁波的物体叫做黑体。
通过对黑体各种照射实验的研究,维恩从经典的热力学角度以及麦克斯韦分布律出发,导出了一个公式——维恩公式:
M_ν=αν^3 e^((-βν)⁄T)
(其中α、β为常量)
这条公式给出的结果在高频范围和实验结果符合得很好,但在低频的范围内有较大偏差。
此后,瑞利与金斯给出了瑞利-金斯公式:
M_ν=(2πν^2)/c^2 kT
这一公式在低频范围内还能符合实验结果,但在高频范围内便会偏差许多,甚至趋向无穷大。
在黑体辐射领域研究中出现的这一经典物理的失效,曾被物理学家称为“紫外灾难”。
1900年年底,普朗克发表了他导出的黑体辐射公式——普朗克公式:
M_ν=2πh/c^2 ν^3/(e^(hν⁄kT)-1)
这一公式在全部范围内都与实验曲线吻合!但这成功的代价,便是“绝望地”提出了能量量子化的假设。以E表示一个频率为ν的谐振子的能量,普朗克假定:
E=nhν ,n=0,1,2,…
其中,h为普朗克常量(h=6.260755×10^(-34) J∙s)。上式给出的每个能量值被称为“能量子”。
当一束光照射在金属表面上时,金属原子中的电子会被激发,从金属表面逸出,这种现象被称为光电效应,从电子表面逸出的电子叫做光电子。实验与计算得出,要使一种金属产生光电效应,照射光的频率必须要大于某一频率ν_0,这一频率叫做光电效应的红限频率(或极限频率),对应的波长叫红限波长(或极限波长)。红限频率的大小只和金属的种类有关。
有趣的是,比起很强的长波光,微弱的短波光似乎更会使光电子逸出,这是与麦克斯韦的电磁理论——大家已经完全认可的光的波动学说,所完全不能够解释的。这是因为,光的波动学说认为,光的强度与光的振动幅度有关、光的能量是连续地分布在光场中的。
在量子理论中,光的能量不连续,是以完整的一个个单元被产生或吸收的。每一份能量就像我们使用的货币一样,不能被任意拆分成无数小份。这一个个能量单元被命名为“光子”。对于光子的能量,爱因斯坦假定,不同频率的光子能量不同,频率为ν的光的一个光子的能量E为
E=hν
爱因斯坦解释,在光电效应中,每一个光子将把自己的能量以完整单元给予一个电子,电子获得能量后,动能便增加了,从而有可能逸出原子。随后,光子的概念就此被证明是正确的。
综合起以往的理论,对于光本性的全面认识就是:光既具有波动性,又具有粒子性。这种本性被称为波粒二象性。光既不是经典意义上单纯的波,也不是经典意义上单纯的粒子。
结合以下公式:
E=mc^2
E=hν
可见,光子的动量为
p=h/λ
这条式子体现,光的粒子性与波动性在数学上是通过普朗克常量联系在一起的。
·是波还是粒子?
1942年,德布罗意在光的波粒二象性的启发下想到:自然界在许多方面都是明显对称的,如果光具有波粒二象性,那么实物粒子,比如电子,也应该具有波粒二象性。于是,他大胆地提出了假设:实物粒子也具有波动性。并且,它将光子的能量-频率和动量-波长的关系式借来,以类比的方式运用在其它粒子上。
和粒子相联系的波被称为德布罗意波(或物质波)。不久后,许多物理学家纷纷用实验验证了他的猜想,陆续证明了电子、中子、质子、原子甚至分子等都具有波动性,德布罗意公式对这些粒子全部正确。更多的实验说明,一切微观粒子都具有波粒二象性,德布罗意公式就是描述微观粒子波粒二象性的基本公式。
·概率?
既然提出了德布罗意波,那它的物理意义又是什么呢?目前得到公认的关于德布罗意波实质的解释是玻恩在1926年提出的。在他之前,爱因斯坦曾提出电磁场是一种场,这种场引导着光子的运动,而各处电磁波振幅的平方决定在各处的单位体积内一个光子存在的概率。玻恩发展了爱因斯坦的思想,保留了粒子的微粒性,而认为物质波描述了粒子在各处被发现的概率。这就是说,德布罗意波是一种概率波。
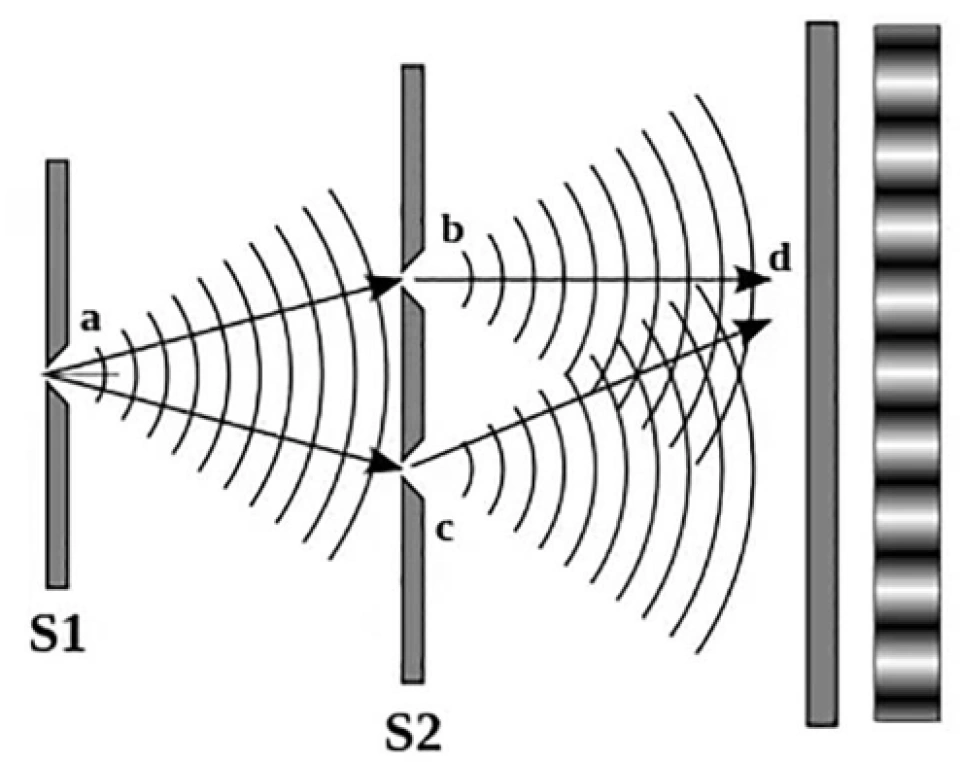
玻恩的概率波概念可以用电子双缝衍射实验来说明,在此之前我们先来了解光的双缝干涉实验:
光的双缝干涉实验
在经典理论中,光是一种波,如上图所示,b点与c点发出的便是两列频率和相位完全相同的光了。
利用惠更斯原理,可以将波阵面(前进波列最前方的波面)上的每一点都看作一个新的波源。
光是波,它的光强函数是周期性的,当两列光相遇时,它们便会发生干涉——就像水面上的水波一样,强和强将变得更强,强和弱相互抵消了部分的波澜。因此,在b、c两缝发出的光经过干涉后,便在后方的屏幕上呈现出了明暗相间的条纹。
下面我们来看电子的双缝衍射实验:
实验装置与光的双缝衍射实验完全相同,只是将入射的光改为电子。如果减弱入射电子束的强度,每一次只有一个电子通过双缝。如果电子是粒子,那么它将有两个选择:走b缝,或c缝。那么结果自然是显而易见的清晰的两条明纹。但随着电子总数的增多,我们发现,屏幕上竟然呈现出了清晰的衍射条纹。如果电子是粒子,那么单独一个电子在穿过b或c缝时又和谁发生了干涉呢?
这个现象可以用概率来解释:电子的运动对应了德布罗意波,它在屏幕上被观测到的位置是由德布罗意波给出的概率大小来决定的,而不取决于电子本身的运动形式。因此,在量子力学中,我们不再能够准确预测粒子“到底”通过了哪个缝,而只能得出它有两种可能的运动方式。
为了定量描述微观粒子的状态,量子力学中引入了波函数,并用Ψ表示。一般来讲,波函数是空间和时间的函数,并且是复函数,即Ψ=Ψ(x,y,z,t)。将波函数与概率波的关系加以推广,玻恩假定,|Ψ|^2=ΨΨ^*是粒子的概率密度(即在时刻t,在点(x,y,z,)附近单位体积内发现粒子的概率)。
我们将波函数用于以上的实验:
以Ψ_1表示单开1缝时粒子在屏幕附近的概率幅分布,那么|Ψ_1 |^2=P_1就是粒子在屏幕上的概率分布,同理有|Ψ_2 |^2=P_2。按照经典的概率理论,粒子在屏幕上的概率分布应该是
P_12=P_1+P_2=|Ψ_1 |^2+|Ψ_2 |^2
但事实并非如此。两缝同时打开时,入射的每个粒子都有两种可能的去向,它们可以“任意”选择其中的一条缝。此时,这不是概率的叠加,而是概率幅的叠加,也就是
Ψ_12=Ψ_1 〖+Ψ〗_2
那么相应的概率分布就应该是
P_12=|Ψ_12 |^2=|Ψ_1 〖+Ψ〗_2 |^2=|Ψ_1 |^2+2Ψ_1 Ψ_2+|Ψ_2 |^2
由此可见,正式这交叉项2Ψ_1 Ψ_2使得粒子体现出了波的特性,即衍射行为。
概率概念的引入在哲学上有重要意义,它使得人们不可能精确地预知结果,而只能预知某些可能结果的概率。有必要指出,粒子的运动遵循概率定律,但概率本身是严格受因果律支配的。
因此,尽管概率的引入是非常成功的,它使得量子力学预言的结果和实验异常精确地相符,是一个很成功的理论,但概率的描述也仅仅是一种数学手段,关于量子力学的哲学基础仍然存在很大的争论。以玻恩、海森伯等量子力学大师为首的哥本哈根学派,坚持波函数的概率或统计诠释,认为它表明了自然界的最终实质。而爱因斯坦与德布罗意则不同意这样的结论,爱因斯坦曾在1927年说过:“上帝不掷骰子。”狄拉克也曾说过:“在我看来,我们还没有量子力学的基本定律。”
参考引源:
《大学物理学》(张三慧等),《新概念物理教程》(赵凯华等),Feynman Lectures on Physics, Learning Notes on Quantum Mechanics(Leng Xuan),Introduction to Quantum Mechanics(David J. Griffiths),Wikipedia,bilibili等。
图片来源:
百度图片,Google Images, 《大学物理学》(张三慧等)。
【本文为耀星会的原创作品,未经允许,禁止盗用、转载、篡改文章,否则耀星会和作者将追究版权责任。】




![[s-2]](https://www.bokeyuan.net/pic/image/emoji/cas/2.png)











