科普驿站 第四十九期
主题:时光机与任意门(第三期)
难度:B1-B2
讲师:弦轴子
上节我们讨论了最简单的虫洞一一史瓦西虫洞,它是根据史瓦西度规改造而来的。我们也用新的物理图像工具一一彭罗斯图说明了这种虫洞是不可穿越的,准确来说就是只允许类空世界线走的。因此,史瓦西虫洞没办法被改造成时间机器除非我们超光速。
聪明的你一定会想到,既然我们改造了史瓦西度规,那么广义相对论中的其他度规呢?比如我们能否像改造史瓦西度规一样改造其他度规呢?其实可以的,不过要更复杂一点。
比如克尔黑洞其内部的克尔虫洞就是由克尔度规改造而来的,它就是类时的,不同于史瓦西黑洞中的类空。
因此,克尔虫洞存在闭合类时曲线,可以被改造成时间机器。
下面我们就来简单说说这个情况。
对于克尔黑洞,其实就是广义相对论的克尔解。它是考虑旋转,轴对称性的情况下的。
克尔黑洞的时空线元是:
可以看出比史瓦西时空的线元复杂很多倍。
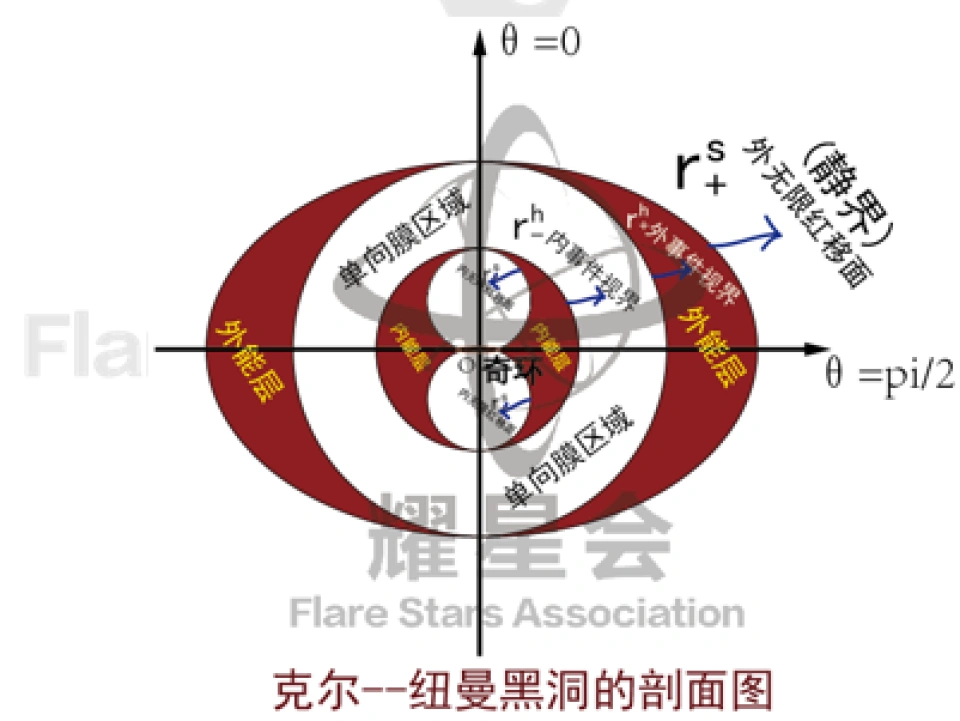
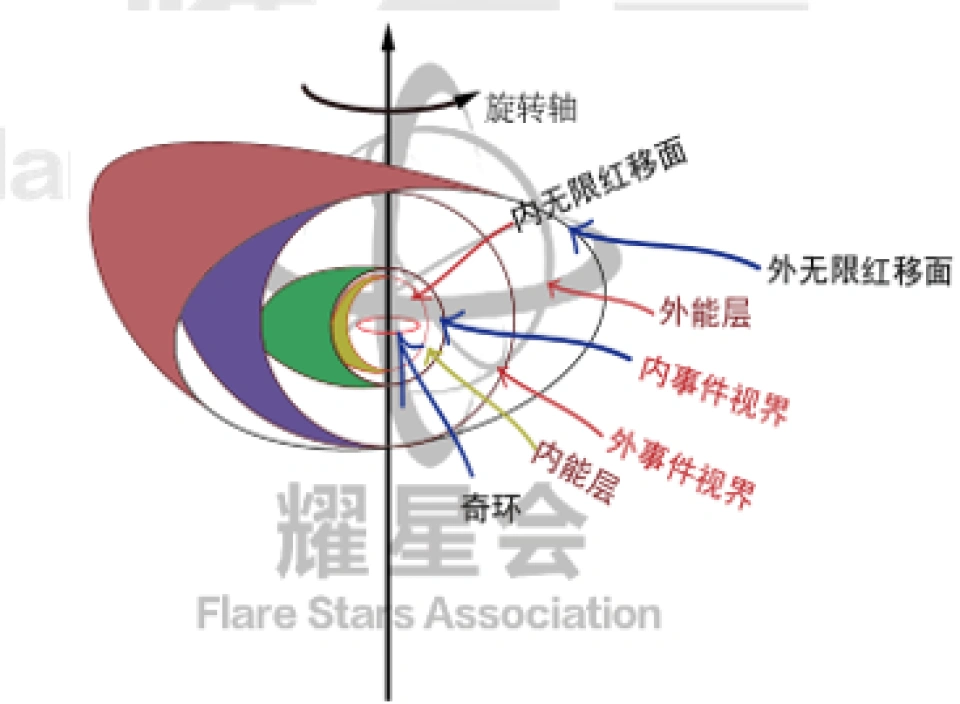
我们也可以得到克尔黑洞的时空结构图:
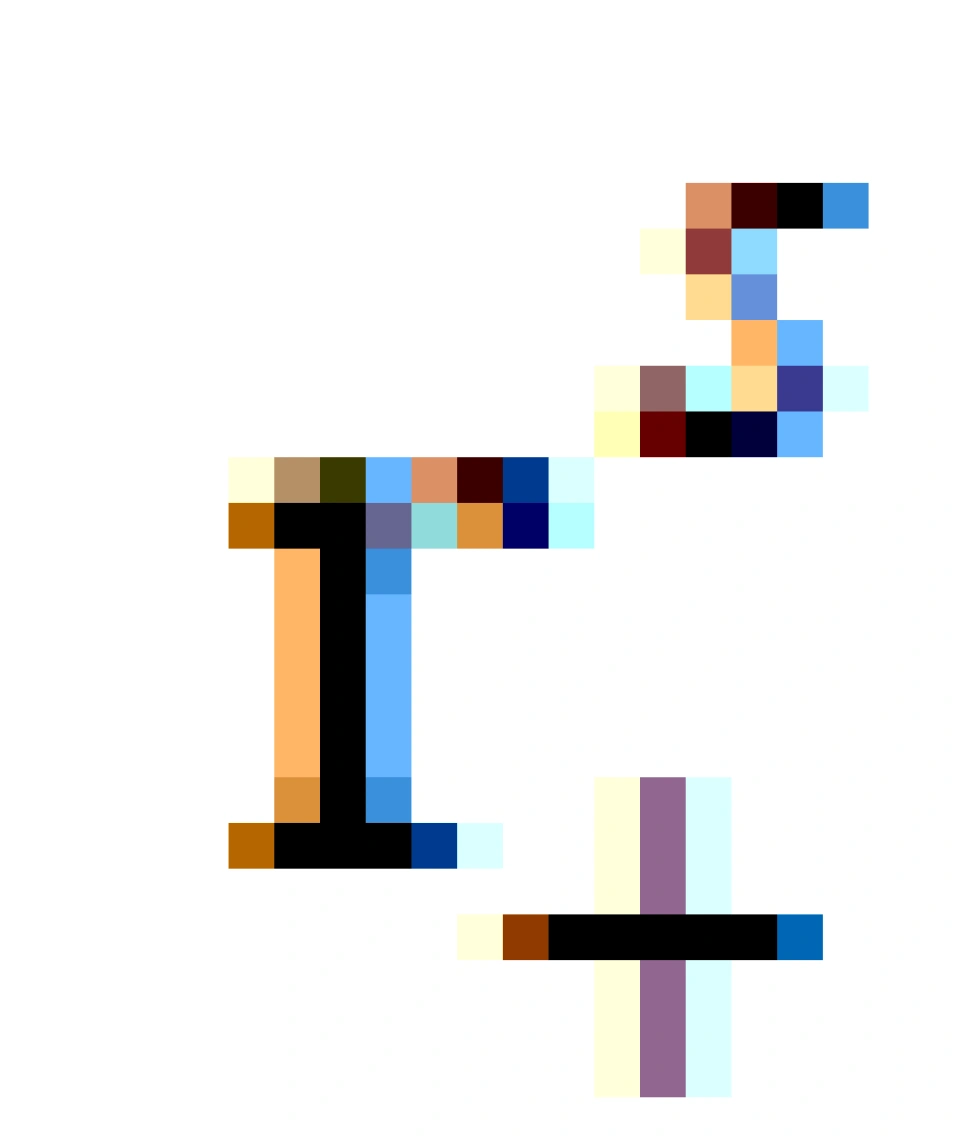 是外无限红移面,在这个面的外面
是外无限红移面,在这个面的外面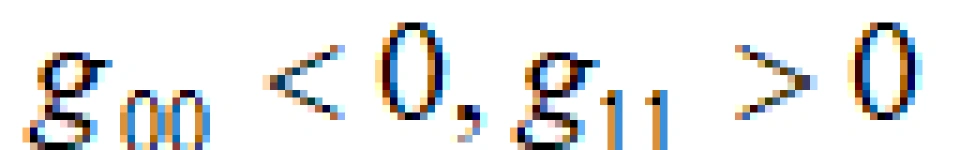 ,跟我们外部宇宙一样。
,跟我们外部宇宙一样。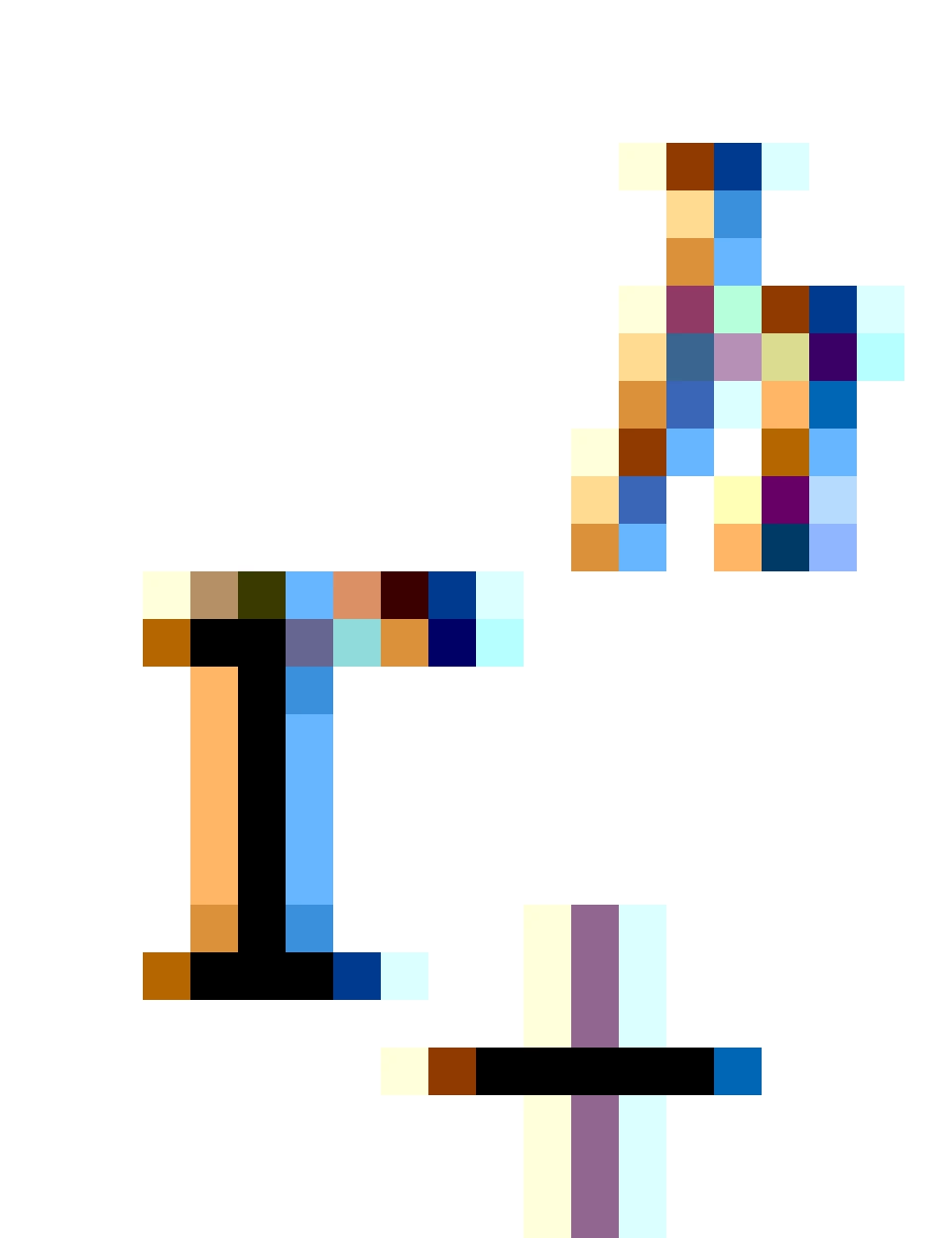 是外视界,中间包裹的阴影区域是外能层,这个时空概念看不清楚。
是外视界,中间包裹的阴影区域是外能层,这个时空概念看不清楚。
因为在这里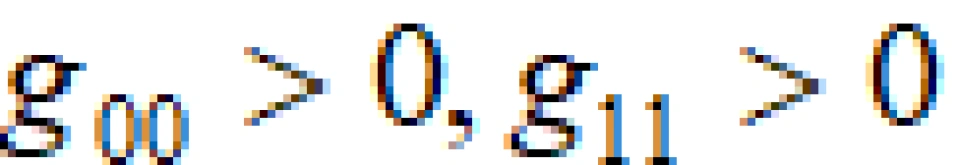 ,所以根本就看不清楚哪个坐标代表的是时间,哪一个代表的是空间。上面我们说过,时空度规的一正三负正好对应着一个时间和三个空间,但是这里的时空度规对角元素都是正的。所以,这里的时空概念其实很混乱,我们根本弄不清楚。
,所以根本就看不清楚哪个坐标代表的是时间,哪一个代表的是空间。上面我们说过,时空度规的一正三负正好对应着一个时间和三个空间,但是这里的时空度规对角元素都是正的。所以,这里的时空概念其实很混乱,我们根本弄不清楚。
时间和空间坐标不再是外部世界表述的那样,它只允许类空世界线通过,因此任何物体都不可能在这里停留下去,并且在这个区域的物体会受到黑洞自转拖拽时空的影响,也就是所谓的时空漩涡,旋转方向就是黑洞自转的方向。这个被称为时空拖拽现象。
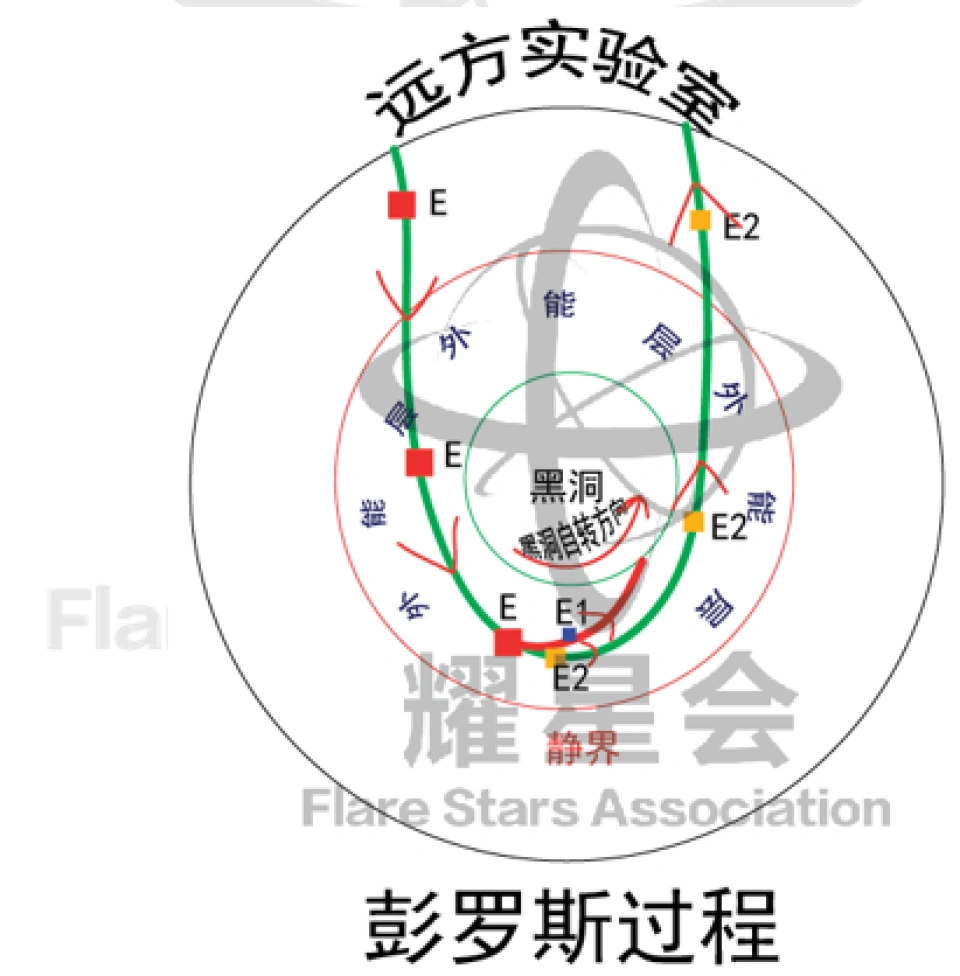
能层还有一个很好的物理现象,丢入一个物体,它会盗取黑洞的旋转能,从而以比入射动能还要大的动能射出来,当然这个物体的一部分要掉入黑洞。这个过程被称为彭罗斯过程。
如果以后在宇宙中发现这种克尔黑洞,人们就可以利用它来获取能源。这样会使黑洞自转速度越来越慢。
之所以会这样,是因为能层中存在着角动量为负的轨道。
我们都知道,在相对论的框架下,能量和动量其实是一家人。它们分别是四维动量在时间和空间上的分量或者说投影。
说到这里,我们来简单温习一下相对论的四维矢量语言框架。
我们之前说过,惯性参考系的变换下,有一个不属于坐标系变换的物理量一一时空间隔或者叫时空线元。记作:ds。并且根据这个定义了固有时间概念。
固有时间:
固有时间才是物体实际经历的时间,它跟坐标时间dt相差一个相对论因子γ。
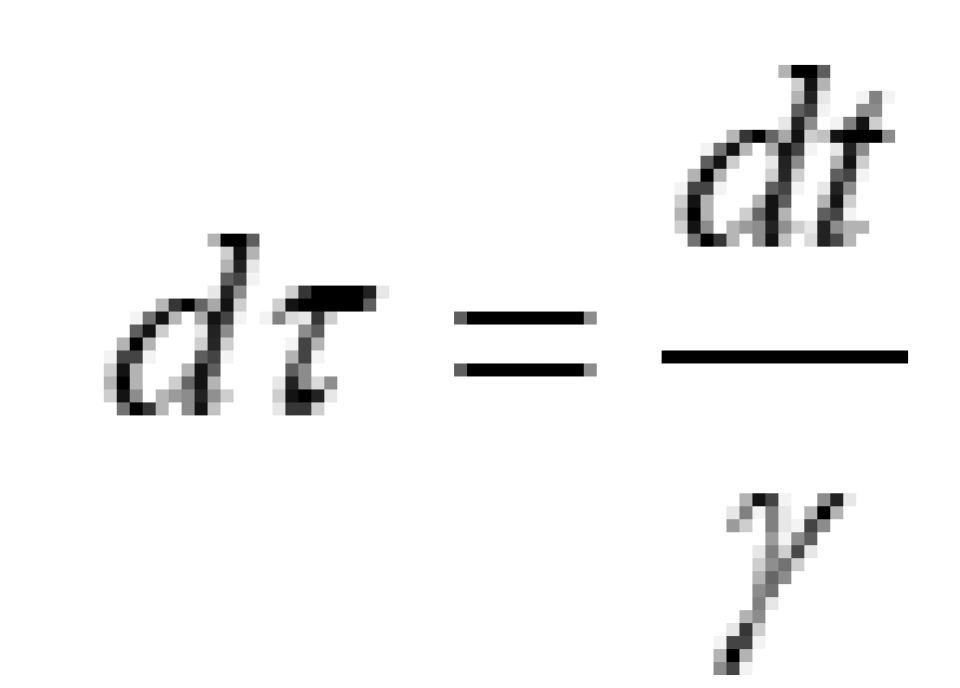 有了固有时间就可以定义四维速度。很好定义,就是四维矢量
有了固有时间就可以定义四维速度。很好定义,就是四维矢量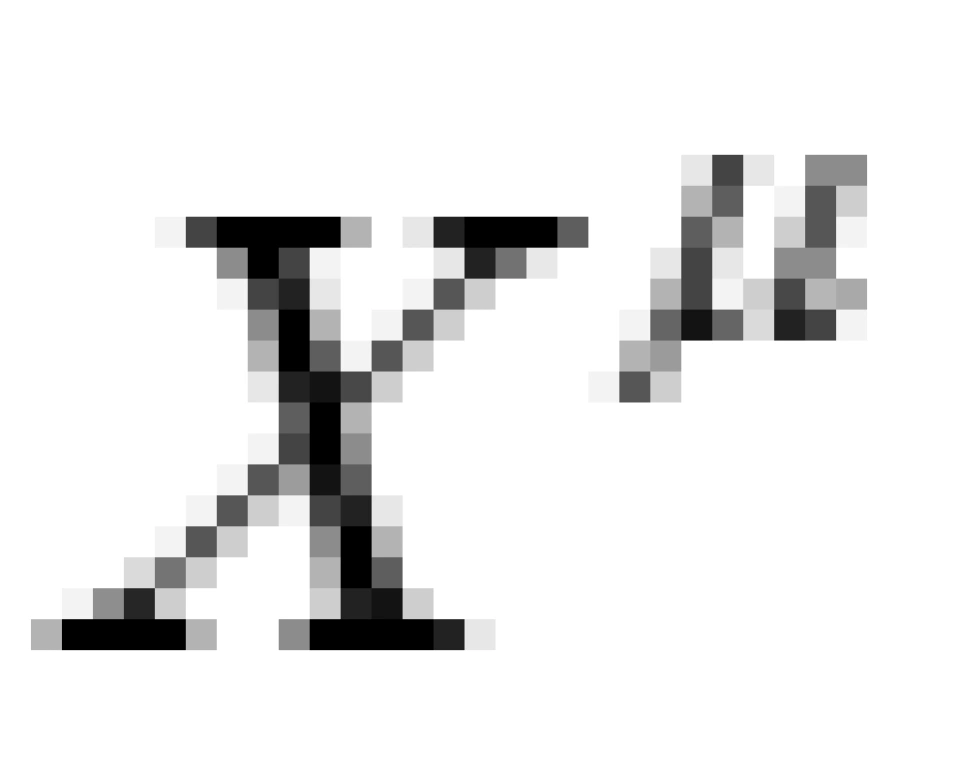 对于固有时间
对于固有时间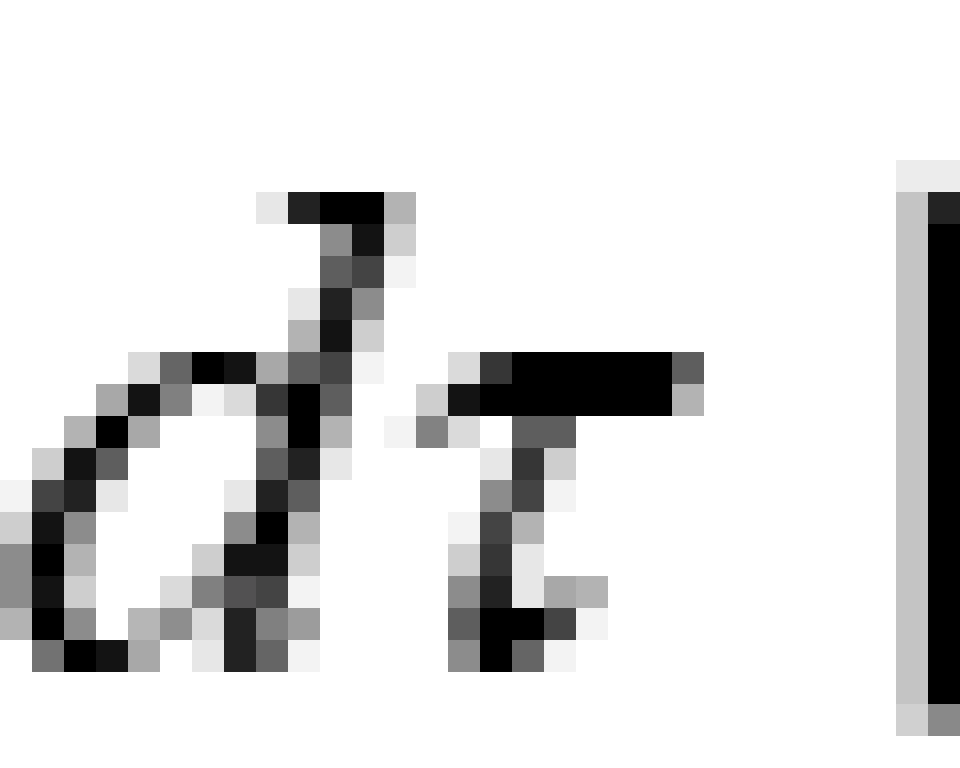 的求导:
的求导:
其中:
这里的1其实就是光速c。
有了四维速度,我们就可以定义四维动量。其实就是质量乘以四维速度: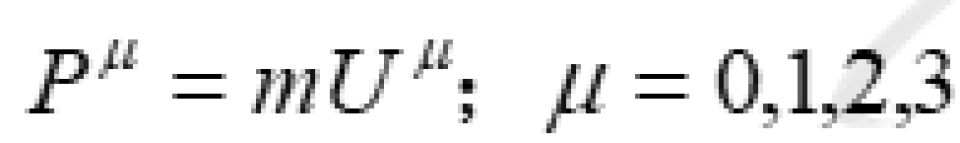 。
。
更进一步的,
到这里我们可以清楚看到时间上的分量或者投影,其实就是能量,空间部分就是动量。
(其实,由于我们采用自然单位制,而在国际单位制下是这样的: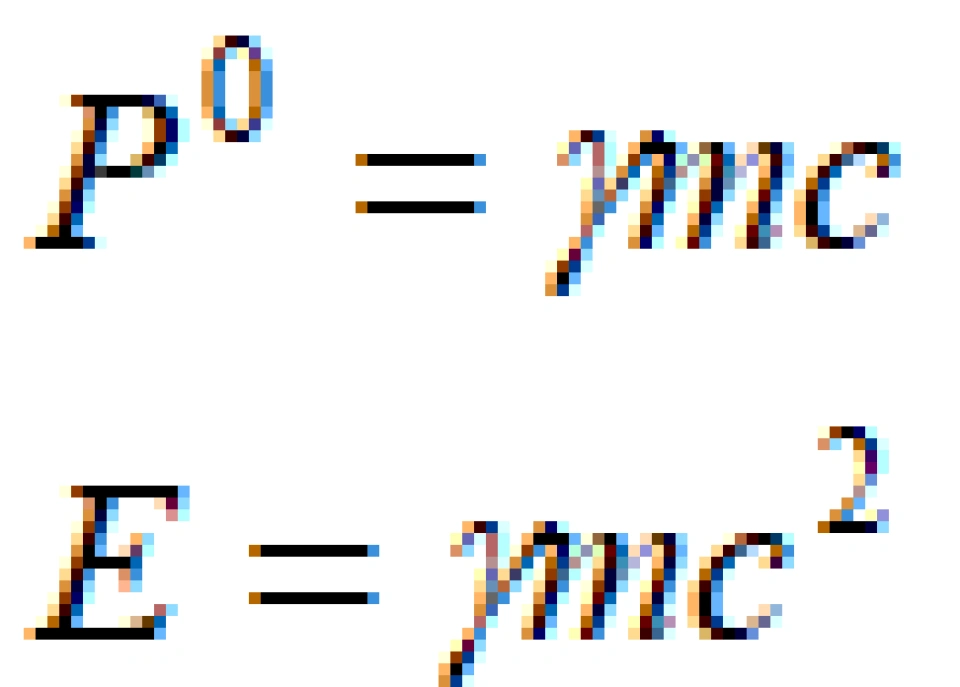 ,不难看出四维动量的第一个分量与能量其实是差一个光速c。不过,这都无伤大雅,不影响最终的结论。)
,不难看出四维动量的第一个分量与能量其实是差一个光速c。不过,这都无伤大雅,不影响最终的结论。)
在相对论的框架下,能量和动量可以组合成一个统一的四维动量去描述。
四维动量在时间轴上的投影定义为能量,在空间轴上的投影定义为三维动量。四维动量本身也是绝对的,但是它在空间轴或者时间轴上的投影则是相对的,依赖于坐标系的选择。
四维动量这些四维矢量的物理量不随坐标系的选择而变化,但是它们的分量会随坐标系的选择而变化。
能量就是四维动量在时间坐标轴/时间坐标曲线上的投影。
在弯曲时空中,时间坐标曲线一定是类时的,因为只有这样我们才可以走。也就是这个时间坐标曲线上每一点的切矢量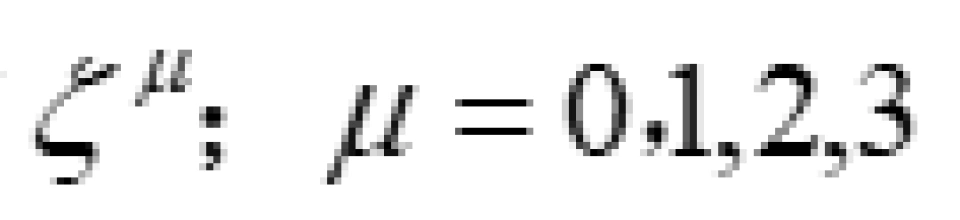 一定满足:
一定满足:
不过呢,在能层里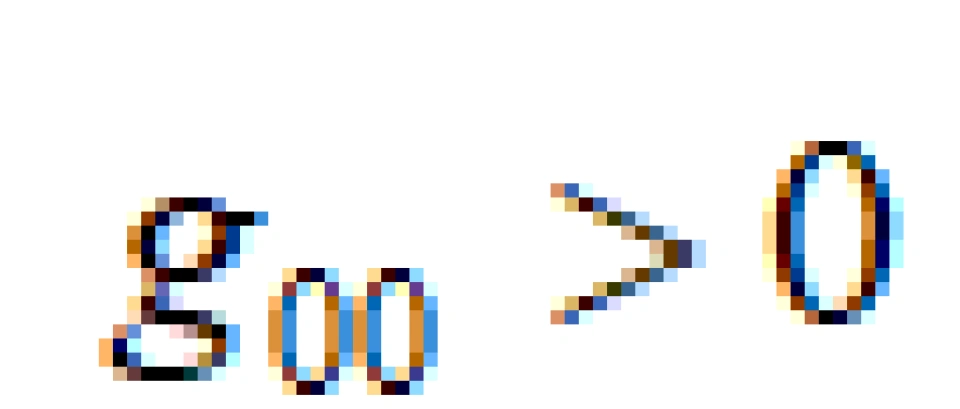 。这也就是告诉我们时间坐标曲线在这个能层里是类空曲线。能量的定义是四维动量在这个时间坐标曲线上的投影,如果时间坐标曲线是类时的,也就是在外部的正常时空,那么能量一定是正的;如果是类空的,那么能量可能是正的,也可能是负的。所以在能层里除去通常的正能量轨道之外,还存在负能量轨道。这些负能量轨道都是角动量为负的轨道,也就是跟黑洞的自转方向相反的轨道。
。这也就是告诉我们时间坐标曲线在这个能层里是类空曲线。能量的定义是四维动量在这个时间坐标曲线上的投影,如果时间坐标曲线是类时的,也就是在外部的正常时空,那么能量一定是正的;如果是类空的,那么能量可能是正的,也可能是负的。所以在能层里除去通常的正能量轨道之外,还存在负能量轨道。这些负能量轨道都是角动量为负的轨道,也就是跟黑洞的自转方向相反的轨道。
因此,如果一个无穷远处能量为E的物体在不受任何外力的作用下飞向黑洞,将沿着测地线(弯曲时空中的直线)运动。那么当它进入能层之后分裂成两块,其中一块所具有的能量为 的碎片沿着负能量轨道进入黑洞内部,而另一块所具有的能量为 的碎片能够逃出来。
由于能量守恒,则有:
但是,由于进入黑洞的那块碎片,它是沿着负能绕轨道进入的,所以它具有的能量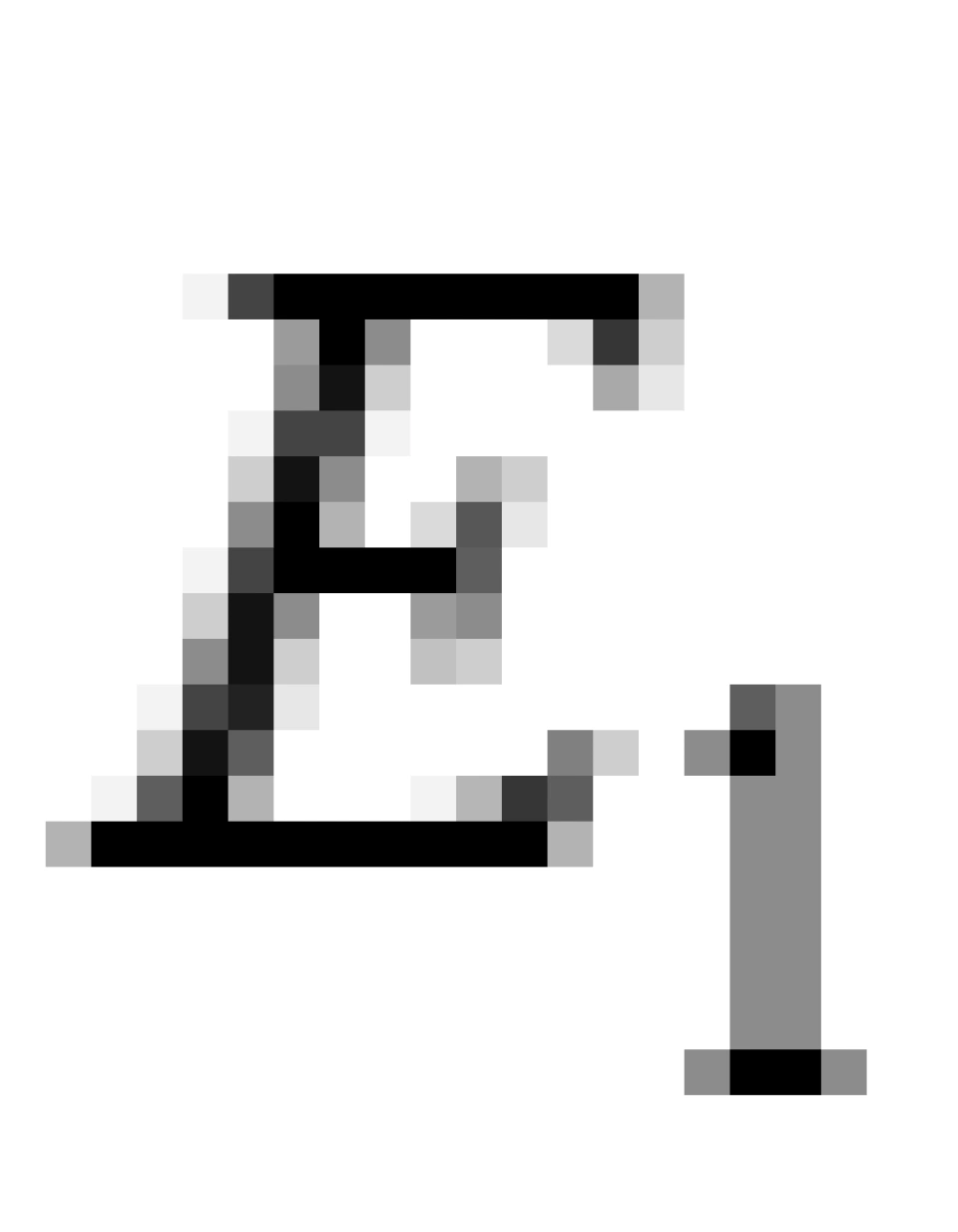 是小于0的。这将导致
是小于0的。这将导致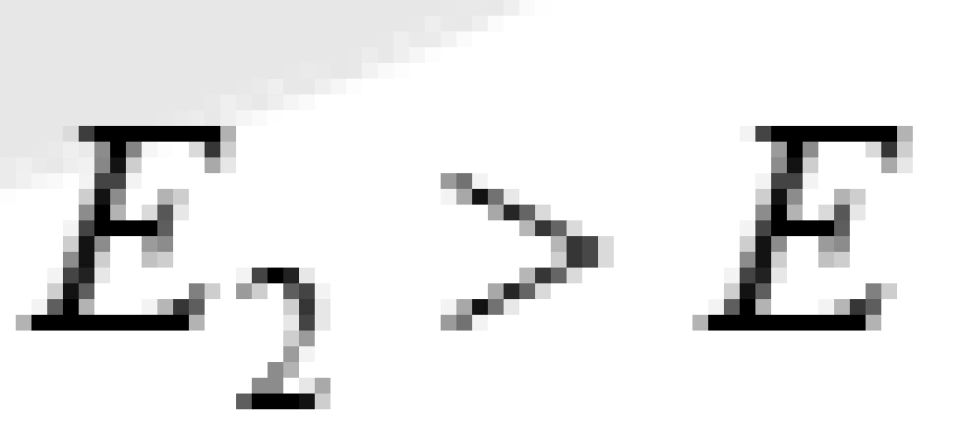 ,这意味着,在无穷远处实验室的观察者得出的结论是:物体的出射能量大于入射能量,也就是说他能用这种方法从黑洞的能层中提取能量。这一效应就被称之为彭罗斯过程。
,这意味着,在无穷远处实验室的观察者得出的结论是:物体的出射能量大于入射能量,也就是说他能用这种方法从黑洞的能层中提取能量。这一效应就被称之为彭罗斯过程。
另外,由于进入黑洞内部的物体是沿着负能量轨道进入的,所以说这个物体具有的角动量是负的。而这个负的角动量将由黑洞的角动量去偿还,所以黑洞会越转越慢。
不过值得注意的是,如果有一个观察者也在能层之内,那么无论观察哪一个碎片,它所具有的能量都是正的。但是对于无穷远处实验室的观察者来看,沿着负能量轨道进入黑洞内部的碎片所具有就是负的。能量不是一个坐标不变量,但是它是一个守恒,所以黑洞偿还了这些东西。
彭罗斯过程的微观版本就是米纳斯超辐射,进入黑洞的物体是具有量子效应的。也可能是一束光或者是任何粒子。如果是带电粒子,那么黑洞将会损失电磁能量。
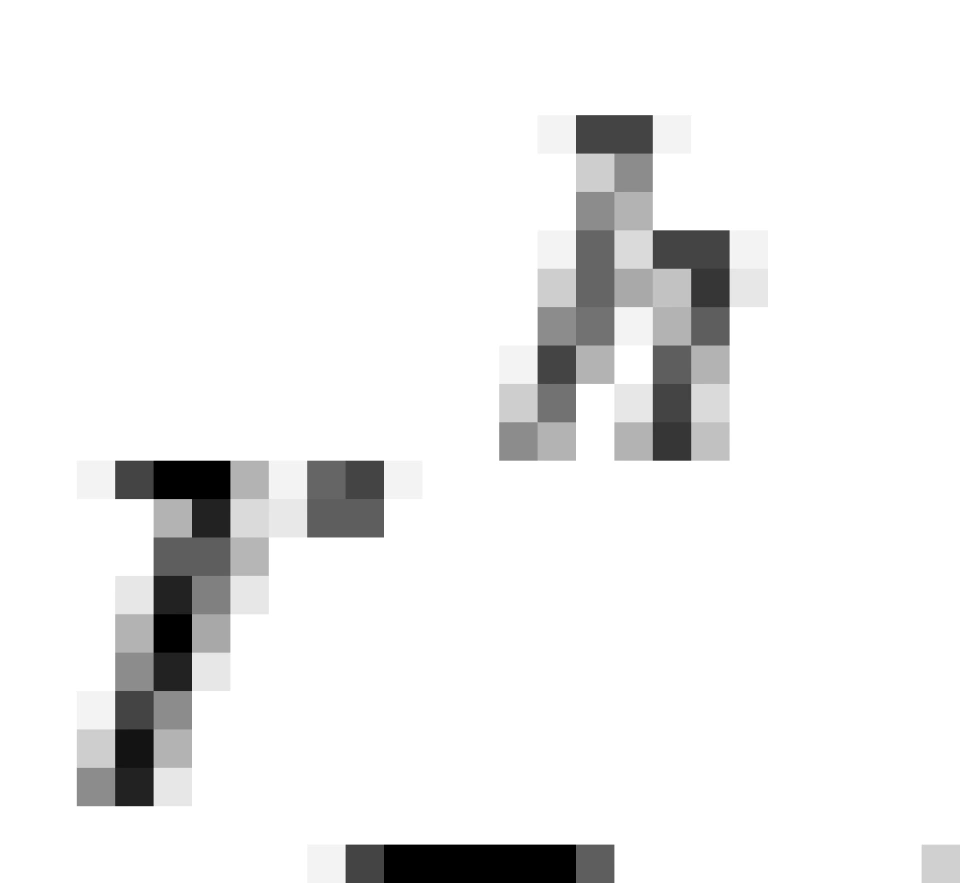 是内视界,
是内视界,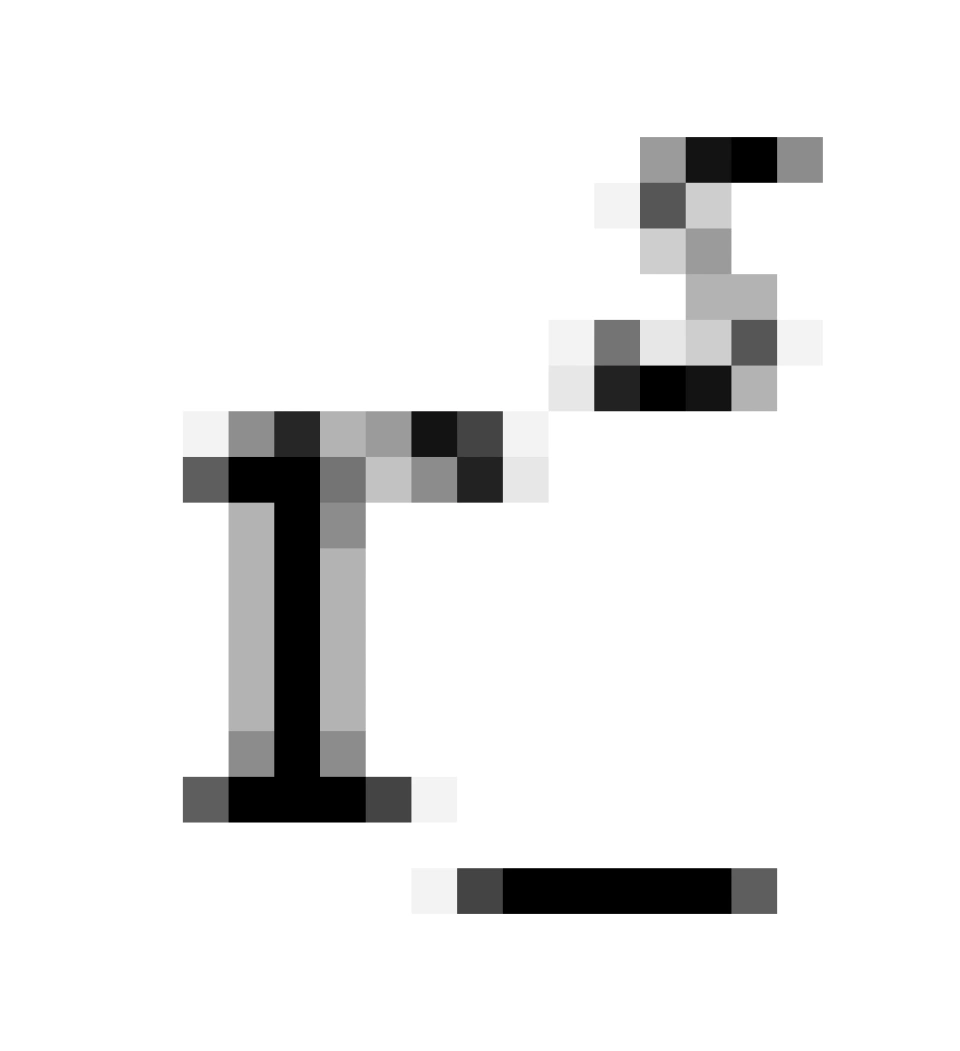 是内无限红移面,这两个之间包裹的区域叫做内能层,这里的时空概念同样也看不清楚。
是内无限红移面,这两个之间包裹的区域叫做内能层,这里的时空概念同样也看不清楚。
内外视界包裹的区域是单向膜区,因为在这里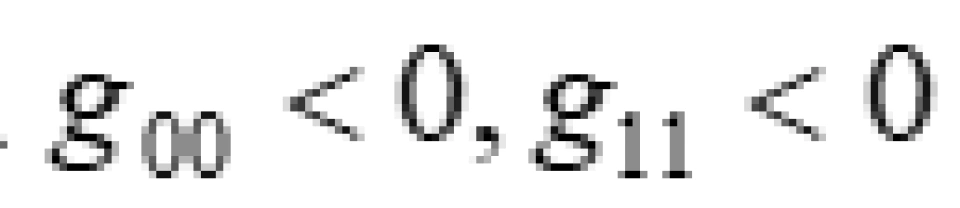 ,时间坐标充当空间的角色而空间坐标充当时间的角色。所以说会不可避免地撞到内视界中,就如同我们上面介绍史瓦西黑洞内部情况一样。在那里,物体不可避免的撞向奇点。在这里,物体进入了就不可能回到克尔黑洞外面。
,时间坐标充当空间的角色而空间坐标充当时间的角色。所以说会不可避免地撞到内视界中,就如同我们上面介绍史瓦西黑洞内部情况一样。在那里,物体不可避免的撞向奇点。在这里,物体进入了就不可能回到克尔黑洞外面。
而图中的“8”字形里面也就是内无限红移面之内的区域,这里的时间和空间概念跟黑洞外面的时间和空间概念一样。这意味着这个区域有可能跟我们外部的宇宙一样。
与史瓦西黑洞不同的,克尔黑洞的奇点其实是一个环。
由于奇环是在内无限红移面所包裹的区域之内,而那里又和外部的宇宙一样是正常的时空概念,并且也不是单向膜区,因此,那里的物体可以很自由自在地在这里运动。
在这里时间坐标t充当时间的角色,而是空间坐标r则继续充当空间的角色。
克尔黑洞奇环/奇异性,也就是r=0就变成一个等空间面。这个面跟时间方向平行。这种奇异性被称为类时奇异性,所以克尔黑洞奇环被称为类时奇点。但是奇环具有强大的斥力,物体不会撞到奇环,但是有可能从中间穿过去。不过,大部分人认为这个区域往往是不稳定的。
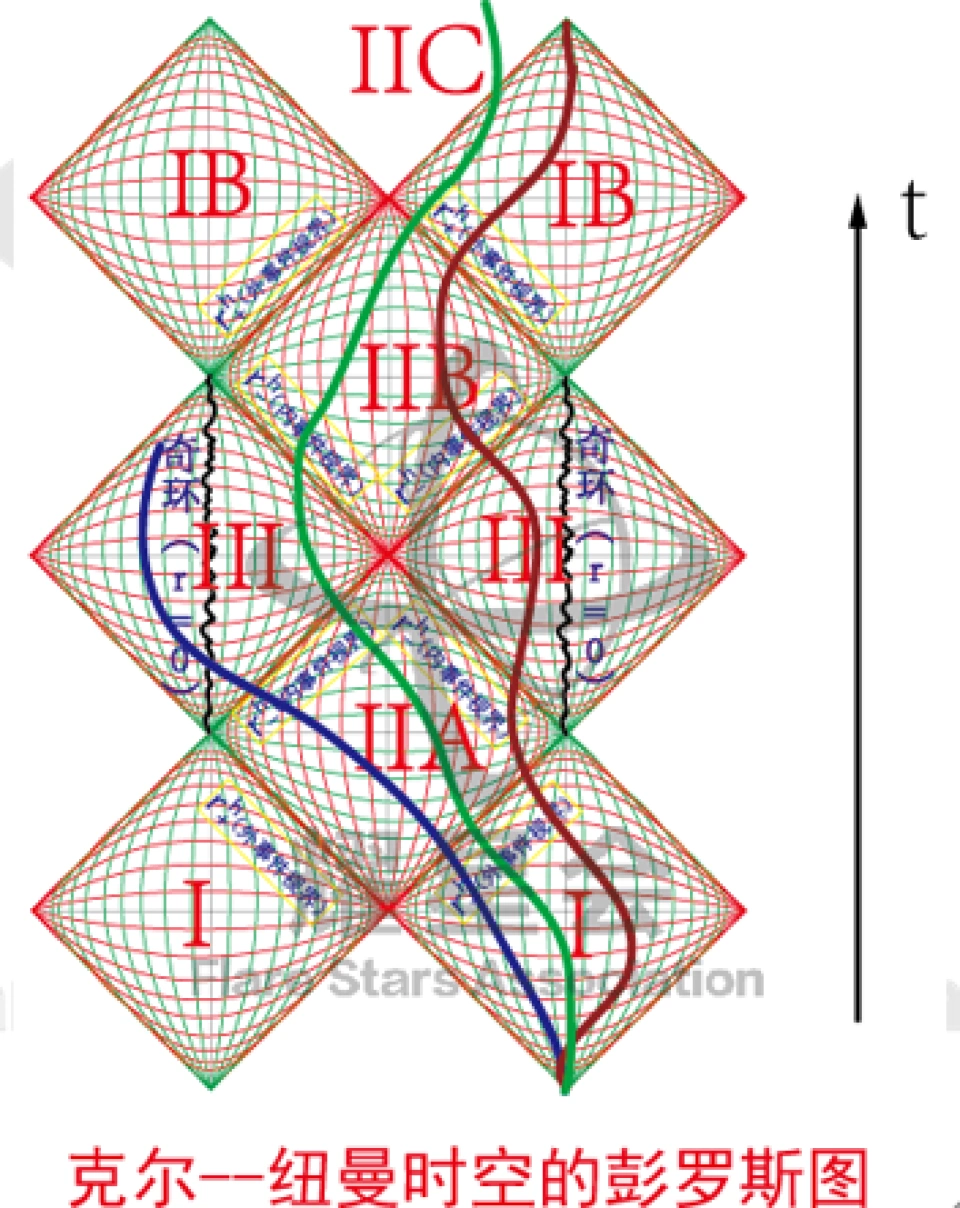
现在我们来看一下克尔黑洞的彭罗斯图就一切都明白了。
r=0就是奇环处,图中几个穿插的线就是世界线。
I区是外部的宇宙,也就是我们所生活的宇宙。II是单向膜区,而III则是内视界包裹的时空区域。这里的时空奇点或者叫奇环跟史瓦西的不同,它是类时的,因此是允许物体通过它的。
蓝色世界线将穿过奇环,进入一个反引力宇宙,至于这里到底是什么地方,目前也不知道。
红色世界线和绿色世界线将穿过奇环,进入一个正常的宇宙。克尔黑洞的彭罗斯图理论上是上下无限延伸的。仔细看图,沿着时间方向走,看好等时间线和等空间线,就可以看懂每个区域代表什么。
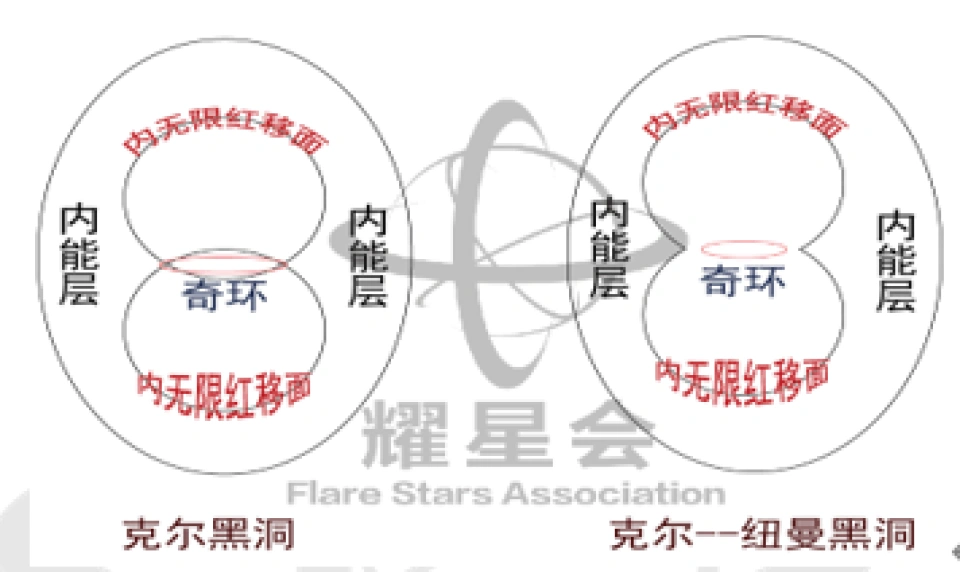
对于第3种普遍的情况,克尔——纽曼度规,跟这个差不多。但是最大的区别在于奇环与内能层的关系。
图中左边是克尔黑洞,右边是克尔——纽曼黑洞。两个黑洞的黑洞结构只有这方面不同,其它的都差不多。
不过这两种改造而来的虫洞即使允许类时曲线通过,也是不稳定的。它会在某种量子真空微扰作用,跟内视界重合,从而从只允许通过类时世界线变成只允许通过类光世界线。
更不要说穿过它需要面临巨大的引力,这充满了很多危险。你要穿过黑洞的事件视界,到达奇点或者奇环附近。这已经是九死一生了。因此,这两种绝不可能被用作时间机器的候选人。
可充当时间机器可被我们穿过的虫洞,最好没有事件视界,没有强大的引力,否则就会撕裂我们。而且该时间机器最好可以在某种微扰下保持稳定。当然虫洞的时空结构与附近的物质分布必须满足广义相对论。这将意味着,我们无法用黑洞来类比构造出这种我们所需要的虫洞。我们将无法得知它的起源。不过这个问题最终在上世纪80年代被索恩他们成功解决,他们是通过时空结构类比反推的。关于具体他们怎么解决的,下期将会讲到。
参考引源:
《广义相对论基本》,赵峥,刘文彪
《广义相对论》,刘辽,赵峥
《黑洞的热性质与时空奇异性–零曲面附近的量子效应》,赵峥
《黑洞与弯曲的时空》,赵峥
《微分几何入门与广义相对论》上中下册,梁灿彬
【本文为耀星会的原创作品,未经允许,禁止盗用、转载、篡改文章,否则耀星会和作者将追究版权责任。】


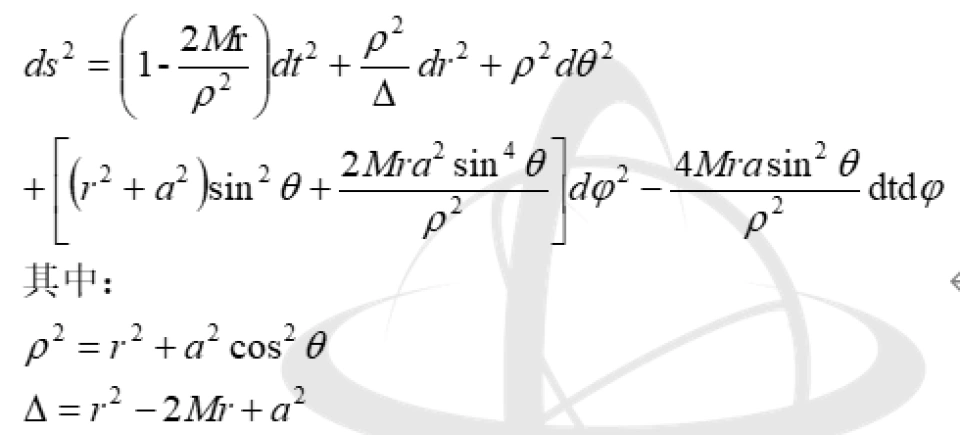
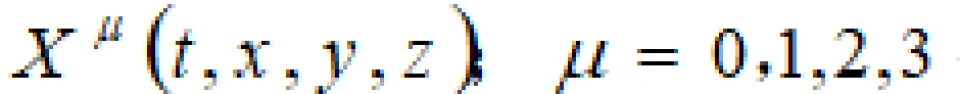
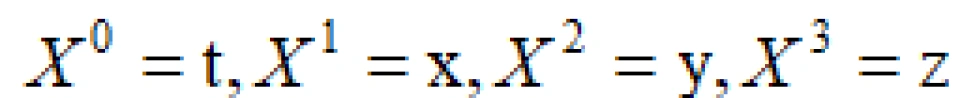
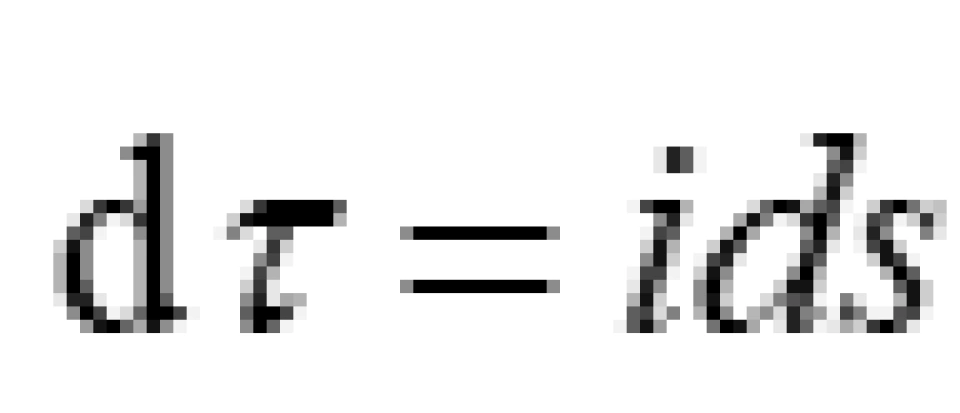
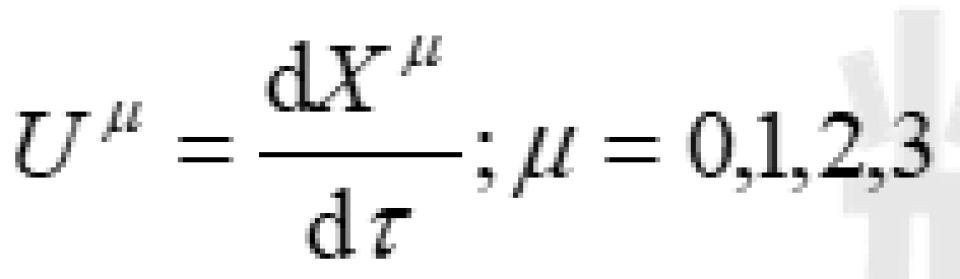
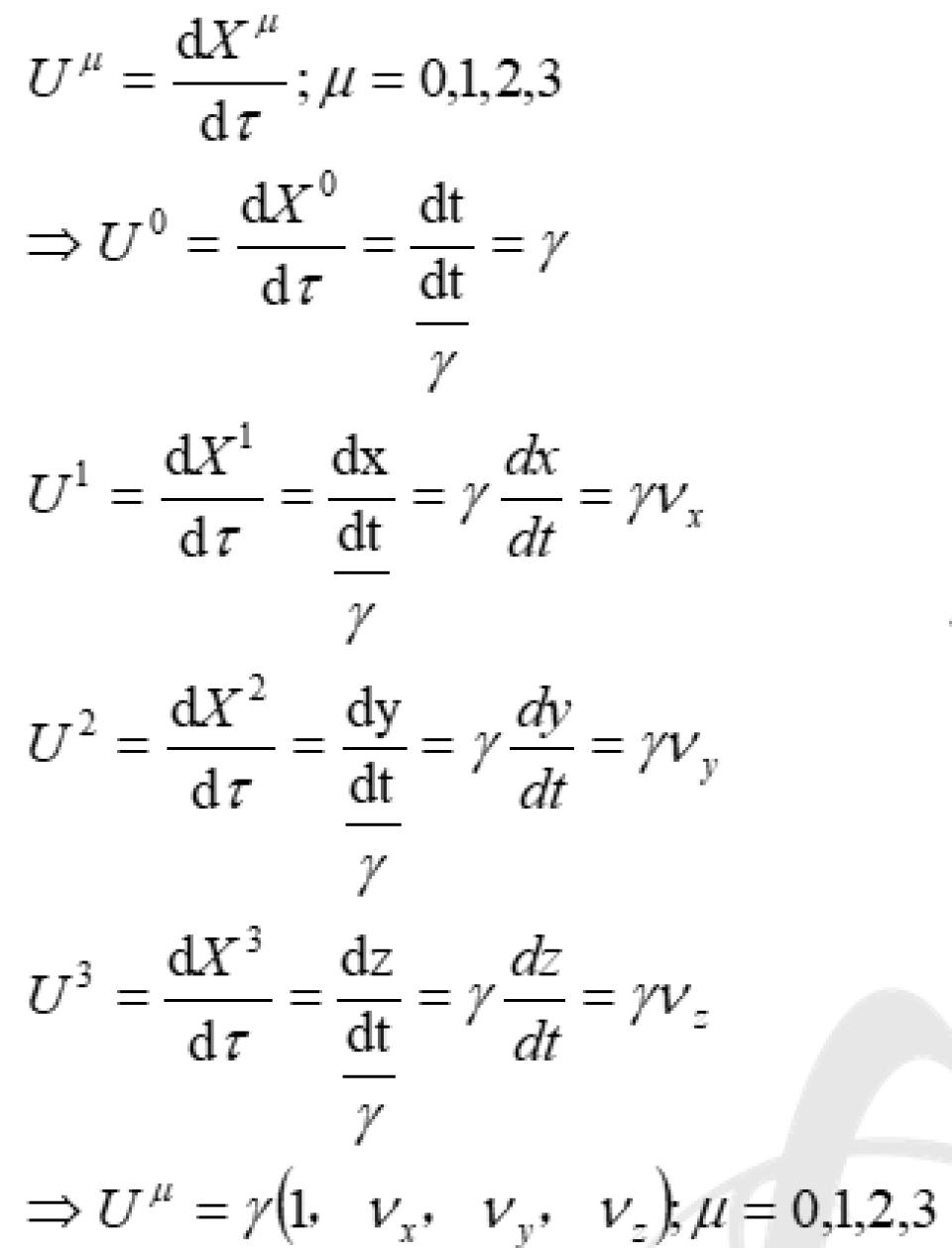

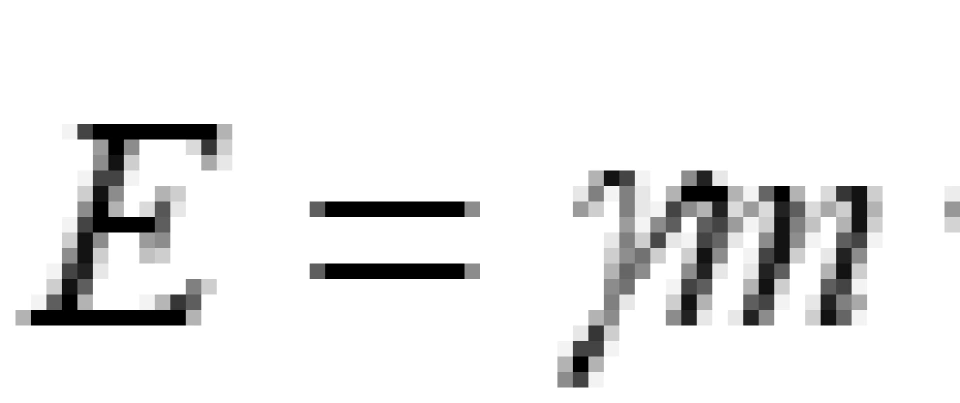
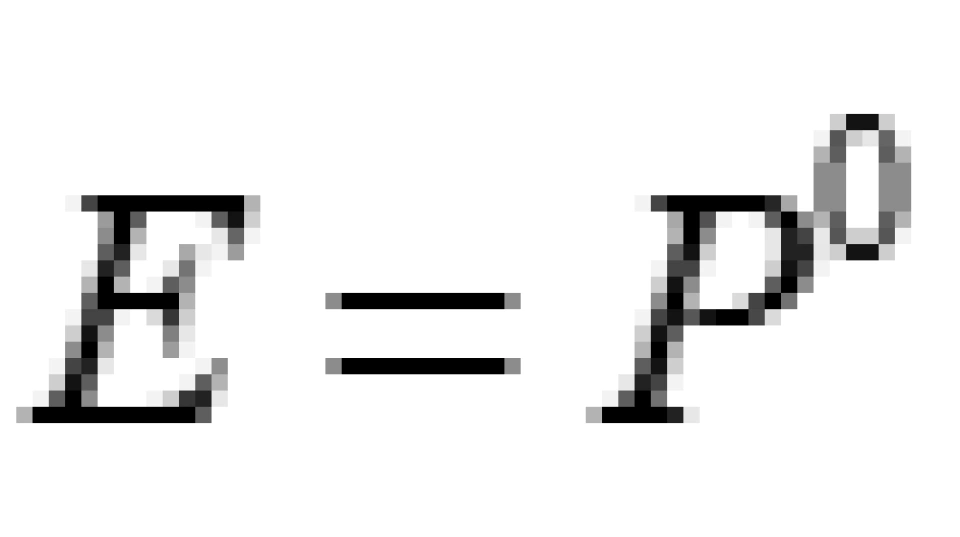
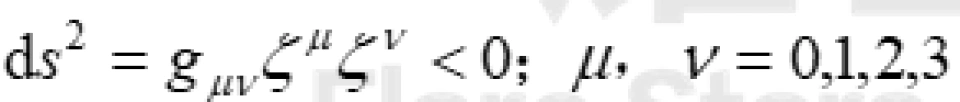
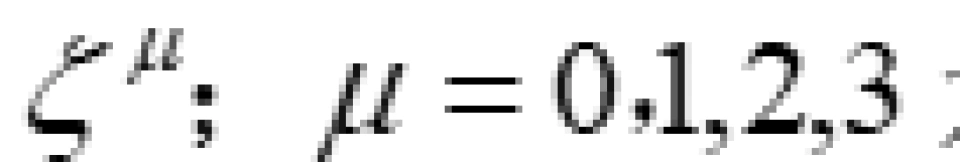
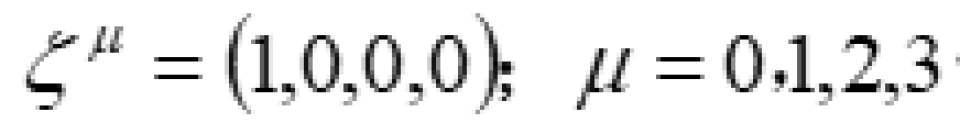
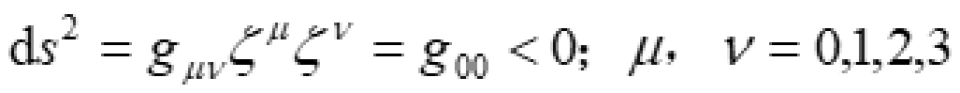
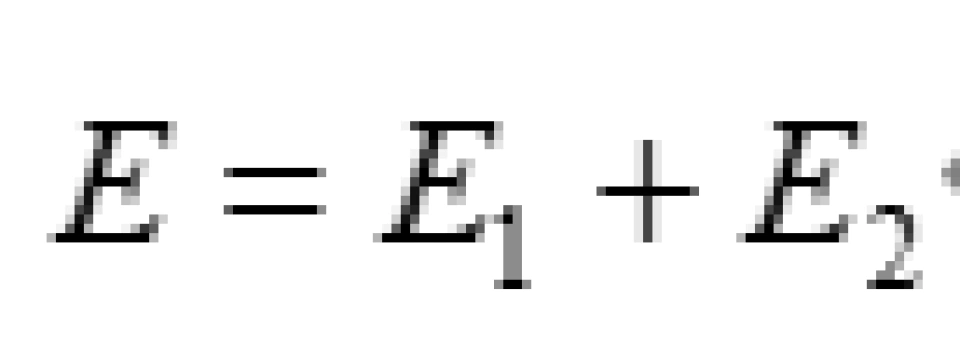

![[s-58]](https://www.bokeyuan.net/pic/image/emoji/cas/58.png)
![[s-59]](https://www.bokeyuan.net/pic/image/emoji/cas/59.png)











