科普驿站 第四十三至四十四期
科目:数学
难度:B2
讲师:GHOSTS
下 2020..1.31
椭圆运动
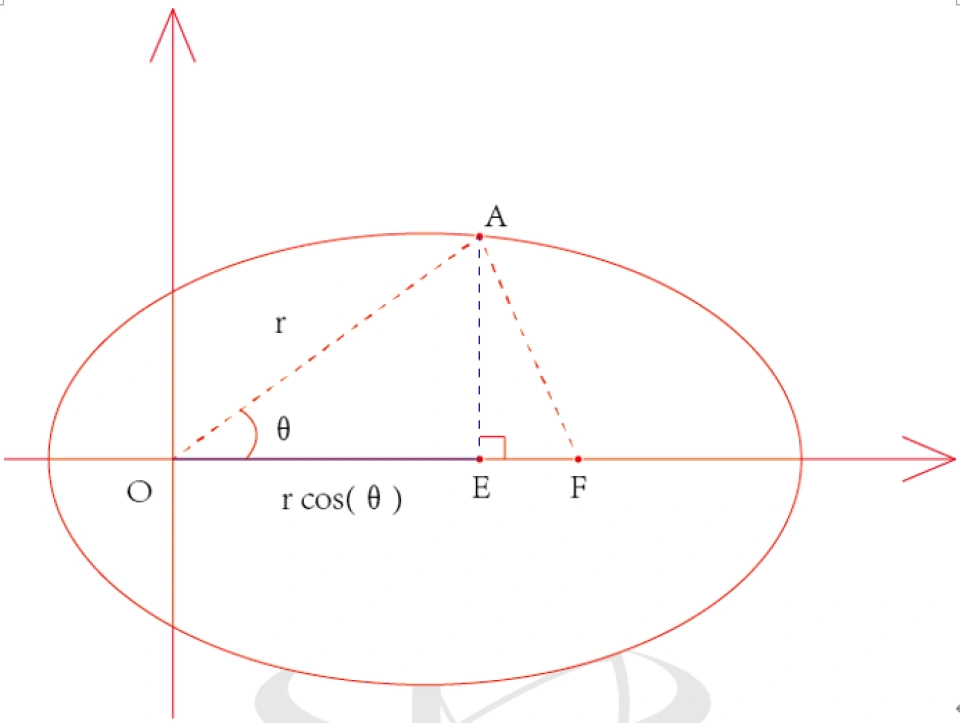
与传统的极坐标相区别,在处理天体物理的时候,中心是焦点,在焦点处做坐标系。举个例子吧,比如说太阳和地球之间那个轨道,就是太阳的位置就是在焦点处。
其中的c部分,是由于椭圆的性质,因为OA加OF为定值,为2a(a指的是半长轴)。两个焦点的距离为2c,A与b(半短轴)和c满足a²=b²-c²。
e部分指的是在三角形AOE中:
e为离心率,p为焦点到准线的距离。
这是椭圆的极坐标,最后化简得出的结果。如果求出来的轨道满足该方程的话,则该轨道为椭圆。
万有引力公式
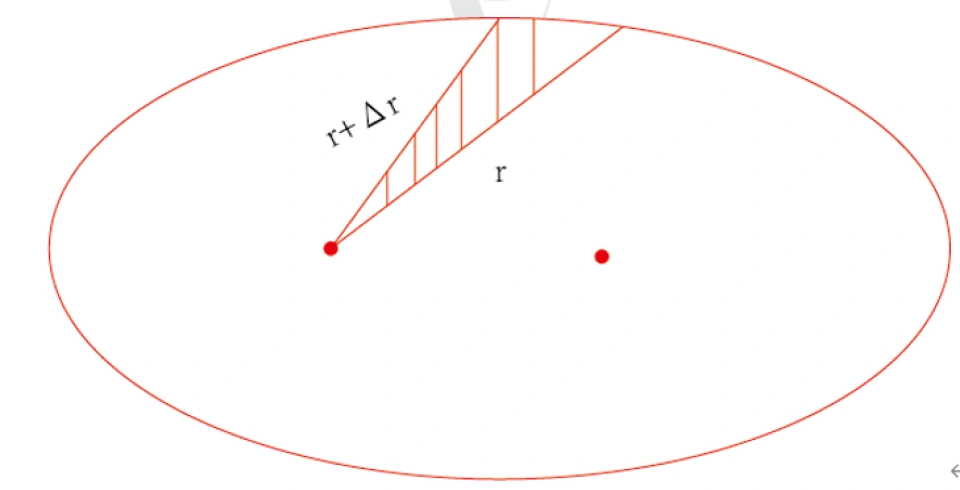
以这两个式子为前提,来进行下一步计算。首先根据开普勒第二定律可得:
此处的a部分可以参考以下b部分的计算:
首先凑一个常数m,因为c,m为常数,则r^2 dθ/dt也为常数,因此就有了c步骤。接下来结合开普勒第三定律:
T为周期,a为半长轴。将a部分的计算代入以下公式:
可以求出b部分。
由
其中:
到了这步,和最终公式已经很接近了。
在力学中,引力为负号,斥力为正号,便可得出万有引力公式。
【本文为耀星会的原创作品,未经允许,禁止盗用、转载、篡改文章,否则耀星会和作者将追究版权责任。】
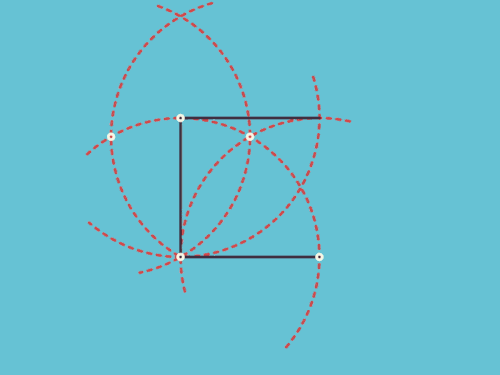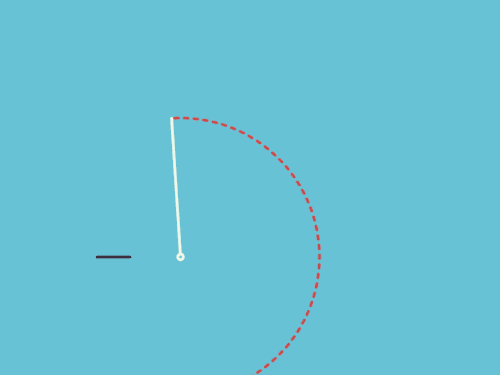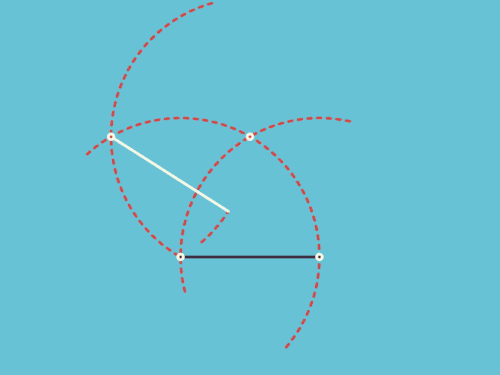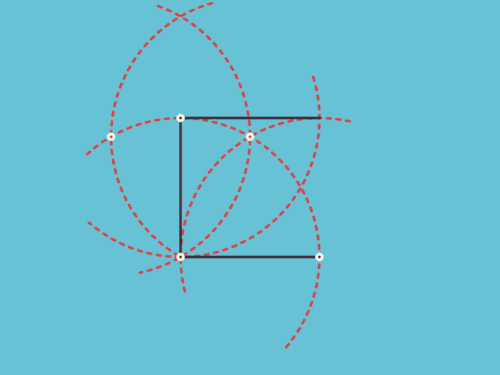

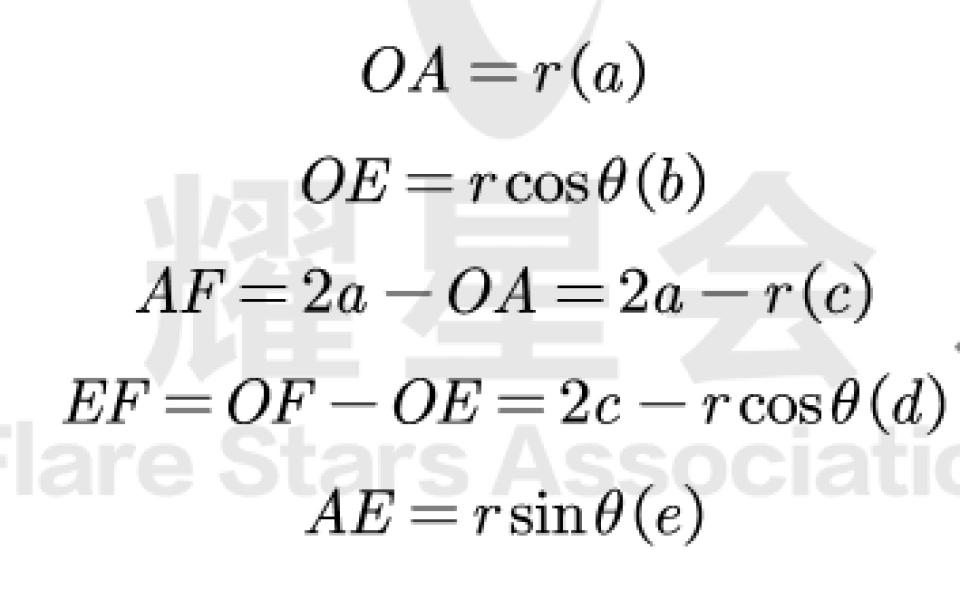
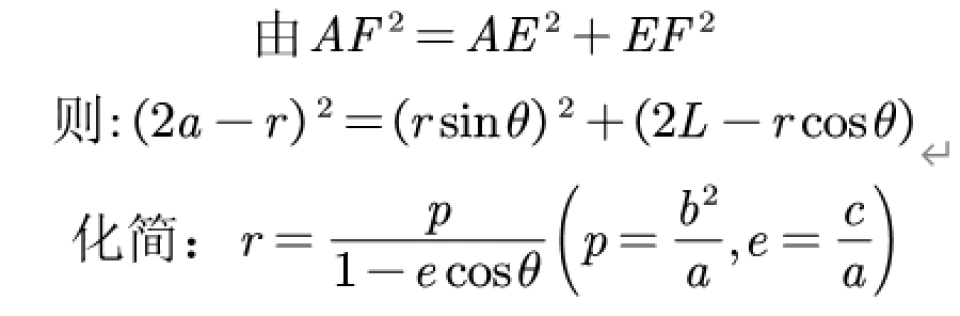




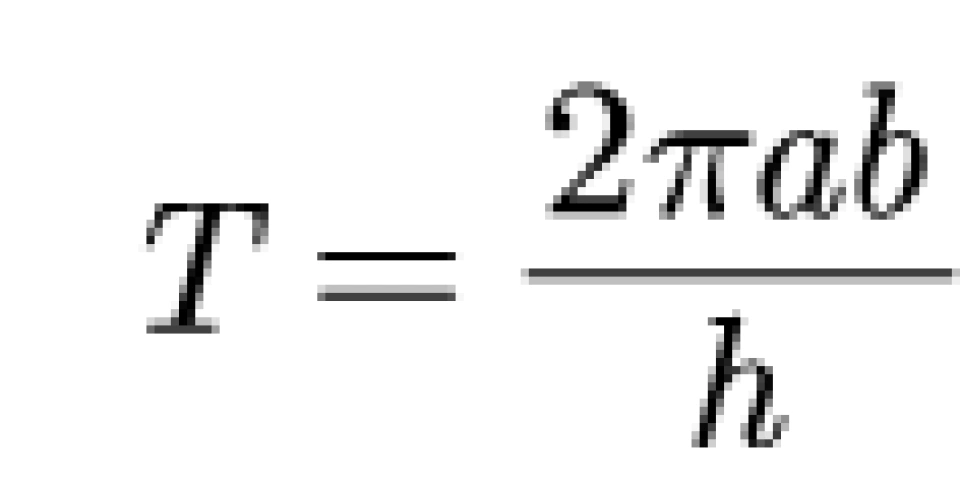
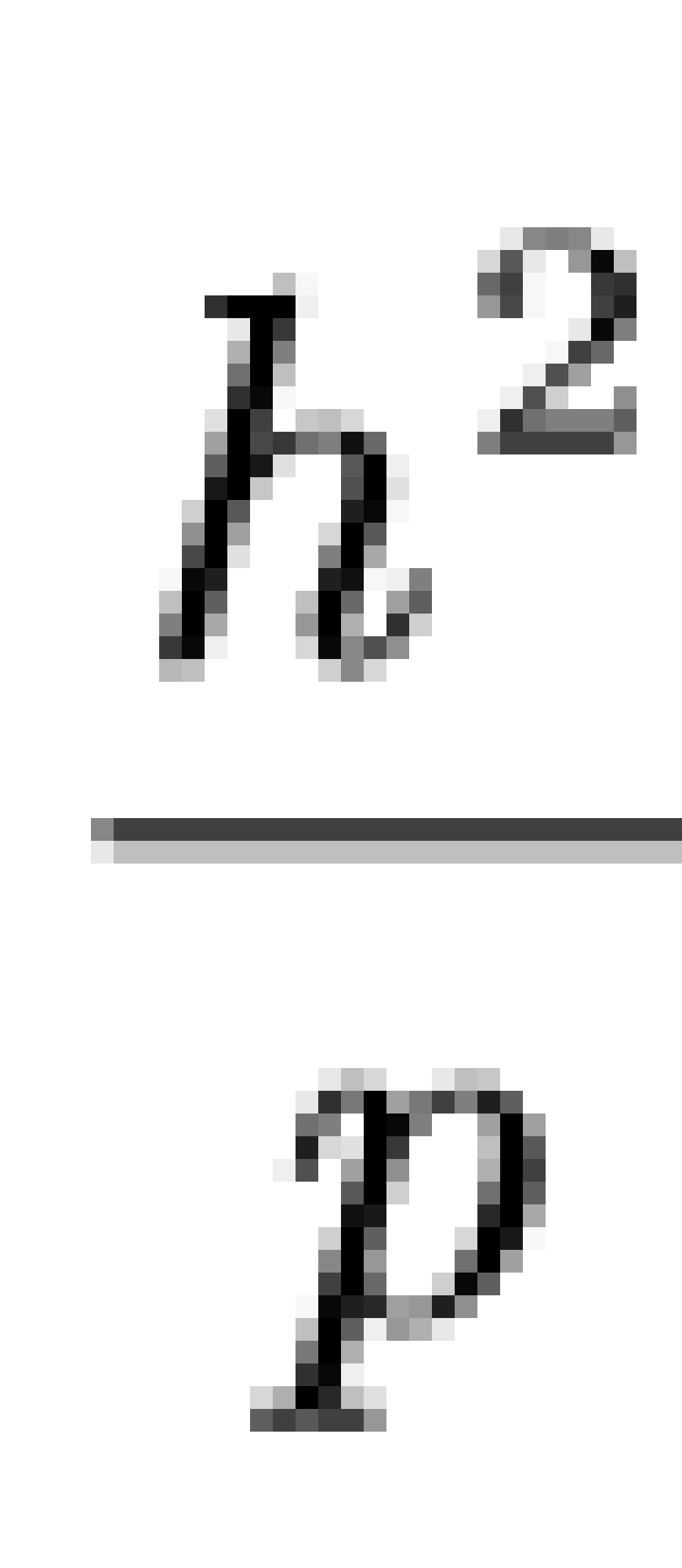
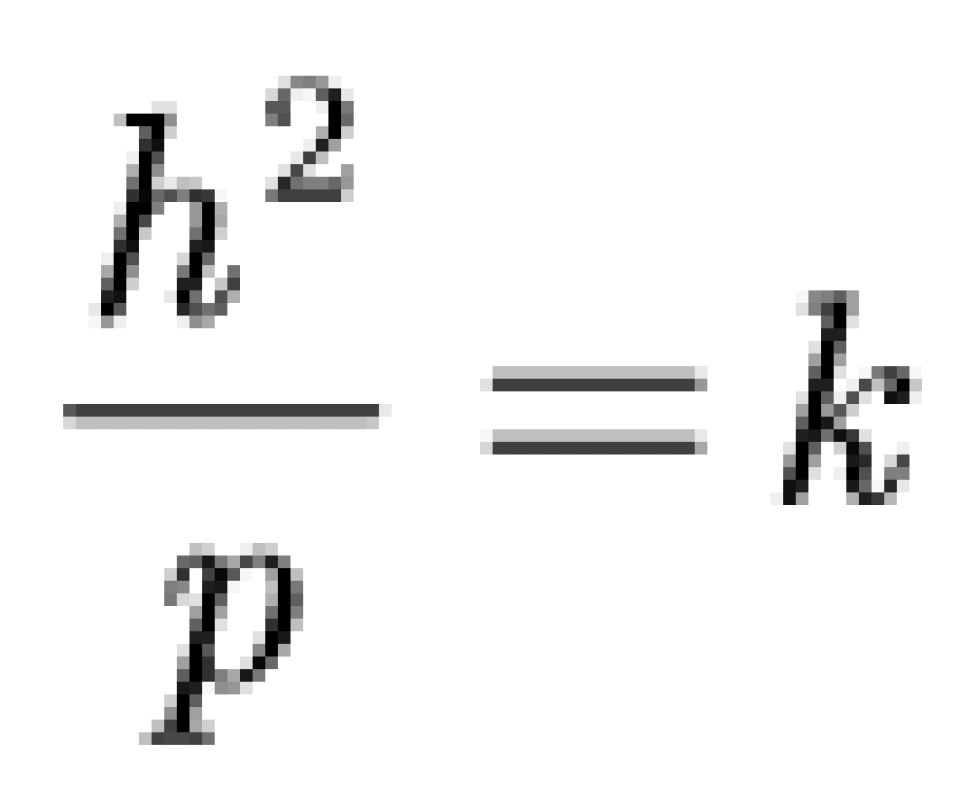
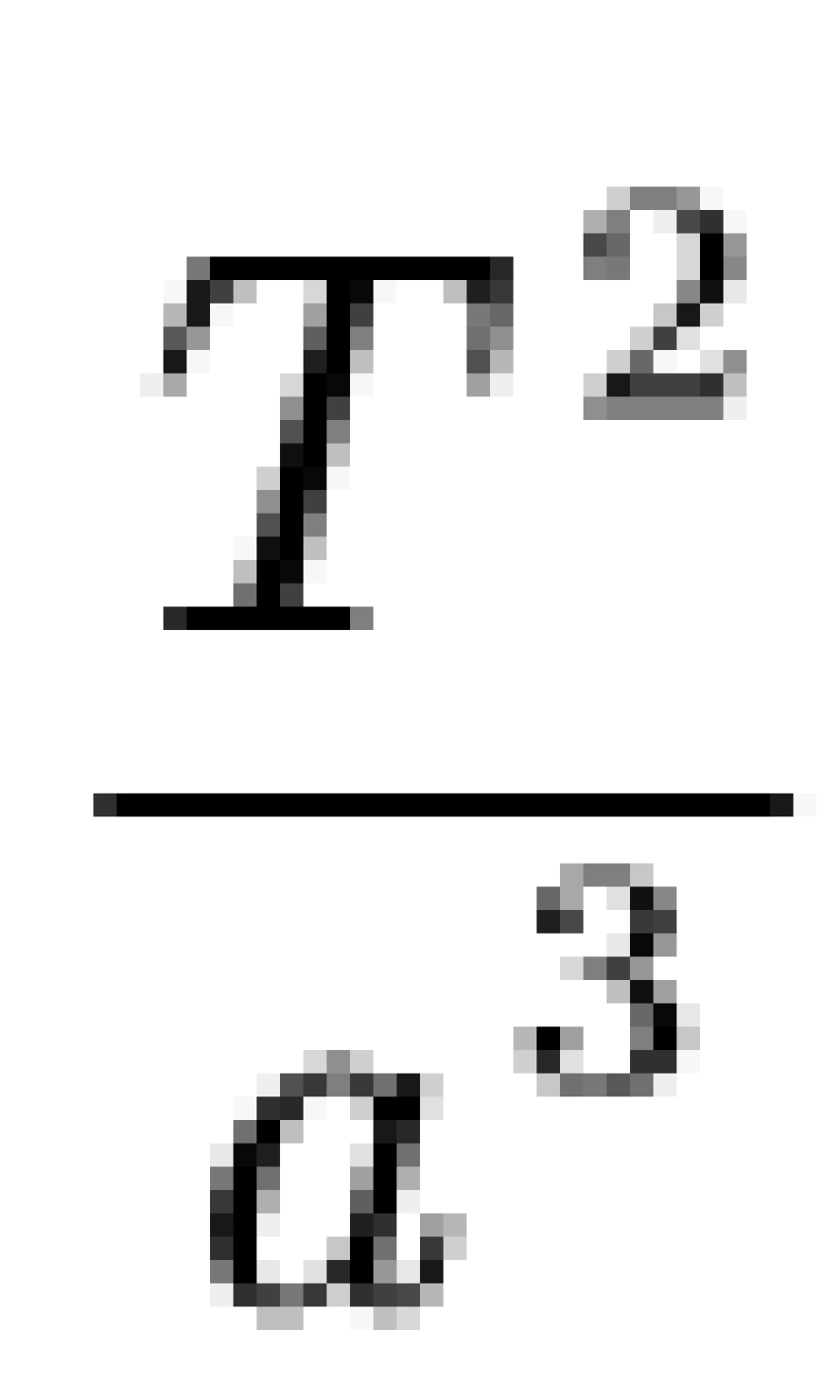
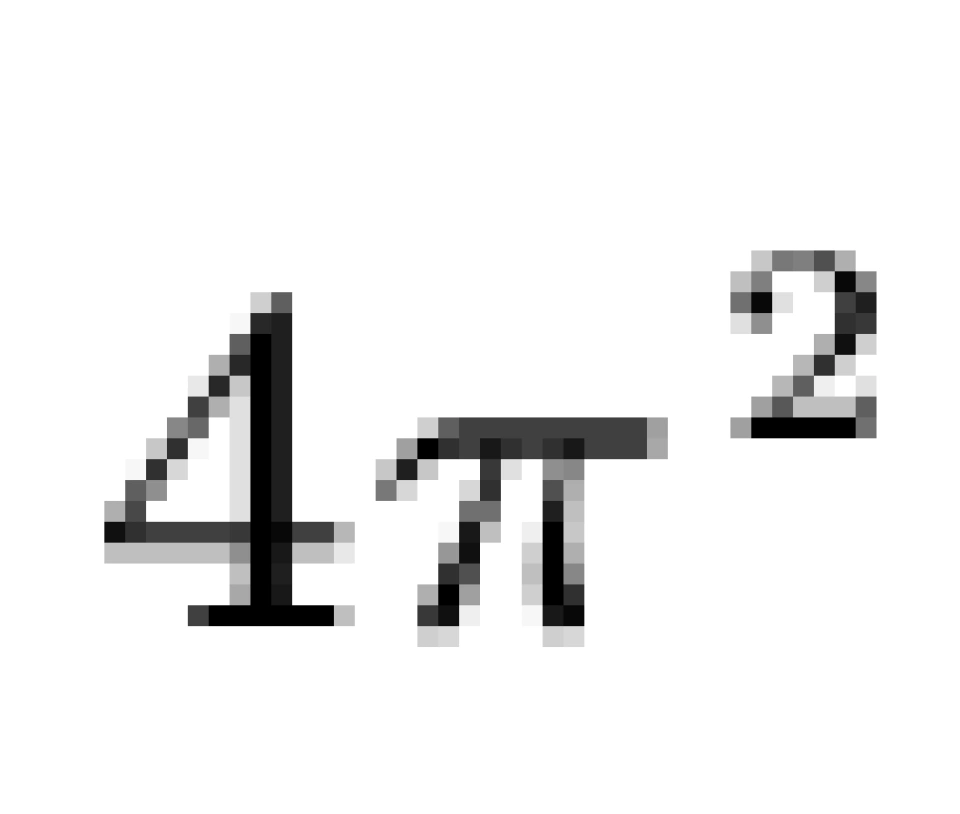
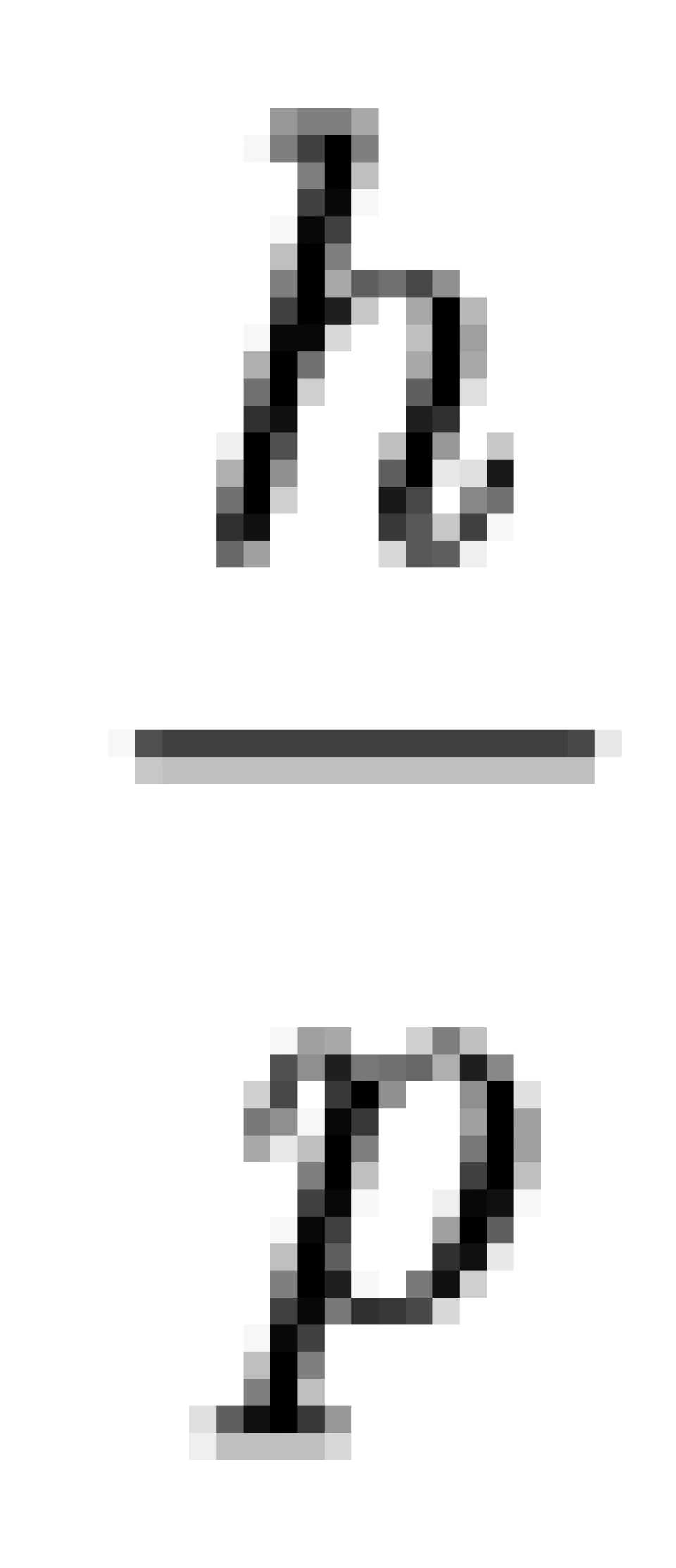

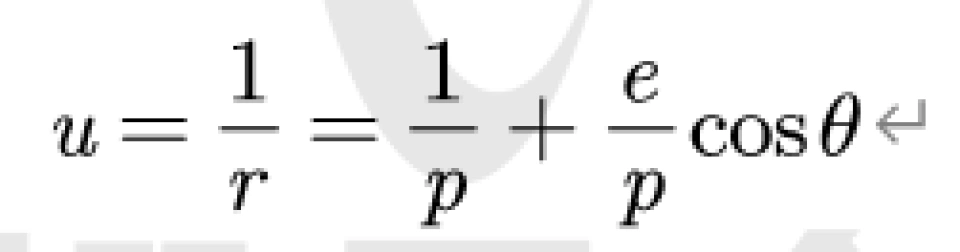



![[s-70]](https://www.bokeyuan.net/pic/image/emoji/cas/70.png)
![[s-2-7]](https://www.bokeyuan.net/pic/image/emoji/symbol/7.png)











