科普驿站 第四十三至四十四期
科目：数学
难度：B2
讲师：GHOSTS
上 2020.1.29
万有引力定律作为17世纪自然科学最伟大的成果之一，第一次解释了一种基本相互作用的规律，在天文学和宇宙航行计算方面有着广泛的应用。我来简单介绍一下万有引力定律的历史，这要从1665年英王查理二世复辟，伦敦发生大瘟疫说起——
为了躲避瘟疫，牛顿不得不中断在剑桥大学的学业，回到英格兰东部的乌尔斯索普庄园，随后就有了著名的牛顿和苹果的故事，也就是这个著名的苹果启发了牛顿对物体加速落向地面这一现象的思考。他通过计算得出的引力大小随距离平方递减，从数学上间接地暗示了，引力是均匀地向四面八方辐射的。但由于早期的计算不够精确，可能是只用了开普勒第二定律，只能证明圆轨道，而不是椭圆轨道上的这种平方递减关系。
直到了17世纪70年代，罗伯特胡克提出的一系列阐释了有关引力的未加量化的假设——所有天体运动都是引力作用的结果，天体本身也会吸引其他天体，并且距离越近引力越大。
在1679年到1680年的那个冬天，牛顿与胡克就引力问题互通信件，这使得牛顿重燃对于引力关系的兴趣。但他害怕自己的成果公开后，可能会遭到一些喜欢吹毛求疵的人的指责，就正如牛顿自己所说的那样——“我羞于将任何可能引起纷争的研究成果公开发表。”
《原理》一书能顺利问世，与埃德蒙哈雷的贡献密切相关。他曾于1684年询问牛顿：一颗遵循平方反比律的行星是如何运行的？（所谓的平方反比律，是指物体或粒子的作用强度随距离的平方而线性衰减。）牛顿肯定地回答，“似圆形”，并说自己在这方面的计算早到堪称成年往事了。从那时起，哈雷成为牛顿最忠实的支持者，其不断的督促和财务上的慷慨支持，使得牛顿答应他将万有引力方面的成果整理出来。牛顿暂停了手头上正在进行的包括古典数学、神学和炼金术在内的研究，利用当时更为精确的地球半径等数据，证明了地月之间的轨道吸引力遵循平方反比率，并且这种力直接导致行星以椭圆形轨道运行，这与开普勒的发现相一致。
牛顿利用欧几里得几何的方法，其证明过程中微积分只涉及到无穷小代换，因此本次介绍采用微积分的推导方法，也是现在比较主流的推导方法。
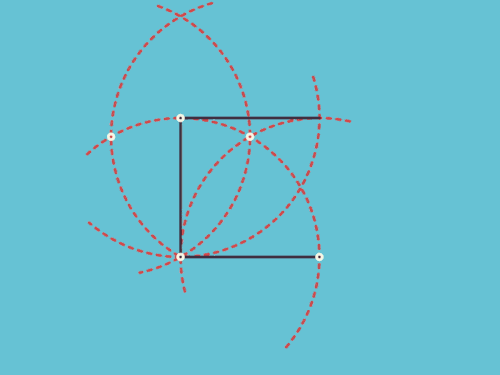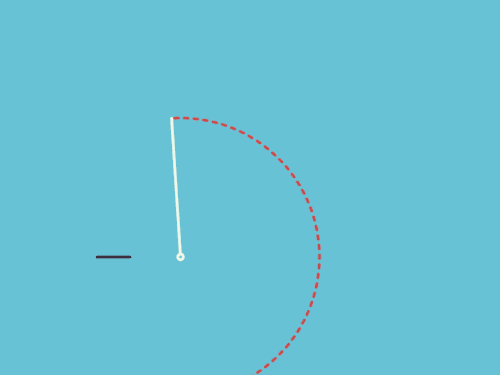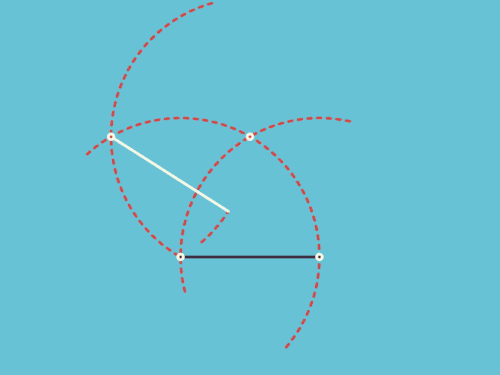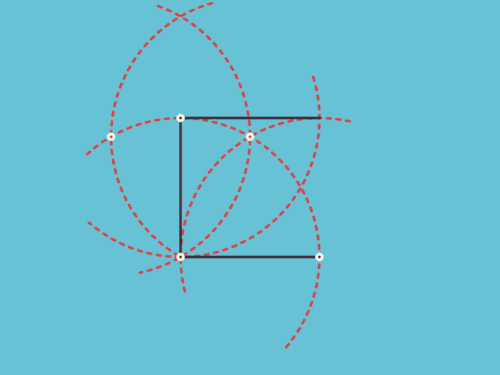
先介绍一下中心力场的公式：
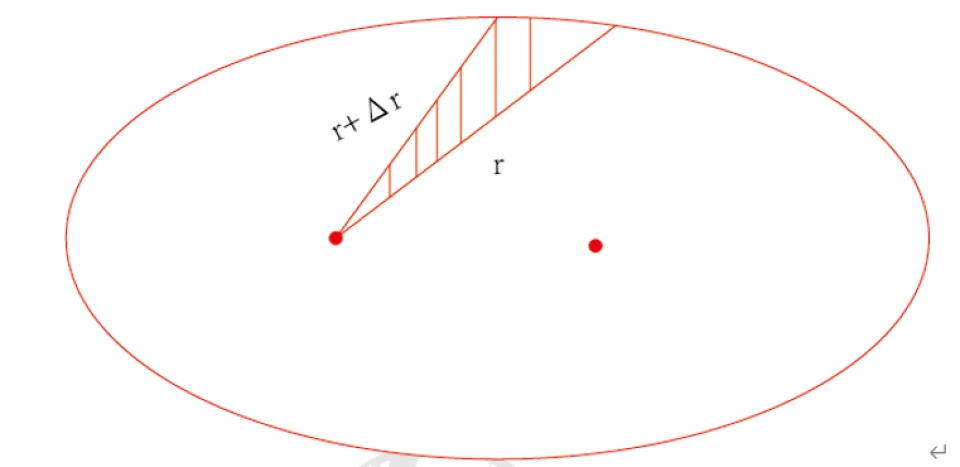
中心力场公式是由开普勒第二定律推到而得，也就是面积定律——在相同的时间内扫过的面积相等。
这里的c指的是常数，然后πab除以T，其中的πab指的是椭圆面积。这里要注意的是，面积之所以是1/2的那个公式，是因为我们将这一小段面积看作扇形。根据这个定律，我们就可以得出接下来的公式：
这里之所以令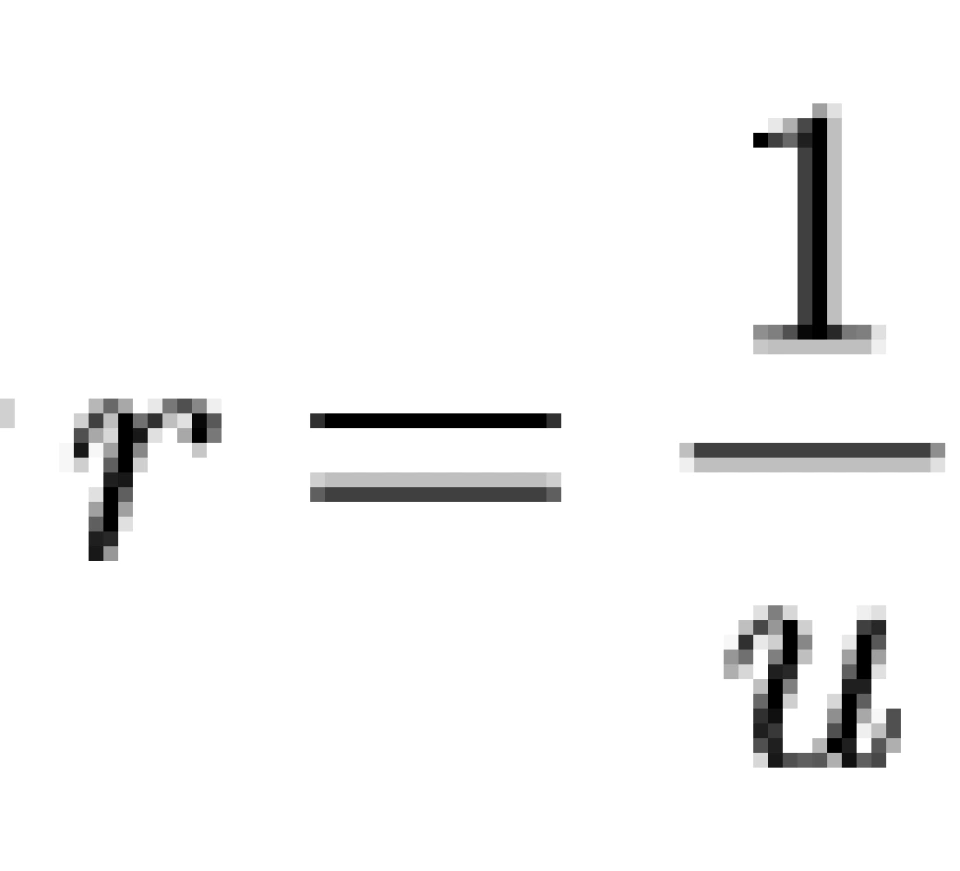
，是因为在从结果来往上推导的过程中，我们发现这么代换一下会使得结果更加简洁。而这里面的J是作为常数，因为不涉及角动量和求转动惯性。
这个就是推导
的过程。
其中的a部分就是将
代入；
b为正常推导；
c是因为
；
后面的d和e式子就是化简就行。
现在计算dr和dt的二阶导：
这里面要注意的就是b部分，是把前面一步的一阶导结果代入，还有d部分是代入。
通过这两个计算得出来dr和dt的一阶导和二阶导，代入可得：
再将
代入得：
这就是比耐方程的推导。
以下补充几点关于字母与符号的含义：
F：力
m：质量
r：径向距离
C、J：常数
R（开普勒第二定律）：径向距离
S：面积
【本文为耀星会的原创作品，未经允许，禁止盗用、转载、篡改文章，否则耀星会和作者将追究版权责任。】
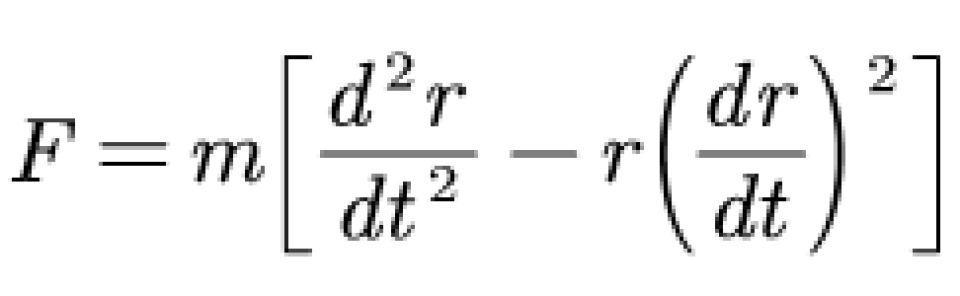
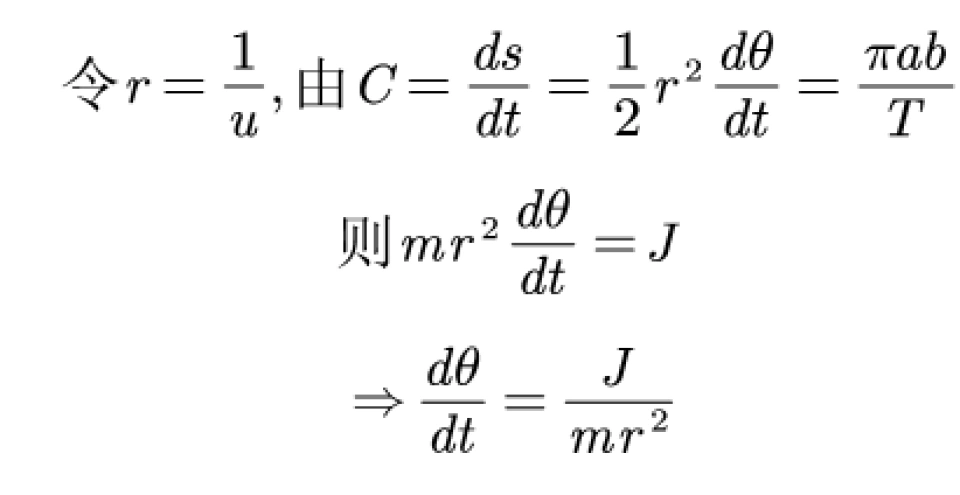
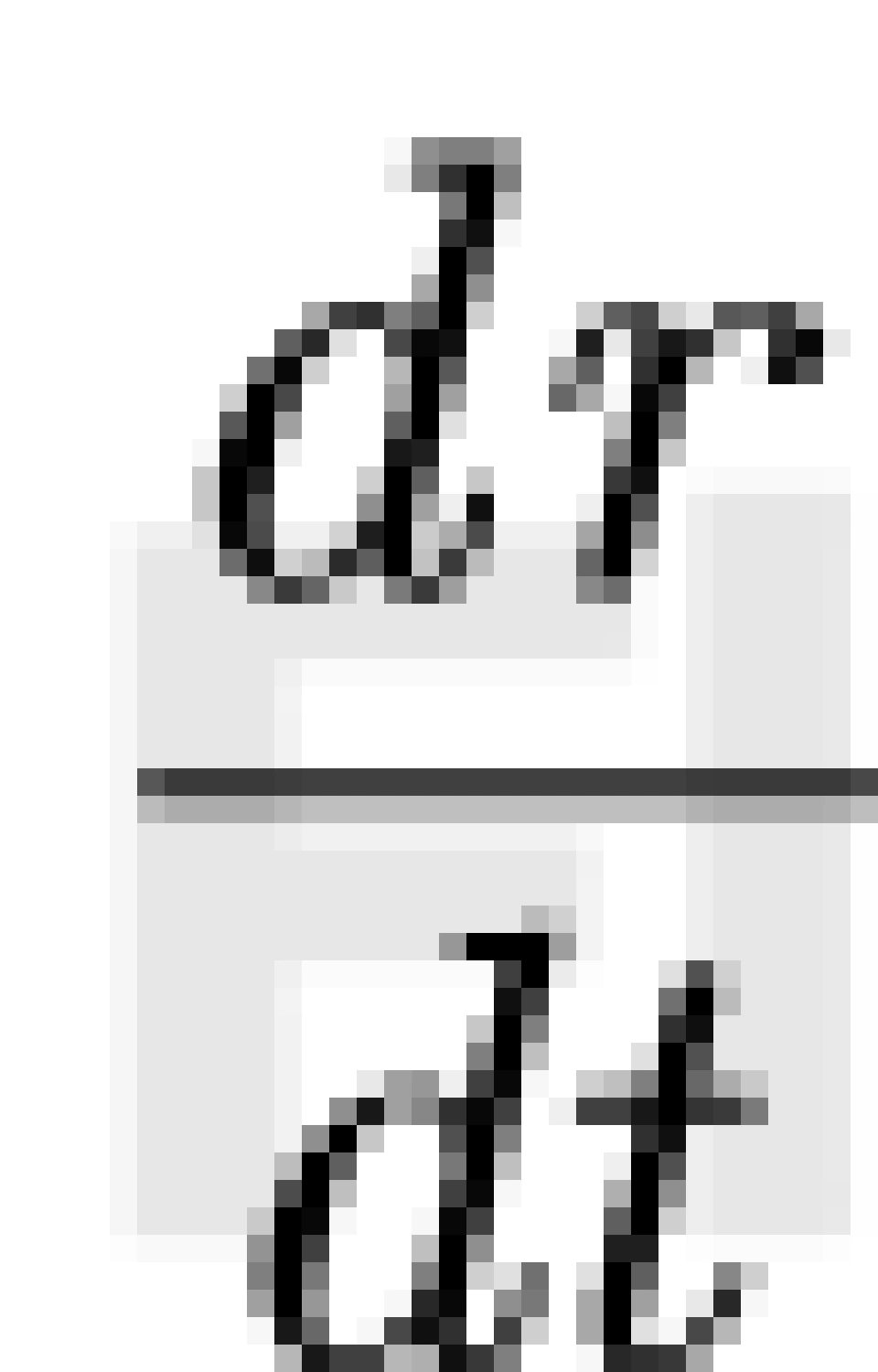
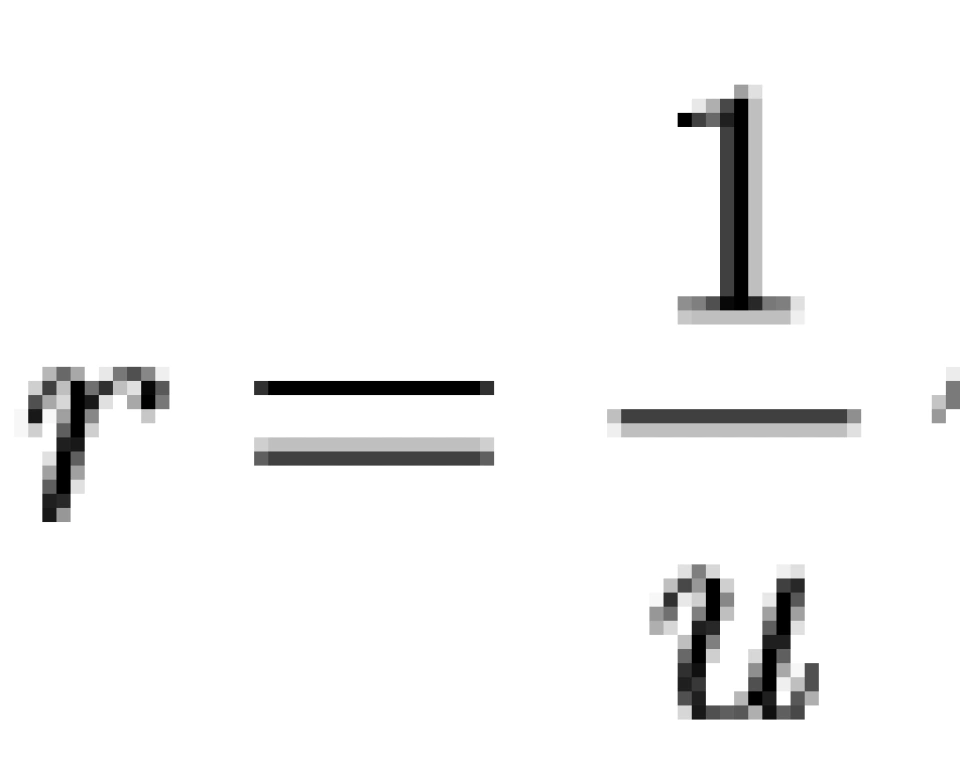
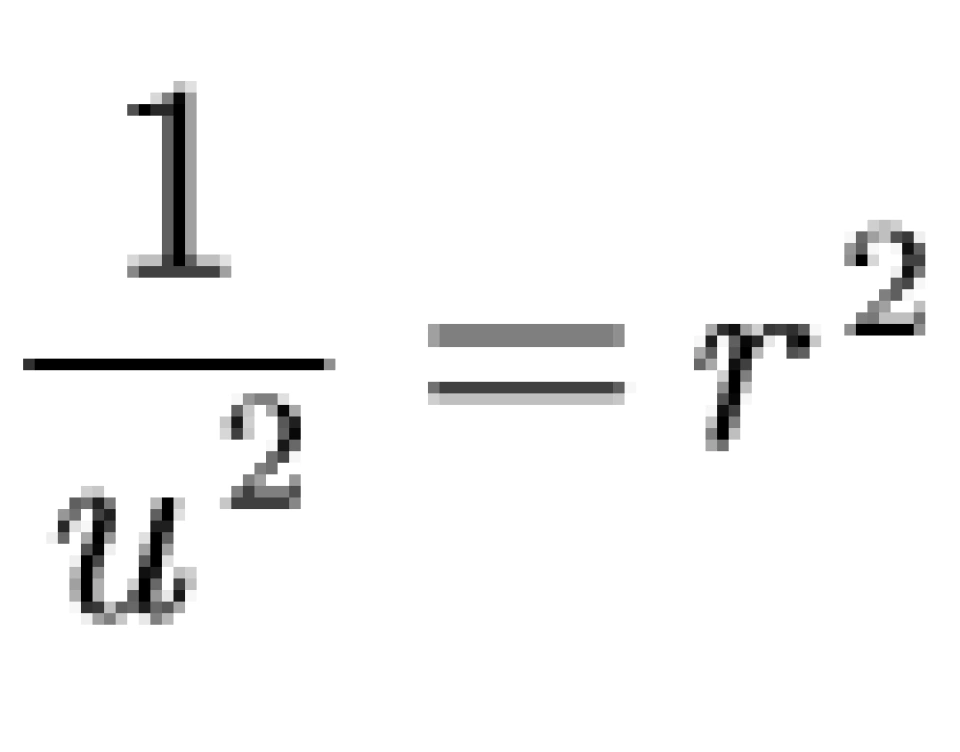
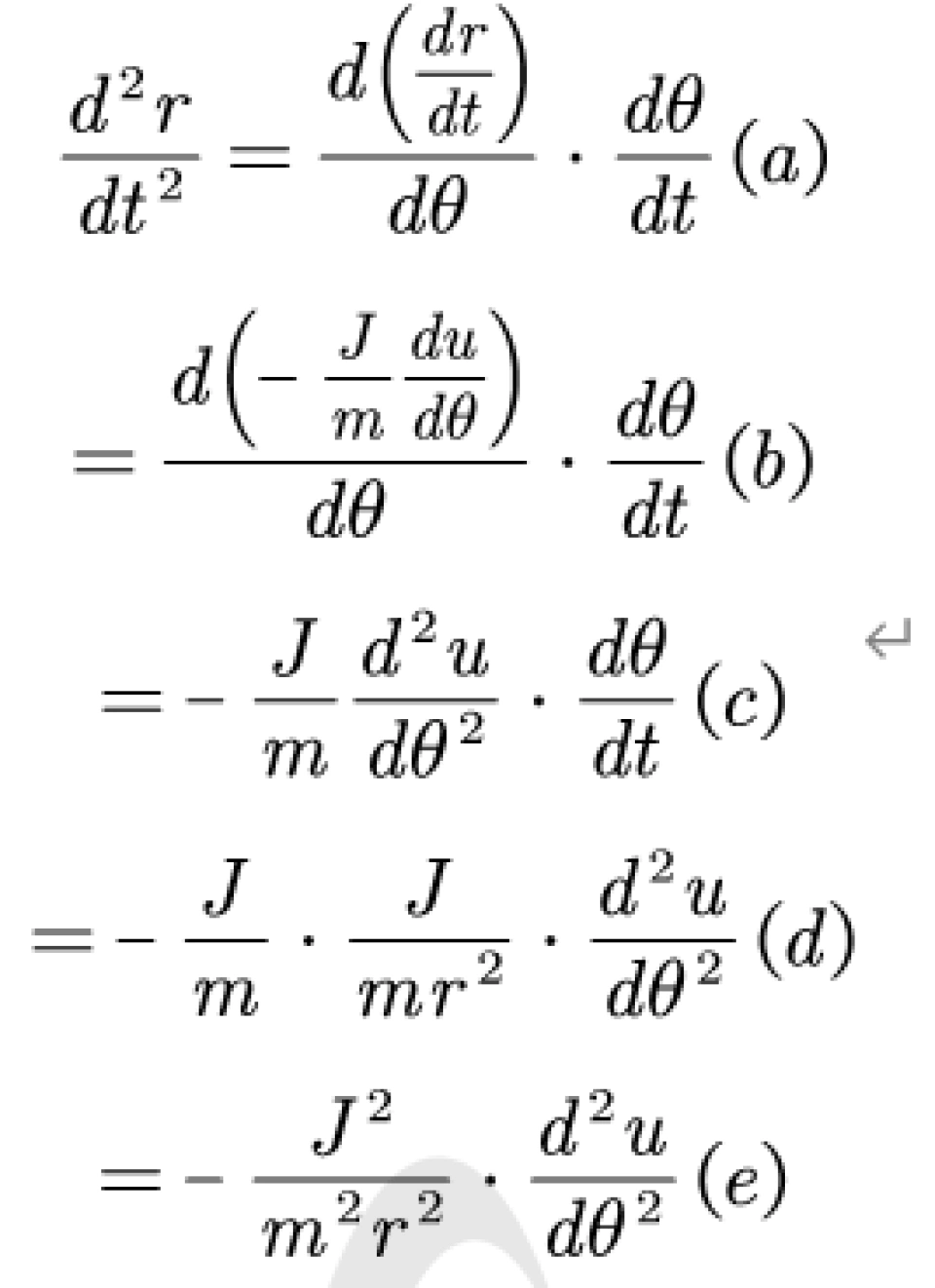
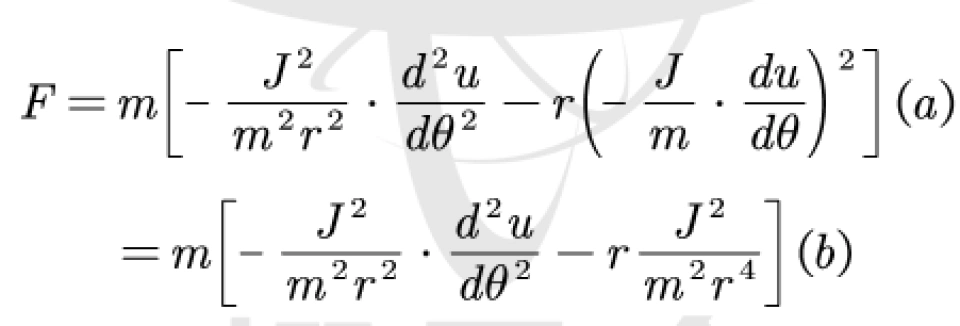
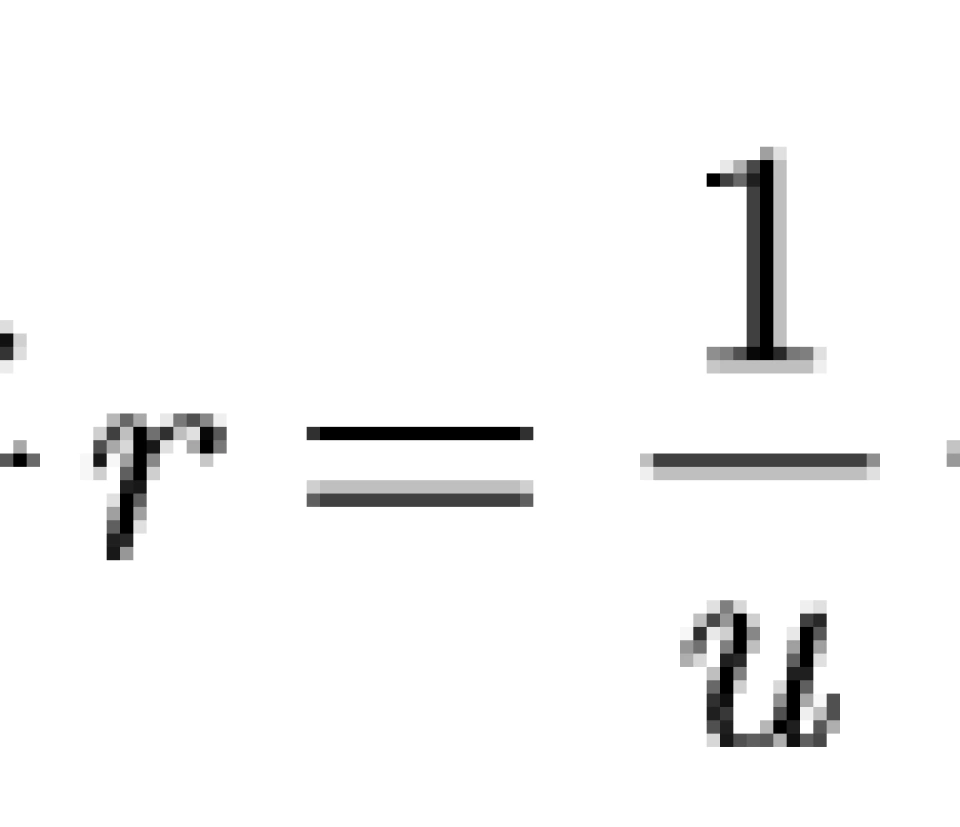
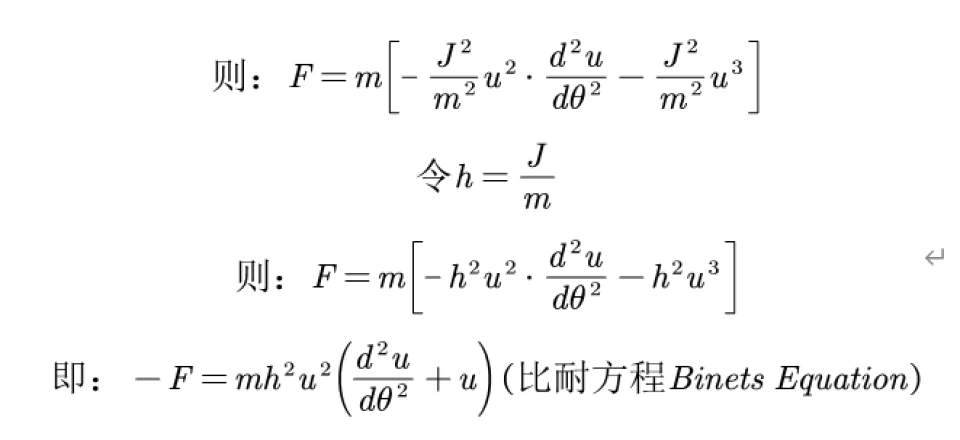
![[s-70]](https://www.bokeyuan.net/pic/image/emoji/cas/70.png)
