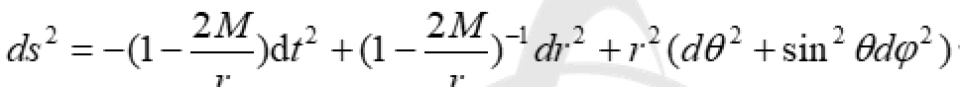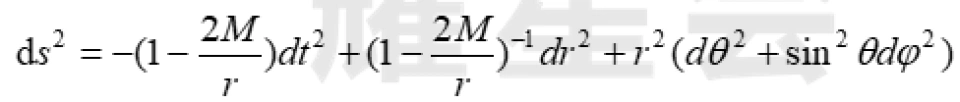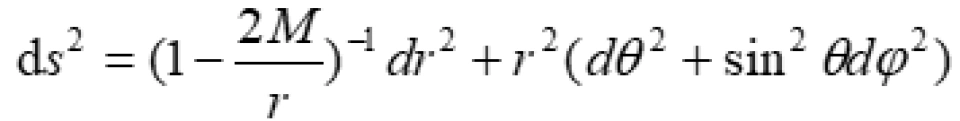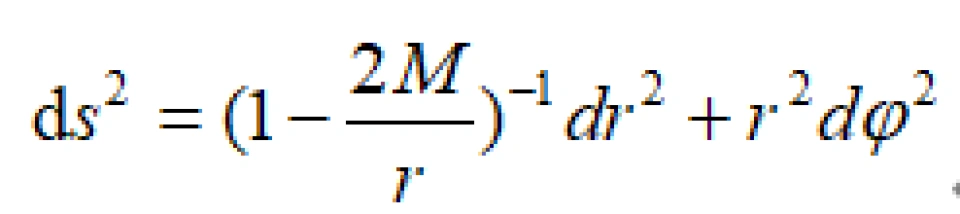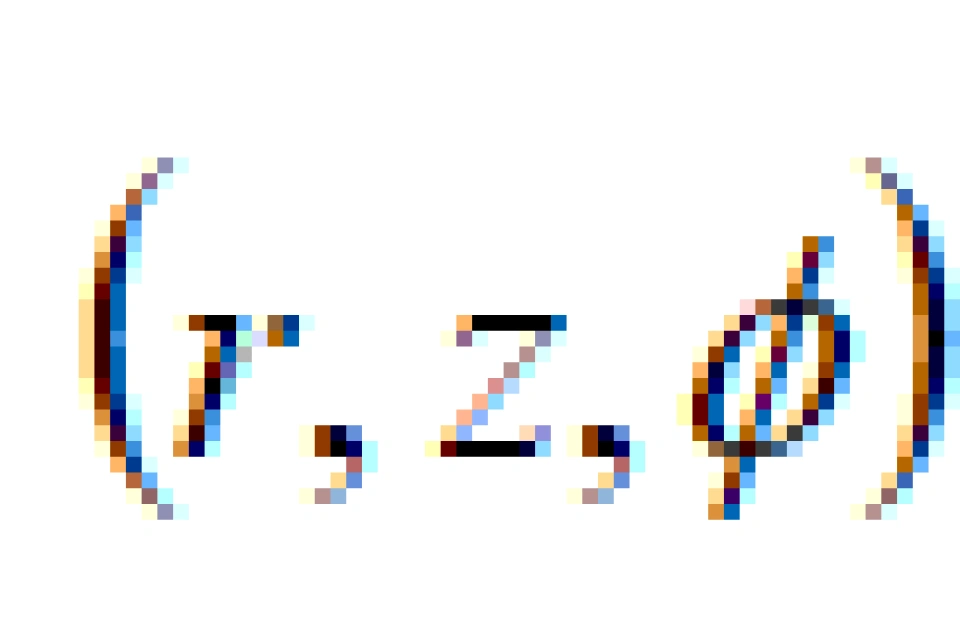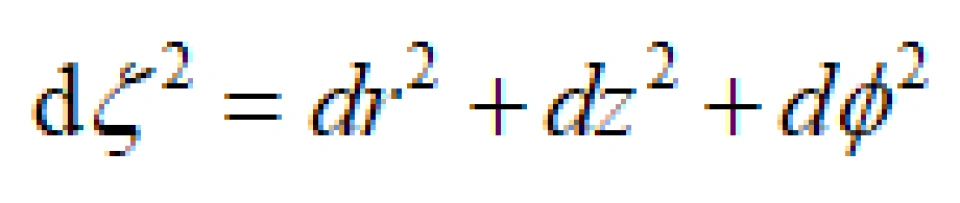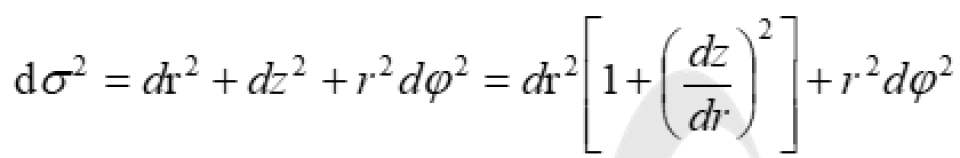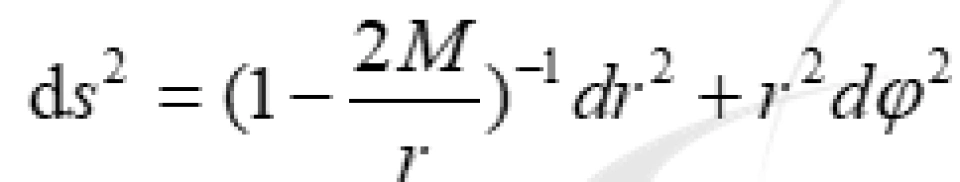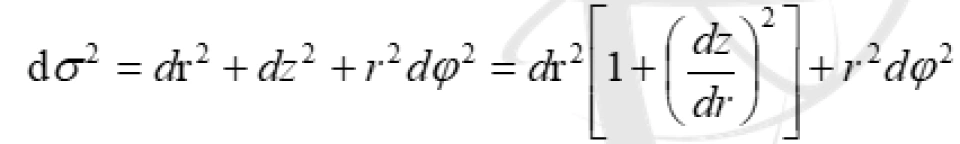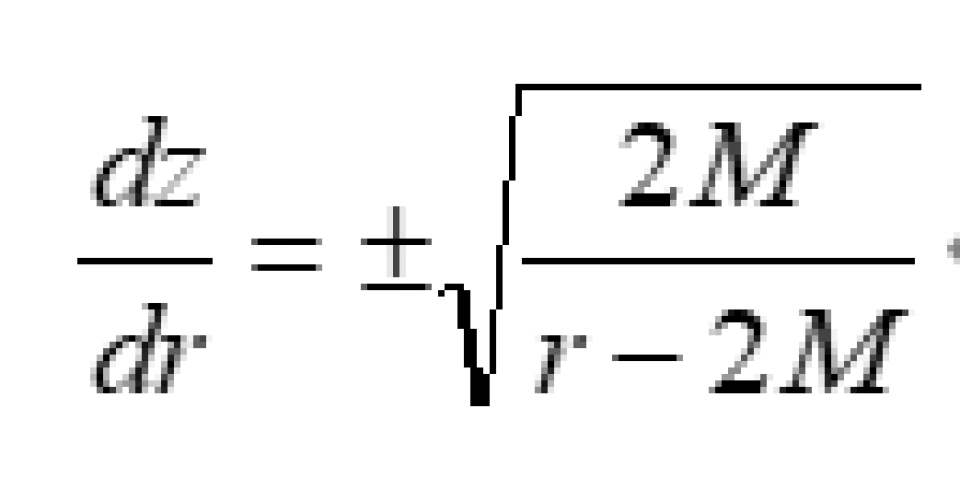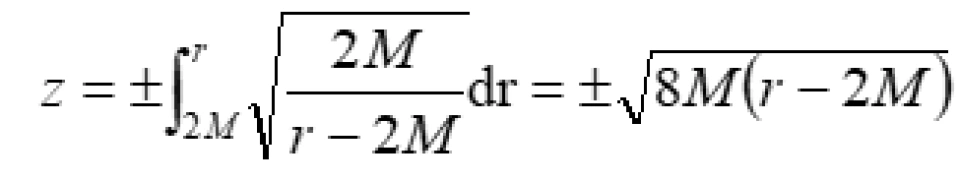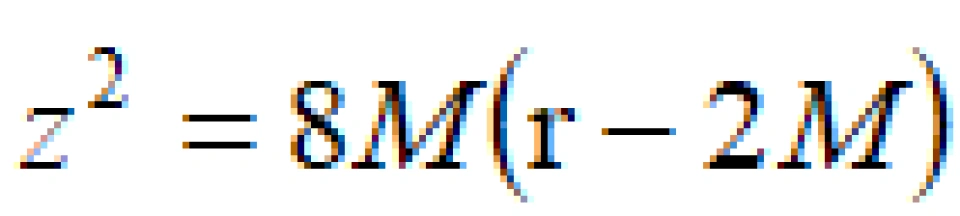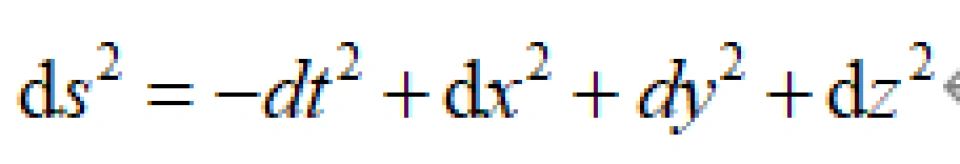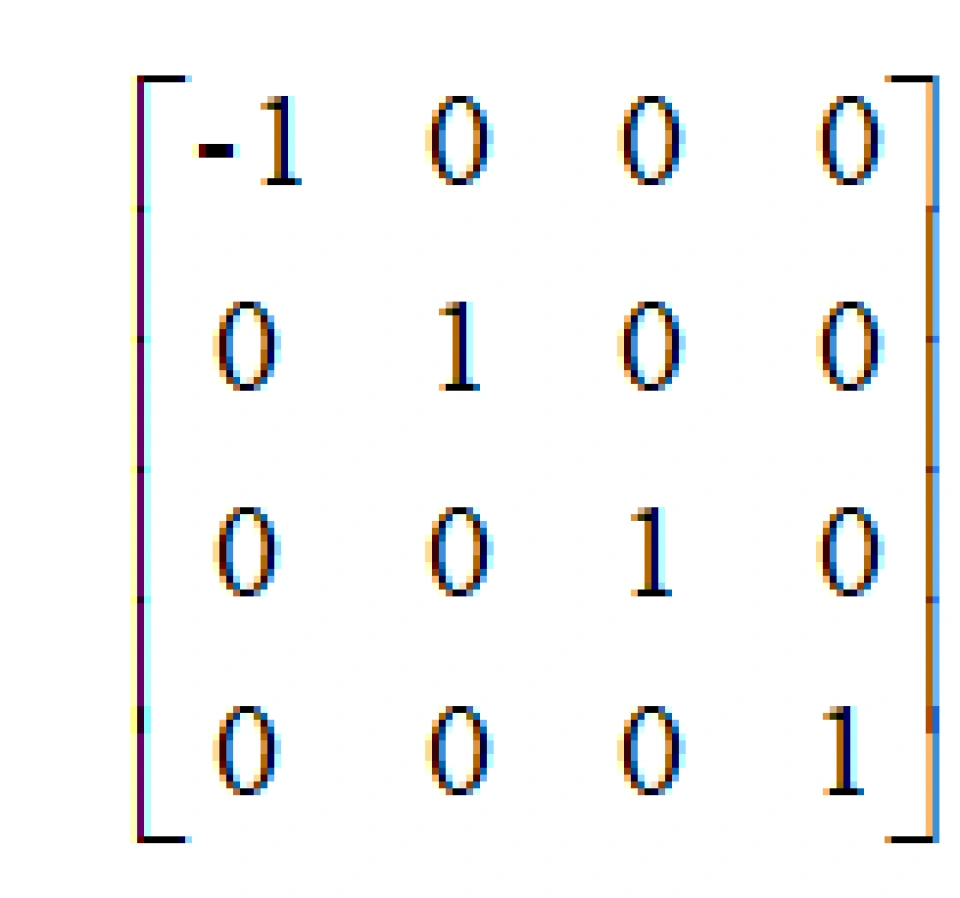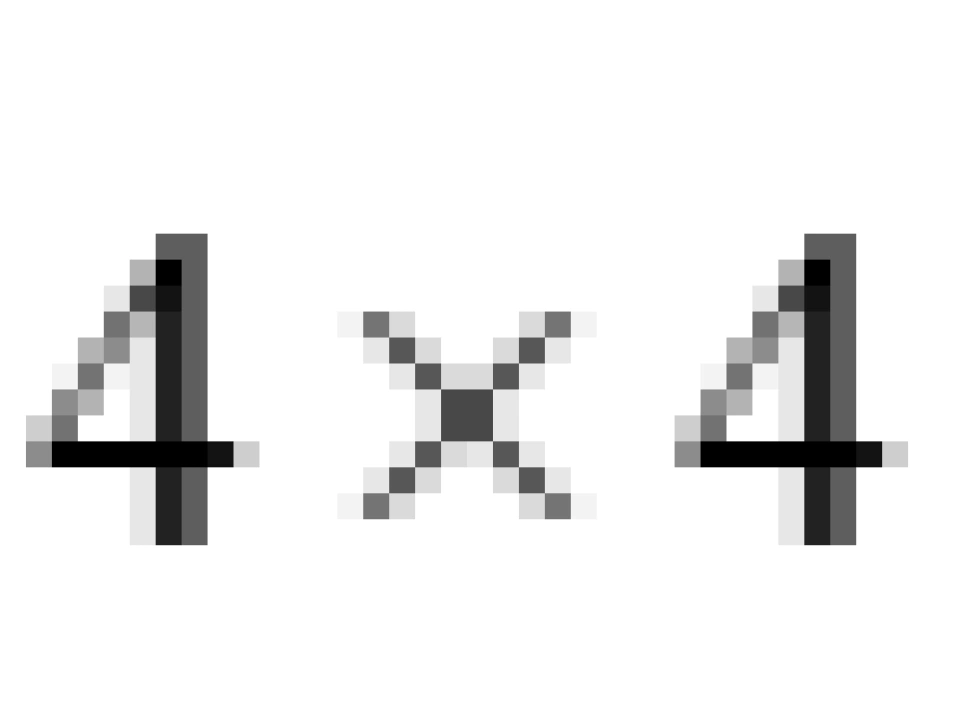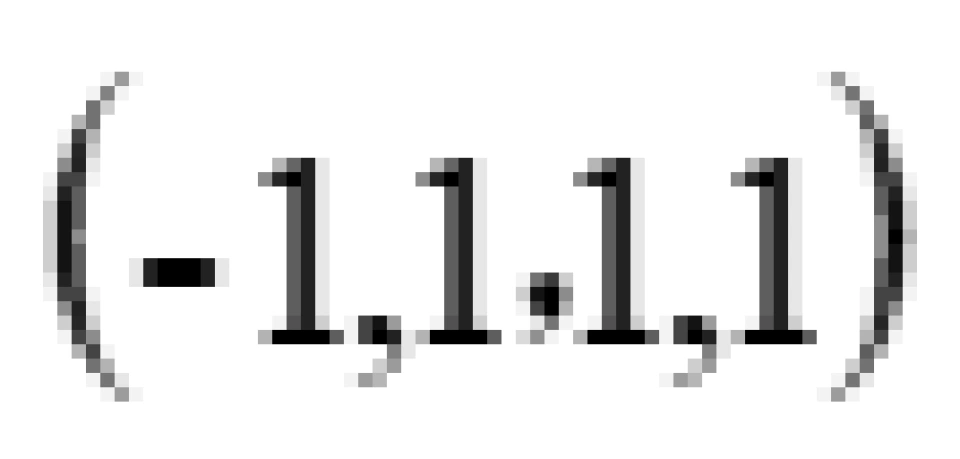科普驿站 第三十九期
主题：时光机与任意门（第一期）
难度：B2
讲师：弦轴子
接上期内容，还可以考虑一些特殊情况，比如假设一颗天体没有自转，静态，它的引力场具有球对称性。有了这些限制条件就可以大大减缓难度，可以把方程的解求出来。我们可以将直角坐标系的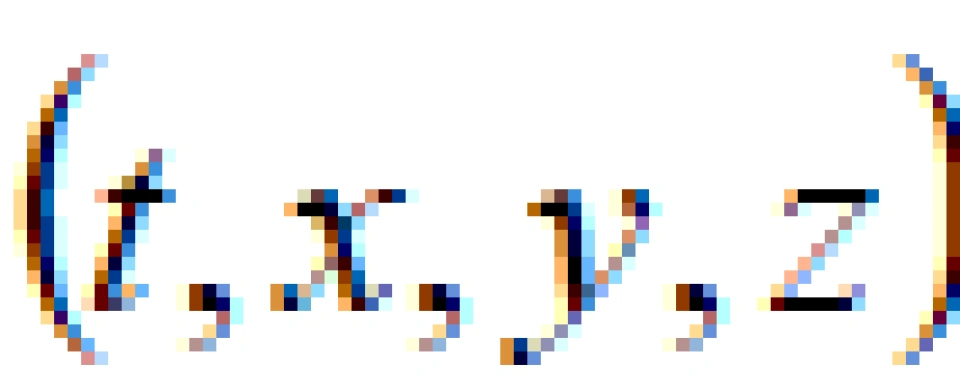
改成采用球坐标系
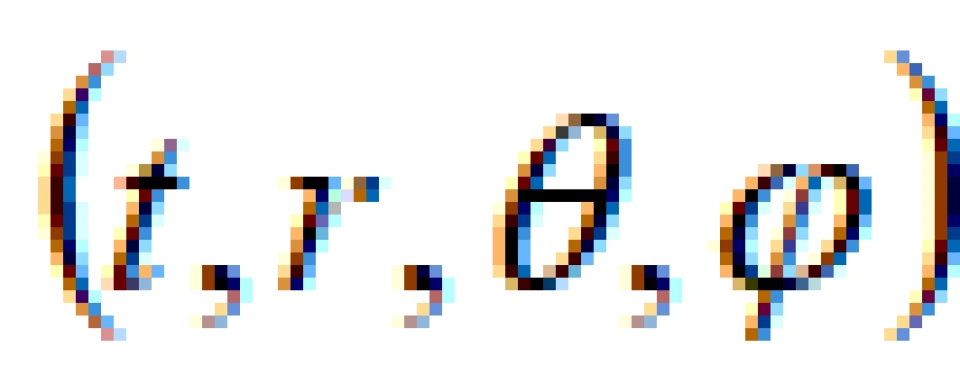，这样更容易看出球对称性。
这样我们将会得到一个解一一史瓦西解（应该是第一个最精确的场方程的解）。它是描述静态没有自转而且具有球对称性的时空。但是它分成了两部分，就一种是天体内部的，还有一种是外部的真空解。
我们得到的球坐标系下的史瓦西时空的时空度规线元是这样的：
时间项分量的系数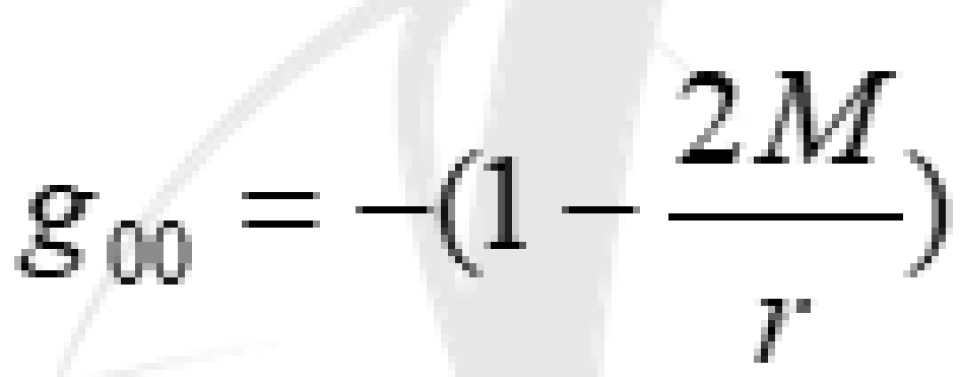
，当
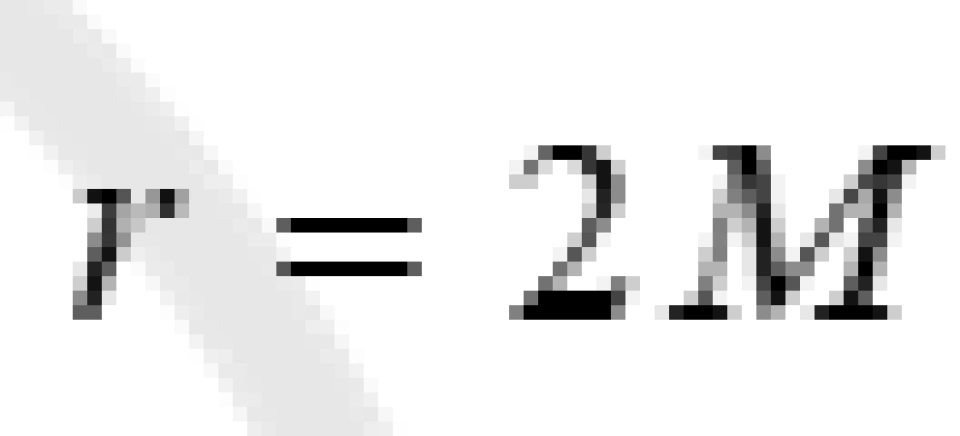时，这一项分母将是零。
不过现在我们考虑的是静态时空，时空度规不含时间亦即：t为常数。
这样，我们再看一下球坐标系下的史瓦西时空的时空度规线元，如下：
静态时空，球坐标系下的史瓦西时空的时空度规不含时亦即t为常数的时空度规线元是这样的：
它其实是t为常数时，三维空间的度规。不过，由于空间的球对称性，我们只需研究赤道面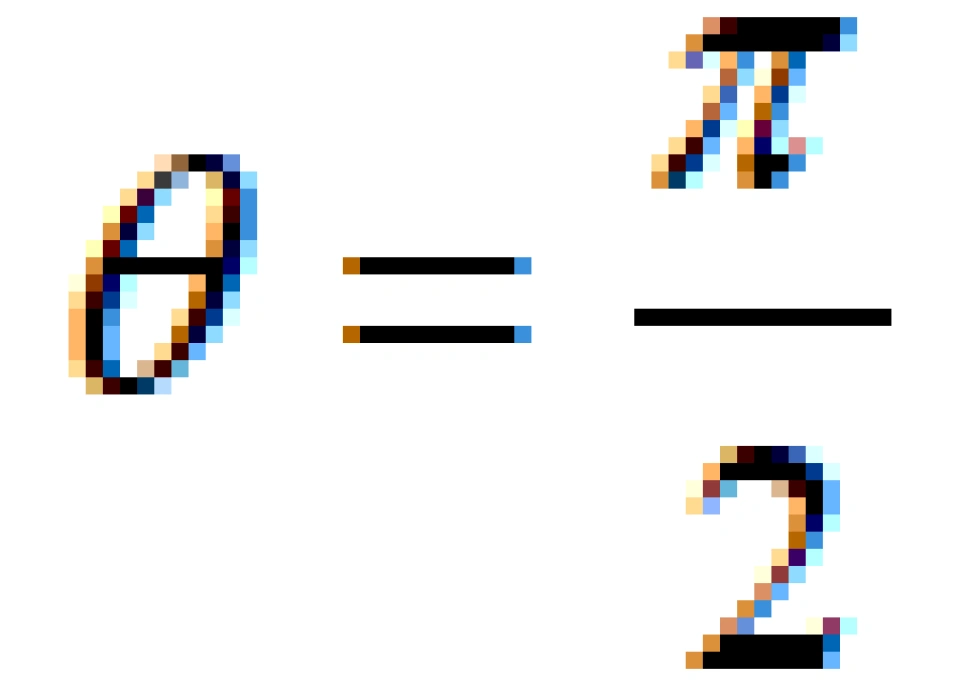
时的情况（读者不妨想想为什么可以这样做）。
亦即：
然后我们取一个普通的欧式空间，采用柱坐标系
，
那么它的空间线元就是：
，很显然这就是普通的平坦空间。
我们把时间为常数时，史瓦西三维空间镶嵌在这个欧式空间，就可以得到这个：
我们比较
和
可以得到一个很简单的微分方程：
这是一个很简单的微分方程，它的解就是：
最终我们可以得到：
它是描述一个回旋抛物面，它是跟史瓦西时空时空解在某一固定时刻（t为常数）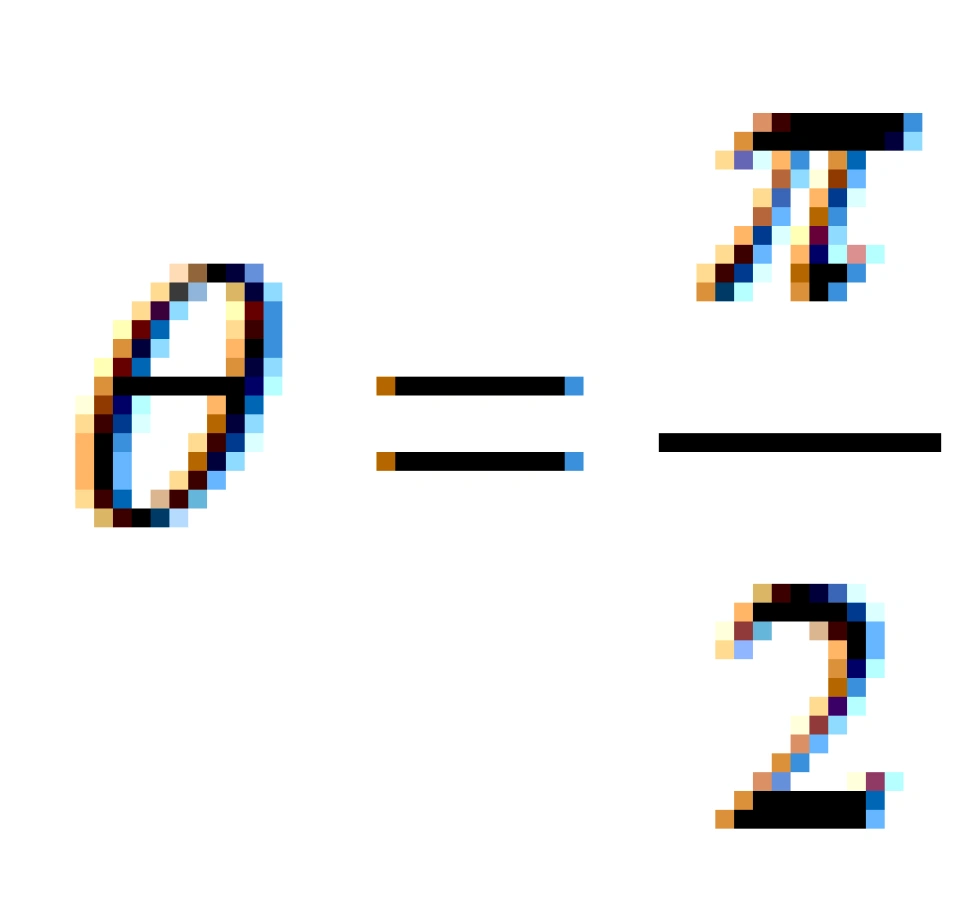
时的几何结构相同。因此，我们把这几种几何结构图称为史瓦西时空的嵌入图。
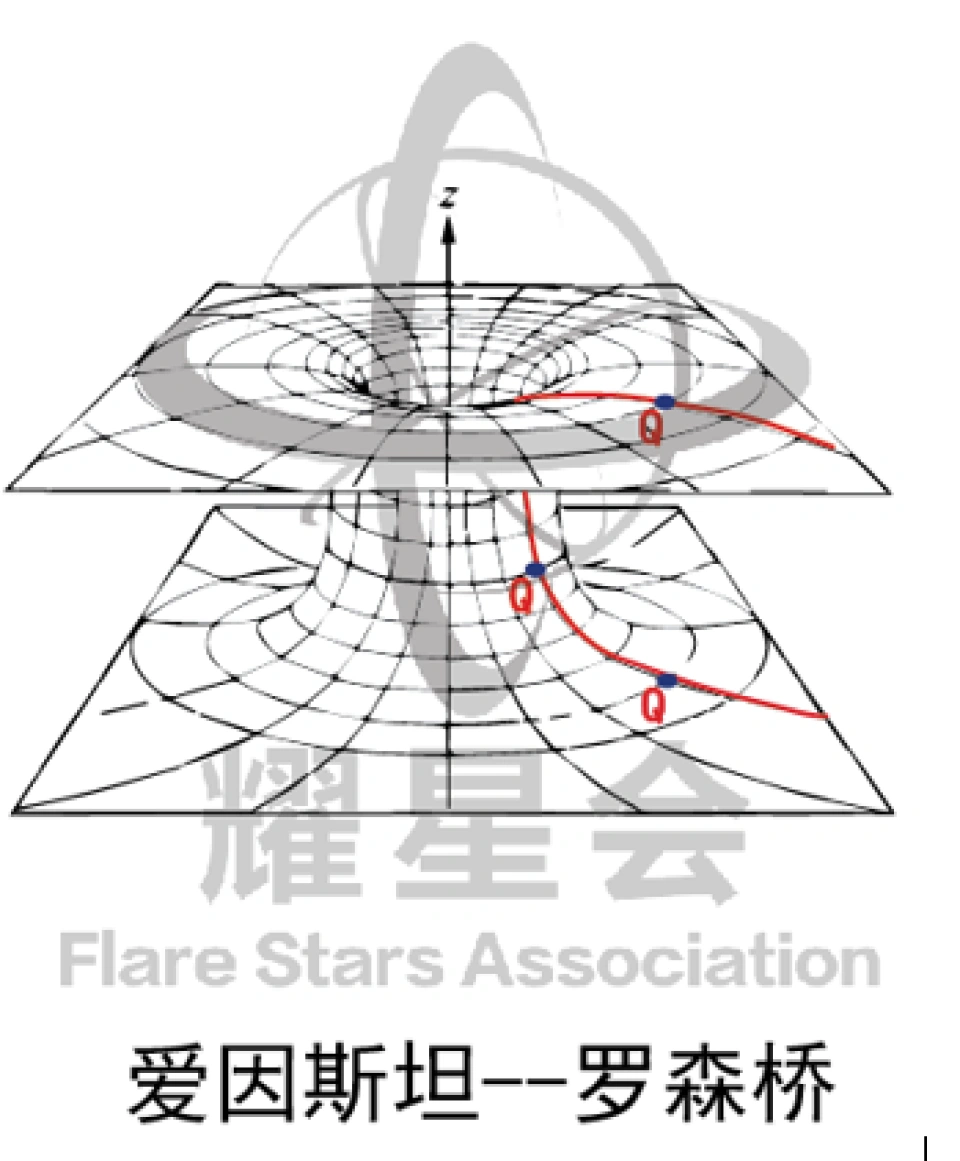
（下面这张鬼样）
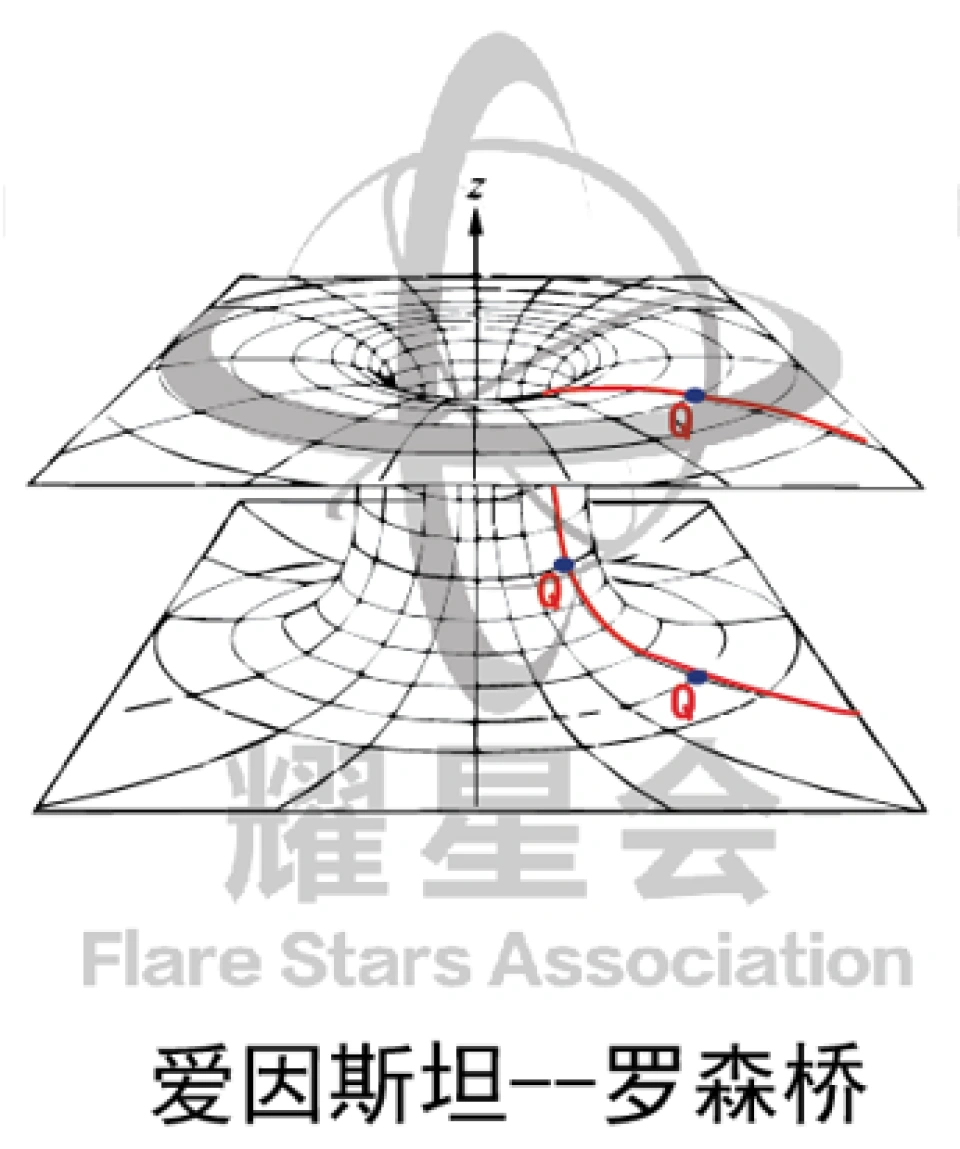
这里注意的是，这张图是降维描述的。我们三维空间对应着的其实是二维表面。
上面那个Q点和Q'点代表物体的位置，我们穿过这个虫洞，其实是沿着这个二维表面的曲线，并不是中间那个空洞。
上面的洞口叫做黑洞，下面的洞口叫做白洞，中间的管道就是虫洞。
事实上虫洞也没有这个管道空洞，由于是降维描述，所以你在这张图看到的圆形其实是球体。
中间的喉部包括洞口的圆形也是这样，都是球体，但是我们在图纸上很难表达出来。
那么这中间的洞究竟存不存在呢？它到底是不是四维空间呢？其实它什么都不是，它根本就不存在。它之所以存在，仅仅是我们为了直观表达虫洞这个图像而已。
不仅是虫洞，在广义相对论的框架中，任何弯曲的图像都不需要借助更高维度，但是当我们想直观的表述出来时，就需要借用嵌入更高维度的方法。
这里我们简单说一下到底是怎么回事。
广义相对论中时空弯曲到底是怎么回事？
在广义相对论中，时空就是四维流形附带时空度规。
这个流形可以简单理解为同胚或者等价于局部的相同维数的欧式几何。
这些东西是由黎曼推广来的，而黎曼的工作就在高斯的基础上发展了。
说到高斯的工作，我们先谈谈一些题外话。
现实中一根曲线无论怎么去弯曲，我们都可以把它掰直，并且不改变任意两点之间的距离换句话说就是不会扯断它。
对于圆柱面也是这样，我们可以把它展平，也不改变圆柱表面任意两点之间的距离换句话说就是不会让表面发生拉长和压缩。展平一个曲面的前提就是必须是等距变换。曲面任意两点的距离要保持不变。
但是你有没有发现对于球却不可以。而且我们画世界地图需要两张才可以！
这个时候就有小朋友抬杠了，我家世界地图是挂一张可以。涵盖整个地球。可是你没有发现你这张世界的时候有什么不同？这些世界地图都是投影所画，所以有些地方是有所出入的。
真实的情况下，球面不可能展开成一个平面。这样会导致球面任意两点之间的距离会变化，也就是拉长或是压缩球面，从而改变球面上任意两点之间的距离。
因此关于这个现象高斯研究了很久，终于在1827 年的发了发表了一篇《关于曲面的一般研究》论文中，发展了内蕴几何。
何为内蕴？讲到这个概念就要讲到外嵌，我们平常说一个曲面弯曲或者一个圆柱表面弯曲或者球面弯曲，通常是从三维空间中角度去看的，这个时候我们就可以说这个球面或者是这个曲面的，他们是外嵌至三维空间中的。
那么有没有一种曲面，它是不依赖于把它置入三维空间中，而是从自身曲面自己的。几何结构出发去探寻寻找弯曲或者曲率呢？
当然是可以的。
首先，高斯研究曲面在一个给定点及其附近邻域的法线方向，定义了高斯映射。然后再通过高斯映射定义曲面的内蕴曲率。然后我们寻找这个曲率就可以了。
大概意思就是这样：
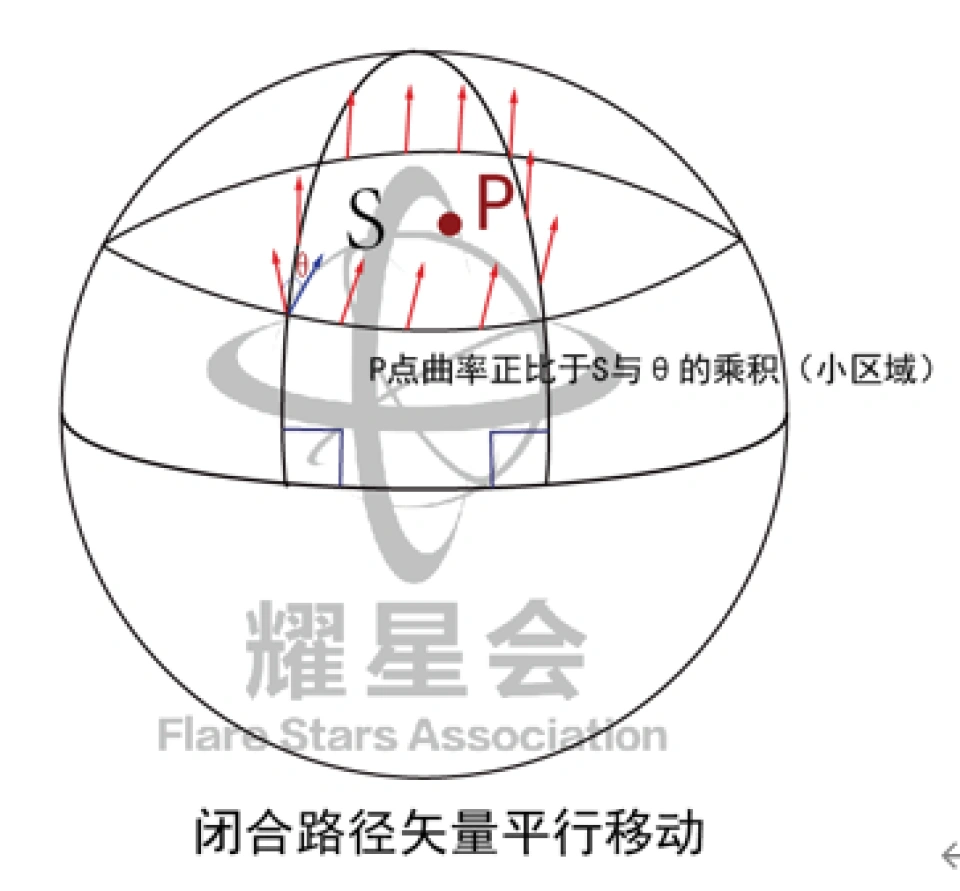
如上图所示，在曲面上任意找一个定点P，P点及其附近邻域的面积是A。过P点找一个垂直于此点的法向量和附近邻域上各点的法向量(垂直于这块球面区域的向量)。然后将这些法向量的端点全部移至某一单位球(半径为1的球）)的球心，但保持这些法向量的方向不变。这些法向量与这单位球球面相交的区域面积为B。
这就是高斯映射，是从某曲面到单位球面的映射。
高斯认为，曲面上点P的内蕴曲率正比于面积B和面积A的比值。也就是说，曲面在点p附近的内蕴弯曲程度可以由面积B和面积A的比值决定。于是高斯将这个定义为高斯曲率，它是衡量曲面在某一点处弯曲程度的，这个弯曲程度只和曲面的内部结构有关。
很显然，对于可展开的曲面，它是没有内蕴曲率的，因为他在单位球上映射是一个点，也就是面积B是0，所以，高斯曲率就是0。不信你可以找一个圆柱面去试试。
从此，弯曲再也不需要被置入更高维的空间去看，从这个曲面本身的几何结构出发就可以得到弯曲程度。
不过高斯主要研究二维曲面，至于三维曲面，四维曲面，更高维的曲面有黎曼来推广，把他们统称为流形。而描述这些流形的内在弯曲，黎曼是利用截面曲率来定义，将曲率推广为黎曼曲率张量。对于二维流形，则正好对应了上面我们介绍的高斯曲率(内蕴曲率)。
既然知道流形，那么什么叫度规呢？你就把它粗略的理解为在一个曲面上计算两点之间距离系数，并把它写成一个矩阵形式。至于矩阵，你就把它理解成一个具有一定规则的数组。
至于数组……
算了……
在数学上流形附带这种度规才是一个完整的体系，被称为空间。
而在物理上，只有附带的度规分量是一正三负或者是一负三正才被称为时空。
为什么这样规定的？让我们回到我们上面介绍的闵可夫斯基的工作。
闵可夫斯基从数学角度出发，发现了相对论的一个不变量，或者被称为时空间隔。他当时的想法是把整个四维时空当做一种几何，这个不变量就是这个几何上的任意两点或者是两个事件之间的距离:
显然，如果把它的系数写成矩阵的形式，也是数组的形式，是4×4的。
上面这个
矩阵的对角元就是
；这些对角元之和就是号差。
这个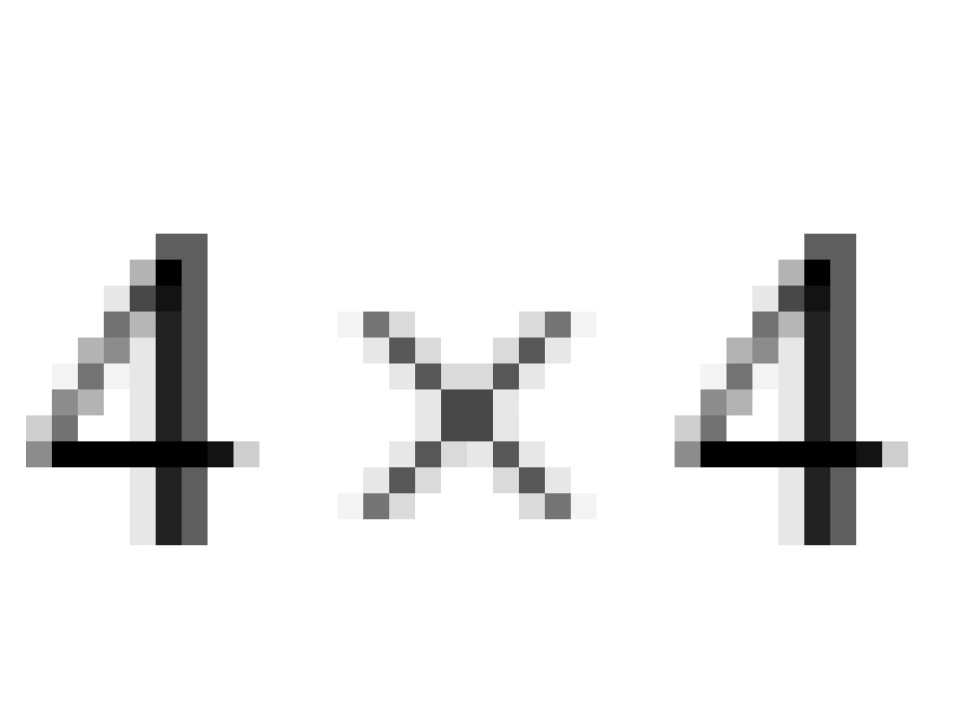
矩阵就被称为时空度规，但在这里被称为闵可夫斯基时空度规，它是主宰狭义相对论平直时空的。
第一个分量符号是正号，他代表时间分量，后面三个分量符号是负的，它代表三个空间维度。
在相对论中，时间和空间的区别就是依靠这种形式来区分的。
这种类似的度规被称为洛伦兹形度规。这种我们上面已经介绍过了，不懂的可以联系上面看一看。
好了，让我们回归时空弯曲这个话题。
引力是时空弯曲的表现的描述，是四维时空的弯曲。一般科普都用什么床单或者是蹦蹦床和大铁球来类比，其实这个不怎么好。因为这会让人误解为弯曲是向更高的维度弯曲。现实中这种完全是内蕴的。或者说实际上不需要这个额外维度（方向/自由度）就可以定义四维时空时空的弯曲。在广义相对论之中，用来描述时空弯曲的东西是黎曼曲率，这是一种内蕴性质，和时空本身的几何结构有关，不需要嵌入更高的维度之中。
但是对于三维以上的流形，它的不平坦或者弯曲，我们不知道到底怎么直观地表述，我们也画不出来，所以就只能通过外嵌的方法，将其嵌入到三维空间中，用二维弯曲来表示。但是它本身并不一定需要被嵌入。
通常我们只要得到了时空中每一个点的曲率就可以讨论时空弯曲。 那我再来讲一下什么叫内蕴，这是数学上的，但是我可以大概说一下。我们举个例子，有一个球，还有一个圆柱，他们俩都是弯曲的，有曲率，但是，一个内蕴可以独立于三维空间，一个是要嵌入三维空间中。 现在我们要做的就是，在不拉长和压缩它们表面的情况下，看看能不能通过某一种操作，让他们变成一个平面。结果我们发现球面是不可以的，但是，那个圆柱面可以被我们展开成一个平面。同样地，曲线和和圆柱面类似，也能被我们拉成直线。当然，上述例子有点的粗俗，但是，应该很容易懂吧。 所以说GR（General Relativity广义相对论）里，根本不用考虑，四维时空朝哪个方向弯曲。事实上，如果你看到类似的科普还会想到问这个问题的时候，就说明你认为还存在着五维空间以上的空间。 那么，通常在GR里，我们怎样知道弯曲呢？可以定义矢量平移。大致就是这样的:在时空某点P有一个矢量，我们沿着一小段闭合路径将其平移到其它点再返回原初点。如果发现与出发前的角度方向不一样，则表明时空在这一点存在曲率或者曲率不为0。如果模长不一样，那么说明不仅存在曲率，还存在挠率，关于挠率这个几何量，这里就不多说了。
在小区域范围内，这一点的曲率正比于平移矢量沿着闭合路径平移的路径所围绕的封闭的面积 和矢量发生变化的角度 。大的区域内就可以用积分把它们积起来。
因此，我们可以清楚知道，我们所谓的穿越虫洞，其实并不是走中间那条洞，而是沿着洞壁走的。
当然在我们看来，这个洞壁其实是三维的，洞口结构其实是球形的。
不过很可惜的是，爱因斯坦-罗森桥是不可穿越的洛伦兹虫洞，因为它能通过的仅仅是类空曲线，它不允许类时曲线和类光曲线穿过。
所以正常我们宇宙中的物体是不可能穿过的，包括光也不可以，只有超光速的东西才可以穿过，因为超光速的物体的时空曲线是类空的。
那么有没有可穿越的洛伦兹虫洞呢？
当然是有的。
对于这块研究要感谢索恩和他的徒弟莫里斯，他们对于球对称性洛伦兹虫洞的研究，开启了虫洞物理学的研究。我们下次再来讲讲他们的故事。
【本文为耀星会的原创作品，未经允许，禁止盗用、转载、篡改文章，否则耀星会和作者将追究版权责任。】
