科普驿站 第三十九期
主题：时光机与任意门（第一期）
科目：物理/宇宙
难度：B2
时间：2020.1.18
讲师：弦轴子
爱因斯坦求和约定
爱因斯坦求和约定：重复指标代表求和，此时求和符号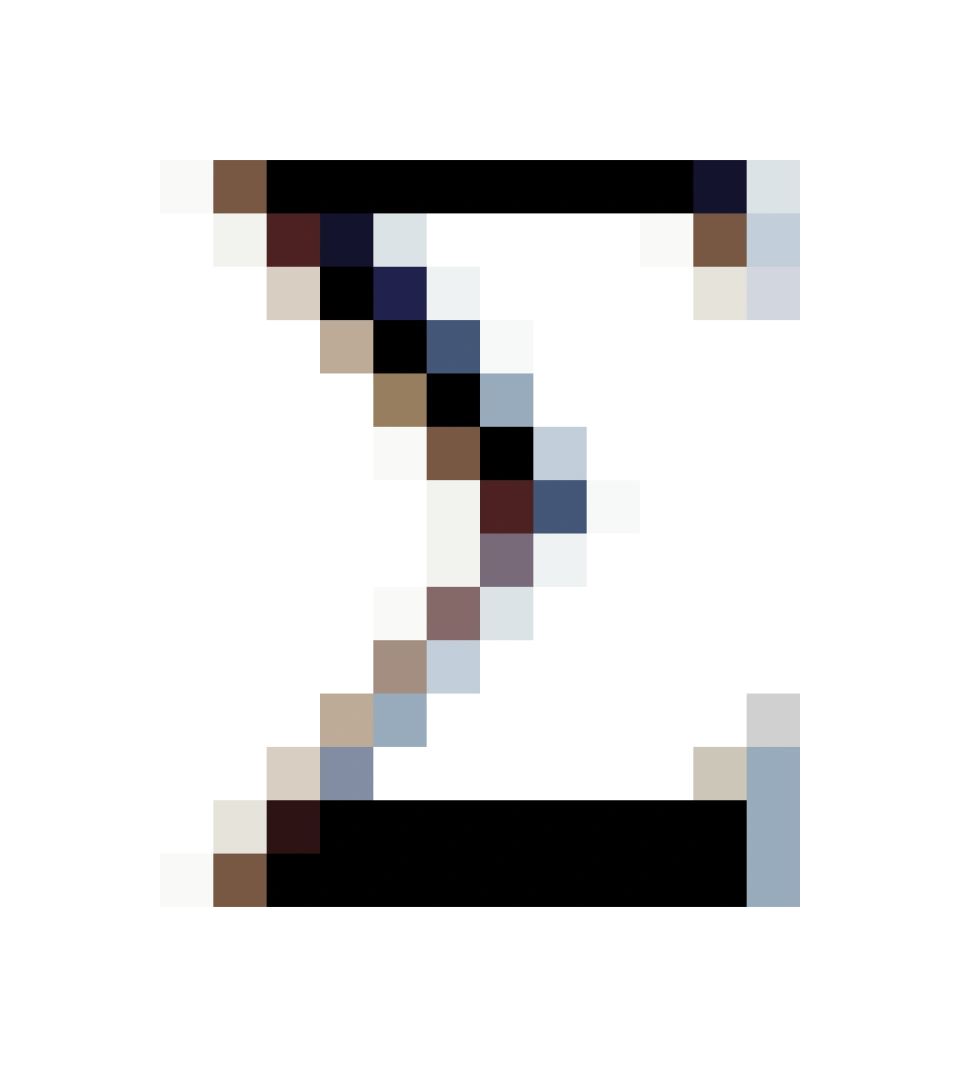
可以省略不写。
条件：1.重复是指求和指标在同一个指标中出现两次（有且仅有）。
2.求和指标在同一个表达式下必须一上一下。
例如：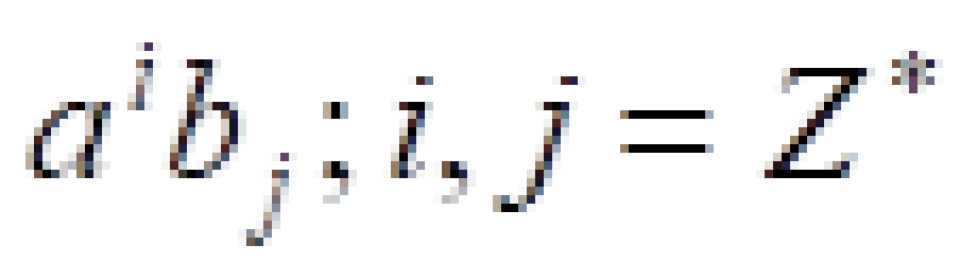
，i,j叫做求和指标，也可以叫做傀儡指标（简称“傀标”），而且可以看出在这个表达式下傀标是一上一下一一对应式分布的。傀标字母没有实际意义，只代表求和；因此，傀标字母是可以任意换取，只要满足上面讲的爱因斯坦求和约定的条件。
现在我们用爱因斯坦求和约定来改写上面度规求和。
条件1：重复是指求和指标在同一个指标中出现两次（有且仅有）。
在上式中,i,j出现两次（有且仅有）,因此，i,j是求和指标也叫做傀标。
条件2求和指标在同一个表达式下必须一上一下。
在上式中,傀标i,j在同一个表达式下是一上一下的。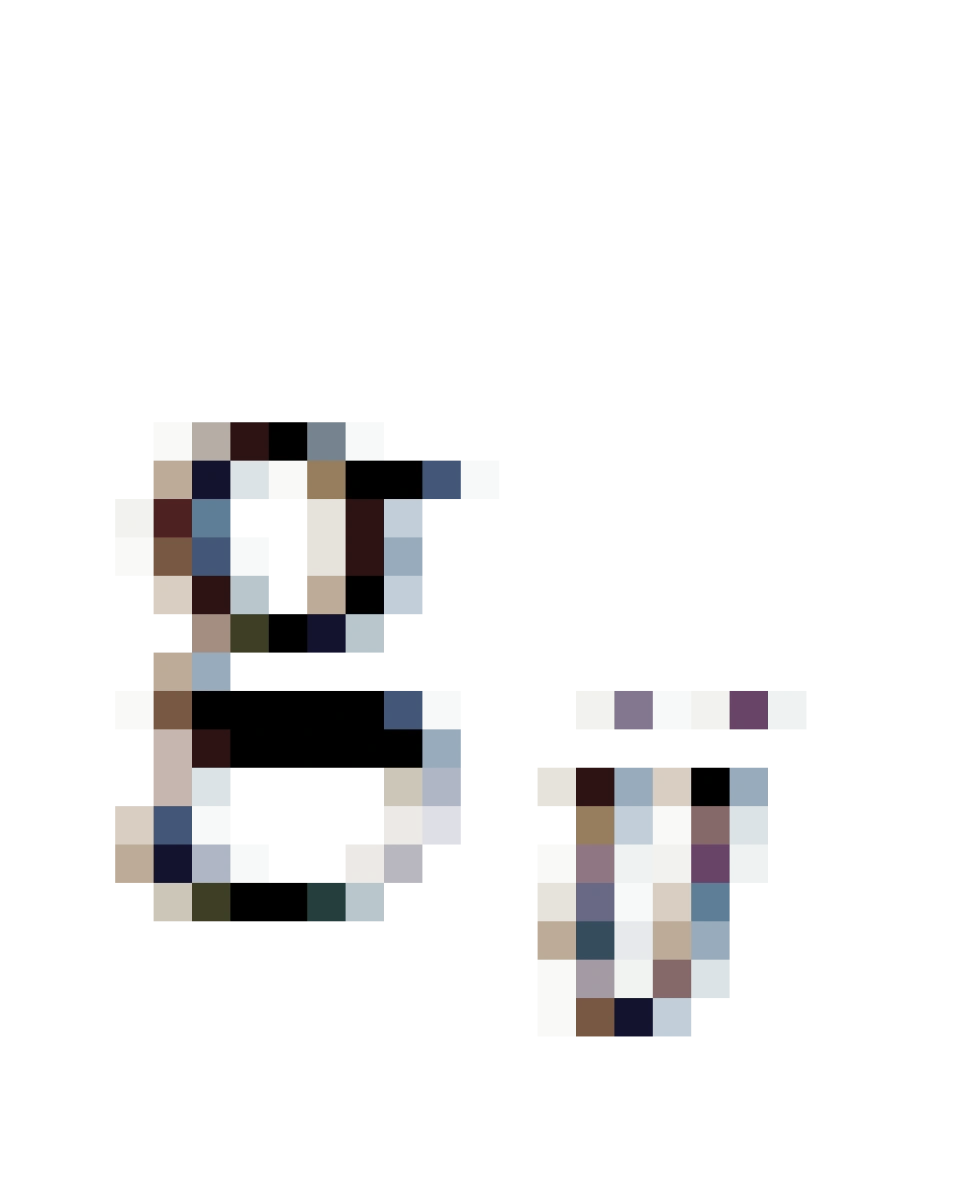 
中的i与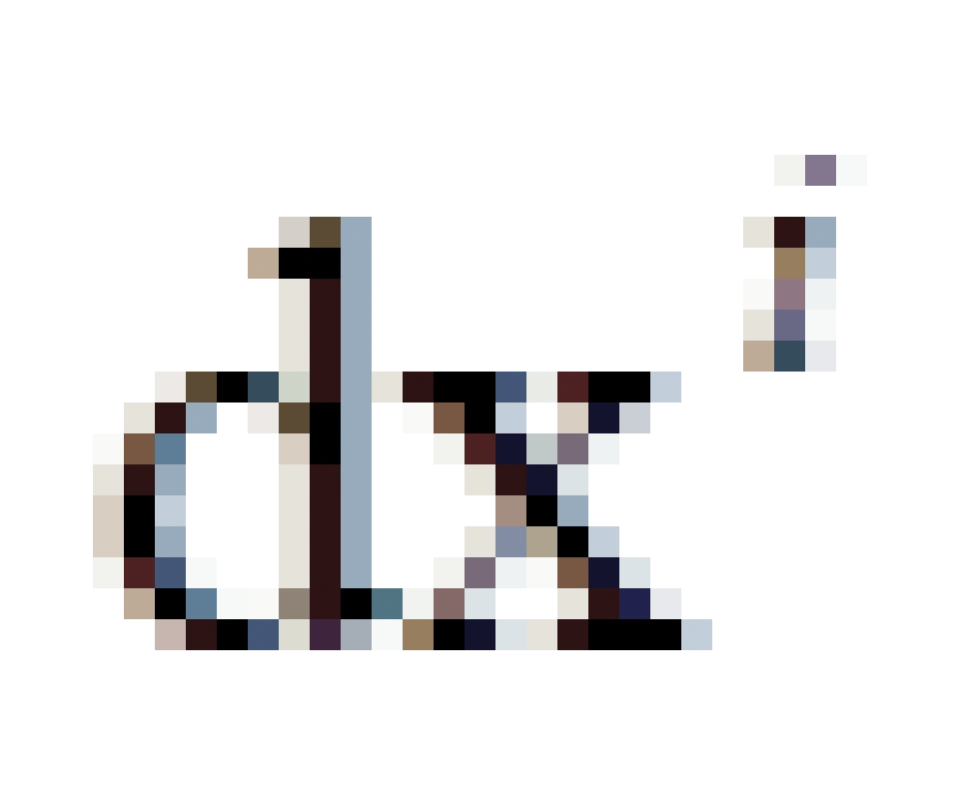
中的i是一上一下，一一对应式分布的, 
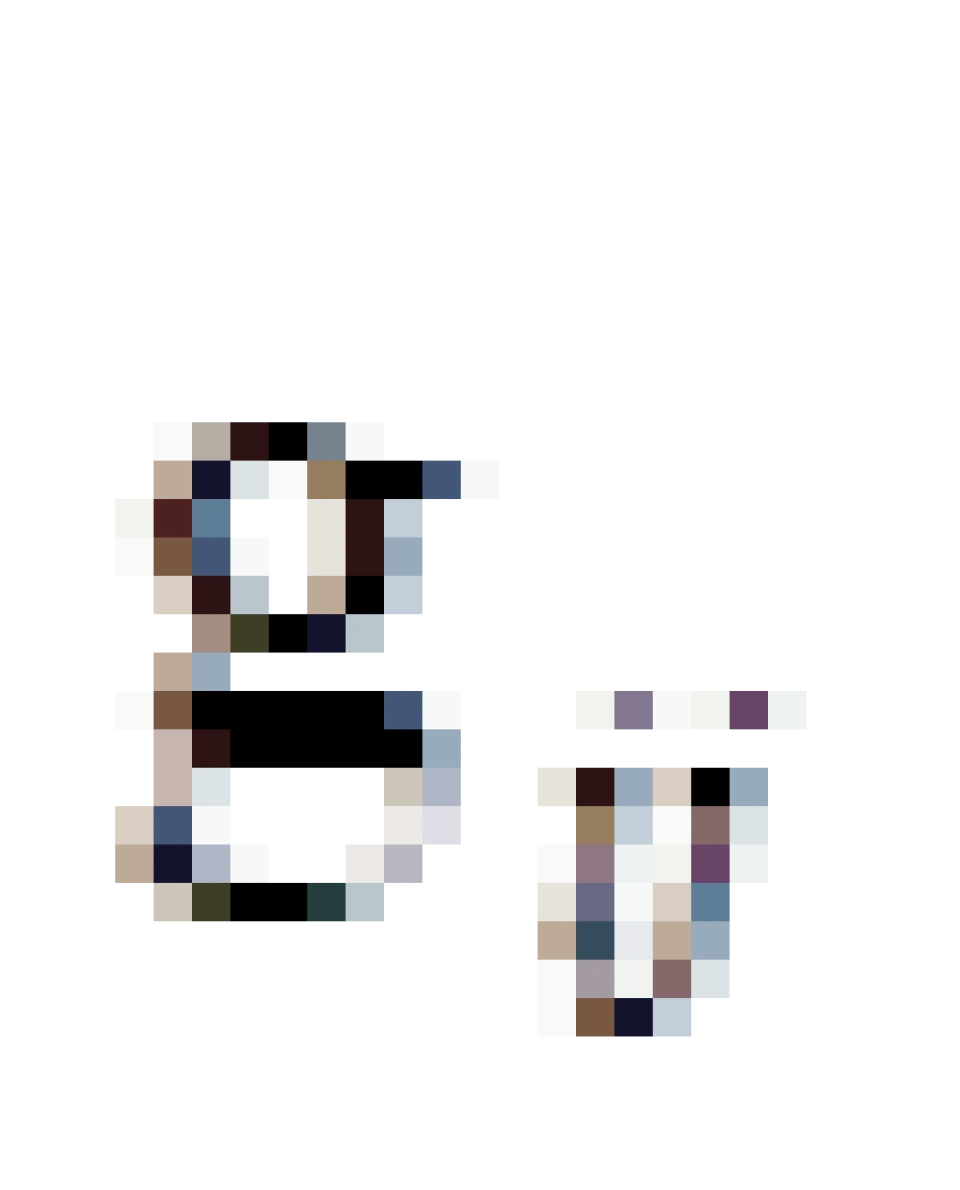中的j与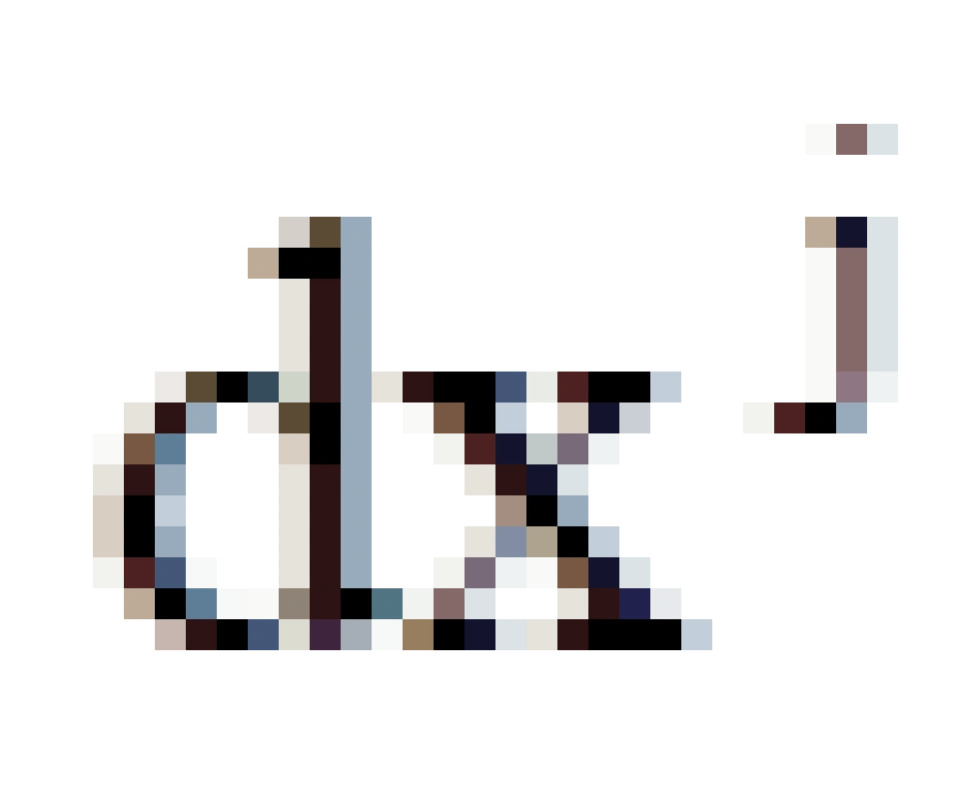 
中的j是一上一下，一一对应式分布的。
介绍完上面这些，我们就可以换一个记法来重新书写我们找到的任意两个惯性系之间的不变量。
这是我们找到的任意两个惯性系之间的不变量。现在我们换一个记法来重新书写一下。
被称之为闵可夫斯基时空度规。在相对论中定义时间和空间四维矢量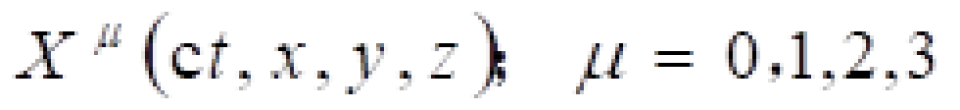
固有时间：对对于弯曲时空中的任意坐标系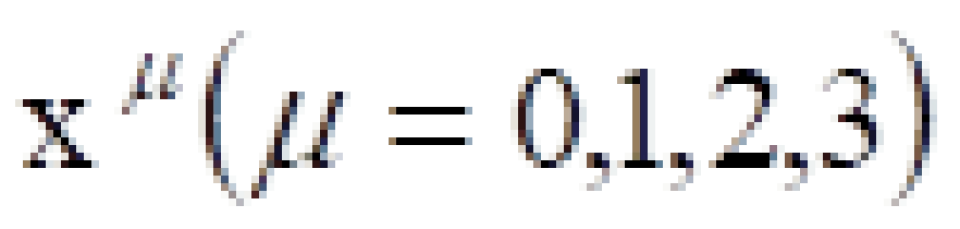
，如果视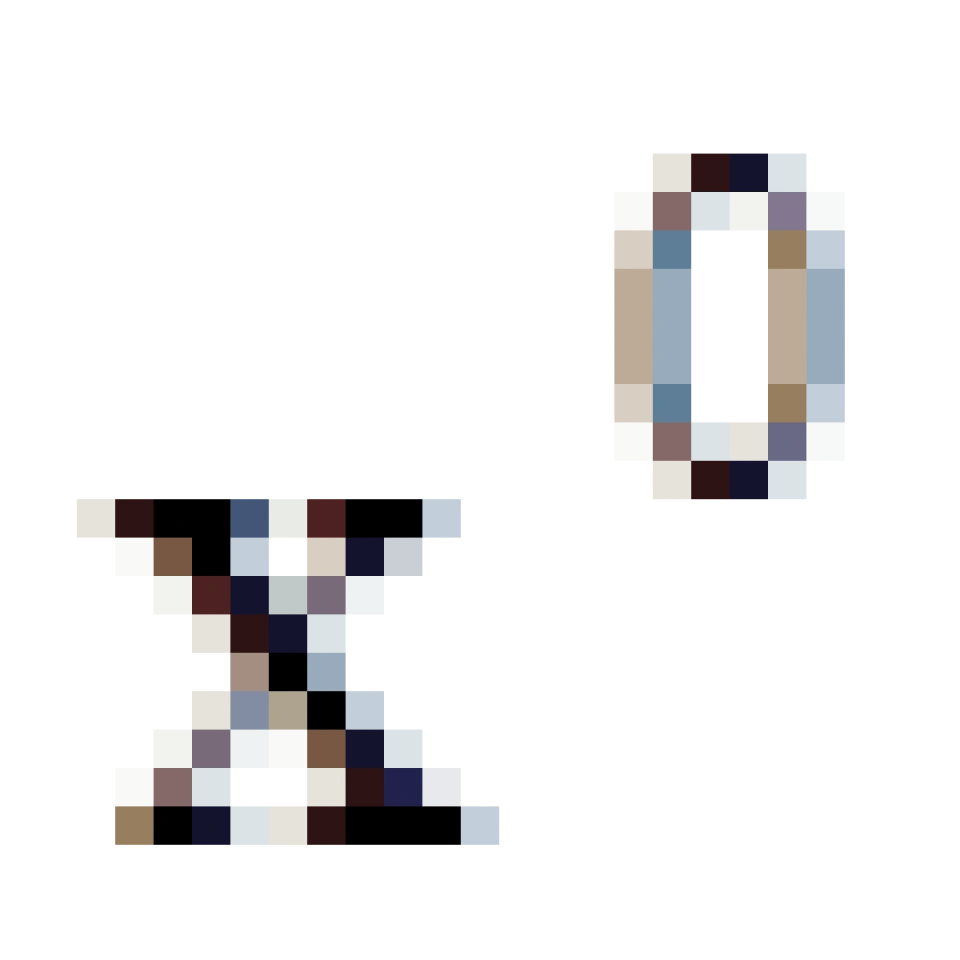 
为时间坐标，则以速率
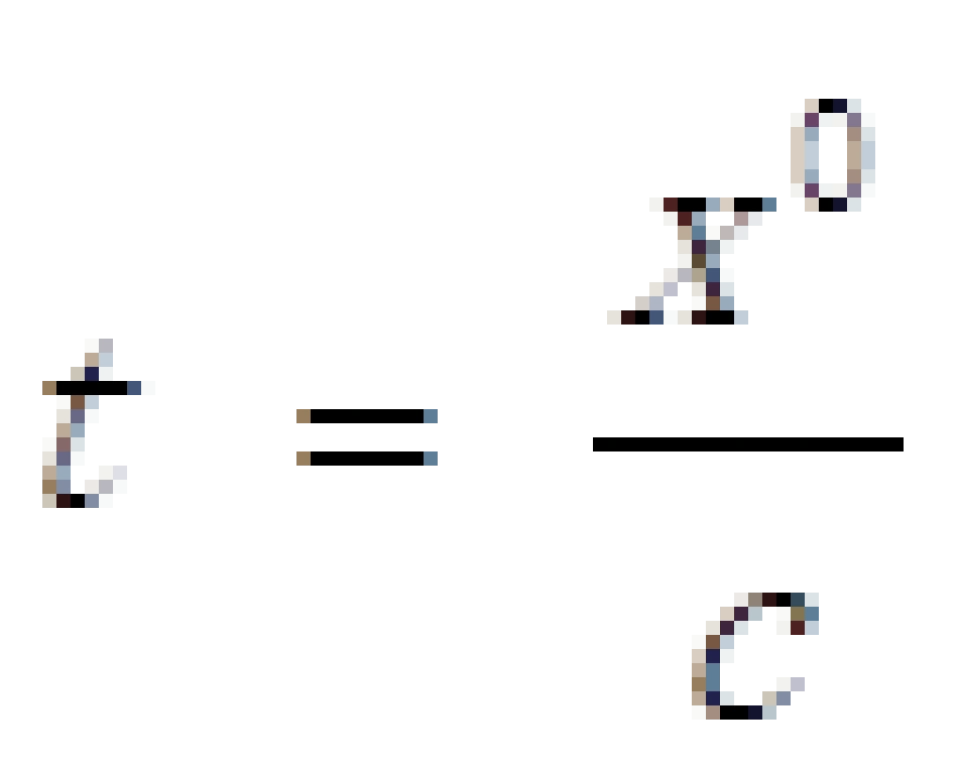运行的钟叫做坐标钟，t称之为坐标时间，c为真空中的光速。
在狭义相对论中，我们称固定于一个惯性参考系中的真实的钟为标准钟，它所记录的时间为那个惯性参考系的固有时间；亦即：静止于那个惯性参考系中的观察者亲身经历的时间。
按照这个定义。再根据我们上面找到的两个惯性参考系之间的不变量：
我们可以知道：
不过这有一个虚数单位i很麻烦，但是我们可以改变一下闵可夫斯基时空度规，就可以避免这个虚数单位i。
两个惯性参考系之间的不变量：
我们可以知道：
由此可以定义这个惯性参考系的固有时间为：
物理上时空的定义
物理上，时空的定义是流形（把它当作局部很像欧式空间的抽象东西）附带度规。这些度规往往是在这流形上分布的，逐点定义，所以又被称之为度规场。因此，物理上，时空的定义是流形附带度规场/度规结构。不过度规也不是随便的度规，必须是洛伦兹型的。
那么什么叫做洛伦兹型度规呢？
在上面我们介绍了什么叫做度规，可以看出它的非对角元素都是零，而有些对角元素都是正的。我们把这种非对角元素为零，但是对角元素不全是正的，而是有正有负的度规称之为不定度规。
相对论中的度规必须是不定度规。不过，满足的条件还不够，还要要求不定度规必须是一负三正或者是三负一正，这种类型的就被称之为洛伦兹型度规。为什么是这种奇怪的东西呢？因为正好对应着三个空间维度和一个时间维度。我们的宇宙目前看来是四维的。一维时间和三维空间，时间是一个维度的，而空间是三个维度的。
我们在上面介绍的闵可夫斯基时空时空度规：
可以看出它有两种形式，即它的对角元素是一负三正或者是三负一正。
那凭什么说它是对应着三个空间维度和一个时间维度呢？
让我们继续分析闵可夫斯基时空。
可以看出这两种形式都是正确的，只是时空度规不同而已。这不是重点，重点是时空度规的主对角元素分别对应着时空间隔前面的系数。时空间隔一共有四个部分组成，分别是一个时间项与三个空间项。这些项前面的系数正好对应着时空度规的对角元素。因此，你就可以明白为什么说时空度规的对角元素是一负三正或者是三负一正是对应着三个空间维度和一个时间维度。
不定度规是一负三正或者是三负一正，这种类型的被称之为洛伦兹型度规。四维流形（把它当作局部很像四维欧式空间的抽象东西）附带洛伦兹型度规在物理上就被称之为时空。
不过在相对论中，并不是只有闵可夫斯基时空时空度规而是有很多时空度规。只不过四维流形（把它当作局部很像四维欧式空间的抽象东西）附带闵可夫斯基时空时空度规（洛伦兹型度规的一种）被称之为闵可夫斯基时空。而有的是附带史瓦西时空时空度规（洛伦兹型度规的一种）则被称之为史瓦西时空。
大概基础介绍到这里。另外，为了方便讨论，我们今后选用自然单位制 ,并且如无特殊说明，时空度规选取是一负三正。
（事实上时空度规并不是只有一负三正或者是三负一正，只要保证有三个正的一个负的就可以，至于怎么搭配哪些对角元素都是任意的。）
现在基础基本上铺设完了，我们开始讲一讲第一个可以充当时间机器的模型——虫洞。
虫洞
幸运的是物理上，虫洞这个东西可以被改造成时间机器。
虫洞是广义相对论预言出的一种特殊的天体。
它是爱因斯坦引力场方程的一个解，用来描述连接两个渐近平直时空的 “桥梁”，换句话说就是连接两个平坦时空区域的“桥梁”。
关于这个虫洞的解释最早可以追溯到1935年，在爱因斯坦与以色列物理学家 Nathan Rosen合作发表的一篇题为 《广义相对论中的粒子问题》的论文中被提到。
而关于“虫洞”这个术语，则可以追溯到1957年。Wheeler 与 Misner 师徒俩合作发表了一篇题为在《作为几何学的经典物理学》的论文。 Wheeler 与 Misner 在文章中这样说道: “拓扑学家们会把自己提出的结构称之为‘多连通空间’(multiply-connected space)， 但物理学家们也许可以将之更生动地称之为虫洞。”
后来这个术语被Wheeler的学生Thorne 所继承， 并经 Sagan 普及，逐渐被大家所沿用至今。
让我们回到1935年，爱因斯坦与以色列物理学家 Nathan Rosen合作发表了一篇题为 《广义相对论中的粒子问题》的论文。
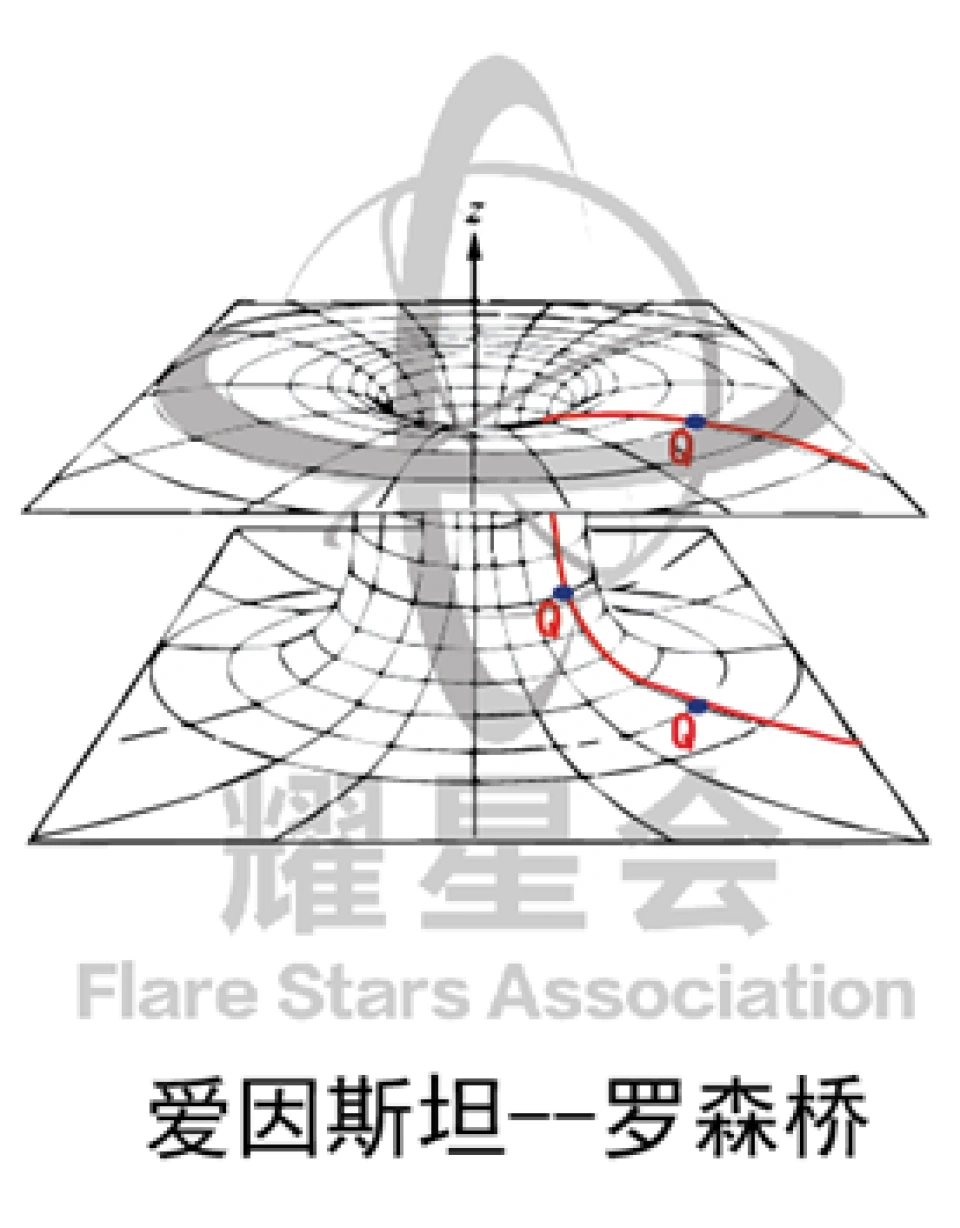
在这篇论文中他们提出了一种时空隧道被称为爱因斯坦一一罗森桥。
爱因斯坦一一罗森桥其实是不可穿越的洛伦兹虫洞。
我们来简单地看看最早的概念是怎么来的。
首先考虑最简单的史瓦西时空，
我们都知道，在广义相对论的框架中，物质的分布和运动影响时空结构，引力是时空结构的弯曲的几何表象。引力场的物理效果可通过黎曼几何中的几何量一一度规张量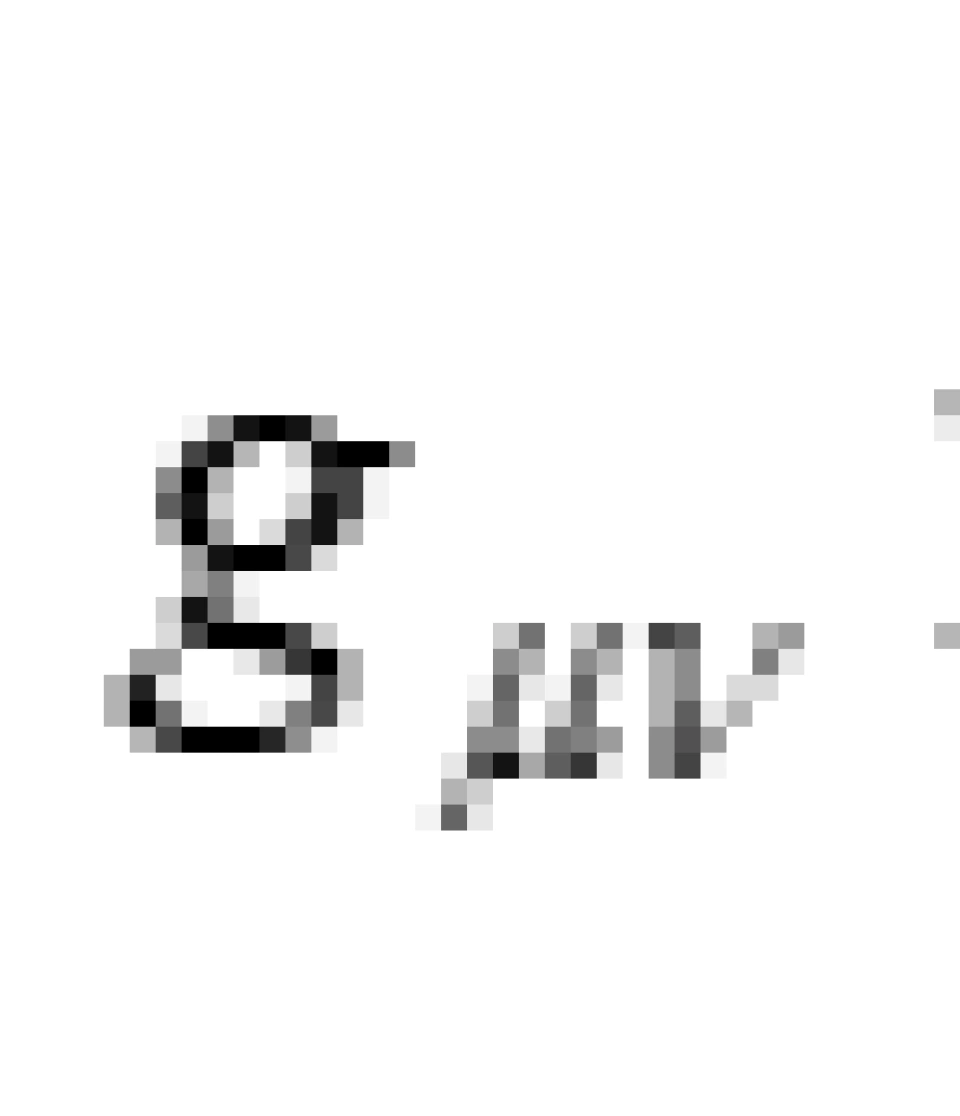
来体现。而物质的分布和运动如果用一个二阶张量来描述，那就是能量动量张量。它是一个4×4的矩阵，有16个分量，包含能量流，动量流，能量密度还有三维空间中各个方向的应力/压强。
因此，描述引力相互作用的爱因斯坦引力场场方程的一端是描述物质场运动和分布的能量动量张量，另一端是反映时空结构变化的张量，而且以度规张量为函数。具体推导过程就不说了，直接写出爱因斯坦场方程。
爱因斯坦引力场场方程其实就是：
曲率项=物质项
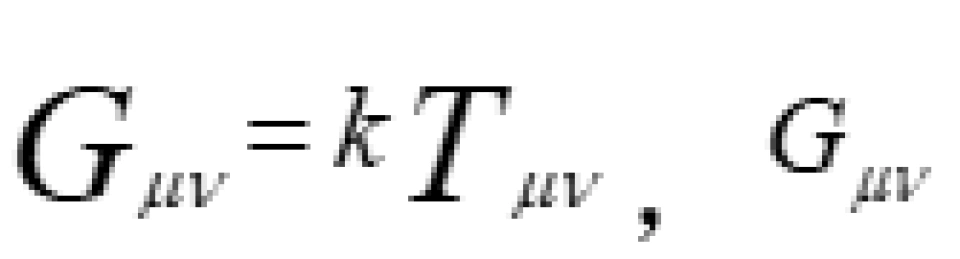被称为爱因斯坦张量（这里是不加宇宙项的）。其中：
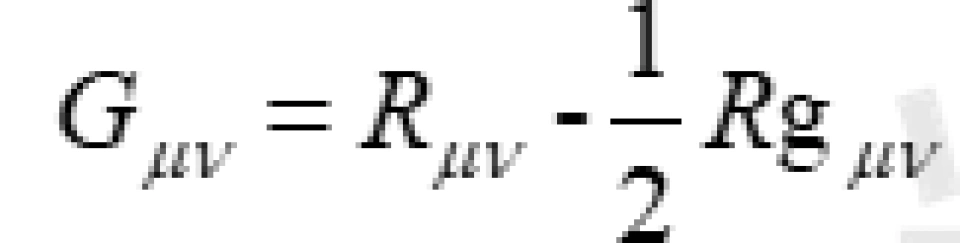，这里每个都是4×4矩阵，有16个分量，它们是对称张量，k为系数（
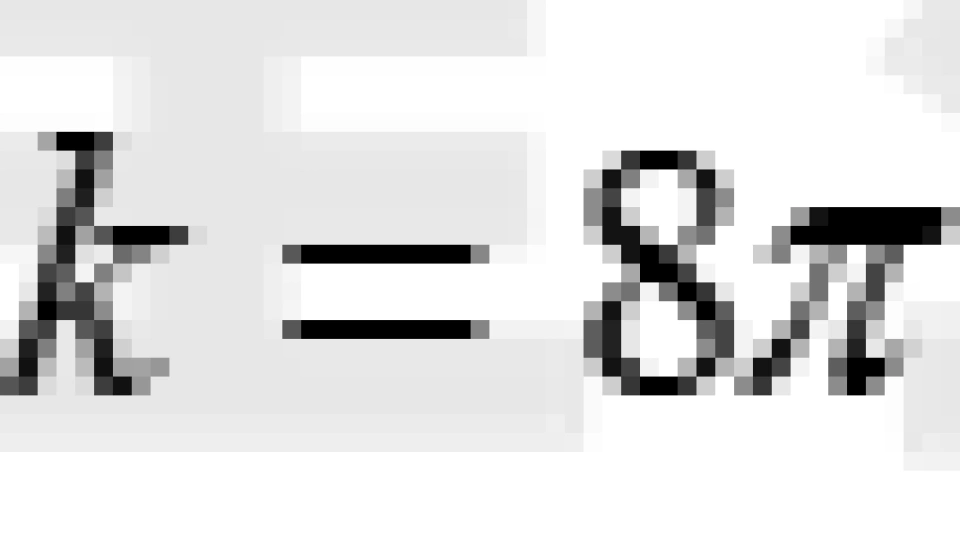，它的具体数值可以用场方程退化成牛顿引力方程的方法求出），
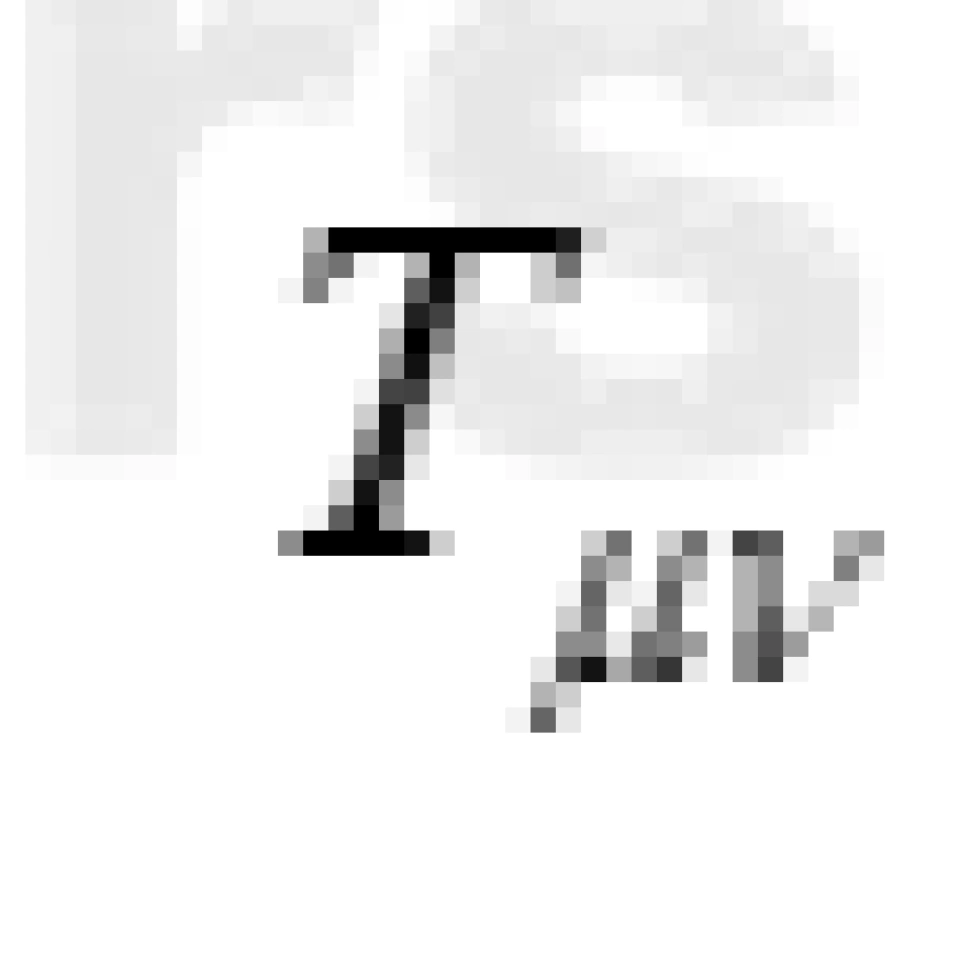是描述物质上的分布和运动的能量动量张量。
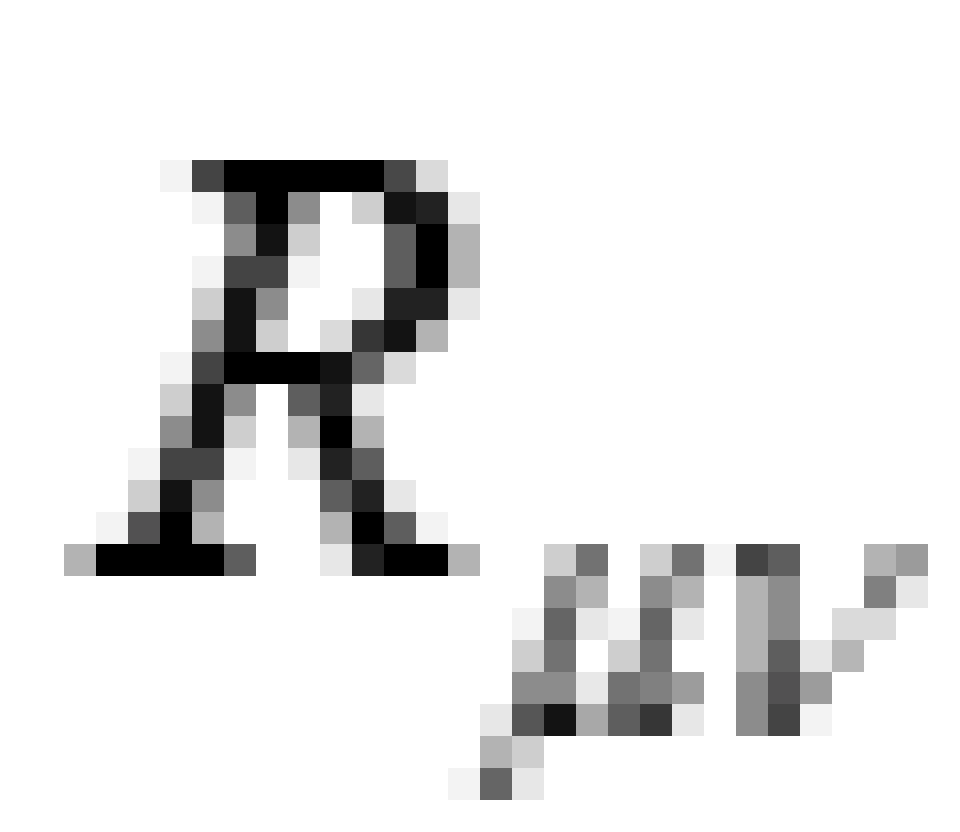被称为里奇张量，它是由四维黎曼曲率张量
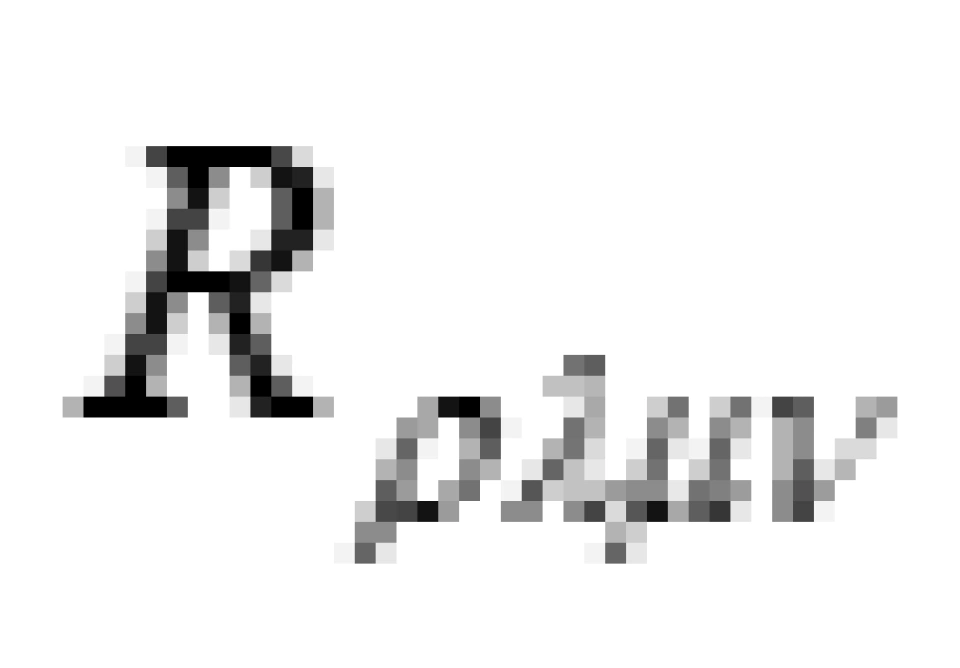缩并而来的亦即：
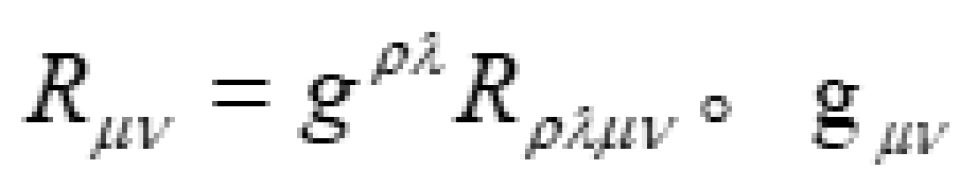就是我们前面说的度规张量，而R它叫做曲率标量，是由里奇张量缩并而来的亦即：
。
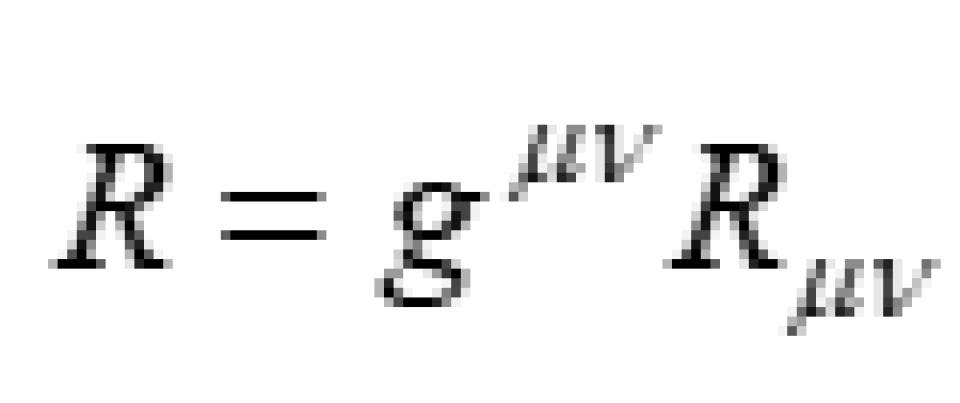你可以把张量缩并当做是一种矩阵求迹的扩展。一个二阶张量的分量用矩阵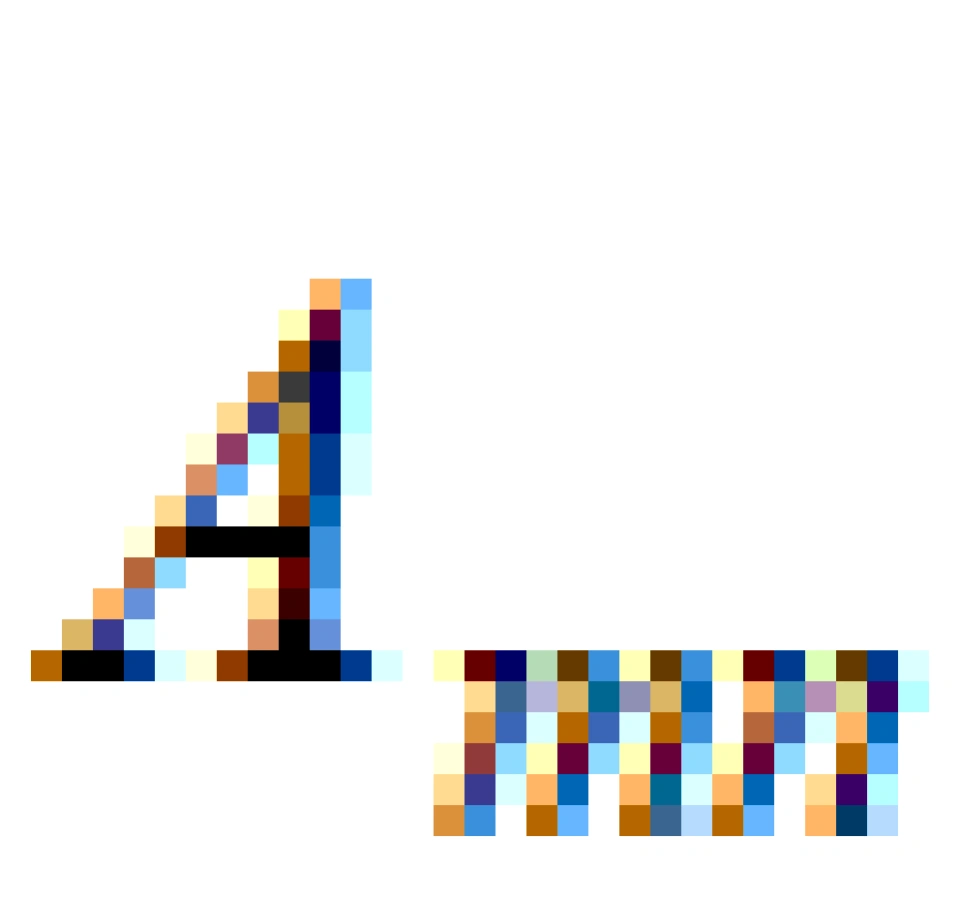
表示，当m=n时，只剩下对角线上元素，所有对角线上元素的和就是迹，亦即缩并为一个标量。迹，只在二阶张量也就是矩阵上有定义，它在高阶张量上的推广就是张量的缩并。
其实也不难理解，因为张量本身就是矩阵的高阶扩展。三阶张量缩并就是一个矢量，缩并后降两阶。
引力场的分布在广义相对论框架中，其实就是与度规场的分布有关。度规场其实是关于度规的一套分布函数，该函数是由爱因斯坦场方程来确定的，由爱因斯坦场方程能直接求出度规的分布函数，但是不能直接求出某时空点的度规。所以首先是由场方程求出对应的度规场函数，然后才能得到某点的度规。
当然有的时候爱因斯坦场方程很难求解（外界条件不是球对称时 很难求出精确解），因为广义相对论场方程也就是爱因斯坦引力场场方程是由10个二阶非线性偏微分方程构成的方程组，应以确定10个决定时空几何性质的未知函数，也就是度规张量的10个独立分量。度规张量是4×4矩阵，一共有16个分量，但是由于度规张量是对称性的，所以最后只有10个独立分量。它们对应着10个二阶非线性偏微分方程。这个方程组内还有4个恒等式，因此真正有用的独立方程只有6个。不过要想解方程，还必须引入4个跟坐标系选择有关系的微分方程，被称为坐标条件。这样加起来，独立方程还是10个。十个方程，十个未知函数，10个独立分量正好匹配。不过，如果想真正解微分方程，还必须有初始条件和边界条件。由此可见，实际上去求解爱因斯坦引力场场方程是一件很困难的事情。
解爱因斯坦场方程其实就是在求解度规场的分布函数。
我们下期继续介绍。
【本文为耀星会的原创作品，未经允许，禁止盗用、转载、篡改文章，否则耀星会和作者将追究版权责任。】
更多科普资源和答疑，请加入耀星会科普官方QQ群：433646418
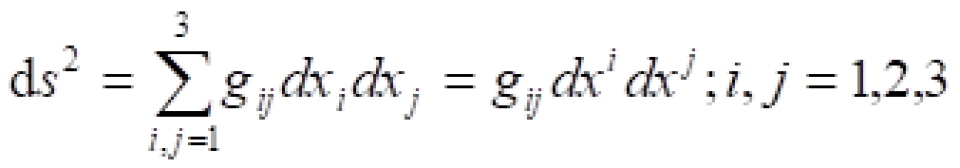
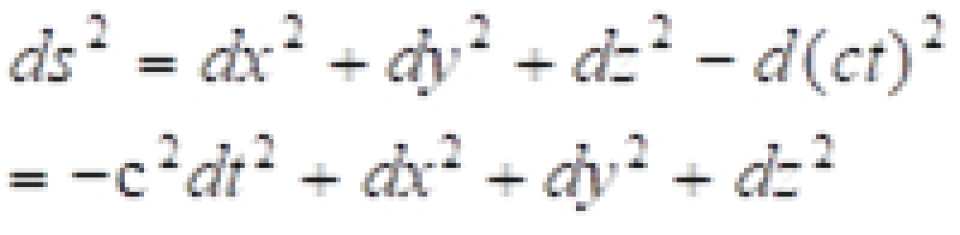
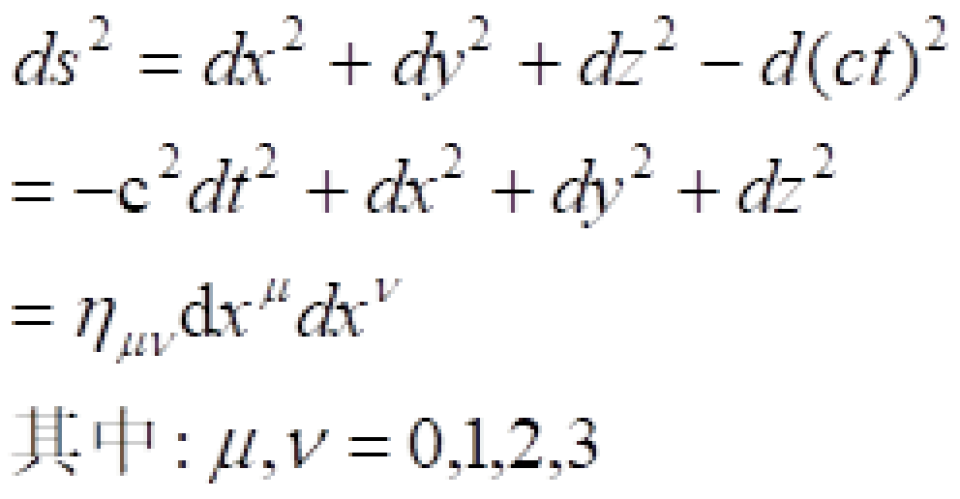
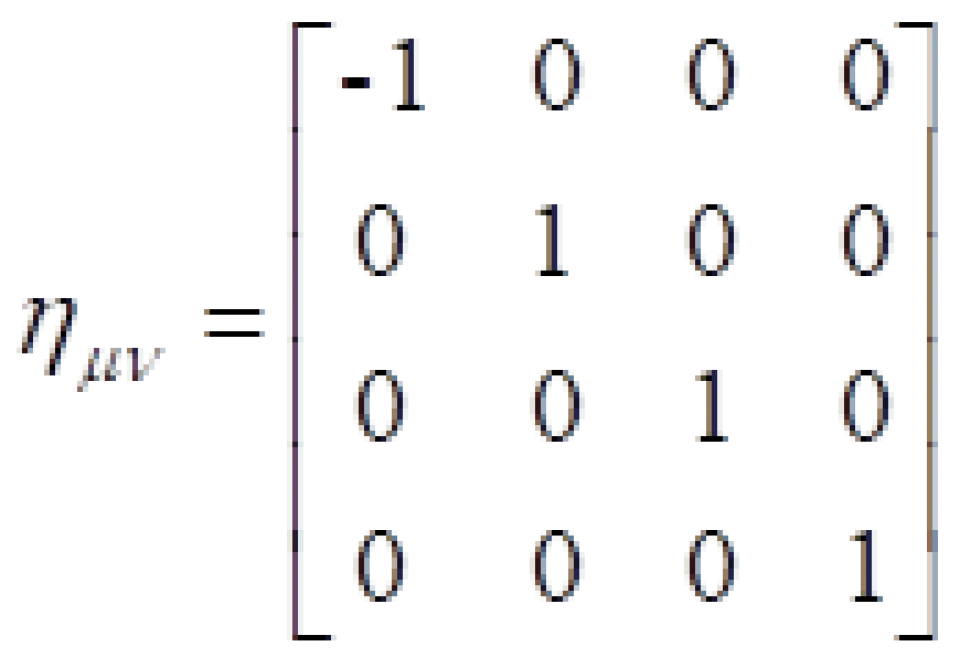
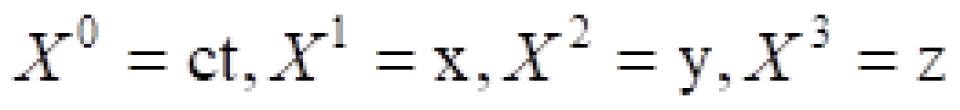
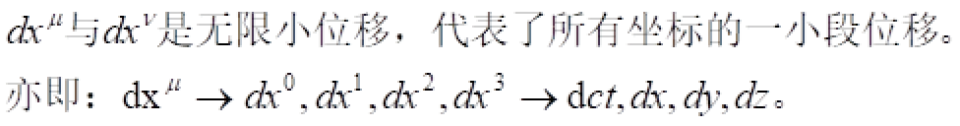
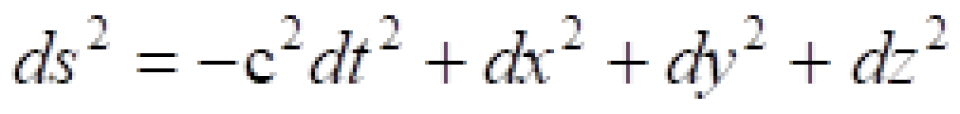
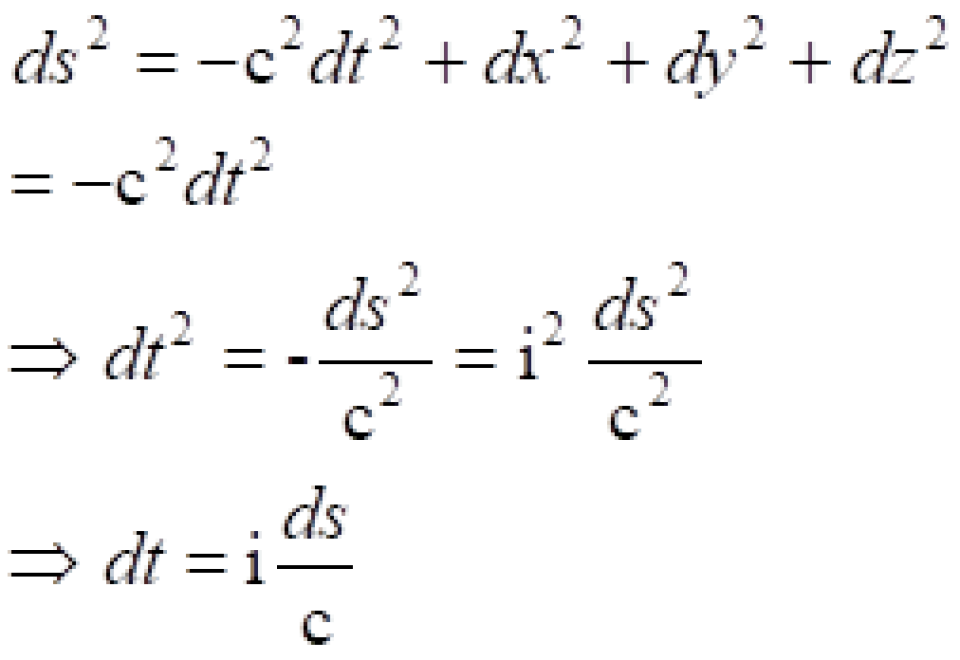
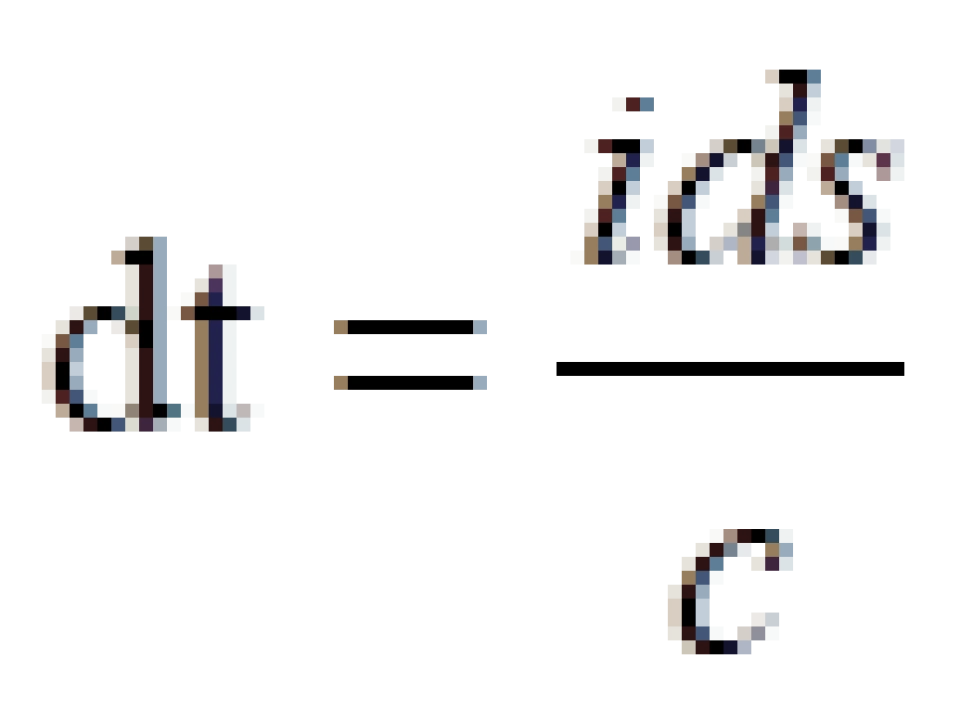
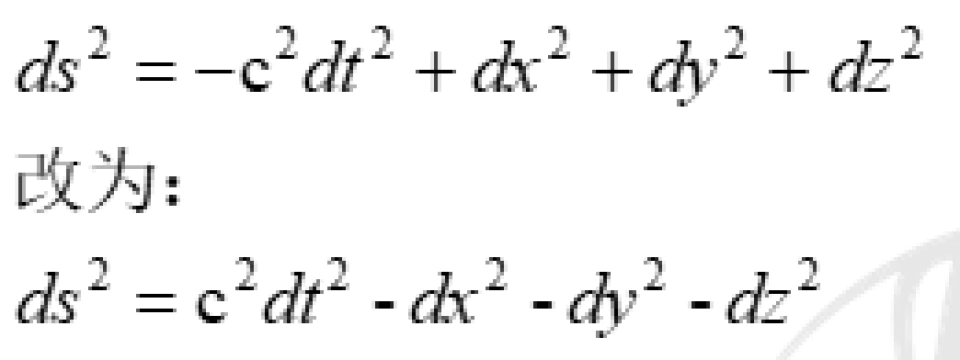
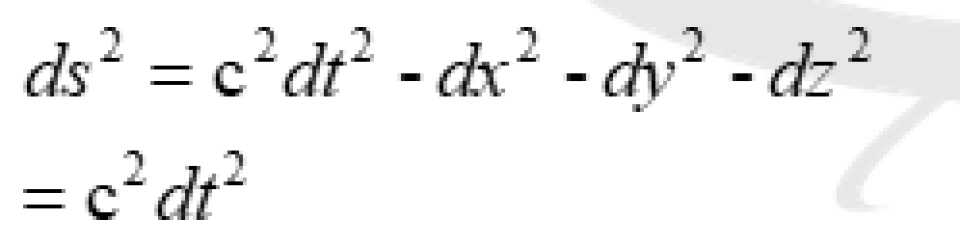
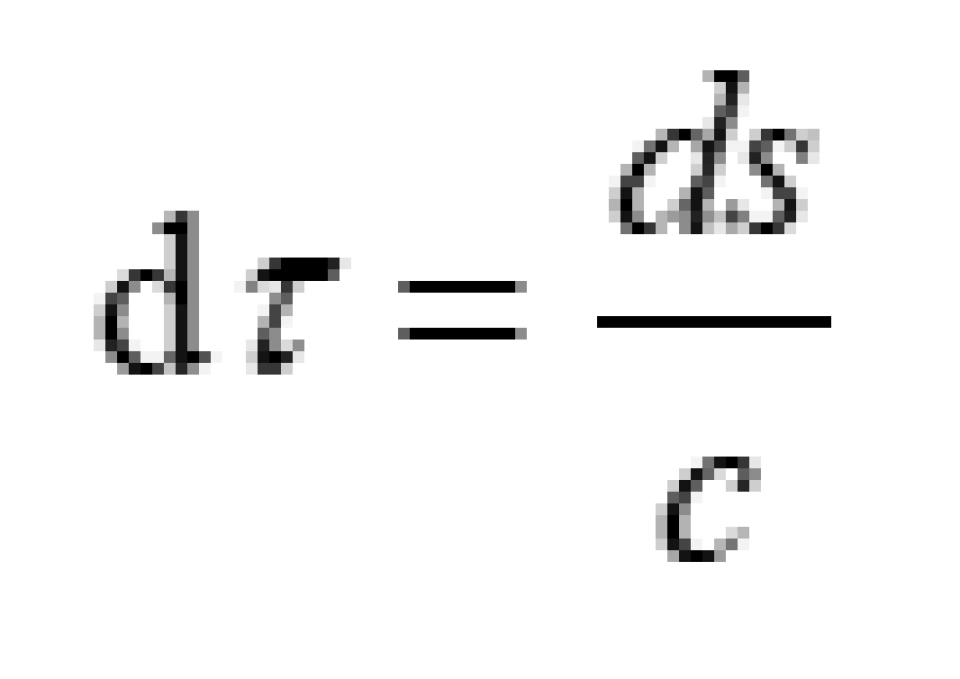
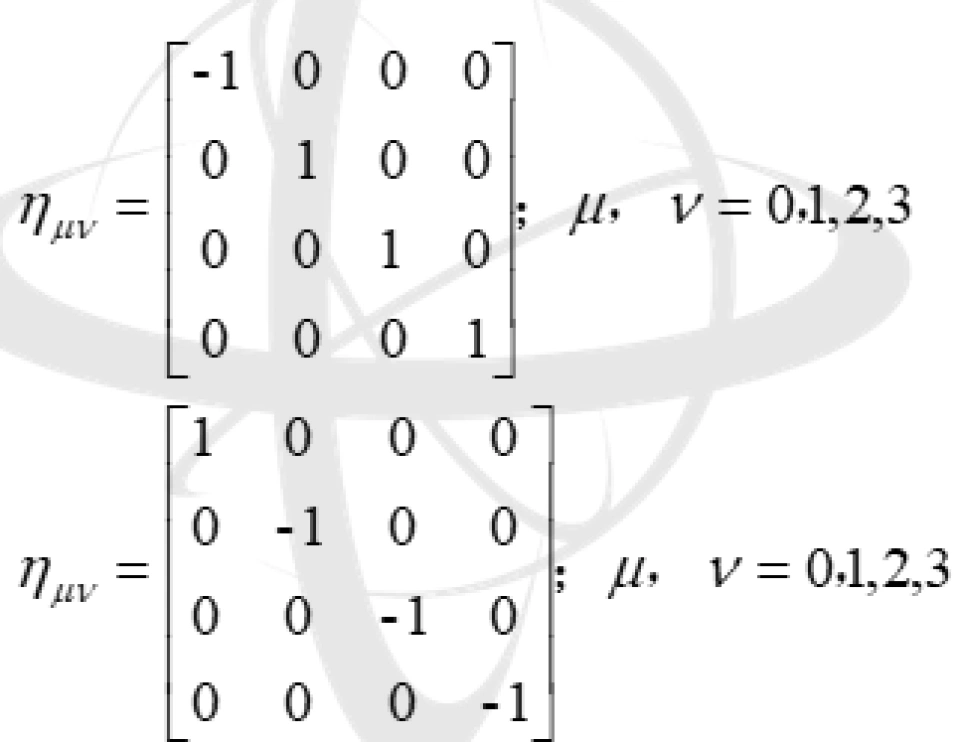
奖励金币：+10
奖励理由：内容丰富饱满