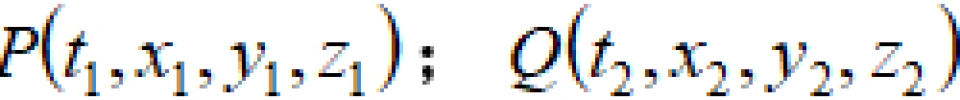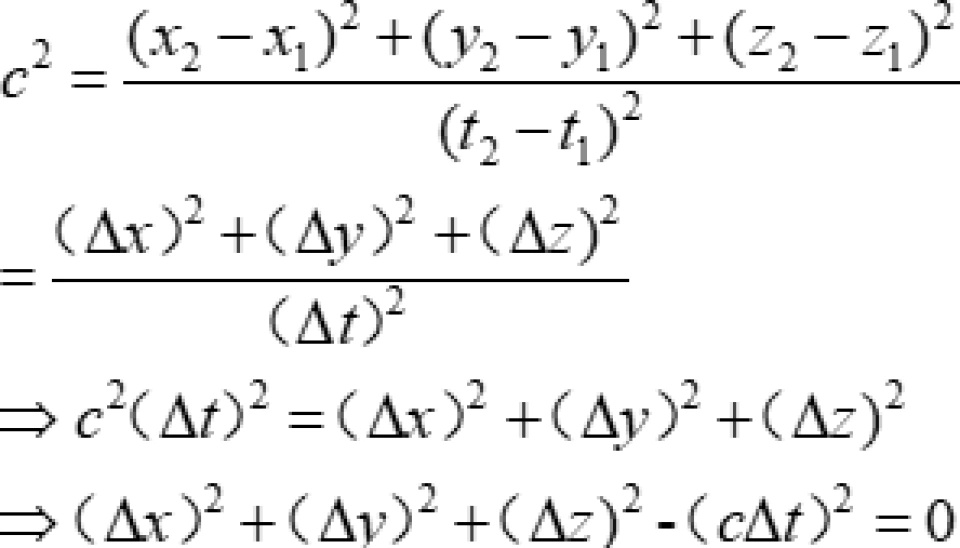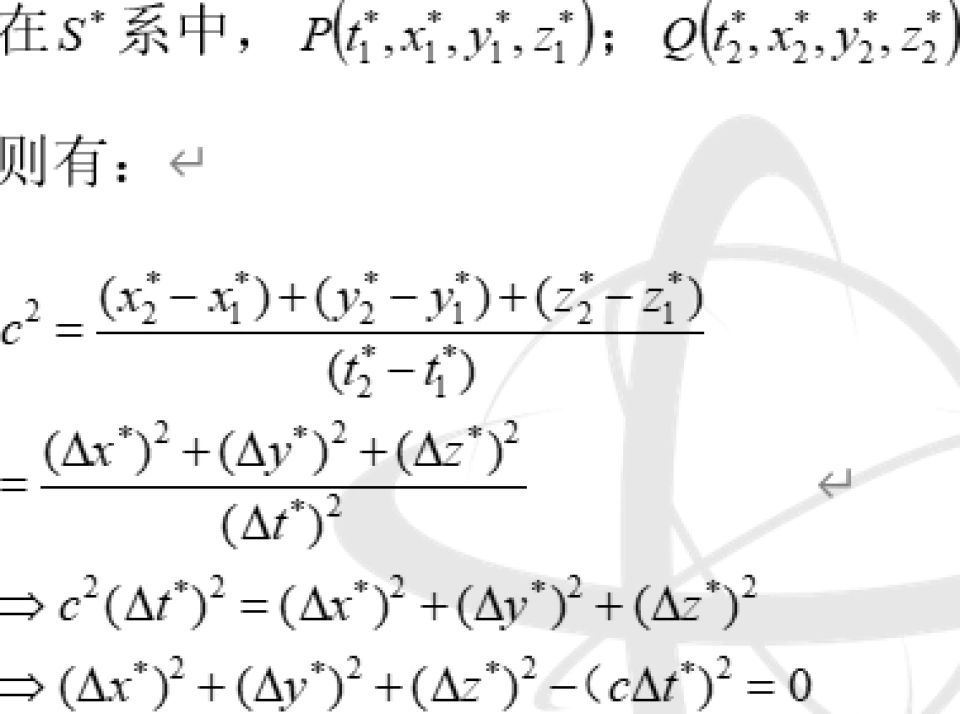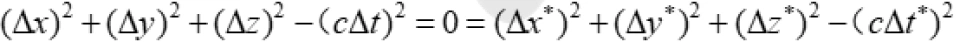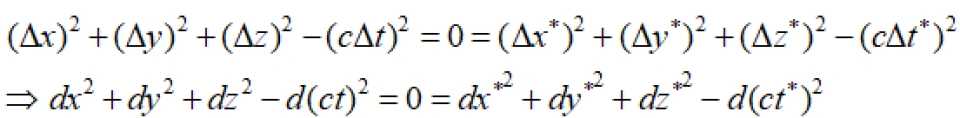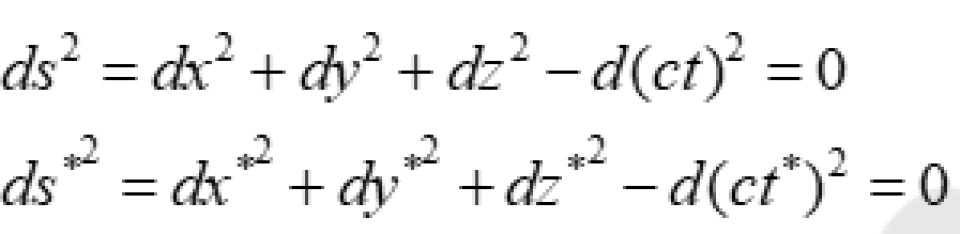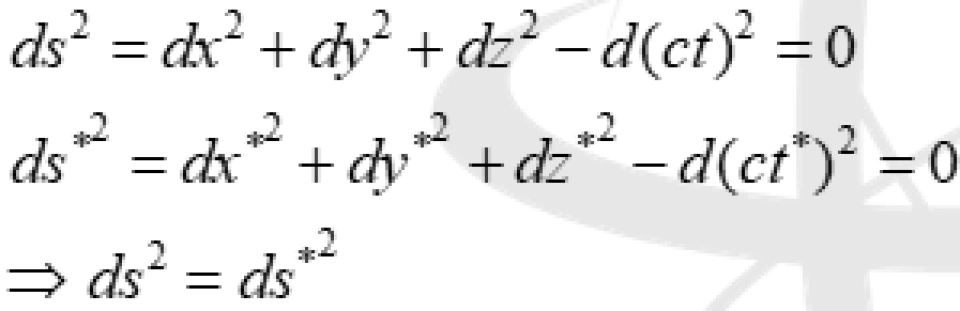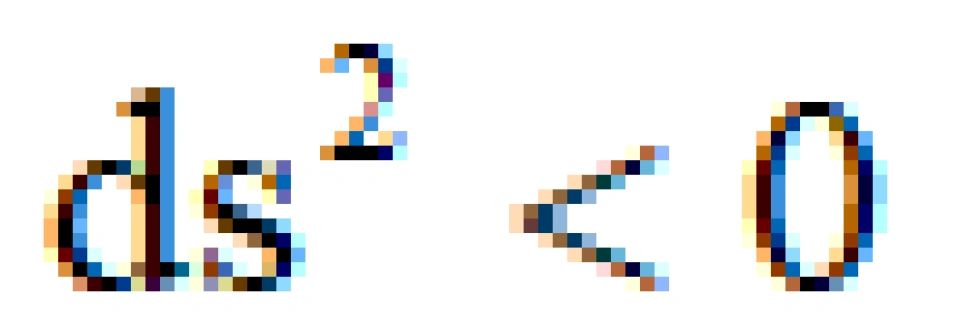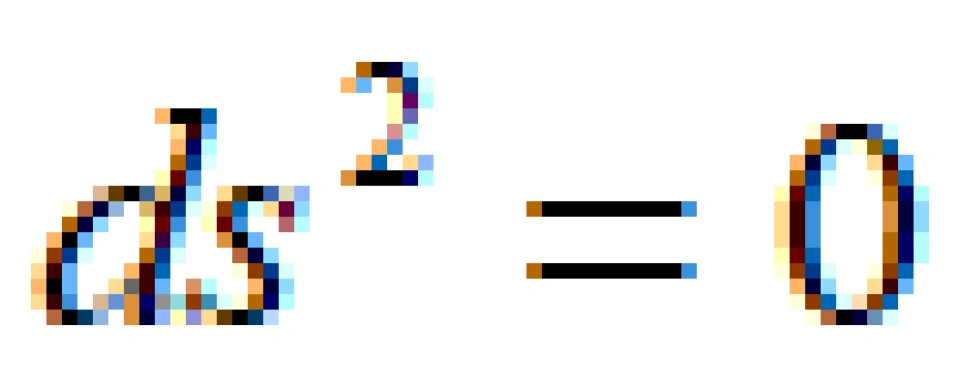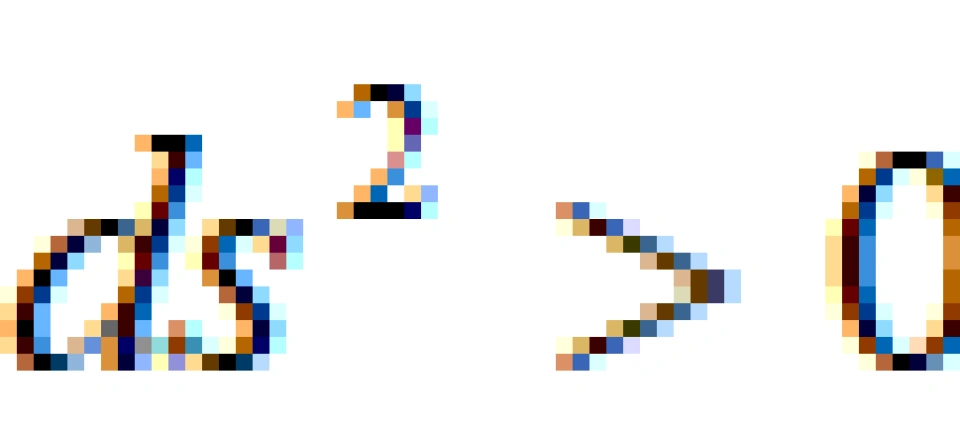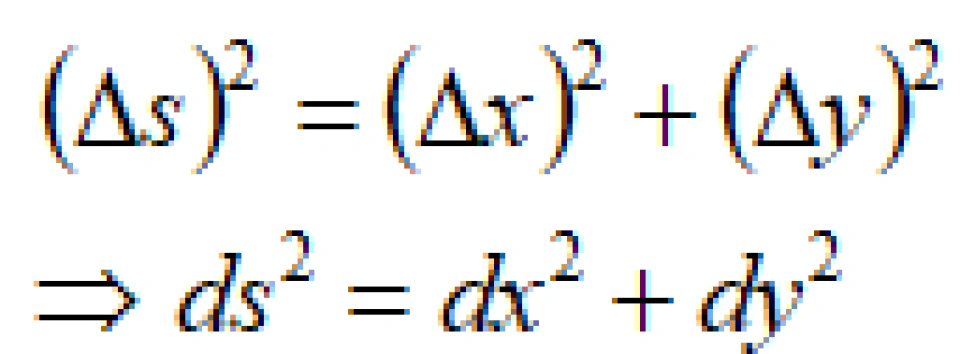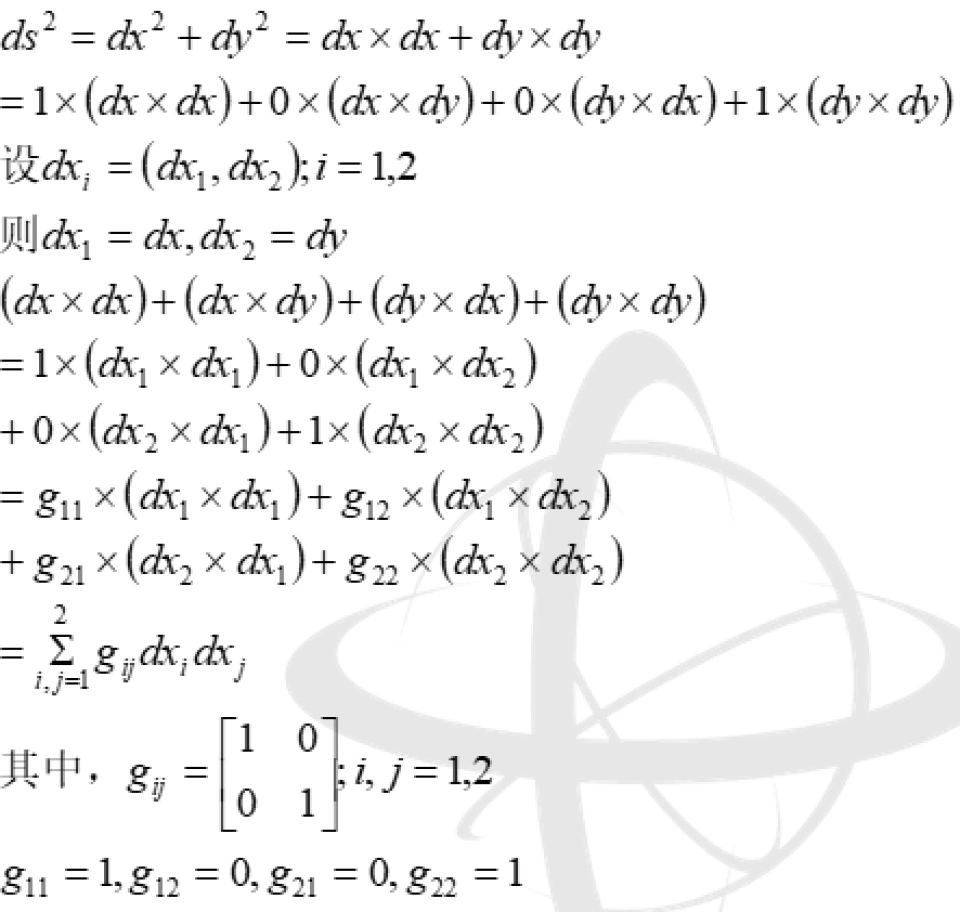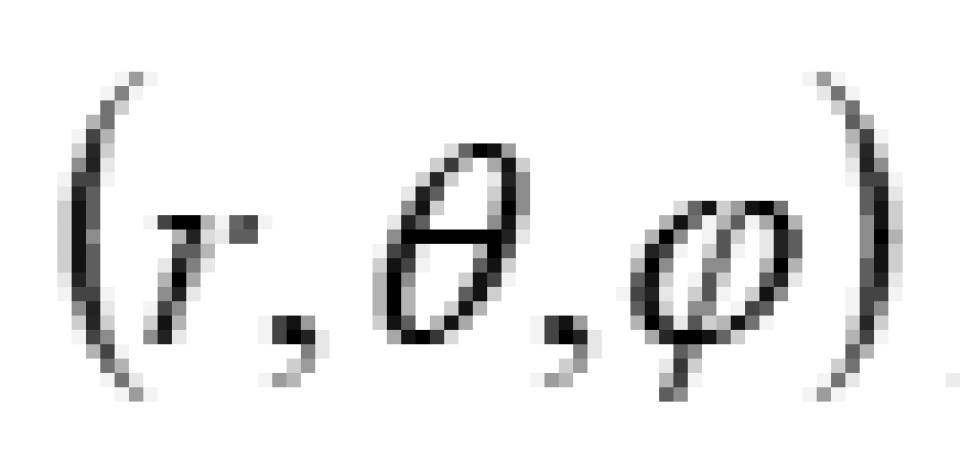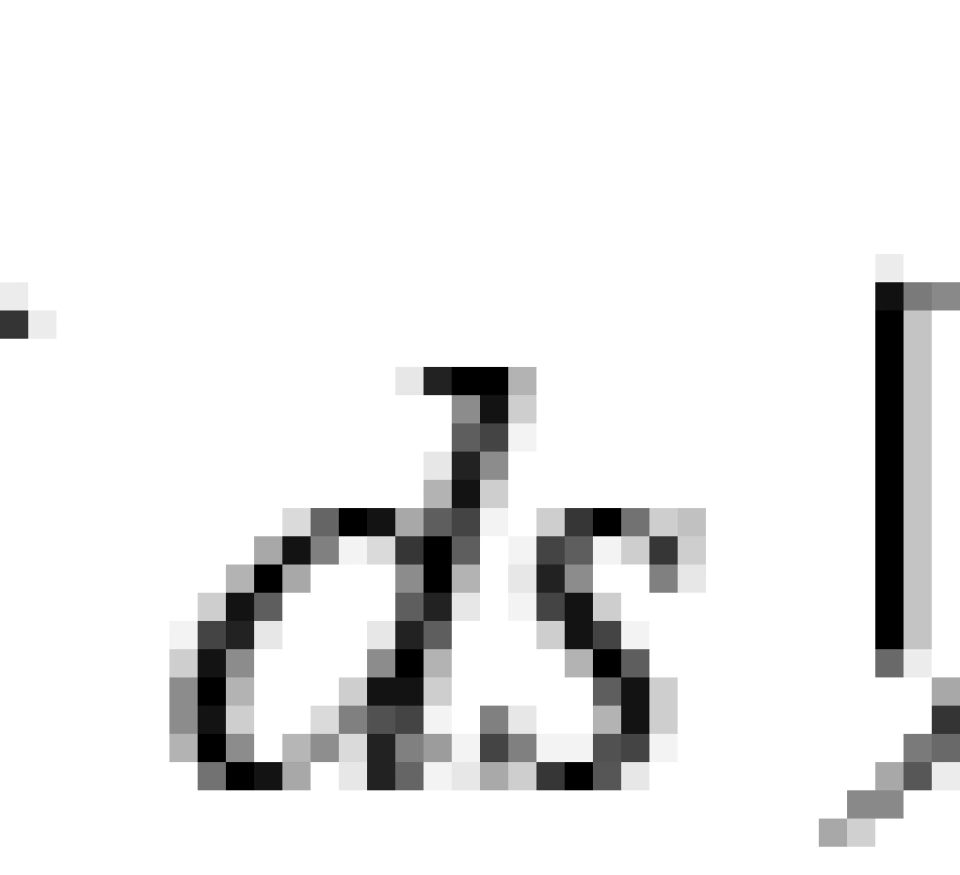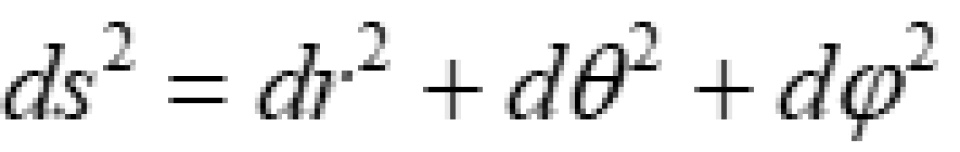科普驿站 第三十九期
主题：时光机与任意门（第一期）
难度：B2
讲师：弦轴子
“遇事不决，量子力学。解释不通，穿越时空。篇幅不够，平行宇宙。”作为在整个科幻界都流行的梗，并不是空穴来风。解释这个梗，就是本期科普驿站的主要内容。
大雄的孙子通过时间机器把哆啦a梦送到过去给他的爷爷大雄。哆啦a梦有两个非常好玩的道具，一个就是任意门，另一个就是时空机。
任意门，只要给它坐标，他可以去世界上任何一个地方。时空机可以穿梭过去和未来。
虽然这是一个动漫，但现实中我们真的可以从理论上来制造出任意门和时空机？如果我们真的可以，那么将会带来哪些问题？
我们首先说一下时空机，能够穿越时间回到过去或者未来。这在科幻小说的中早已司空见惯。
比如，威尔斯写于1895年的《时间机器》中的时间机器，还是《回到未来》三部曲中的那辆汽车等等。
那么这些科幻设定幻想在理论上有没有相类似的东西呢？
答案是有的。
理论上有四种可以制造时间机器的理论模型：
第一种就是虫洞，
第二种就是一些宇宙学模型，这个些宇宙存在着闭合的世界线，宇宙中的物质会一遍一遍的走过之前经历的时间。
第三种就是提普勒圆柱体，这种就是利用高速旋转的圆柱体，周围时空会形成闭合的轨迹。
第四种就是利用由于由于早期宇宙逐渐冷却发生的对称破缺相变从而产生的线性结构一一宇宙弦，宇宙弦的快速旋转振动可以使周围时空闭合，物体的空间轨迹包括时间轨迹都是闭合的。
这四种其实都是在制造一个闭合的时空轨迹，专业术语叫做闭合曲线(闭合曲线一般是普通物质通过的，所以上面四种应该具体称为闭合类时曲线)。
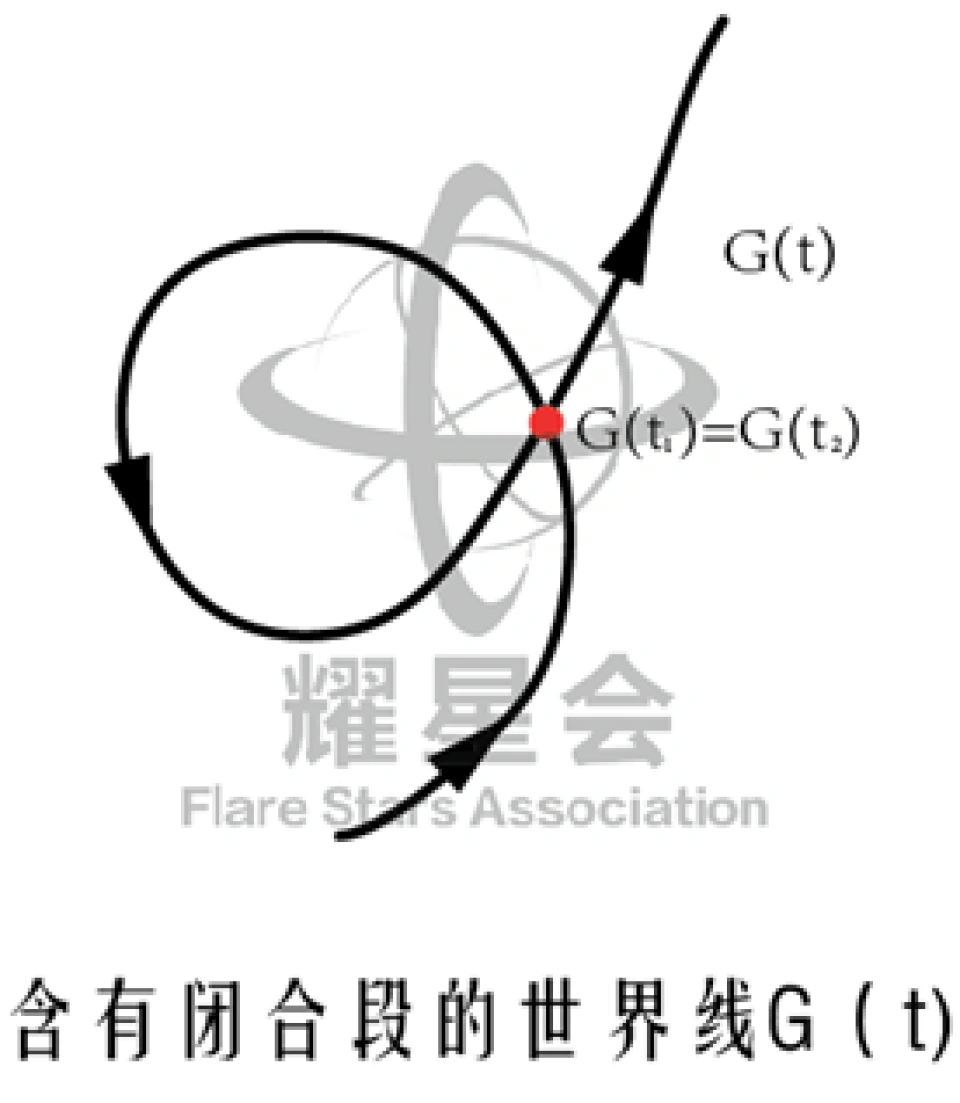
那么什么叫闭合曲线？
你可以把它当做物体在时空中的轨迹。
如图所示，这是在时空中闭合打结的曲线中，重合的地方意味着同一个物体在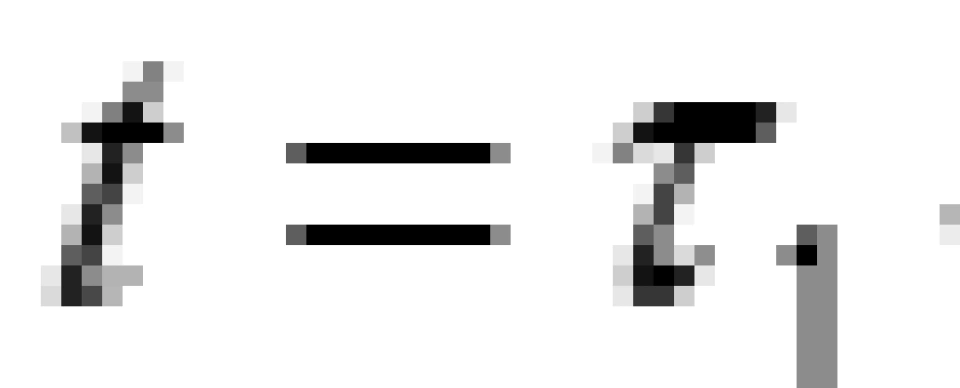
与
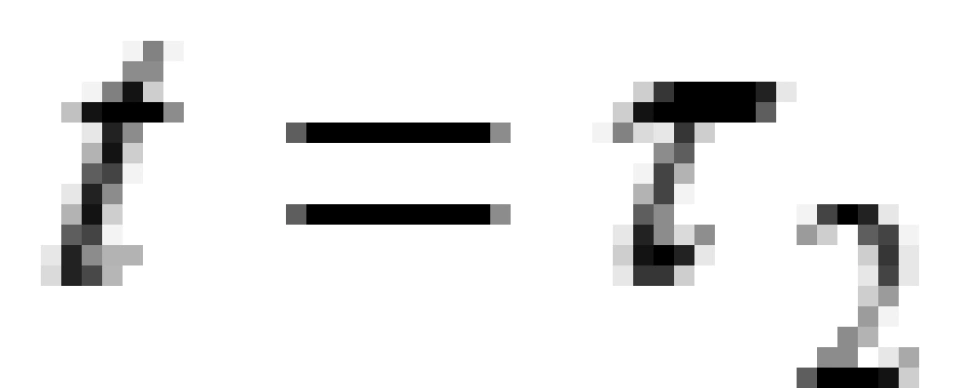两个时刻相遇或者处于同一个事件。
如果这个物体是一个人，那将意味着同一个人在10岁和50岁的时候会相遇，并且处于同一个时空，这就是妥妥的穿越时间。
上述四种时间机器模型本质上都是因为这个闭合曲线。
谈到这里，为了你们后面能够听懂我在讲什么，现在简单地介绍一下相对论的数学基础。
闵可夫斯基几何
在经典力学的绝对时空观中时间和空间是绝对的，不受物体的运动和分布的影响，当然在坐标系变换中是一对不变的量。 但是它们在相对论中却不是这样的。相对论中，时间与空间受到物质的分布和运动影响。
在狭义相对论中时间与空间受到物质的运动影响，也就是说时间与空间在坐标变换中是变化的量。那么存不存在一个量在坐标系变换中是一个不变量呢？也许可能存在，那我们先来找一下。
最先，我们要讲两个相对论的术语，另外，提出光速不变原理，并把它当作是绝对成立的基础假设。
事件：就是在某一地点，某一时刻发生的事情。因此也可以被当成一个时空点。
世界线:用于确定物体在时空中位置的线称为世界线。也可以说是物体在时空中的轨迹。
世界线总是依赖于观察者的。两不同观察者对于同一物体可能会画出完全不同的世界线。飞机上的人和地面上的人观察自由落体会发现轨迹不同，就是这个道理。
现在考虑两个相对运动的惯性参考系，(为了方便计算，我们考虑特殊情况，沿着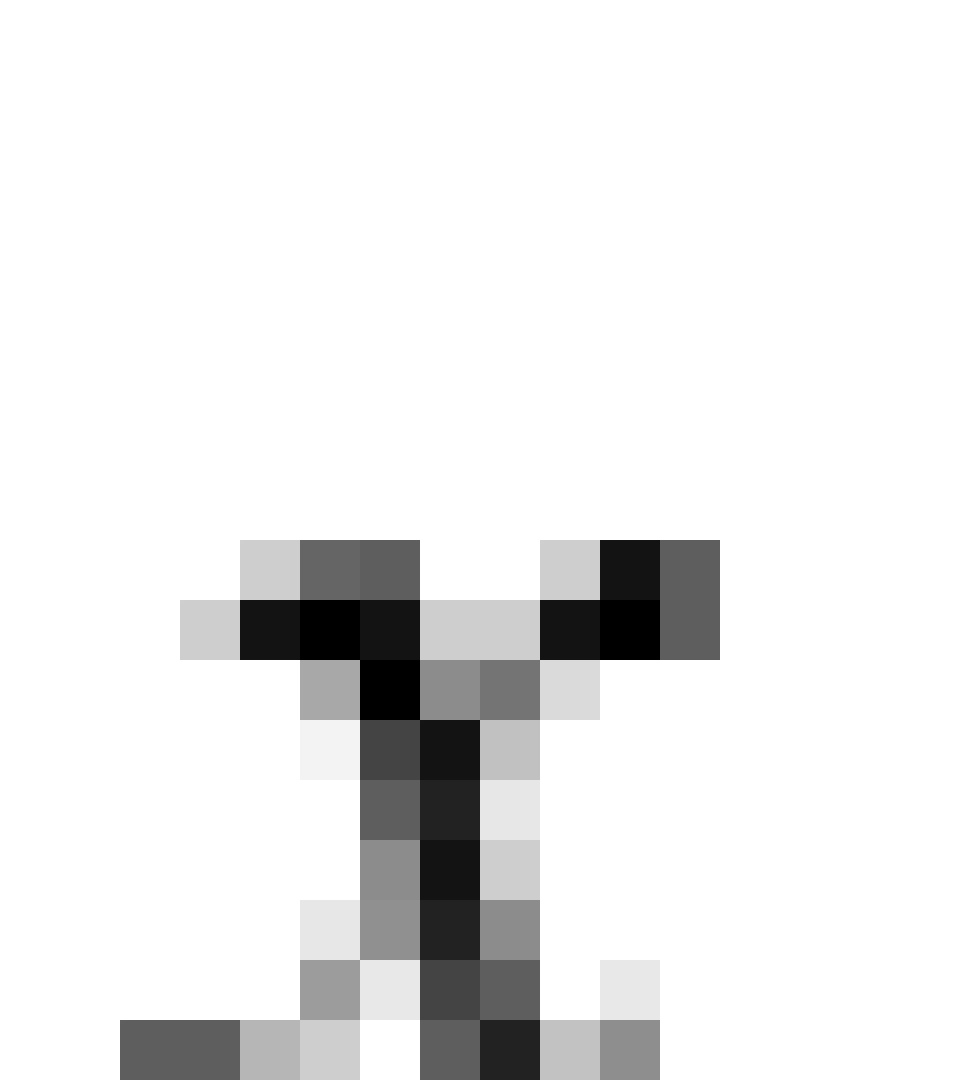
或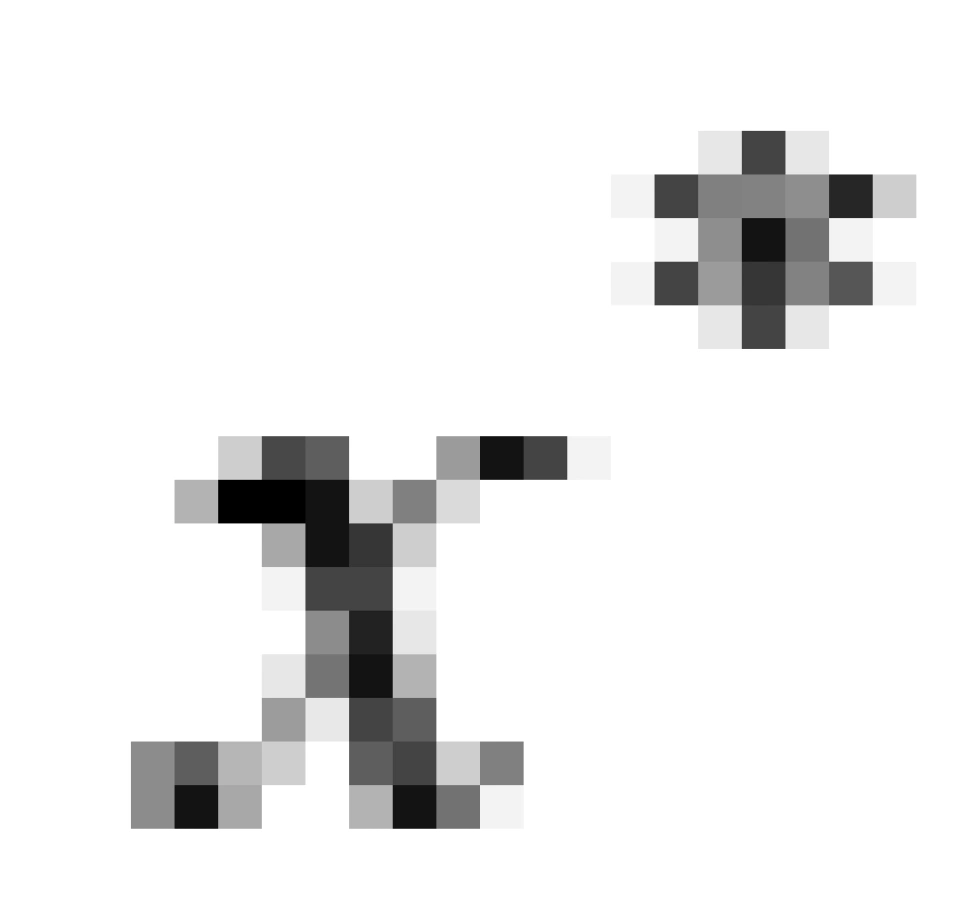
方向运动)它们分别是
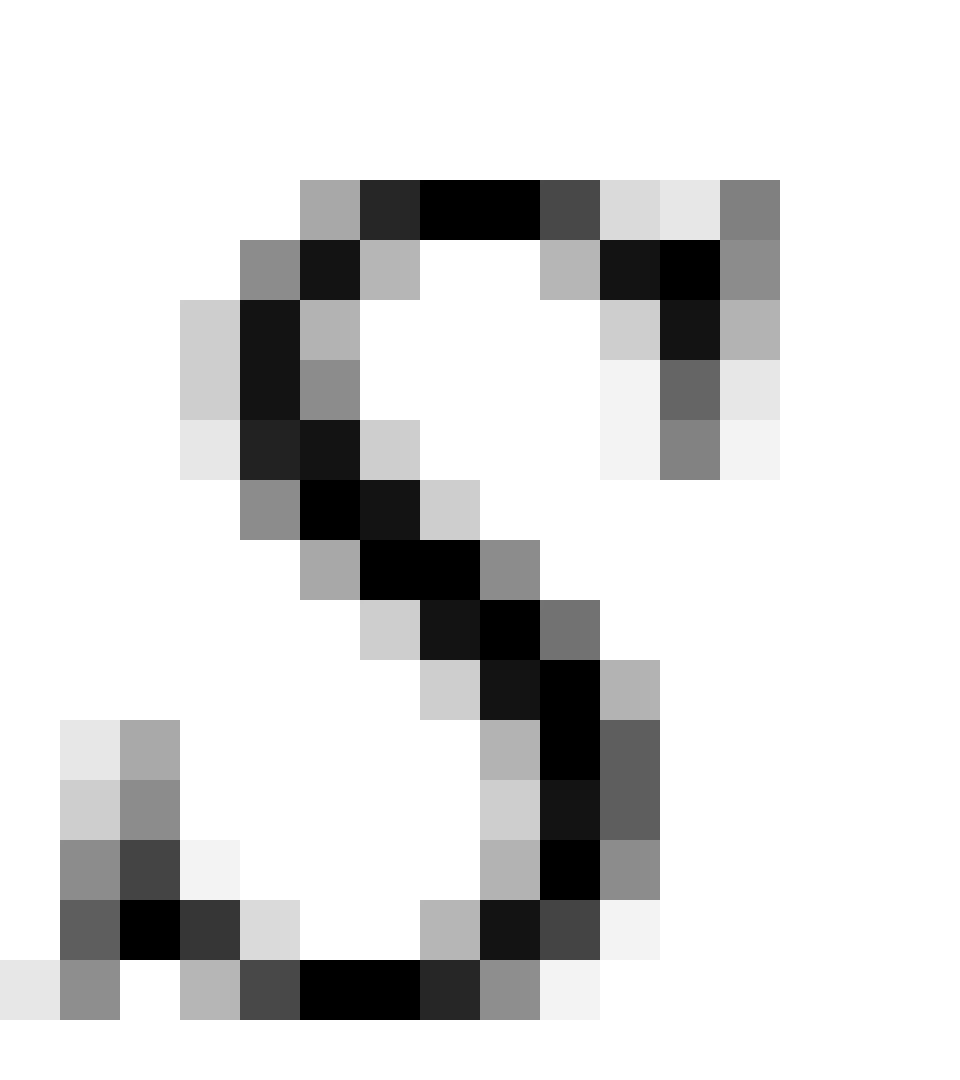系与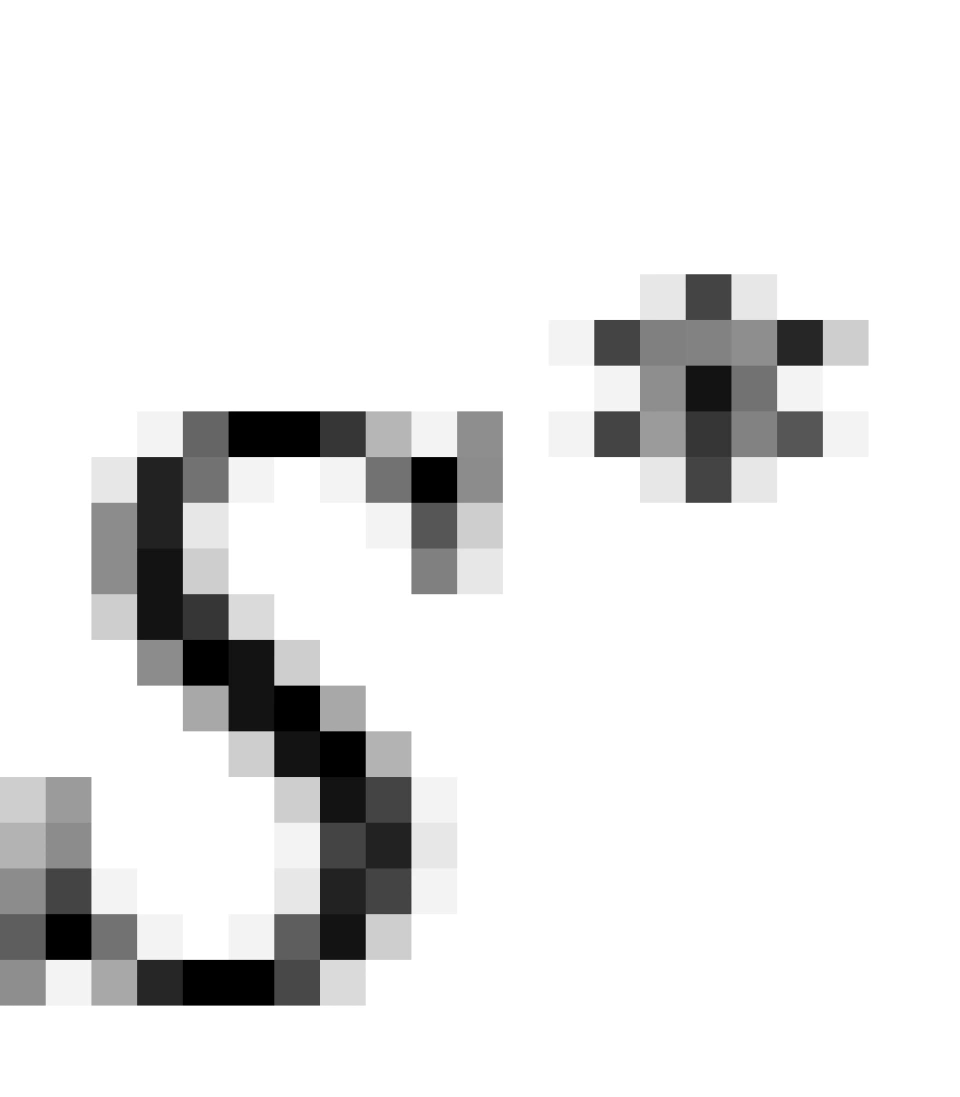
系，两者之间的相对速度是V。
P点与 Q点是光传播过程中的两个相邻的事件，现在我们研究这两个事件之间光的传播速度。
在S系中，
。
则有：
仔细观察上面两个结果，我们不难发现：
因此，我们就找到了一个不随坐标系变换而变化的量。
这只是对于光来讲，是否对于任意两个事件都会有这种可能呢？
这个可以被证明出来可以推广到任意两个事件。
但是，自然界运动并不是匀速直线运动(惯性参考系)，不过我们
只要把时间取得足够短(无穷小)，就可以近似当成惯性参考系来处理。
此时，
。
所以上式就可以改写为:
我们将此定义为任意两个事件之间的间隔元或者是时空线元，记作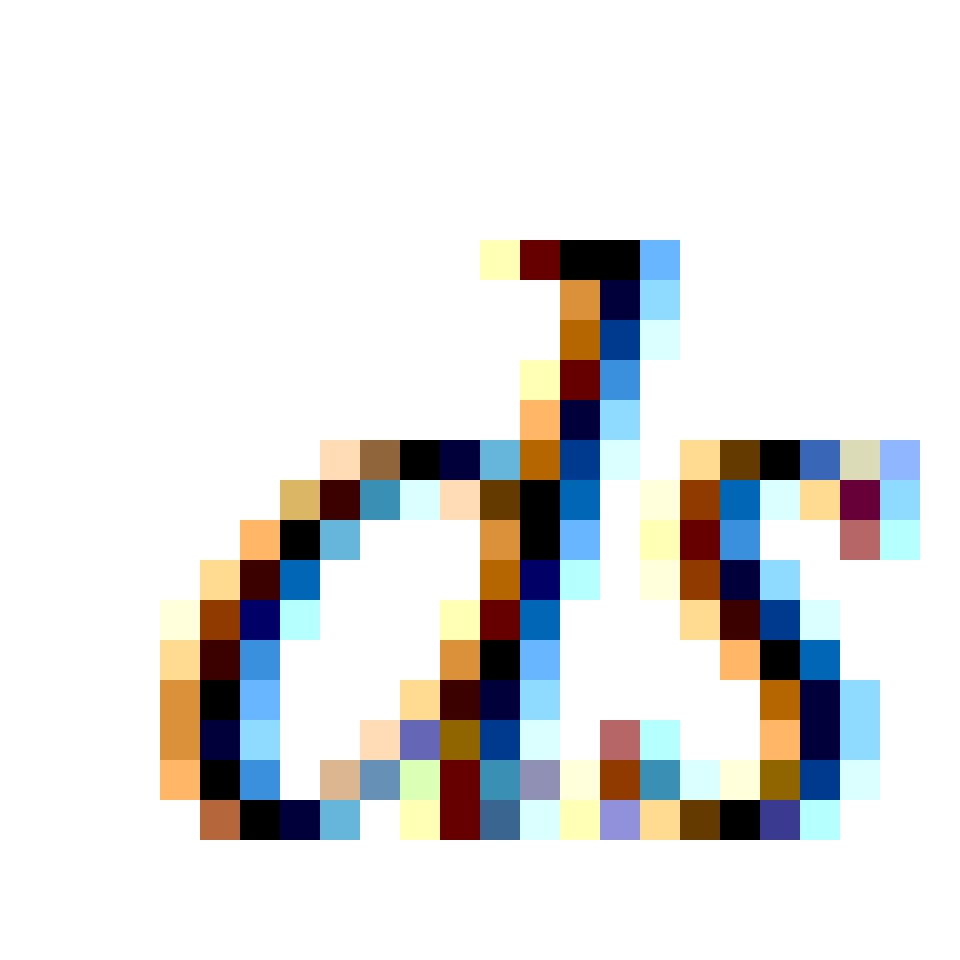
。而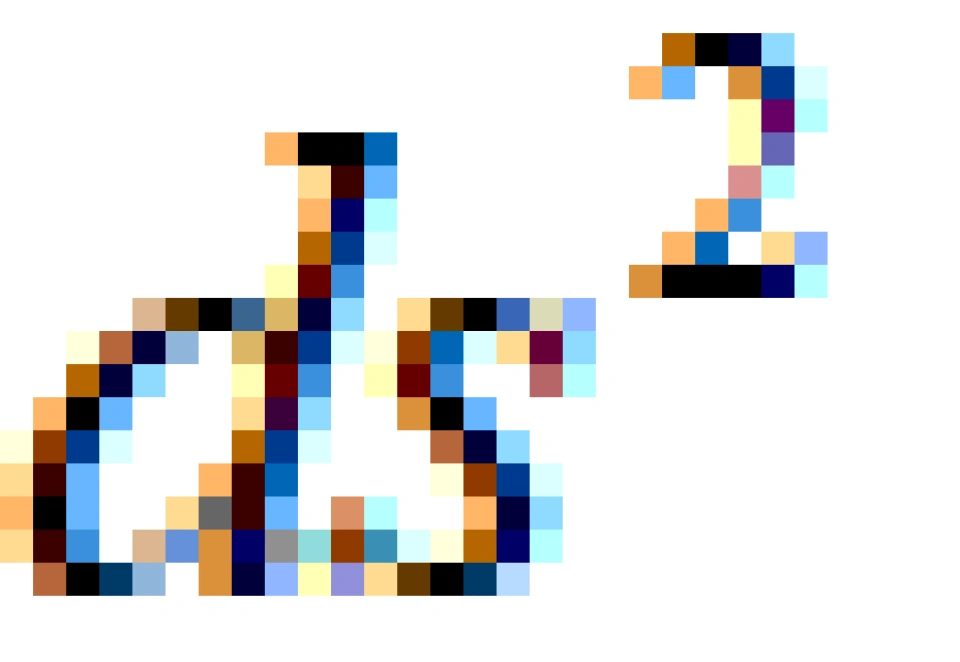
是时空线元的平方。
对于任意的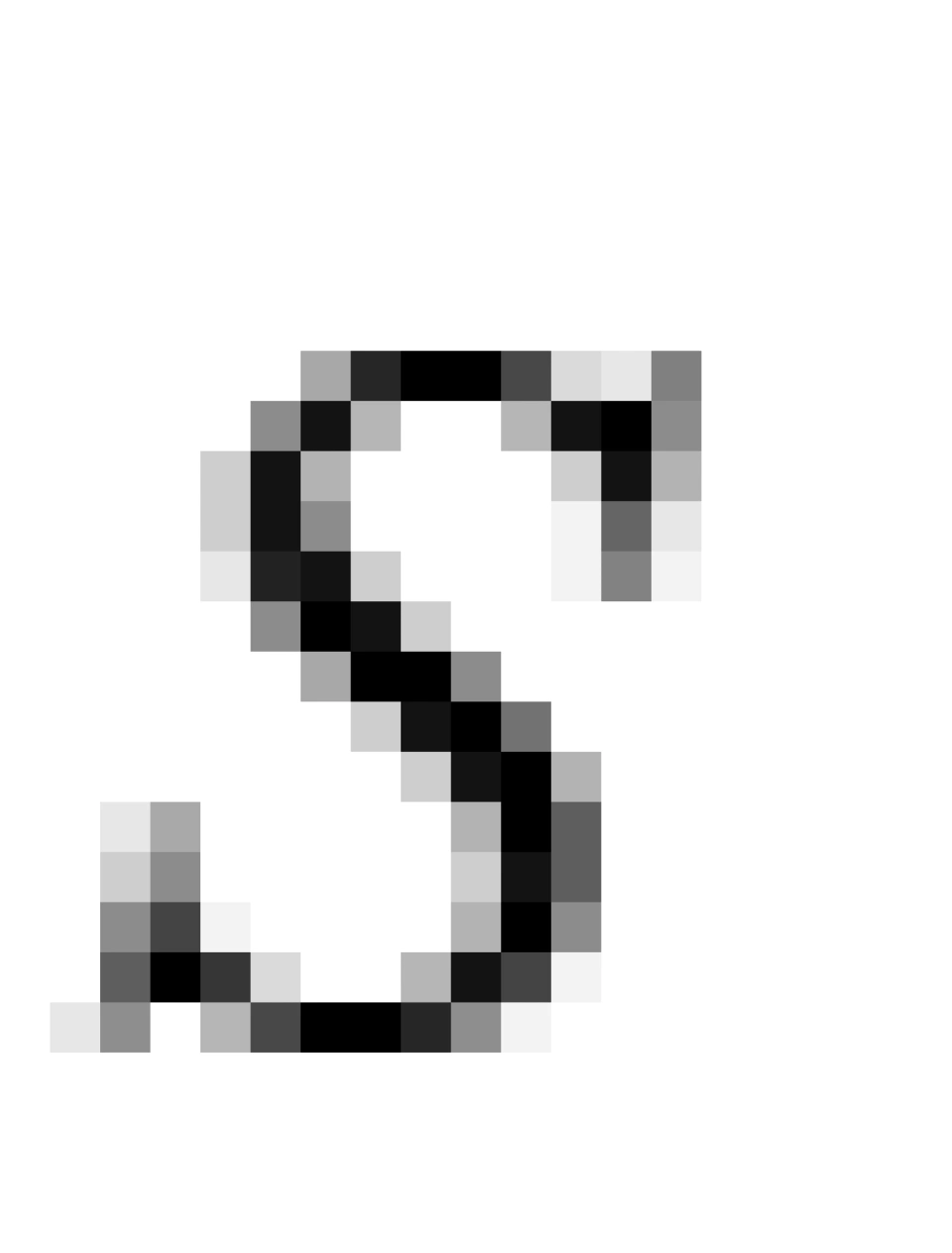
系与
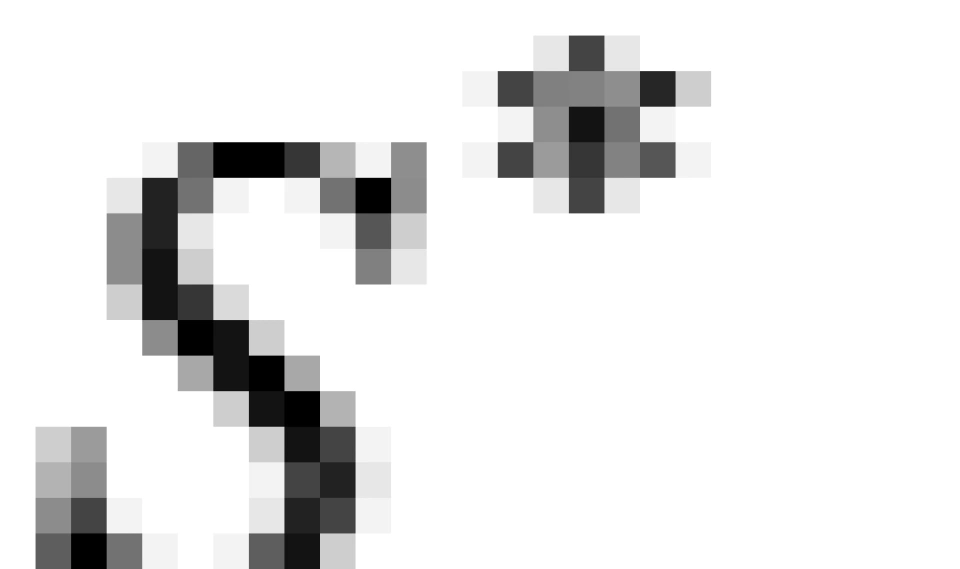系中，P与 Q点光传播过程中的两个相邻的事件之间的时空线元的平方为：
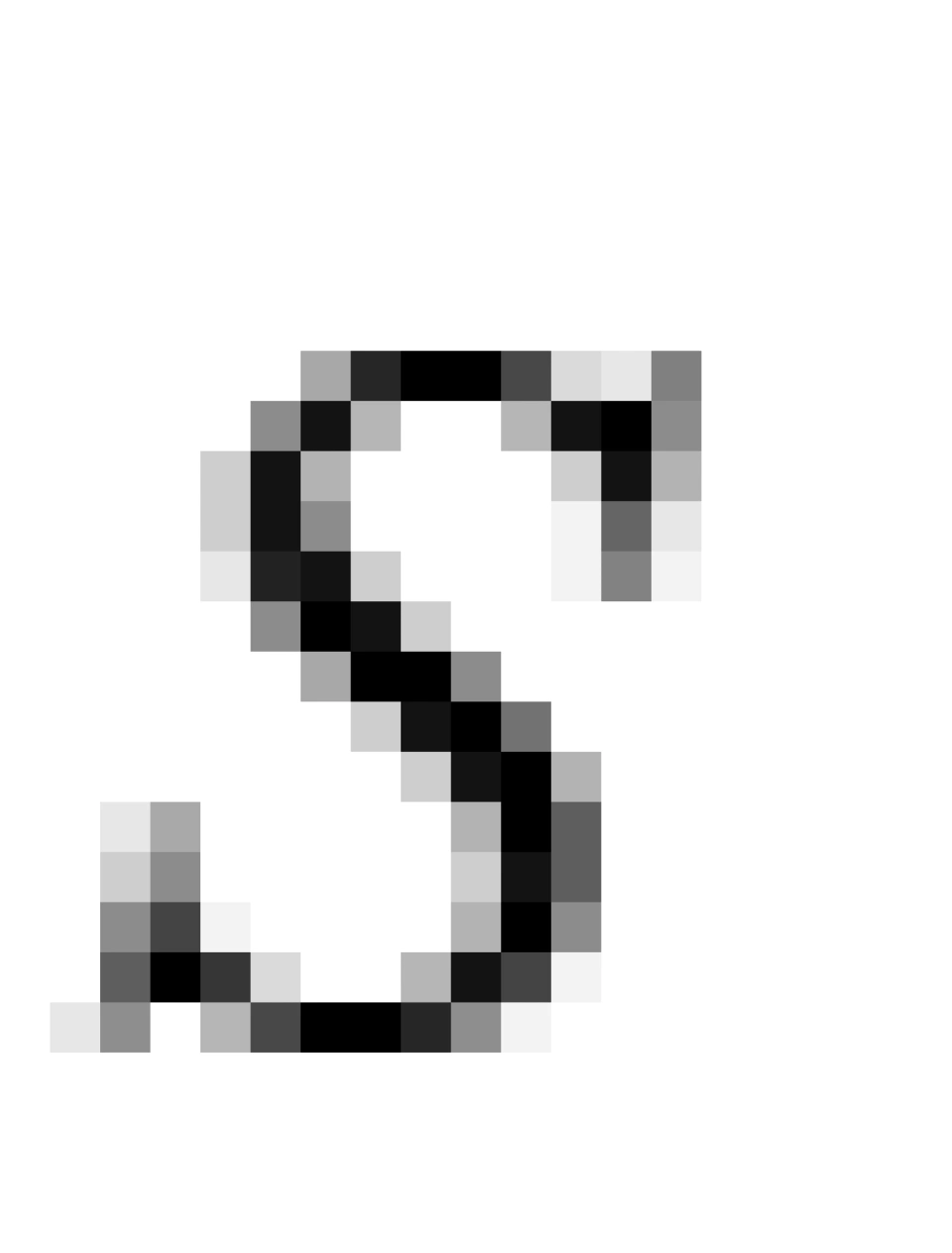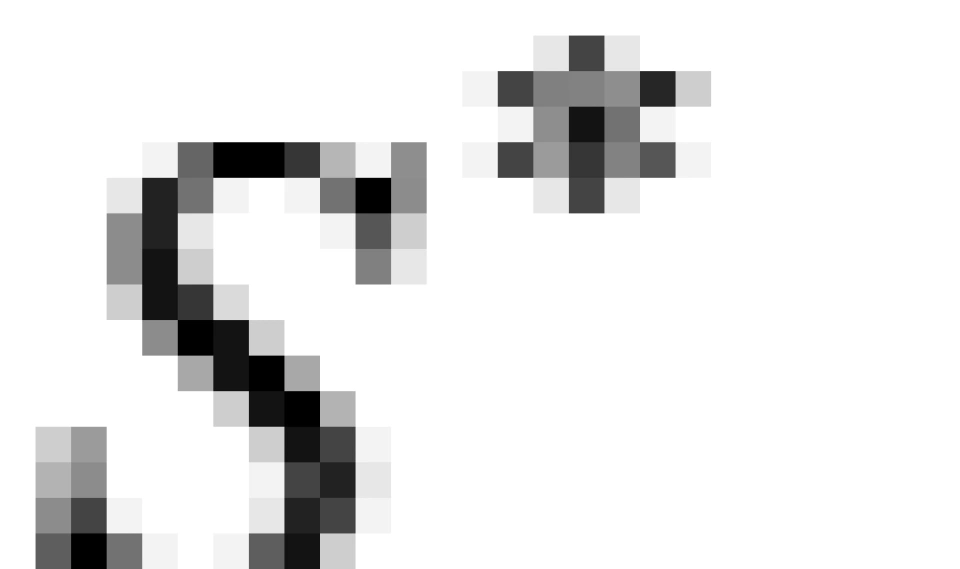由上面可知，对于任意的系与系中，P与 Q点光传播过程中的两个相邻的事件之间的时空线元的平方相等：
它不随惯性参考系的选择而变化，是我们找到的一个不变量。
正是因为这种时空间隔不变性，我们可以把这个不变量当做一个几何量并采用几何的语言去描述物理时空。
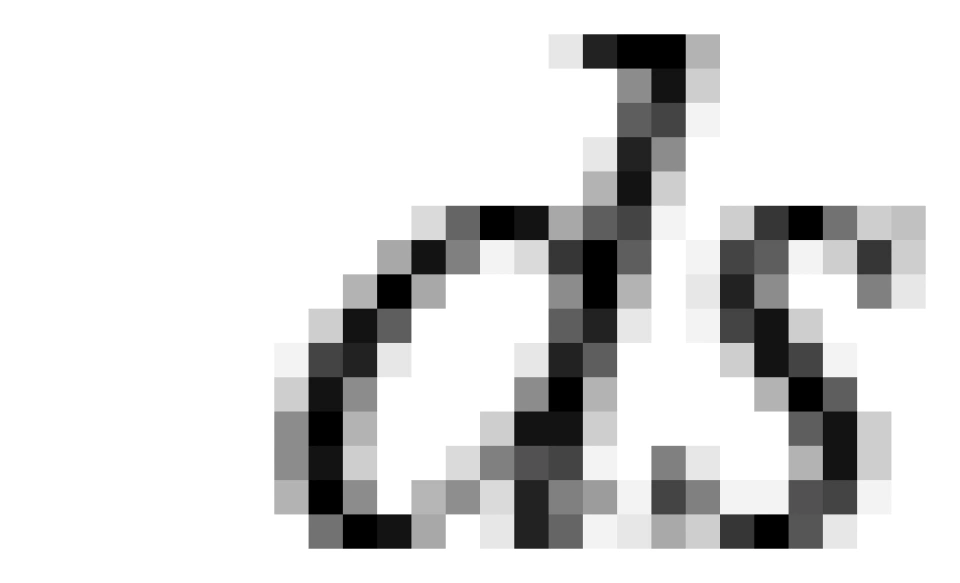代表的是两个事件之间时空的间隔，你也可以把它类比成空间中两点的距离或者间隔，只不过这里是在四维时空中两个事件之间的距离。这个量是不随参考系的选择而变化的，也就是不随观察者而变。
由于不变量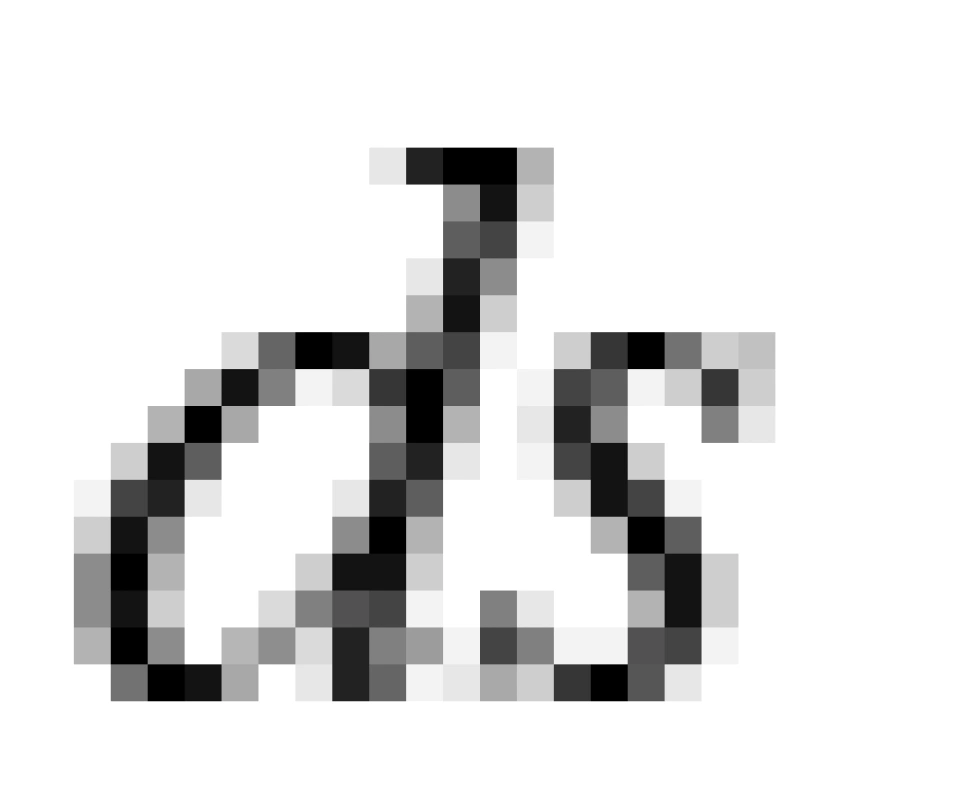
的平方可以带有负号，这意味着对于时空中的两个事件，
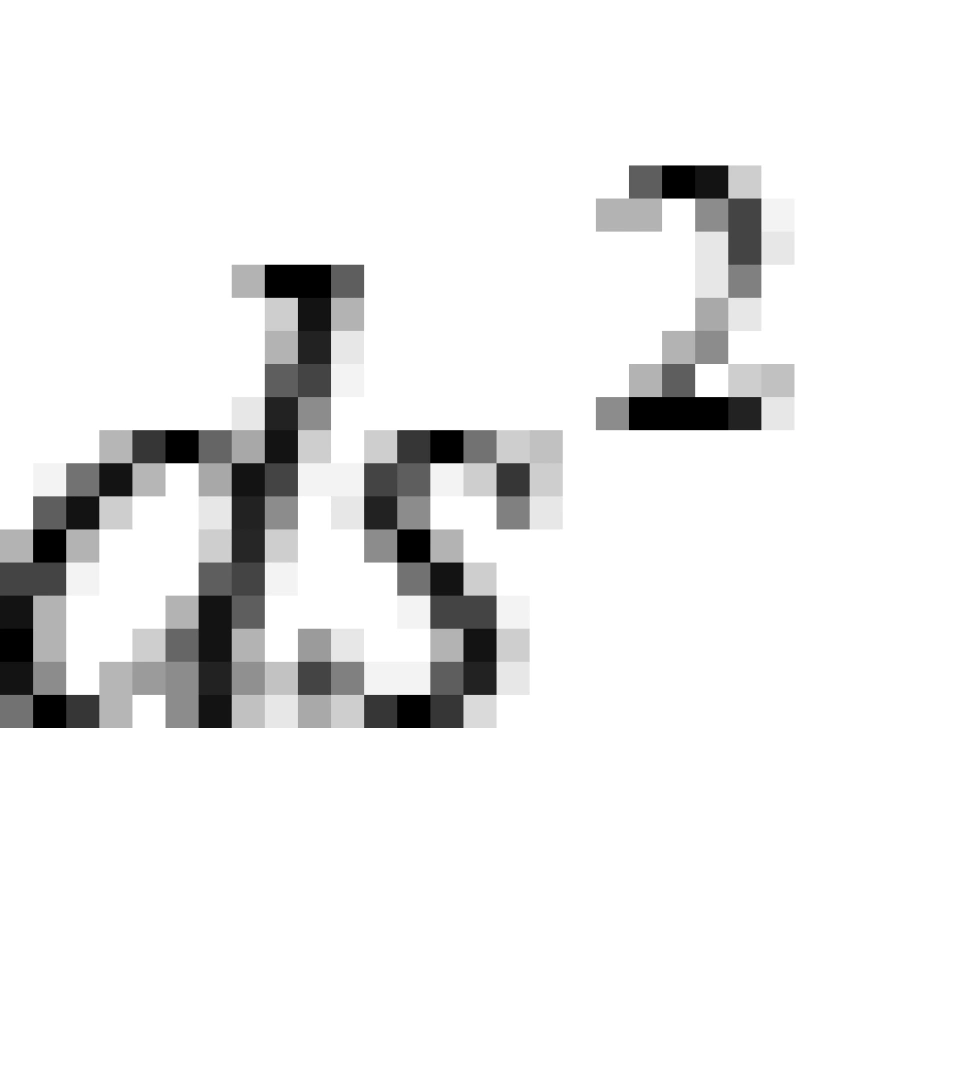的值可正可负可为零。
因此，我们可以分类：
，我们称之为类时曲线，
，我们称之为类光曲线；
，我们称之为类空曲线。
类时曲线就是有静止质量或者速度低于光速的物体运动时的世界线。这里，对于任意两个事件，你都是可以建立因果关系的。
类光曲线就是静止质量为0或者速度等于光速的物体运动时的世界线。任意两个事件之间，也是可以建立因果关系的。我们就是通过这一特殊的情况来推出惯性参考系变换有一个不变的量。
类空曲线就是静止质量为虚数单位或者速度高于光速的物体运动时的世界线。不过，在狭义相对论的框架之中，这个是没有任何意义的，因为两个事件之间无法建立因果联系。
对于我们找到的这个不变的量 ，我们给出的解释是时空中两事件的距离，或者叫做时空间隔，它与我们通常所熟悉的空间间隔不同，它也考虑了时间间隔。
所以闵可夫斯基才说：从现在起，孤立的空间和孤立的时间注定要消失成为影子，只有两者的统一才能保持独立的存在。 完美地将时间和空间统一在一起，让整个时空变成绝对的了。而时间和空间就像矢量分量一样，在不同的坐标系下分量不一样，但是时空的间隔就类似于矢量的模长在变换下不变。
我们将采用过去的记法去重新写一遍这个不变量，但是在讲这个之前，首先要介绍一个新的概念—-度规。
度规
度规度量也可以看成是一种测量的标准。好比各个国家有各自的货币，不尽相同。它其实是定义了在一个坐标系中如何度量曲线的长度。
建立坐标系，把每个点的坐标都写下来，用两点之间距离公式来计算距离。
现在我们考虑二维的情况下，我们采用平面直角坐标系。选取任意两点P，Q并且写下他们的坐标：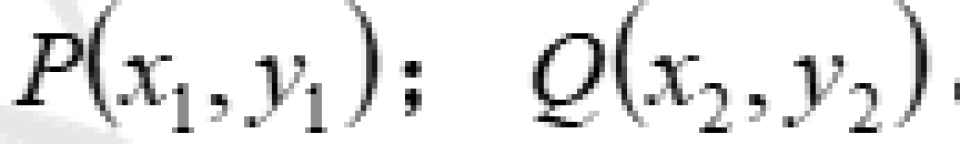
。
那么我们可以很容易利用两点之间距离公式来计算P，Q之间的距离。
这是不是很像勾股定理，其实它就是勾股定理。
如果计算曲线，也可以用勾股定理，只要曲线分成很多段，每一段近似看成是直线，然后用勾股定理把每一段的长度计算出来，再把每一段长度累加起来，只要把
取得足够短(无穷小)，就可以当成是曲线的长度。
此时，
。
所以上式就可以改写为:
知道两点坐标，除了用两点之间距离公式来计算P，Q之间的距离，还可以用
上式中的
矩阵，被称之为二维欧几里德度规。
按照上面的在二维平直空间中的讨论，我们也将结论扩展到三维平直空间中，构造出三维欧几里德度规。
在三维平直空间中,采用直角坐标系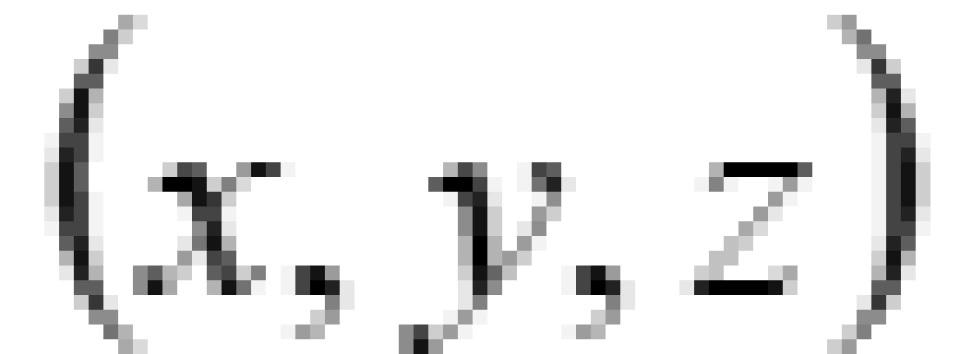
，任意两点之间的距离
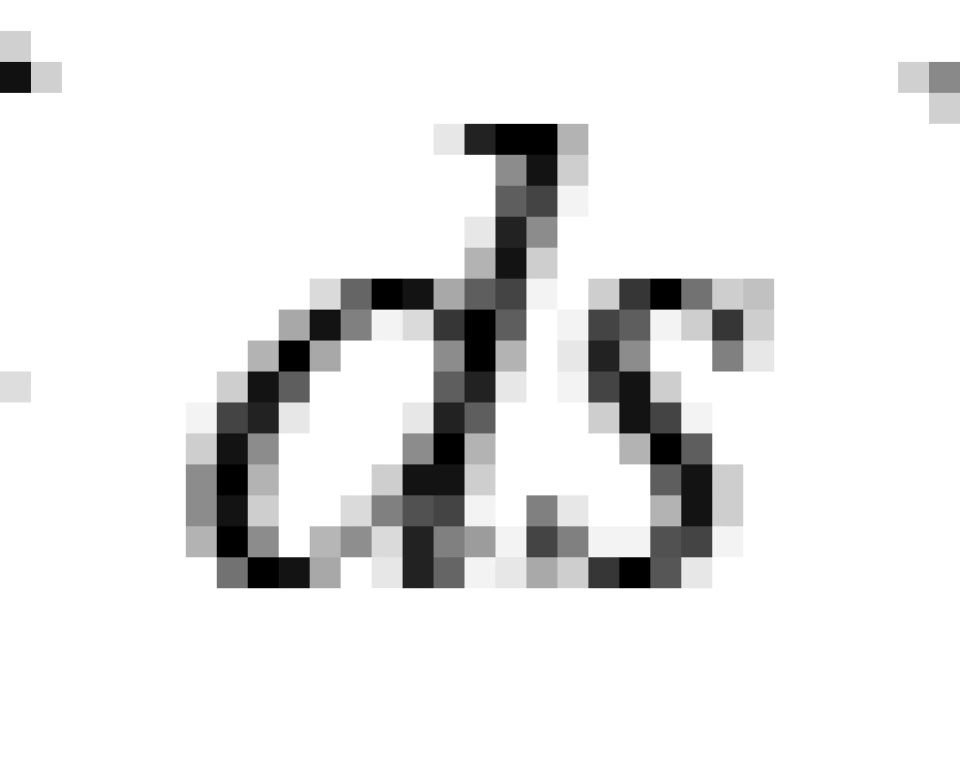可表示为：
上式中的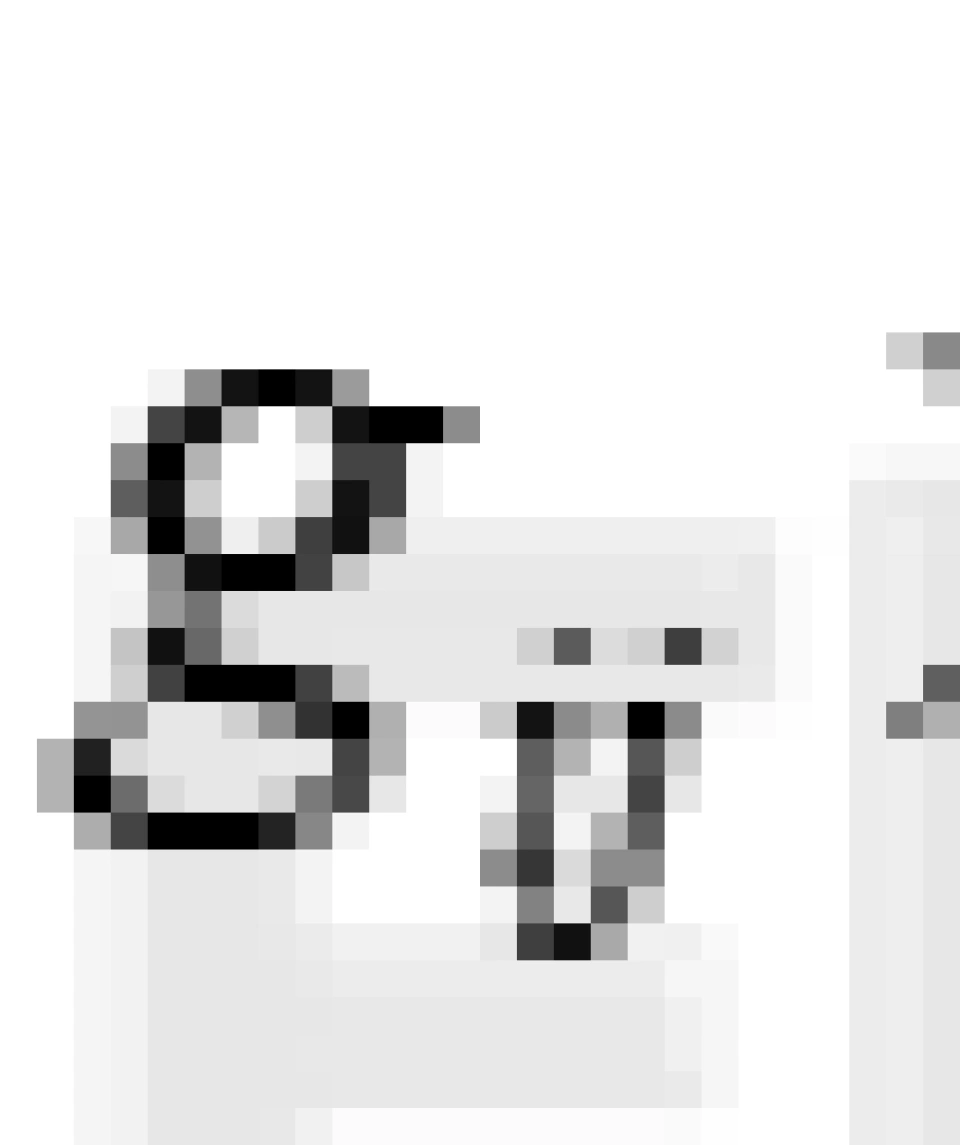
是3X3矩阵，被之为三维欧几里德度规（三维欧几里德度规在笛卡尔坐标系下的形式。）
如果选用球坐标系
, 任意两点之间的距离
则为：
上式中的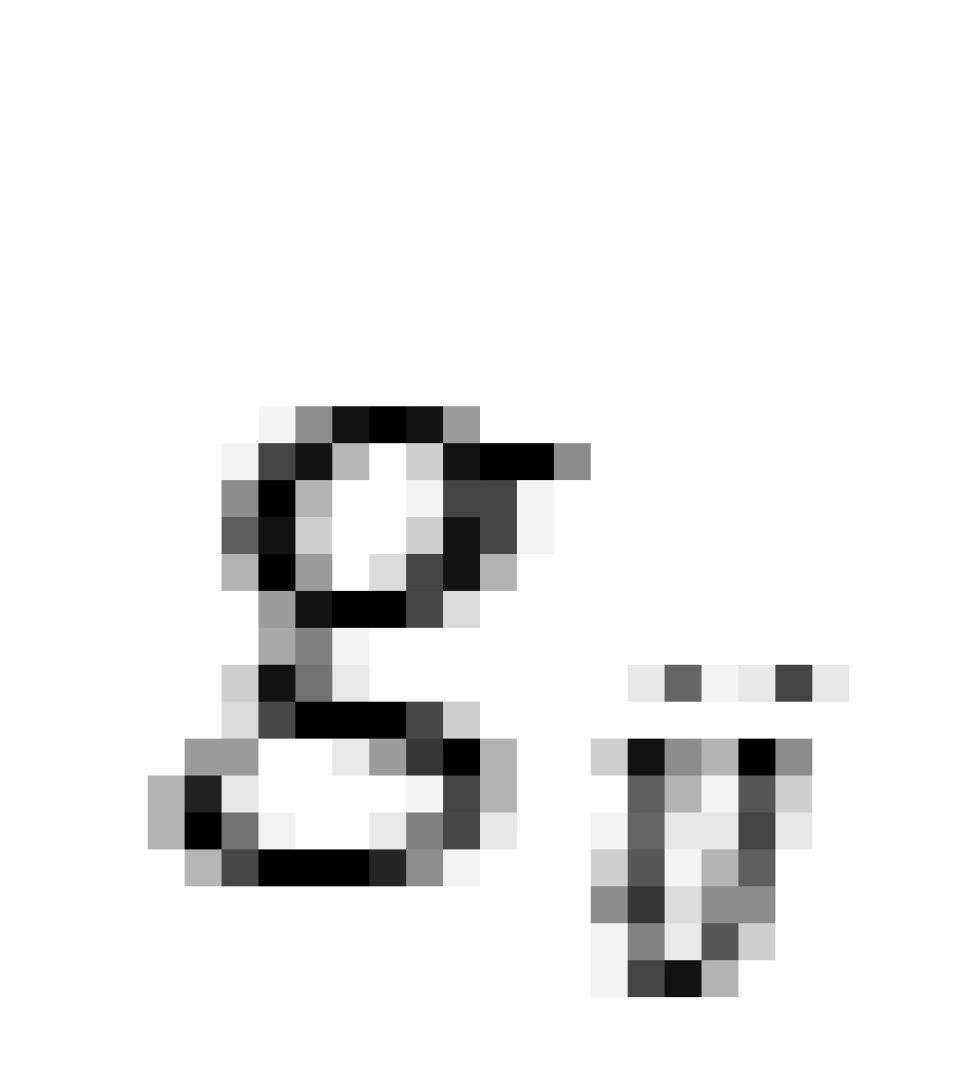
是3X3矩阵，是三维欧几里德度规在球坐标系下的形式。
可以看出不管采用何种坐标系，两点之间的距离是不变的。而我们上面得到的那些矩阵就称之为度规，它是在坐标系之中去度量两点之间距离的，通常是矩阵形式。
当然并不是所有度规都是必须只有非交叉项（主对角元素）不为0，其他项(交叉项)皆为0。学过线性代数的人一定知道，有些矩阵是可以化为正定形式的亦即主对角元素不为0，其他项皆为0。
度规这个概念可能很难理解，下面来举个例子。
比如，把一个个区域类比成一个个国家，用每个国家使用的法定货币来类比能够完全覆盖这个区域的坐标系。每一个区域都使用自己的坐标系（局部坐标系），然后给出当地计算距离的方法。而计算距离的方法就取决于度规。每个国家都使用自己的法定货币，然后给出这些法定货币的数目关系。而度规就类似于规定的法定货币的数目关系。
另外，求和符号写起来太麻烦了，我们可以引入一个求和约定去除这个求和符号。最早由爱因斯坦规定，所以被称之为爱因斯坦求和约定(这被爱因斯坦私下戏称为自己对数学的最大贡献)。
我们下期继续介绍。
【本文为耀星会的原创作品，未经允许，禁止盗用、转载、篡改文章，否则耀星会和作者将追究版权责任。】
