朋友们,大家好。笔者即将开学,在繁重的学业压力下想来没有太多时间精力,也没有足够的学识去肝深度的黎曼猜想。思来想去,还是决定发这一篇科普性质的文章,从 ζ 函数本身以及 ζ (2) 的计算两个切口去瞧瞧 ζ 函数与素数的关系。希望读者能够谅解,谢谢。
1、调和级数与质数个数间的关系
话说欧拉大神一天闲的无聊,想用自己的方法证明质数的个数有无限个,他想到:如果用 p 来表示质数,那就可以构造等比数列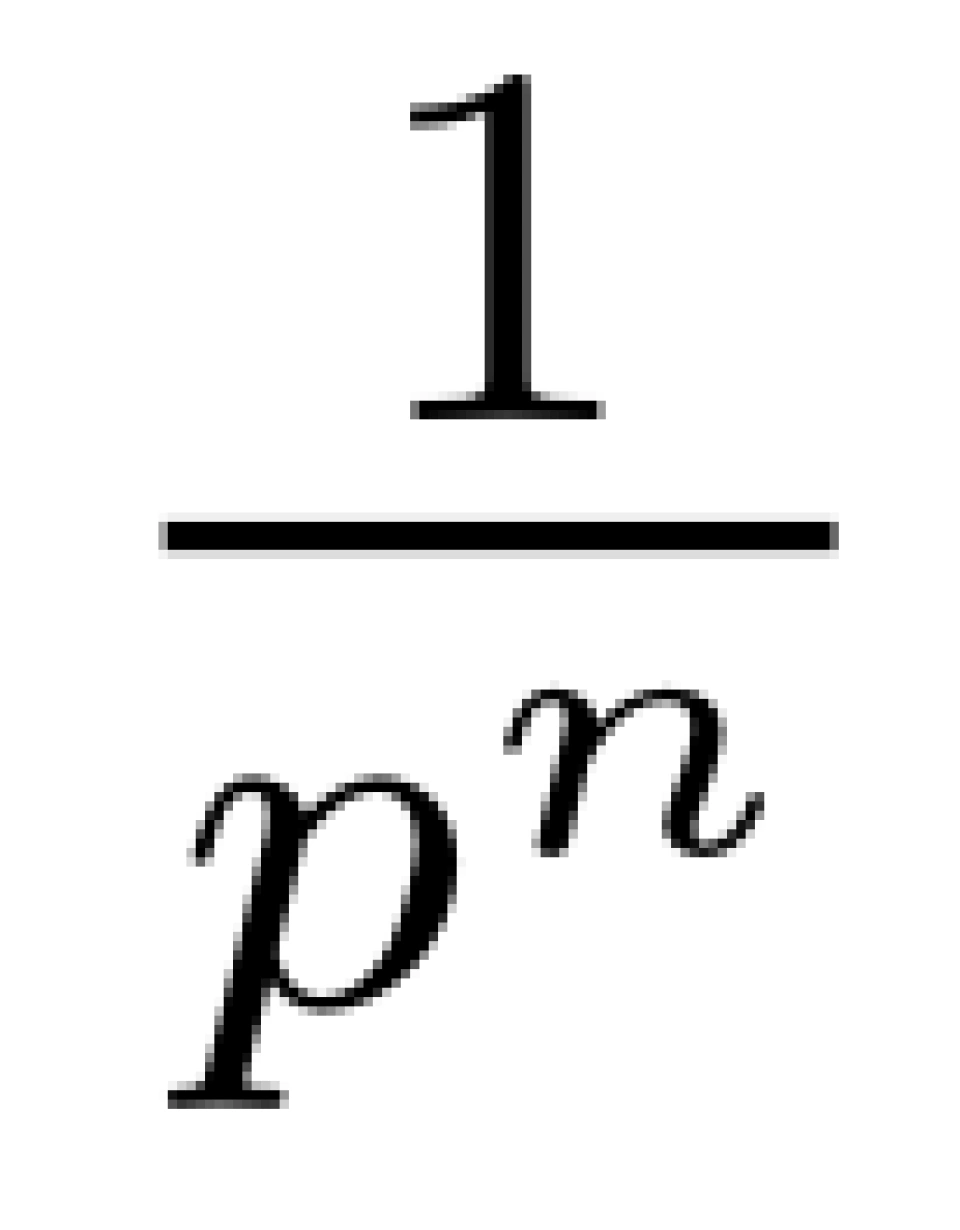 ,将其求和,就有
,将其求和,就有
由质数的定义我们知道,所有的正整数由 1, 质数,以及质数间的乘积构成。所以,上述计算式的结果是就是分母中包含所有正整数的调和级数,即
由于调和级数是发散的,而对于每一个 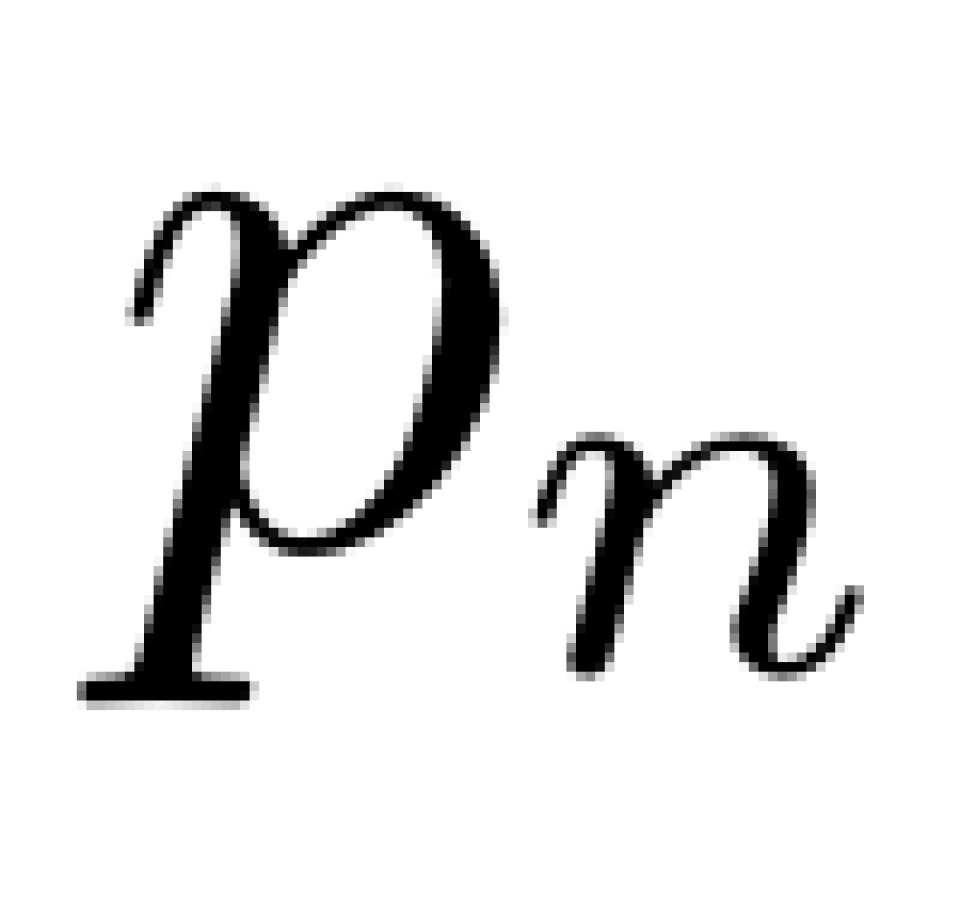 ,都有
,都有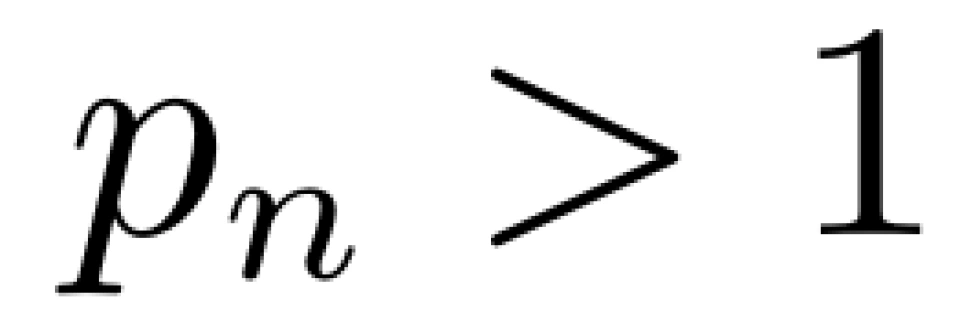 ,所以每个
,所以每个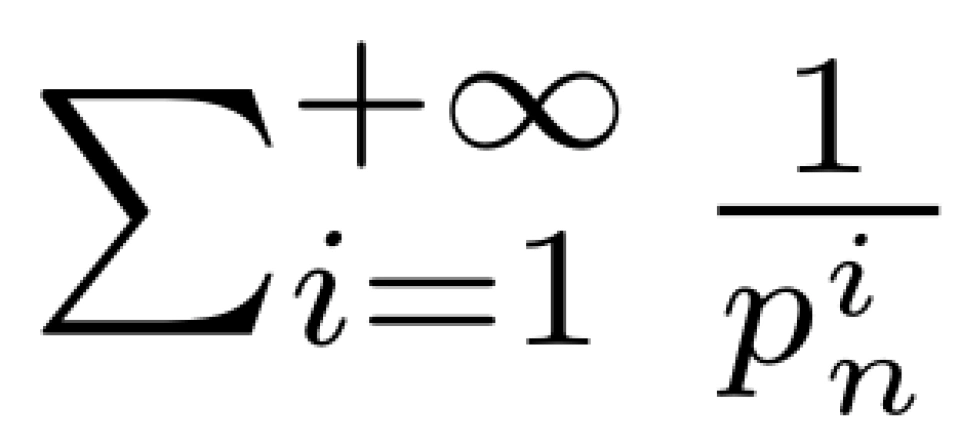 都会收敛到
都会收敛到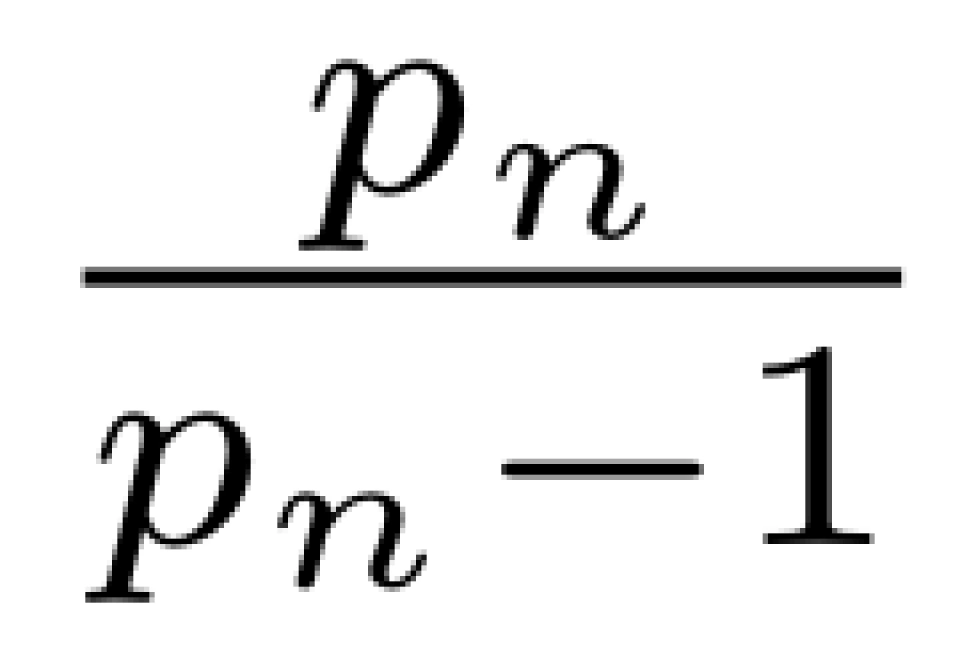 ,如果质数只有有限个,那么左式将只有有限个常数相乘,这与调和级数发散的结论不符,因此可以推出,质数有无限个。
,如果质数只有有限个,那么左式将只有有限个常数相乘,这与调和级数发散的结论不符,因此可以推出,质数有无限个。
2、欧拉的推广 (该内容参考自妈咪说 Mommy Talk@www.bilibili.com)
欧拉通过上面的推导得到了如下等式
于是,欧拉定义,
上述操作如同一个筛子,把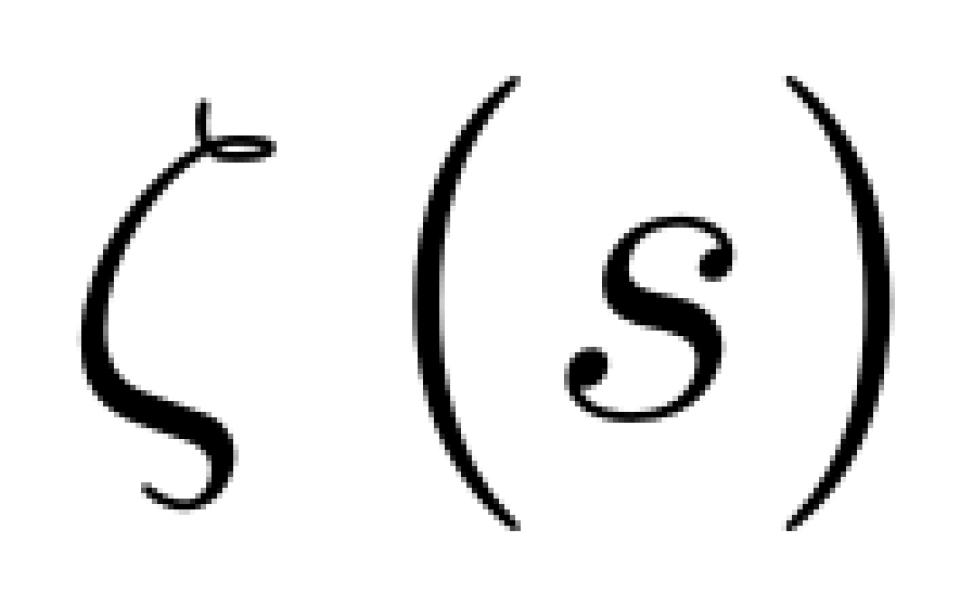 分母中含2的倍数的项筛掉了。对上式用
分母中含2的倍数的项筛掉了。对上式用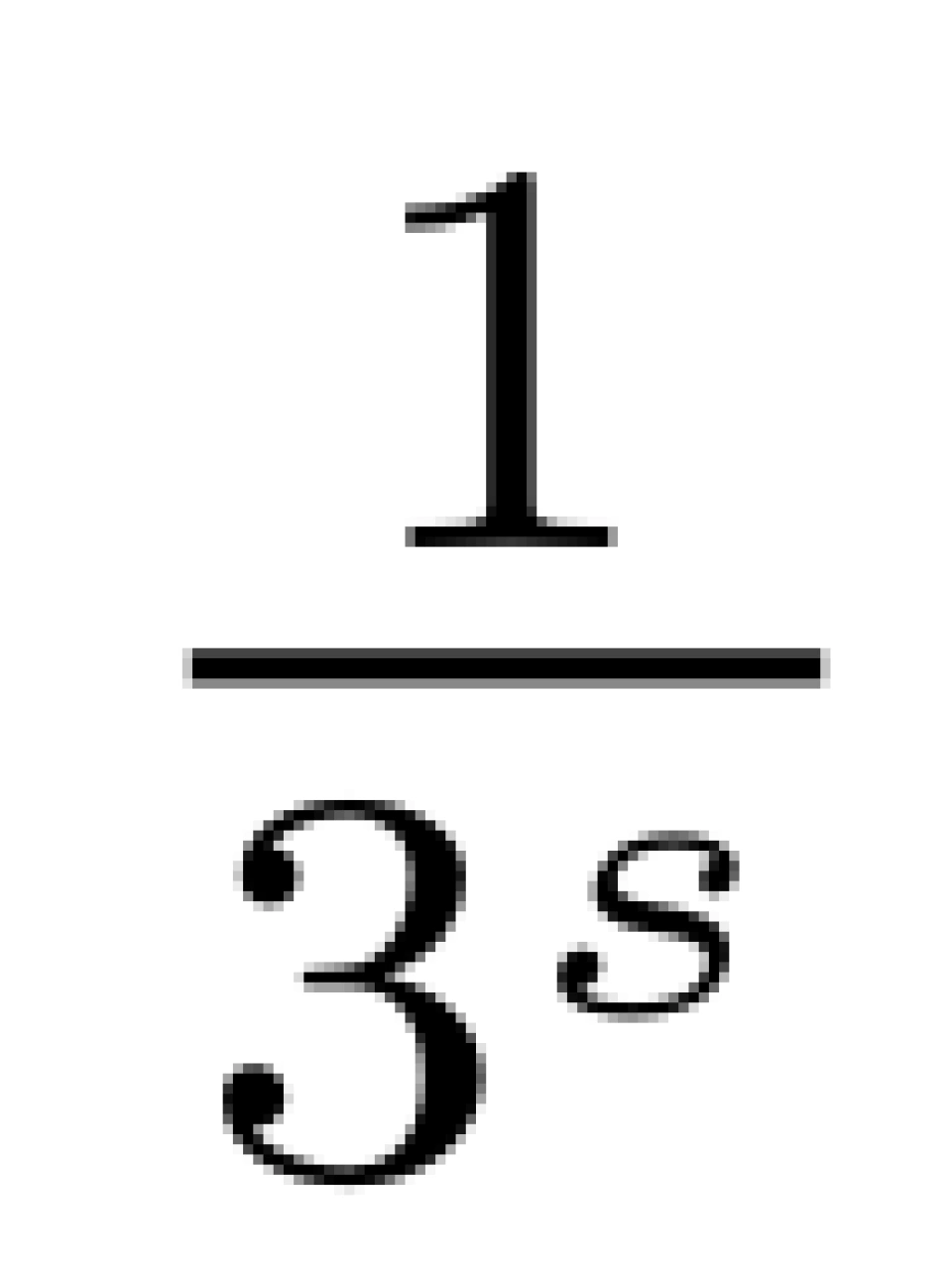 如法炮制,得
如法炮制,得
……
这项操作有一个形象的名字,叫质数筛。当对所有质数进行上述操作后,,分母中所有质数及其倍数都被筛掉,等式右边只剩下 1 s 这一项,我们
就得到了大名鼎鼎的欧拉乘积公式
或
3、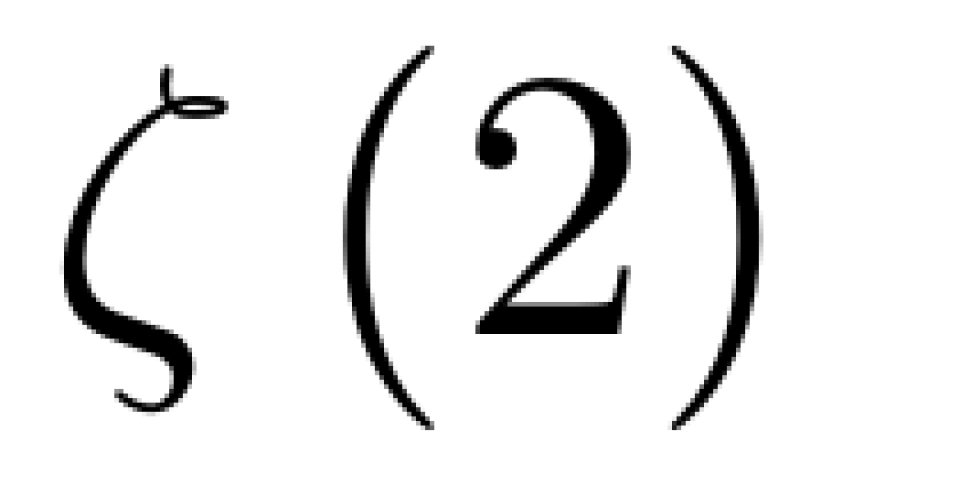 (巴赛尔问题)的求解及应用
(巴赛尔问题)的求解及应用
巴塞尔问题是数学史上一个著名的问题,曾难倒约翰·伯努利、雅各布·
伯努利等一系列著名科学家,后由欧拉首次给出正确答案。笔者也希望,这个有名的问题为更多人所知。在这里,笔者给出三种解法,都只需要中学的数学基础知识,但是思维难度不一而同,由易到难,请各水平的读者按需取食。
方法一:对于函数 sin(x) 进行泰勒展开, 有
所以,
同时,我们又知道,函数 sin(x) 的根是 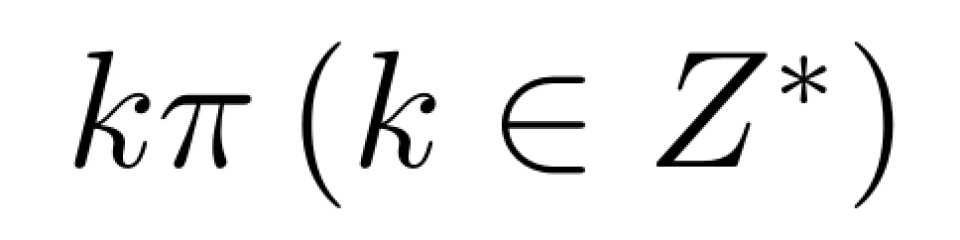 ,所以,我们能得到sin(x) 的另一个形式,即
,所以,我们能得到sin(x) 的另一个形式,即
为了使上下两式相等,对比常数项系数,可得
即
将 A 的值带回原式中,可得:
对比上式与泰勒展开式的二次项系数,可得
解得,
法二:复数积分的证明(此法由 Dennis C.Russel 给出)
考虑积分
由欧拉恒等式得:
代入上式得,
由对数函数性质可将上式变形得,
计算可得,
对函数 f (x) = ln(1 + x) 进行泰勒展开,可得
所以,
而我们知道,
我们又推出,
因为等式左边是实数,等式右边是纯虚数,所以惟有等式两边都等于 0 等式才可以成立,所以解得,
法三:用三角函数的知识求解(此法由 Ioannis Papadimitrion 于 1973年在 American Math Monthly 中给出)
证明:
即
令 n = 2m + 1, 则有
为以下方程的根
由韦达定理得,
引理证毕
同时,由不等式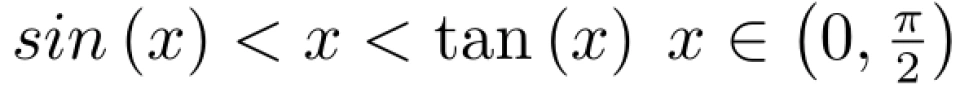 得,
得,
所以,
化简得,
最后,我们来解一道题玩玩,
若从所有正整数中任取两个,问他们互质的概率?(该问题及解答来自孙健老师的视频,视频地址:https://b23.tv/eE0xNb)
不妨设所求的概率为 x,两个正整数 m,n 之间的最大公因子是 k,我们来研究 k 的性质,对于在所有正整数中任意抽取出两个数,并且两数
同时,因为
那么,我们就可以得到方程
解得,
写在最后:短短续续的,笔者终于把自己挖的坑填上了。也相信这篇文章能达到笔者的愿想,从一些角度去侧面窥探 ζ 函数与质数间的关系。其
实,不经过深挖与思索,很难看出,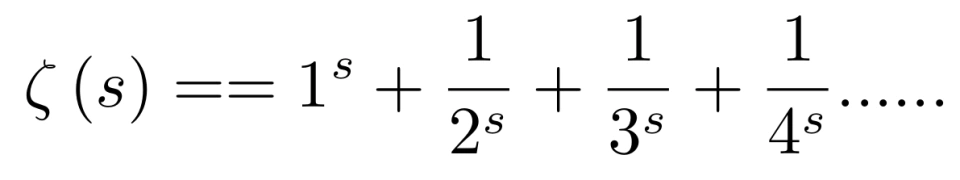 这个级数会与质数以及圆周率π有千丝万缕的联系。但是,数学之美是上帝早就设计好的,只等待我们去不停的发掘。黎曼 ζ 函数是属于复分析领域的内容,而黎曼大神,也是复分析现代形式的创立者。如果这篇文章能够让读者更多的窥探 ζ 函数与质数的关系,激发读者对于数学的兴趣,那它的目的,也就达到了。
这个级数会与质数以及圆周率π有千丝万缕的联系。但是,数学之美是上帝早就设计好的,只等待我们去不停的发掘。黎曼 ζ 函数是属于复分析领域的内容,而黎曼大神,也是复分析现代形式的创立者。如果这篇文章能够让读者更多的窥探 ζ 函数与质数的关系,激发读者对于数学的兴趣,那它的目的,也就达到了。
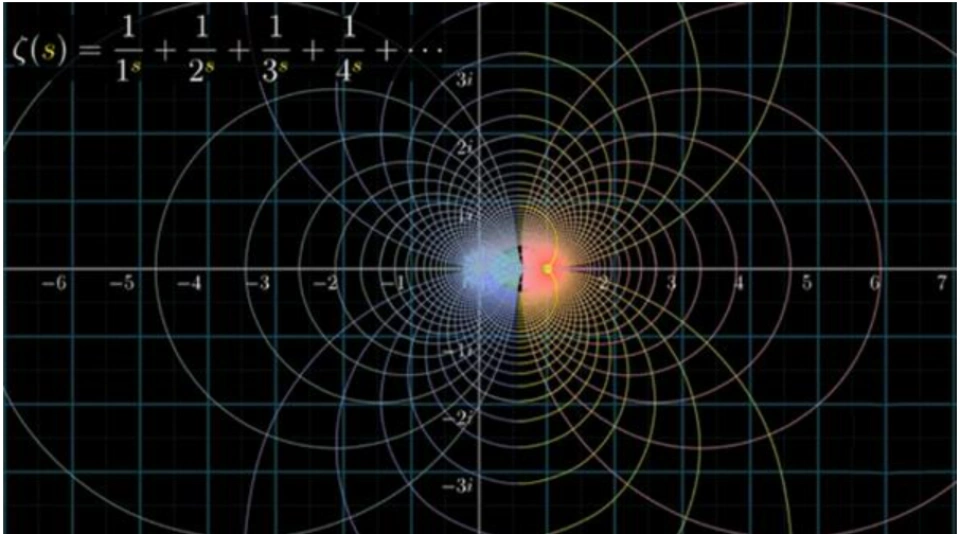
最后,放一张 ζ 函数美丽的函数图像:
谢谢! ![[s-70]](https://www.bokeyuan.net/pic/image/emoji/cas/70.png)


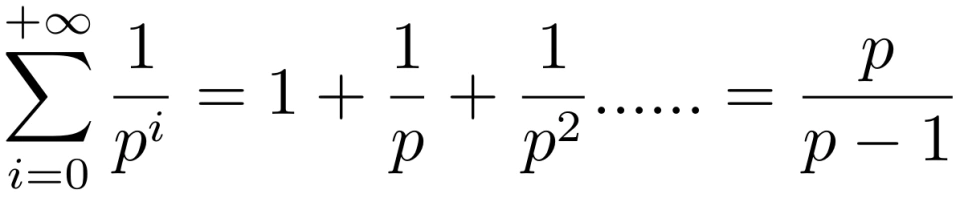
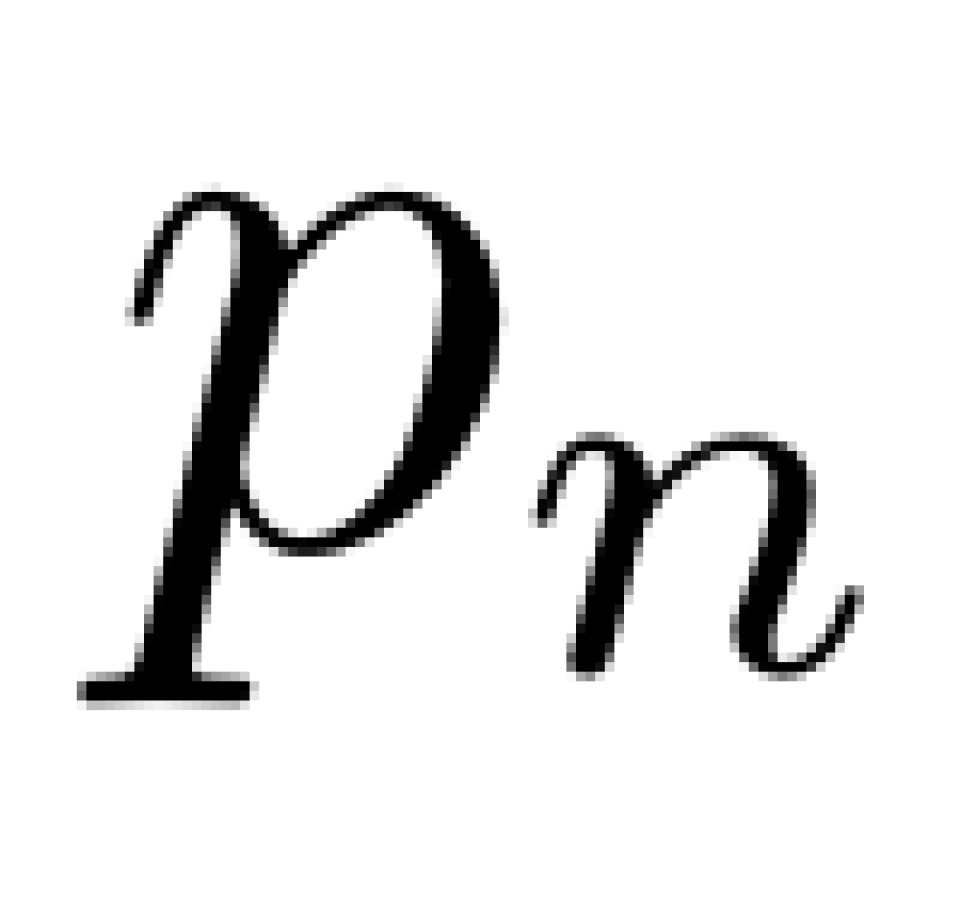
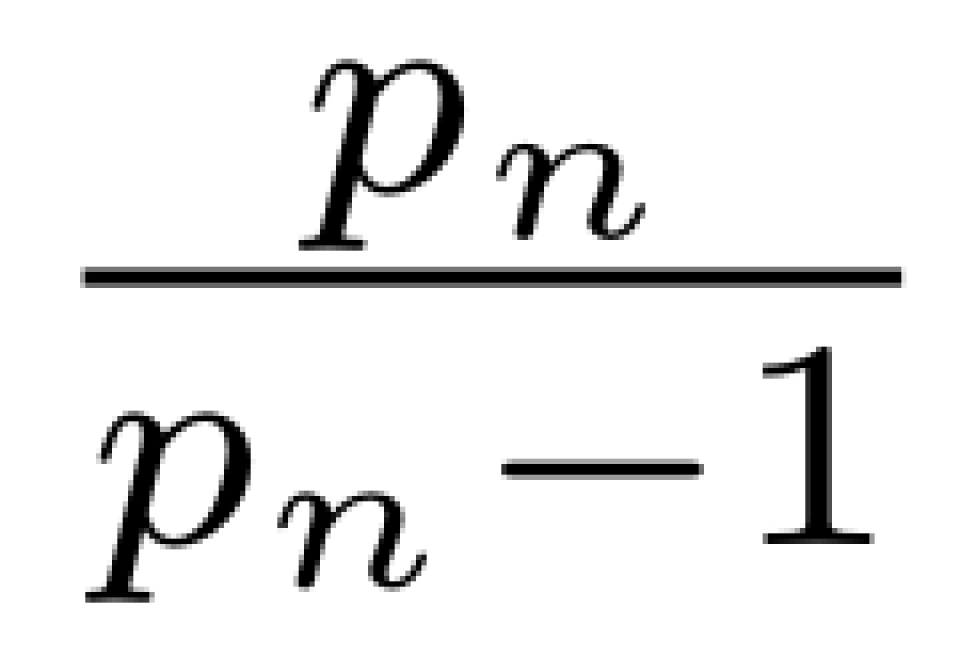
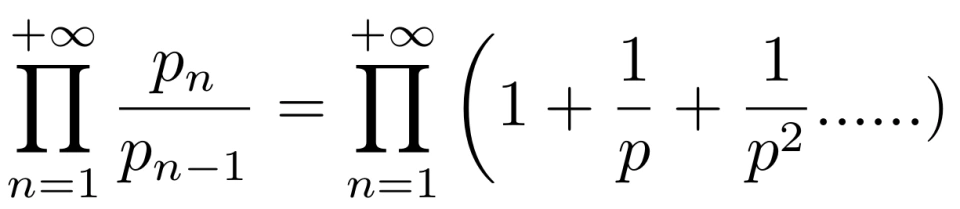
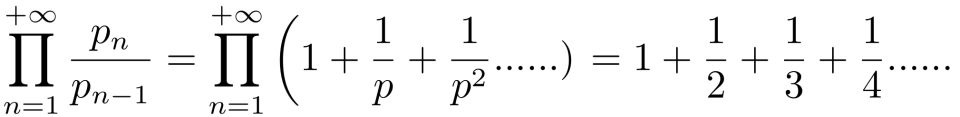
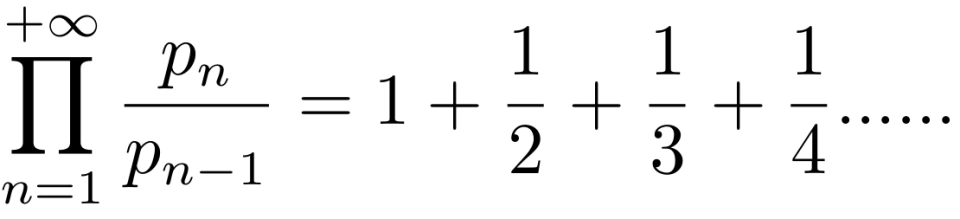
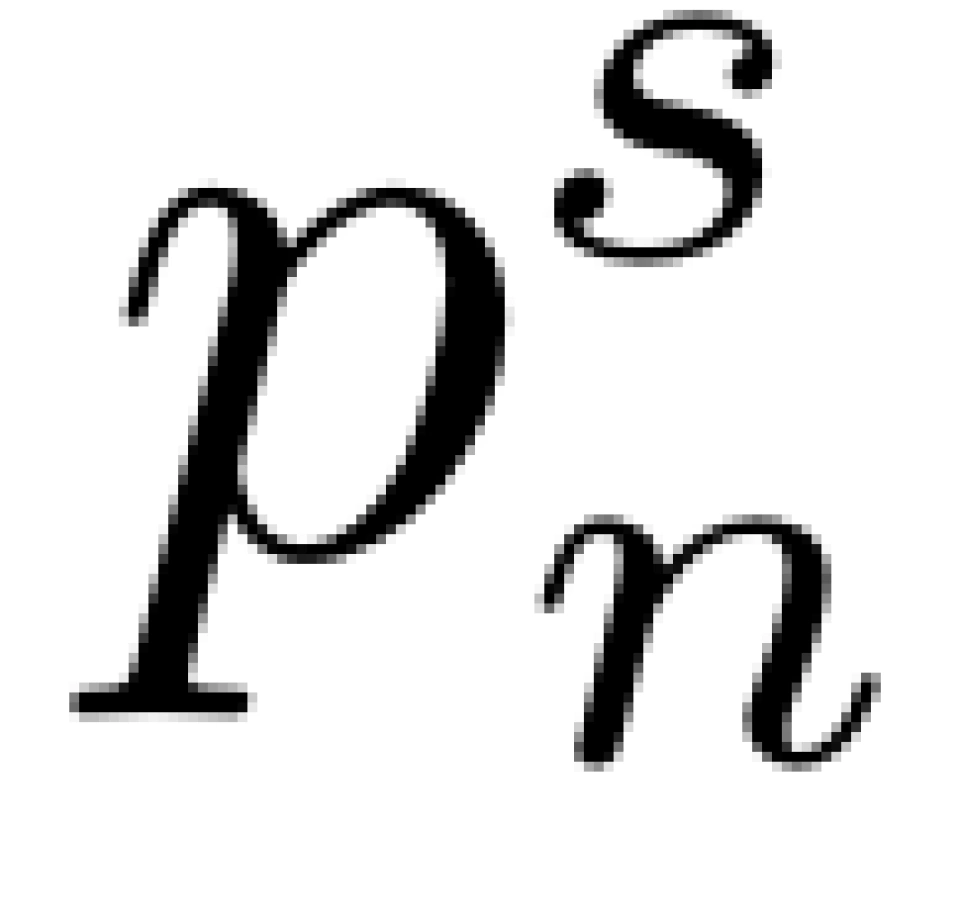
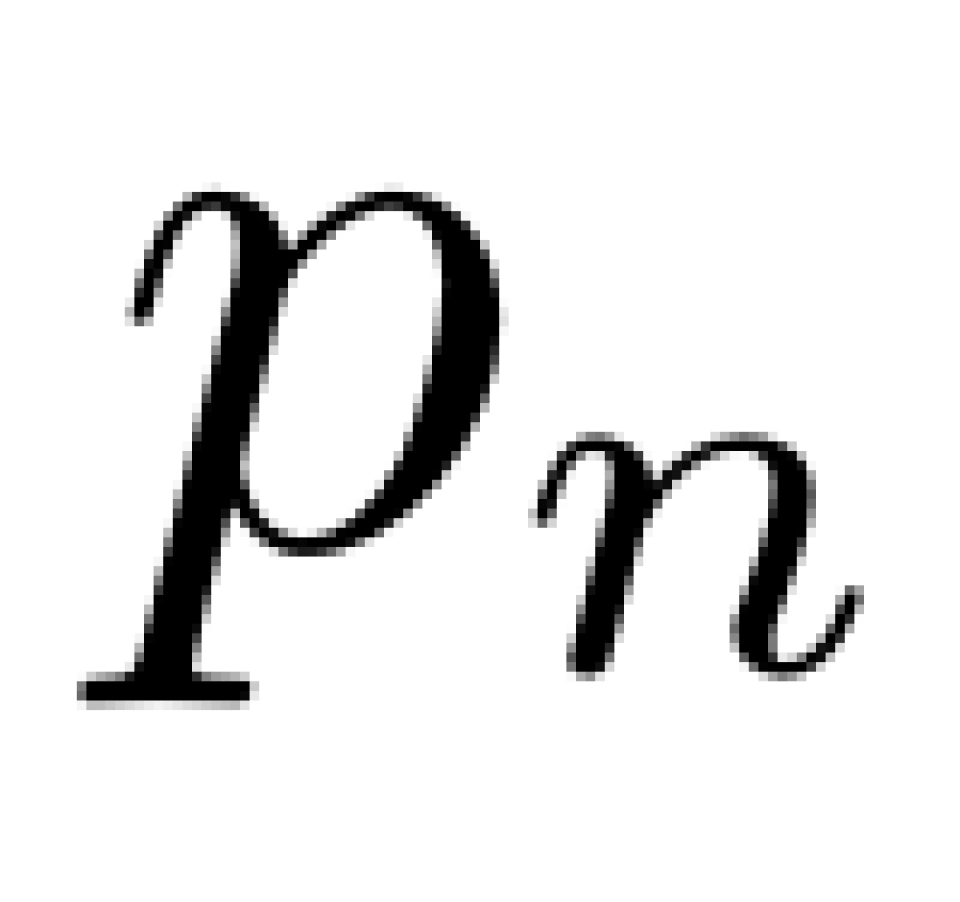
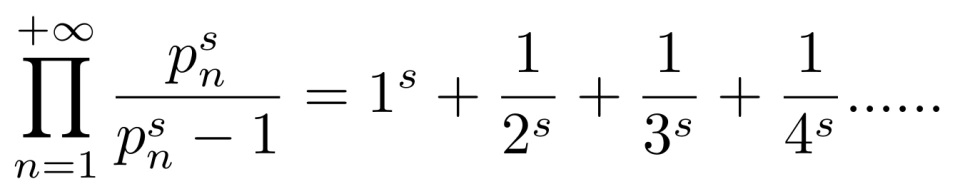
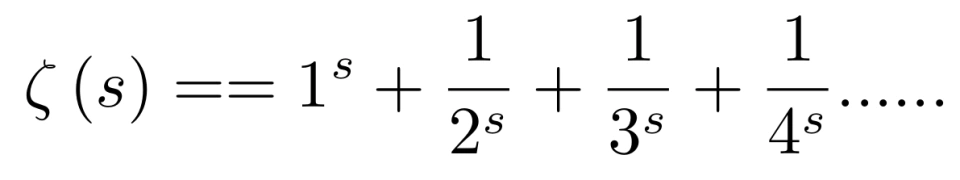
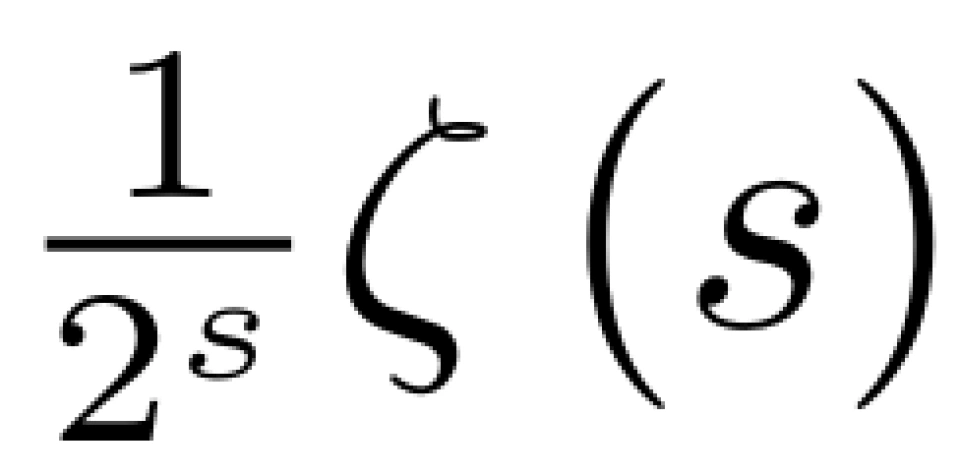
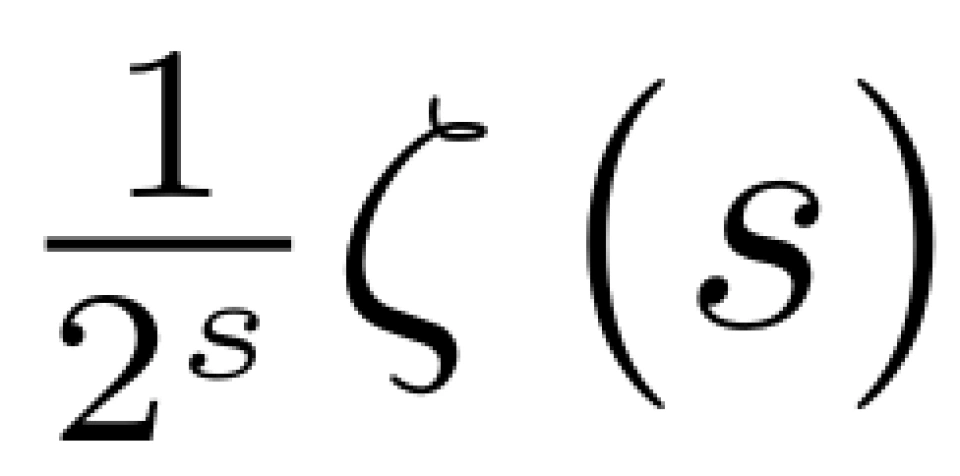
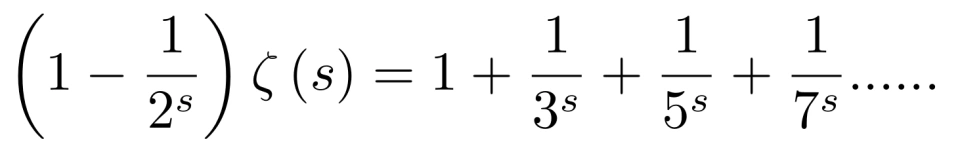
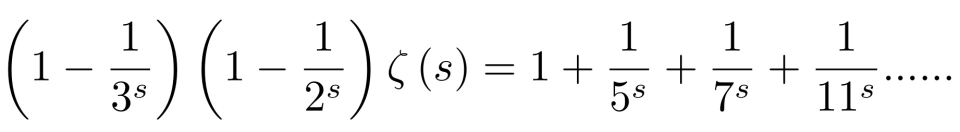
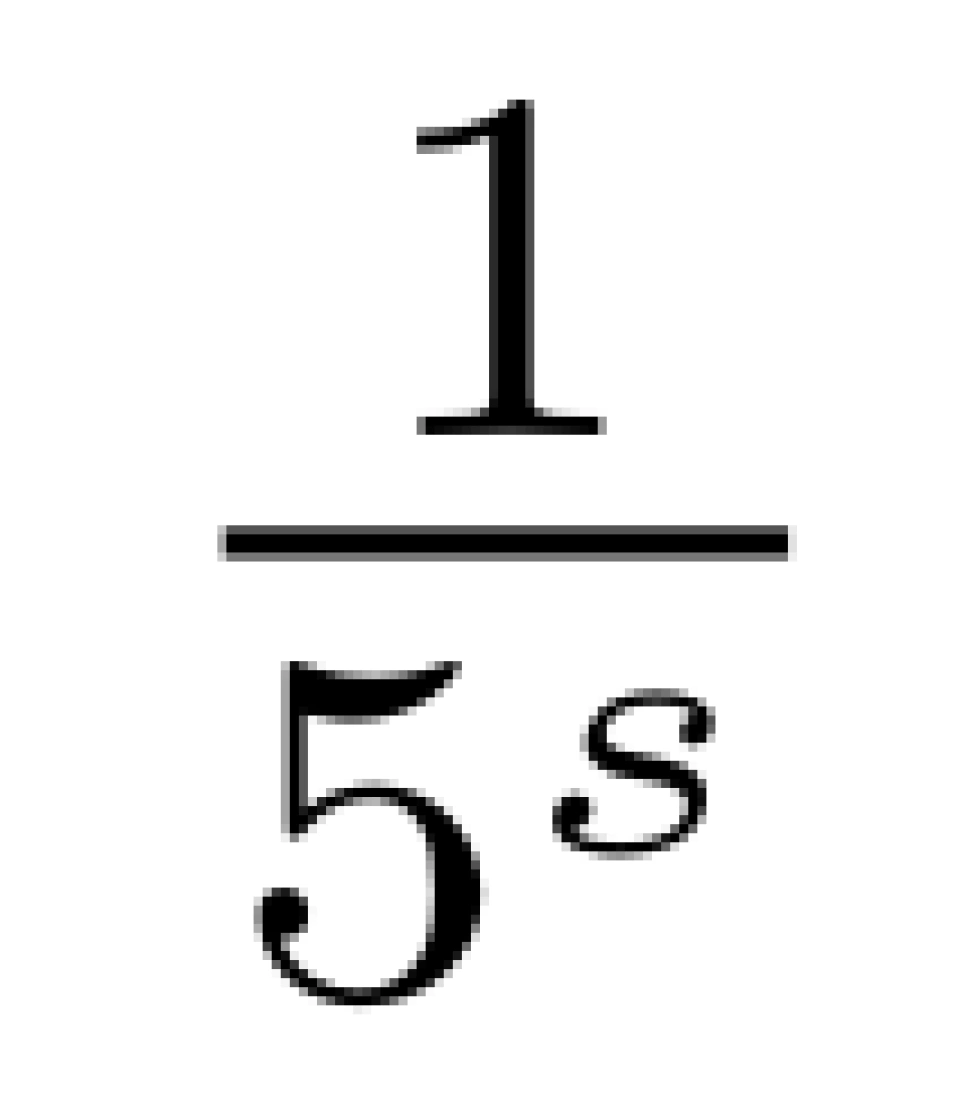
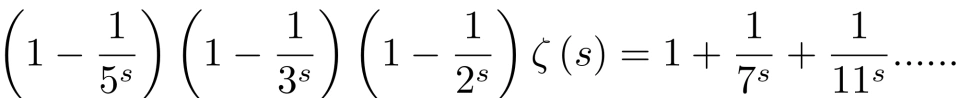
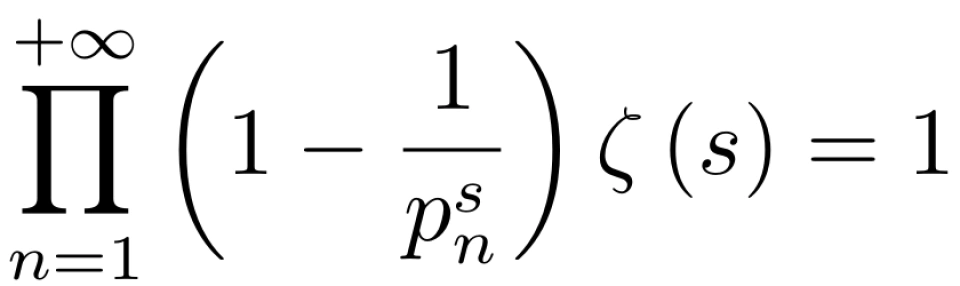
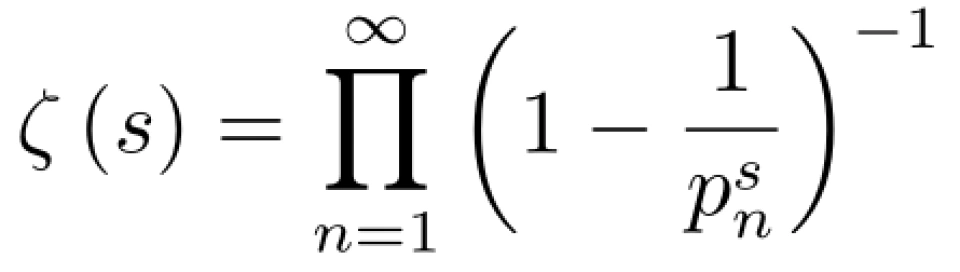
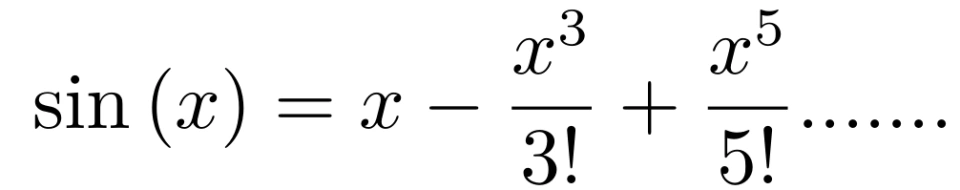
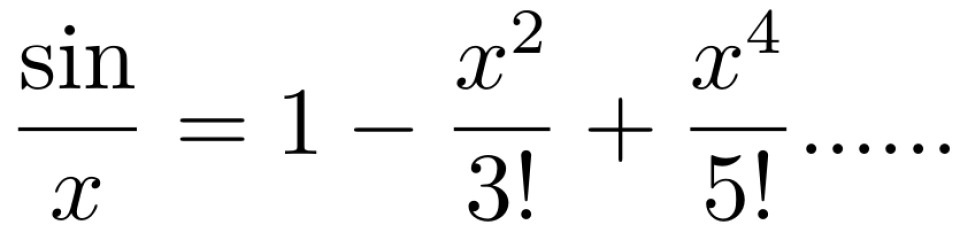
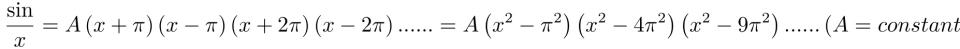
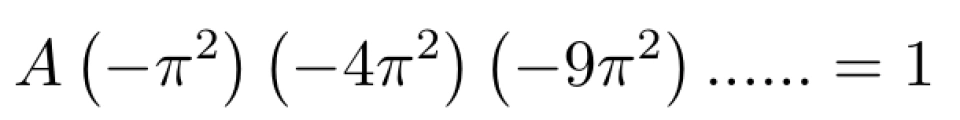
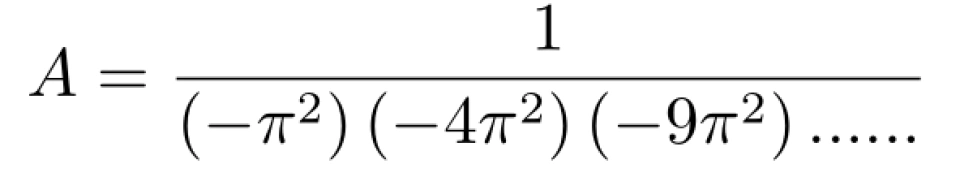
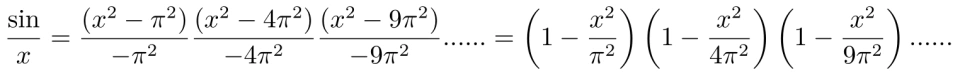
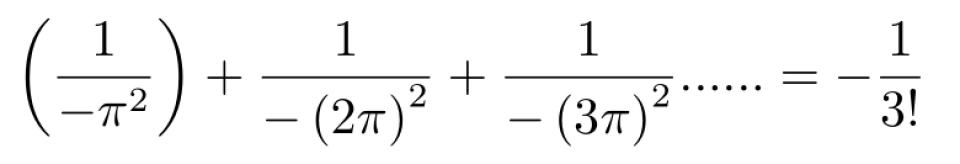
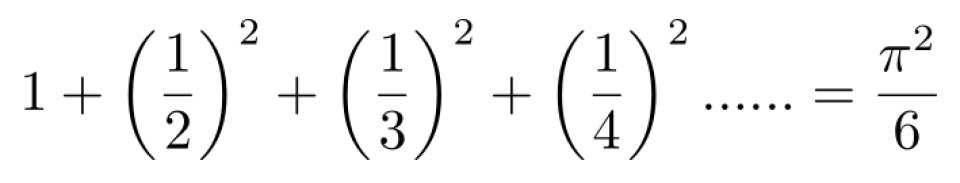
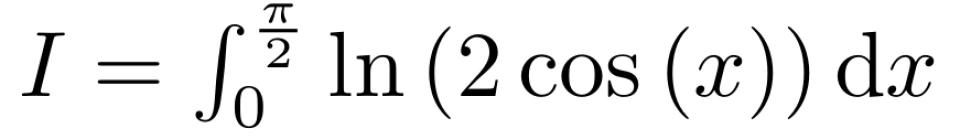
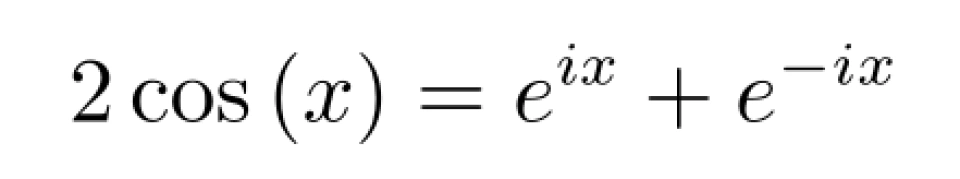
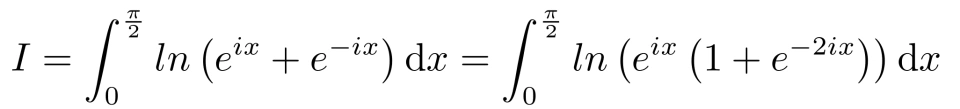
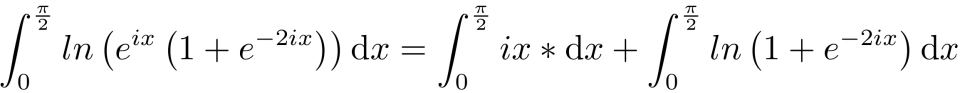
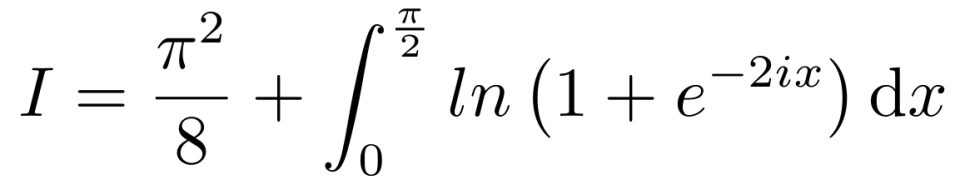
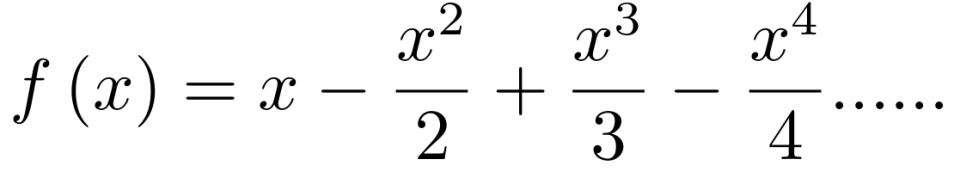
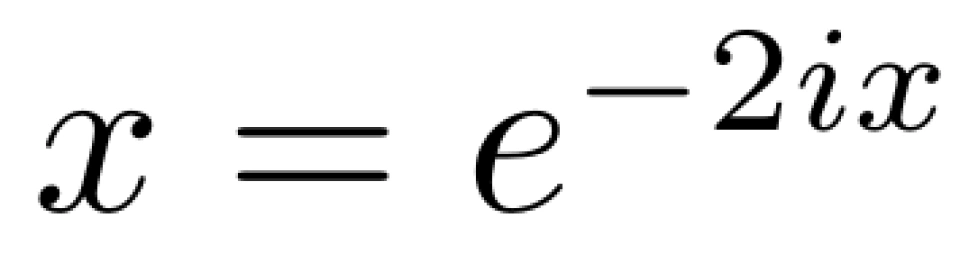
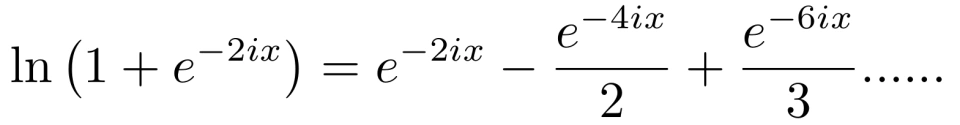
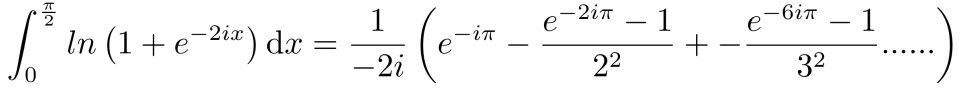
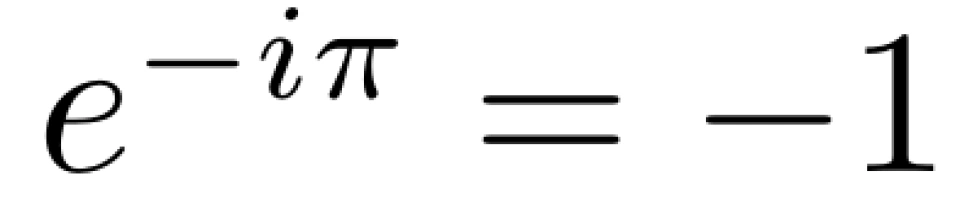
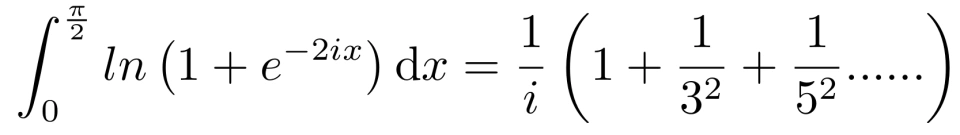
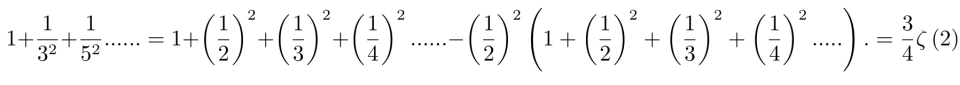
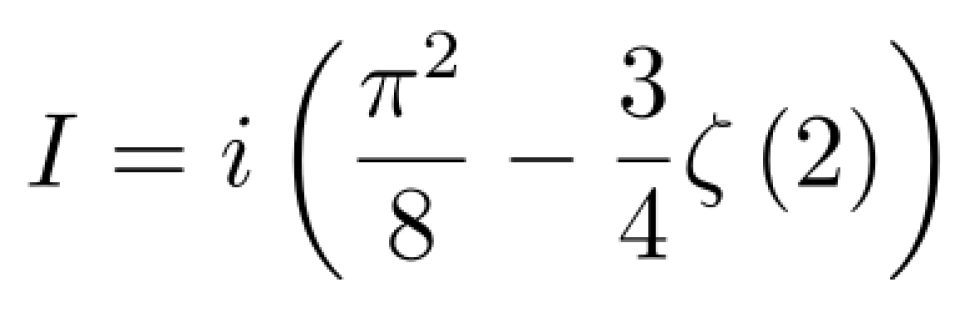
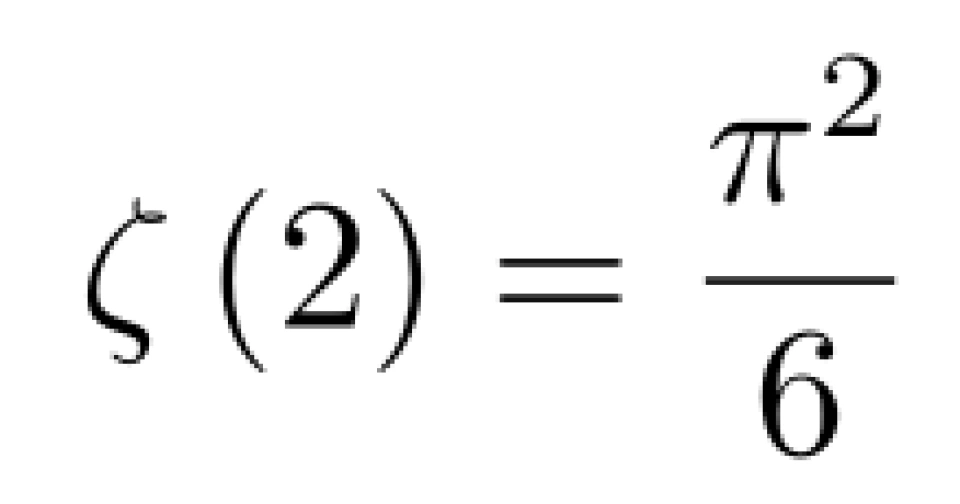
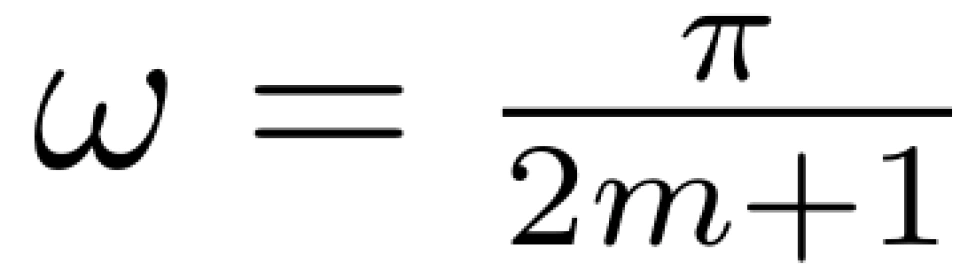
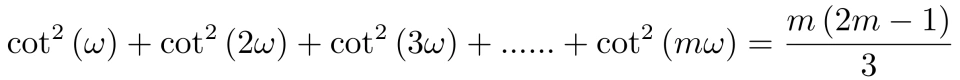
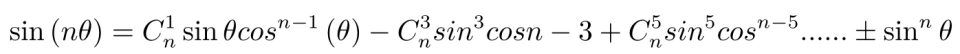
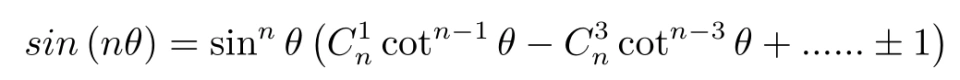
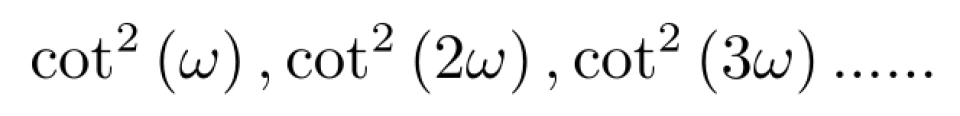
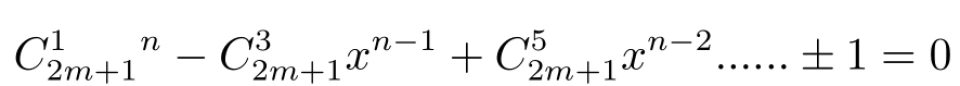
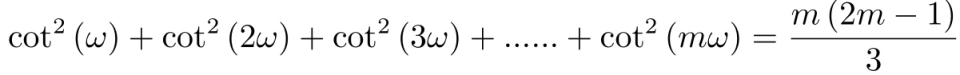
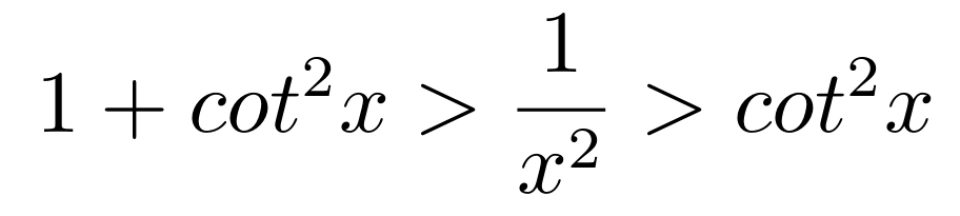
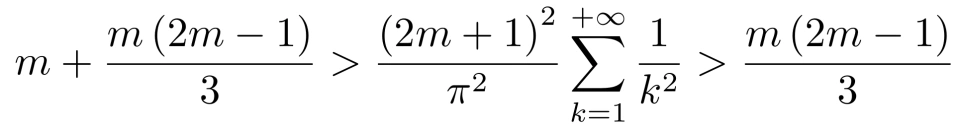
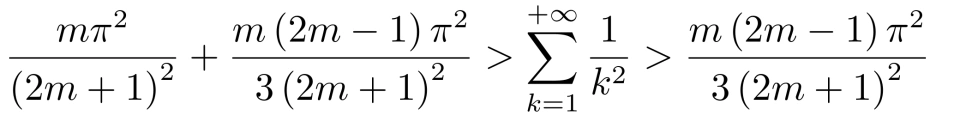
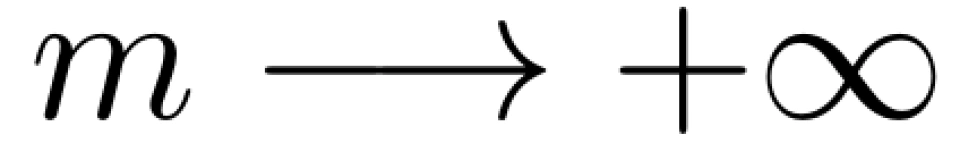
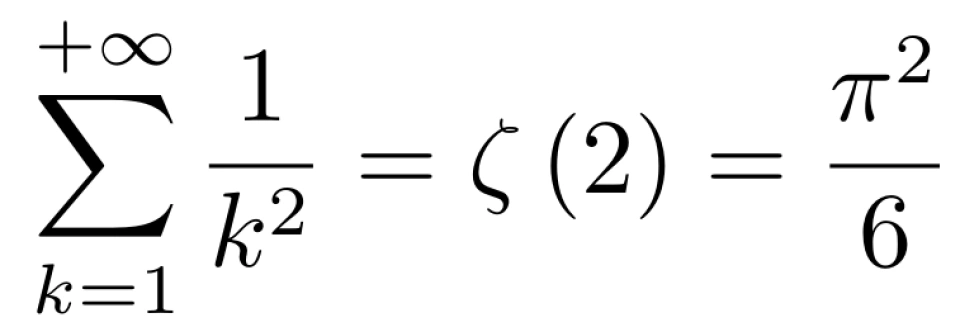
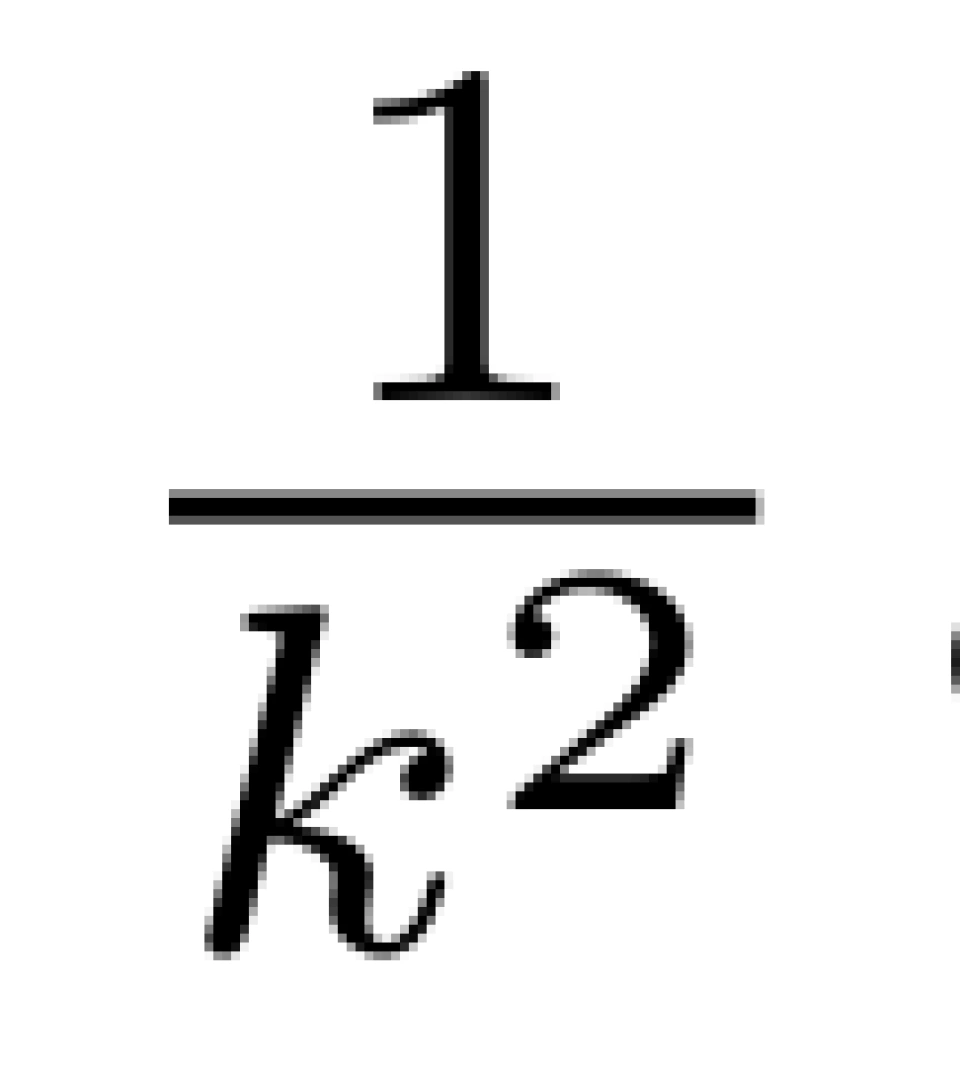
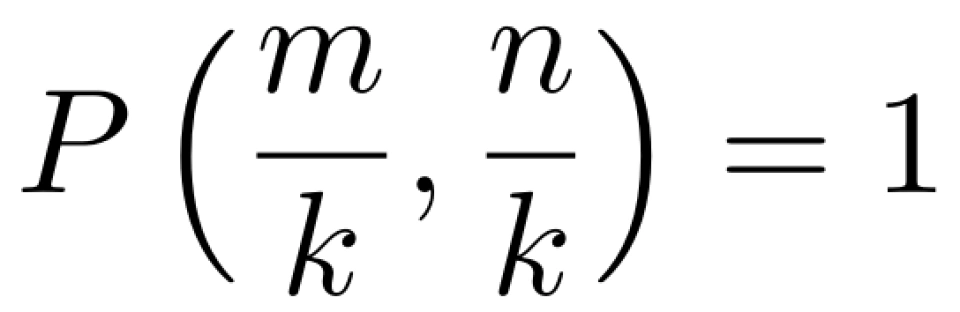
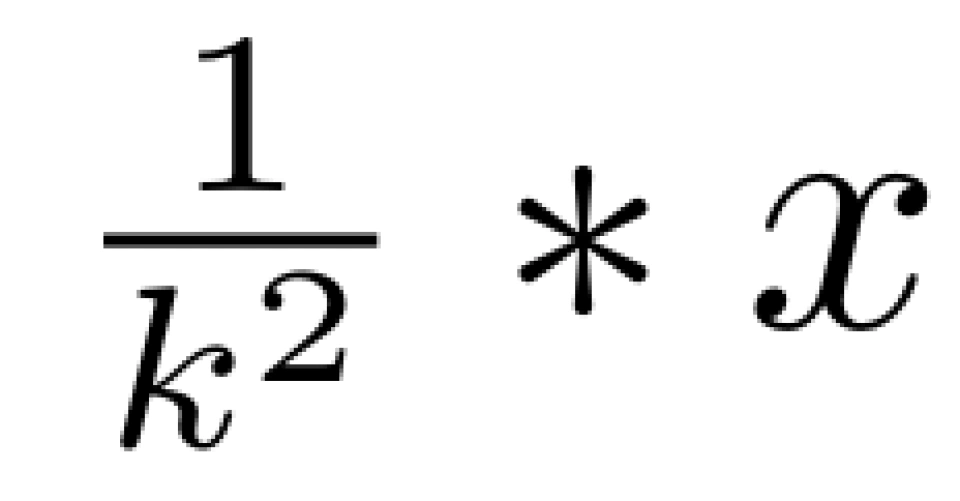
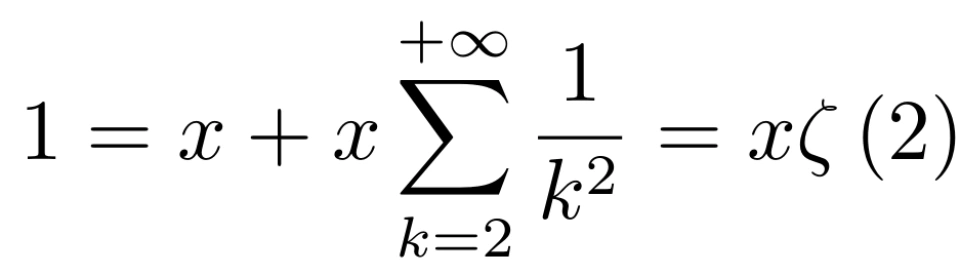
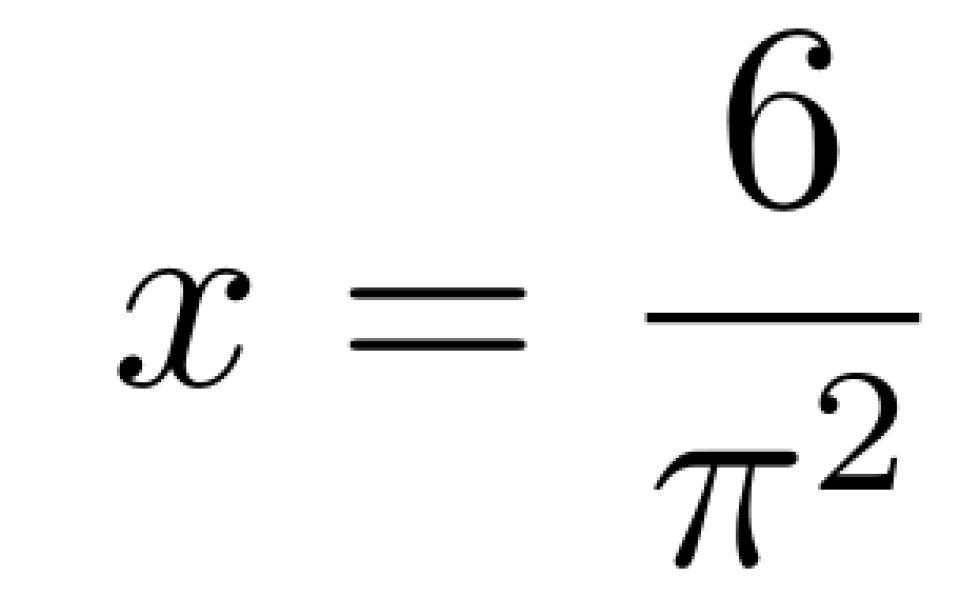













如果读者对文章中的内容有问题,或是对文章排版,语言有意见的欢迎在评论区提出。笔者会尽力的解答,改正。谢谢!![[s-28]](https://www.bokeyuan.net/pic/image/emoji/cas/28.png)
奖励金币:10
奖励理由:内容丰富饱满