第一类方法:实验方法。
这类方法有一个优点和一个缺点。
优点:使用这种方法几乎不需要智商。
缺点:精度实在太低,并且误差不可控。
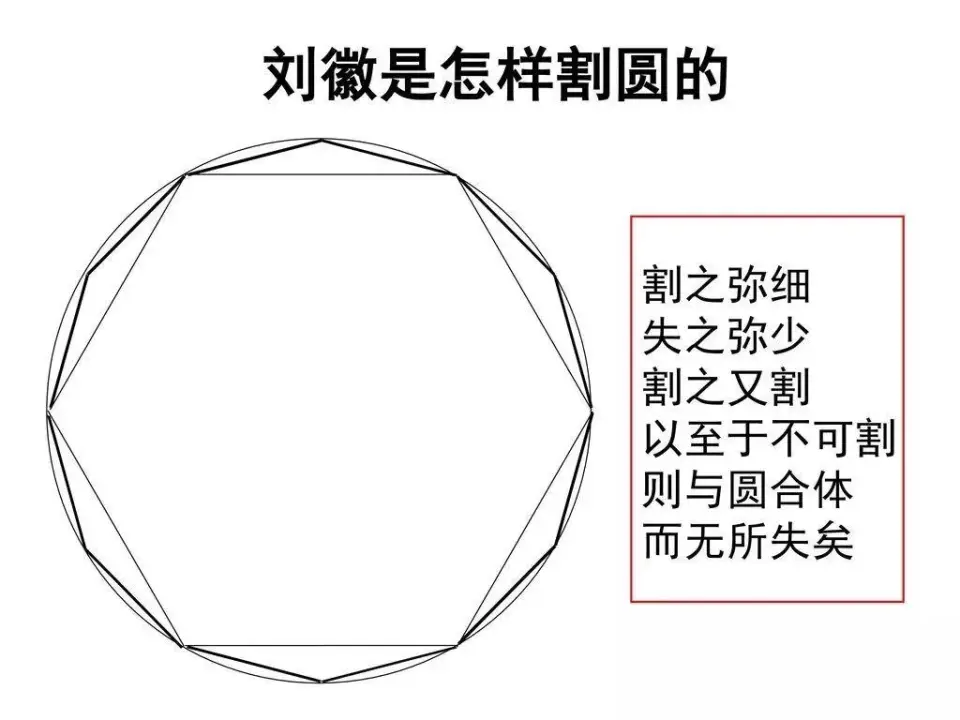
第二类方法:几何方法。
数学正在发展,人们对几何的认识也越来越深,于是人们开始从数学理论上去计算,摆脱了实验方法所带来的机械误差。
这种方法也有一个优点和一个缺点。
优点:可以确定圆周率所在区间,即误差可控,并且不需要做实验,完全没有机械误差。
缺点:几何方法需要频繁地对多位数进行开方,没有机械误差但是有计算误差。
第三类方法:分析方法。
从17世纪开始,人计算圆周率便开始使用无穷积、无穷和、无穷连分等各种无穷表达式。虽然计算误差无法避免,但是此类计算方法可以带到800多位圆周率。例如泰勒级数:
从而得到了
当然,这个式子收敛的极其慢,并不适合计算圆周率,这里仅仅是做理论来说明。
可能有人会问,有没有可以快速收敛的式子,当然有,不过收敛的越快,这个式子就越复杂,例如拉马努金的式子(如下)
或许你觉得拉马努金的式子已经很复杂了,那么请看下面这个式子
这个公式(Chudnovsky公式)曾经用来破计算圆周率精度的世界纪录,每算一项得到14个有效数字,是最快的计算 的无穷级数公式之一。
最后我们在欣赏一下拉马努金其他的充满克鲁苏风格的公式
包含级数形式:
包含积分形式:
包含连分形式:
关于这些定理哈代后来写道:使我束手无策。我连稍微有点像它的任何东西都从未见过。只需看一下它们,就知道它们只能是出自最高级的数学家之手。”
然后,哈代又以自己特有的激动心情继续写道:“它们一定是正确的。如果不正确,谁也不会有这样高的想像力去想出它们。”


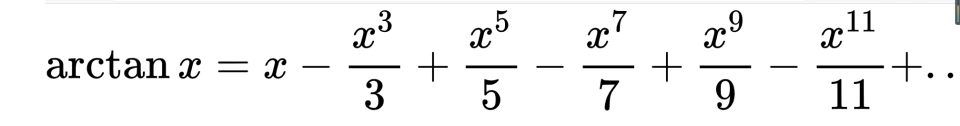
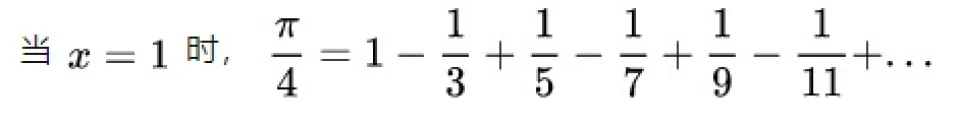
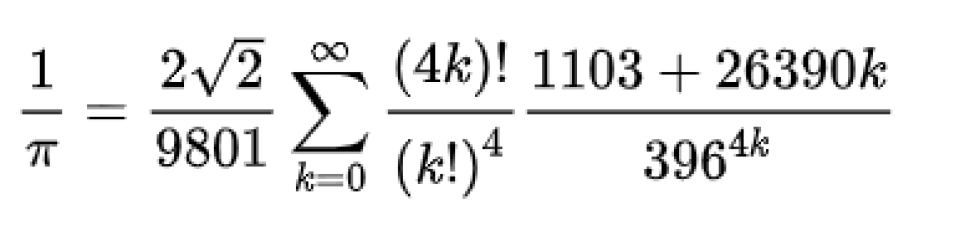
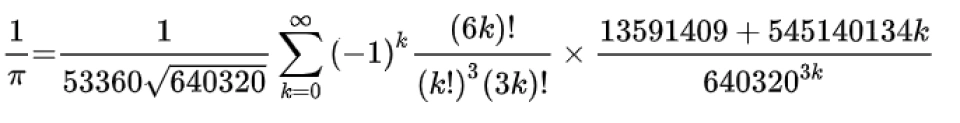
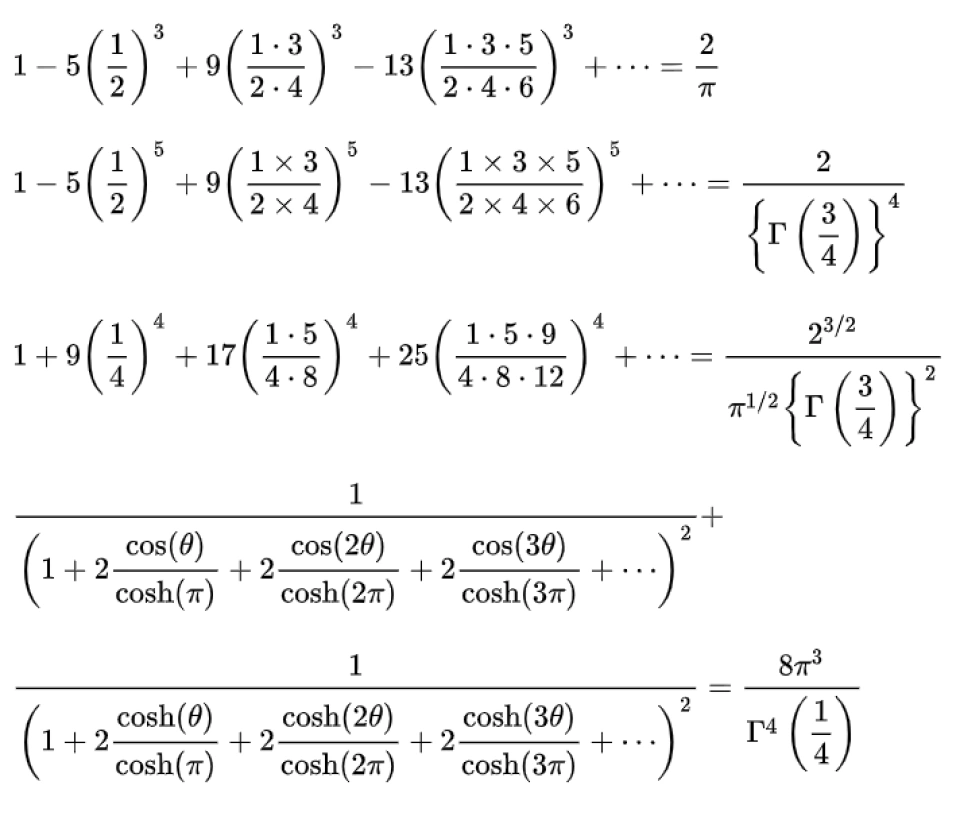




![[s-2]](https://www.bokeyuan.net/pic/image/emoji/cas/2.png)
![[s-5]](https://www.bokeyuan.net/pic/image/emoji/cas/5.png)
![[s-16]](https://www.bokeyuan.net/pic/image/emoji/cas/16.png)












