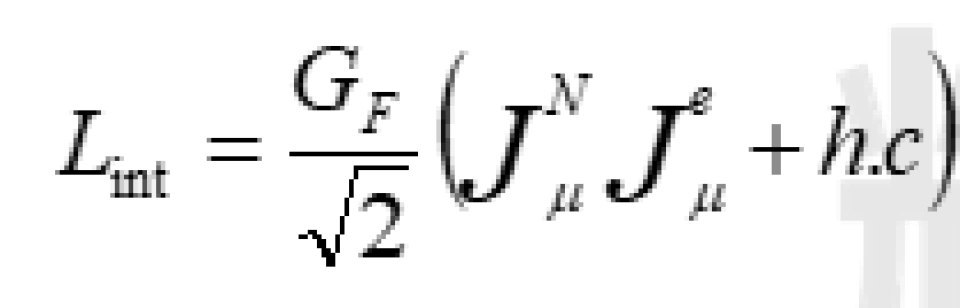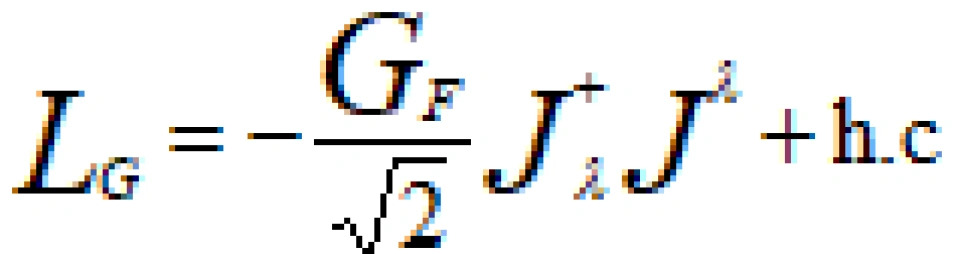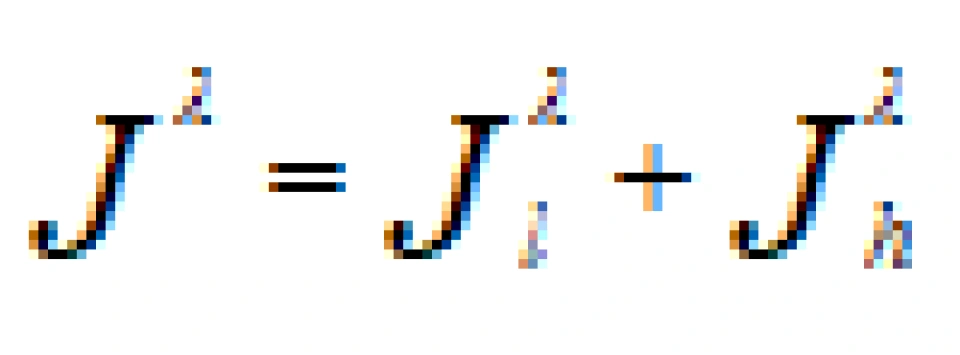科普驿站 第二十八期
主题：粒子物理标准模型
科目：物理
难度：B2
时间：2019.11.9
讲师：弦轴子
标准模型这一章呢，为了能够让大部分朋友理解，我主要讲讲标准模型的发展史。希望用更简洁的语言和例子，能够让你们理解这看似深奥难懂的东西。
这次我要讲的是标准模型。我将把它分成三个部分来讲，分别是：前标准模型时代、标准模型时代以及后标准模型时代。
前标准模型时代:
现在我们就开始讲一下前标准模型时代的事情，也就是标准模型建立之前，人们对于微观世界的探索所面临的情况。关于前标准模型时代，我会从二十世纪四五十年代到标准模型的建立这段时间开始讲起。
首先我们谈一下40年代末建立起来的量子电动力学（QED），堪称有史以来人类所建立的最最精准的量子场理论。可想而知，它的成功给人们带来很多鼓舞。因此，粒子物理学辉煌过一段时间。电磁相互作用的量子场化的完美成功，让人们燃起了希望，也很自然地期望利用类似的方法，能将其他三种相互作用成功的量子场化。
于是有一批人满怀信心地去做这项工作。结果……最后怀疑人生。这也很快导致了粒子物理学整个领域完全崩盘。
人们发现了弱相互作用，并且有人提出描述这种相互作用的理论。这种理论的地位呢，大概就相当于描述强相互作用的汤川的介子理论。
描述弱相互作用的理论被称为四费米子理论（四个费米子点作用）。
那么我来简单谈一谈这个理论所讲的东西。
在泡利提出中微子假说之后，费米呢，又干了一件事。他根据中子衰变（贝塔衰变）：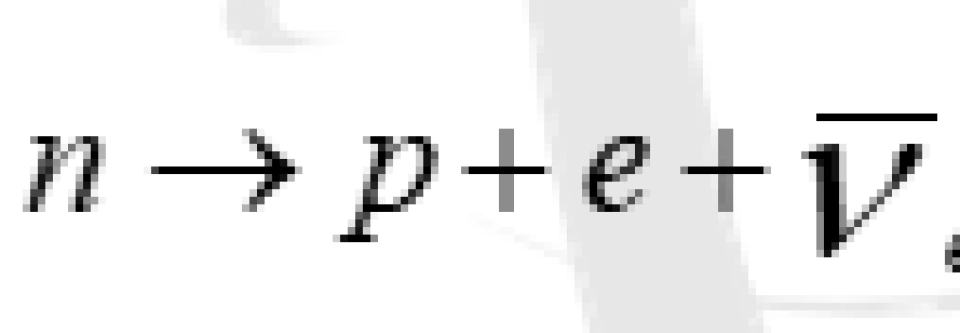
，仿照量子电动力学写出了一个拉氏量：
其中，G＿F是费米耦合常数，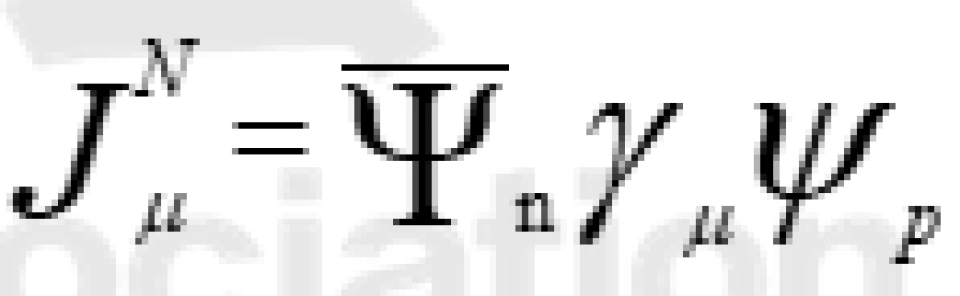
为强子流，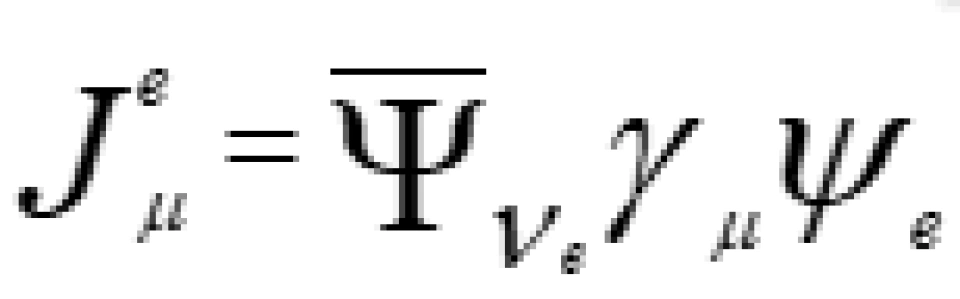
为轻子流，它们都是矢量流（V）。
这个和电磁相互作用流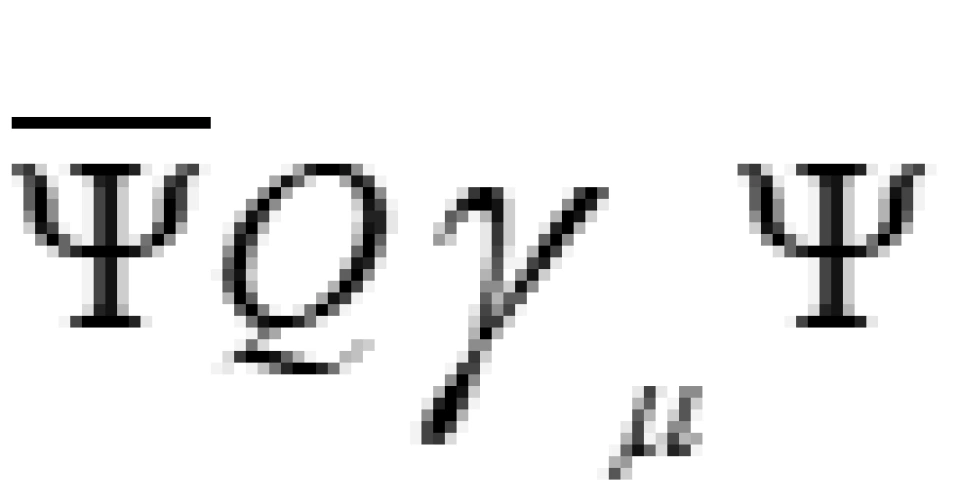
非常相似，那是因为费米也把它当做两种带电流作用，也就是所谓的流—流。
我相信很多人一定听说过，物理学家，最喜欢构造一个拉格朗日量。因为知道一个物理体系的拉格朗日量就可以基本上知道它的所有信息了。但是在粒子物理学中，构造这样的东西呢，必须要结合实验。
随后人们通过实验发现，其他的一些粒子衰变也有类似的形式。也有类似的耦合常数。后来，人们发现费米这个理论不符合伽莫夫——泰勒型β衰变。于是在1936年，伽莫夫与泰勒扩展了费米的理论，引入了轴矢量流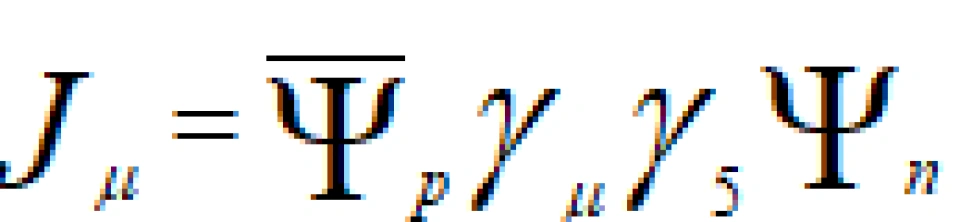
重新改写了上面的拉格朗日量。
到了1949年，三位物理学家（约翰·惠勒，提奥诺·李·罗森布鲁森，杨)提议，为了保障费米理论的普适性，应该对不同的弱相互作用过程都采用同一个耦合常数也就是费米耦合常数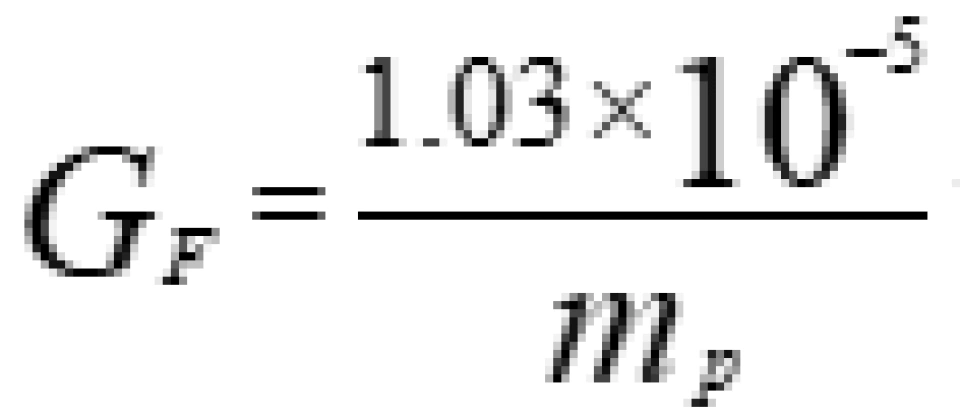
来描述。
著名的宇称不守恒原理——1958年，费曼与盖尔曼、马尔萨克与苏达珊两组理论家几乎同时提出了“V－A”理论，以完善费米理论。这里的V表示中子与质子或中微子与电子形成的矢量流(V)，A代表轴矢量流(A)。带电流－带电流耦合仍然符合先前的理论，只不过现在的流是矢量流与轴矢量流的组合。这里要解释一下，什么叫轴矢量。相信一部分人应该知道“宇称”这个概念，不清楚也没关系，只要把它当作如同电荷、色荷、同位旋、自旋等等那样一种量子数就可以。一般宇称量子数只有两个取值:+1，代表正宇称；-1，代表负宇称。宇称量子数具有乘积性而不是加和性（电荷量子数就具有加和性）。那么我们就把具有自旋量子数为-1、负宇称的物理量称之为矢量，反之称之为轴矢量。
V-A理论的拉格朗日量是:
其中:
，第一个轻子流，第二个就是强子流。
总之无论是四费米子理论还是V-A理论，它们在低能标的情况下，却能很好地描述弱相互作用。只可惜，都是不可重整化的，这一点从它的耦合常数就可以看出来（它耦合常数的量纲是质量平方的倒数）。而且在能量标度比较高的情况下（大约300Gev，就会破坏幺正性/几率性）。当然，对于后者即在高能情况下，破坏几率性可以把流-流作用想象成交换一种虚粒子，这就类似于在电磁相互作用中的流-流交换虚光子一样。这样就可以解决这个高能标下的几率性被破坏的问题，这个假设是由李政道，杨振宁，还有Rosenbluth提出来的。但是这依然是不可重整化的。
那么我们来简单说一下重整化是什么？
简单点来说，重整化的中心思想，是把不需要的无穷大用非物理量的无穷大抵消，使得剩下的真正的可测量的物理量保持为合理的有限值。不可重整的理论则意味着它的发散项有无穷多个，没办法用有限个参量去抵消，这样的理论推广至高能标的时候将会失效。或者讲你要引入无穷多个参数，这显然是不明智的，因为这样会降低理论的价值。当然这是前期人们的看法，现在人们的看法是：理论并不一定需要可重整化，这是威尔逊有效场论的观点。
因此，物理学家们发现弱相互作用的四费米子理论中的无穷大无法用量子电动力学中的重整化方法来消除，这也就意味着，我们无法解决这个问题。也宣告着，我们一开始的假设有可能要被推翻了。不过幸运的是描述强相互作用的汤川介子理论确实是可以重整化的，但是悲惨的是，它是不能用微扰理论的，因为此时相互作用将会变得很强，任何计算都会变成毫无意义的东西。而我们最擅长的就是微扰大法，除此之外我们几乎什么都不会了……
由于理论家们并不能直接求解相互作用方程，只能求解自由场方程，因此在具体求解相互作用方程时，就把相互作用看成一种对自由场的微弱的扰动，把与实验相关的散射截面和衰变宽度等物理量表示成是相互作用强度α的幂级数，然后做级数展开。对于电磁相互作用，由于相互作用强度耦合常数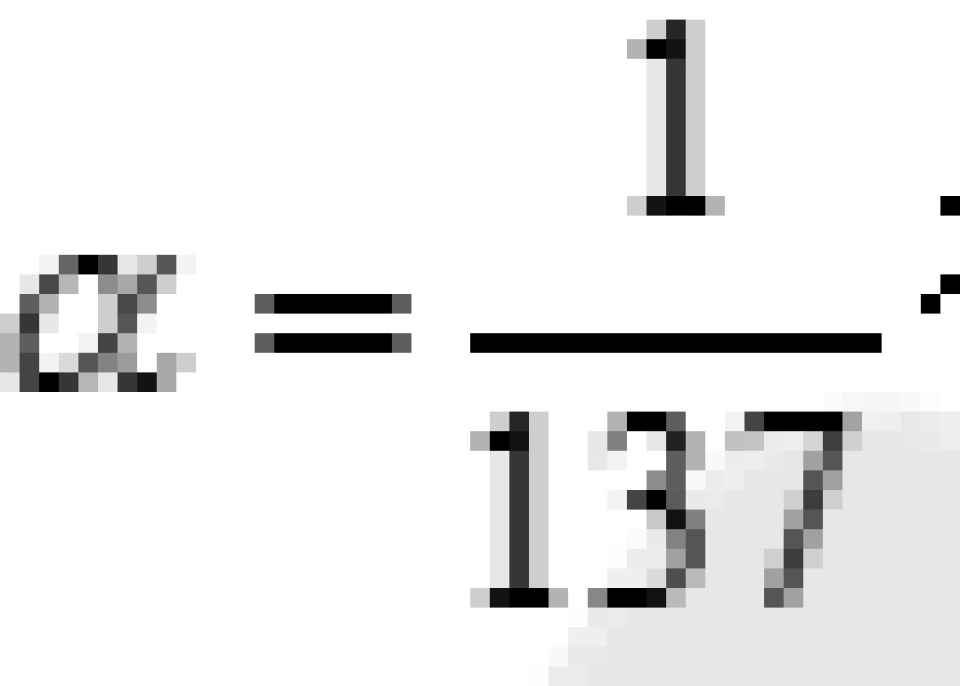
很小，所以就可以逐级求出它的近似解。这种方法称之为微扰论。虽然只是近似但是却能够很好地符合实验。
但是，强相互作用太强了，所以无法用这个方法求解。实验所测定的强相互作用的耦合常数g竟然是15，而不像QED（量子电动力学）中的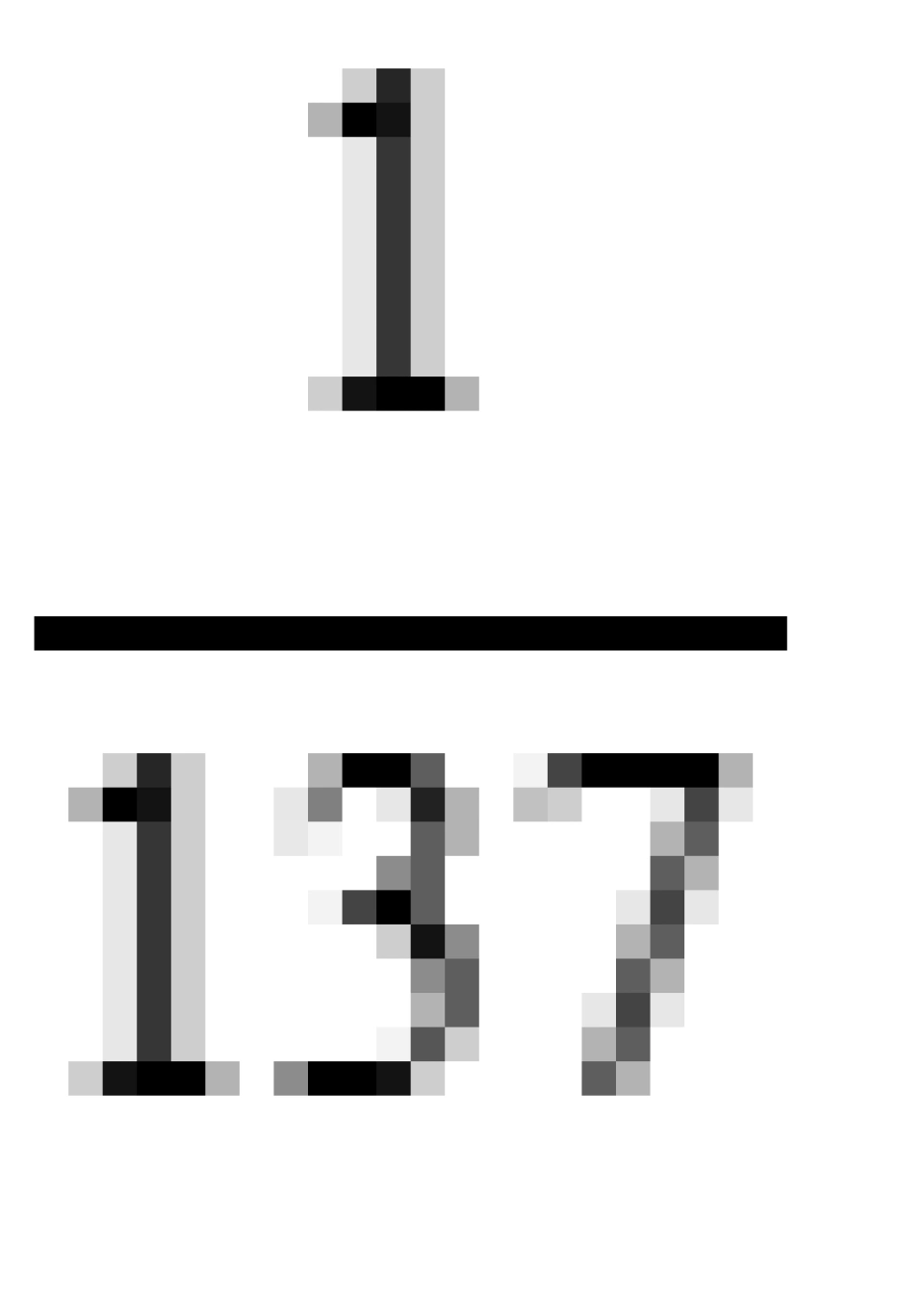
。因此在后续的展开中强相互作用以十五的倍数增长而不是像QED那样以1/137的倍数减小。这样的话，后续无穷多级扰动的幅度变得越来越大，也就不可能去舍弃，也就是说我们不可能主取一阶还能保证与实验符合得很好。
举个例子，（100000000+10.001）^2我们可以近似于（100000000）^2，但是如果是（100000000+1000000）^2呢？后面的小量我们不可能忽略。所以说，你不可能用这种理论来进行定量的预测，因此，不管它是不是可重整化的，整个理论都已经无法做任何有价值的计算了。
就这样，弱相互作用遇到了很大的问题，强相互作用也遇到了很大的问题。一开始的美梦似乎就要终结。所以，当时人们对于量子场论感到很失望，有很多人认为量子场论当时是个过时的理论。
于是，有很多人建立了另一个东西那就是希望最终能为强相互作用构筑一个完全脱离量子场论的纯 S 矩阵理论。但是他们的普遍态度是对于弱相互作用不管不顾，反正交给未来就可以。就这样，五六十年代，理论物理学家经历了很多挫折和不断地艰辛摸索终于得到了三个比较出色的东西；他们分别是夸克模型，（定域）规范对称性，自发对称性破缺。
关于夸克模型我不想多介绍，因为大家基本上都了解而且下文也会涉及到一点。因此，为了节省篇幅，我就不讲了。我主要讲后面两个东西，大家可能会有点陌生。
（定域）规范对称性:
首先,我来说一下为什么称它是定域的，因为与之相对的还有整体连续对称性。我们先不谈这些，先做一下铺垫。简单介绍一下，什么叫规范变换。
规范变换简单点来说就是在内部空间（与之相对的就是时空）的“转动”（加引号是因为这里是数学上的抽象说法）之下，我们对场量作变换。对于这种变换，我们称为规范变换。而内部空间的“转动”，我们用规范群G来表示。然后就有一种叫群参数的东西，它就是变换参数。如果群参数和时空各个点的位置无关，那么时空各点的场就会按照同一个数量变换，我们把这种规范变换称为整体规范变换。相类似就是如果群参数是时空点的函数，那么时空各点的场就会按照各自的数量变化，这种规范变换，我们称为定域规范变换。一般来讲，粒子物理学中的规范对称性指的就是 “定域” 规范对称性。
我们之所以说它是对称性的，是因为我们在规范变换下不改变作用量。可它也不是真正的对称性，因为它（规范变换）不改变可观测量。
之所以会这样，大概是因为，规范对称性只是拉氏量的对称性，而不是体系自身的对称性，而我们通常所讲的一个物理体系有某种对称性只是指它的动力学对称性，通俗点来说，就是它的初态和末态经历一个对称变换。因此，规范对称性就是一个多余的信息。我们压根就不需要它，我们需要的是，可观测的，比如粒子的散射振幅，还有粒子自旋等等……总之，反正只要记住，规范对称性只是拉氏量的对称性，而不是体系自身的对称性就可以了。
那么我们来谈一谈第三个重要的概念–自发对称性破缺。
对称性自发破缺：
对称性自发破缺简单点来讲就是一个物理体系的拉氏量（把它带入欧拉-拉格朗日方程就可以得到该体系的运动方程）具有某种对称性，而基态（体系）却不具有该对称性。换句话说，体系的基态破缺了运动方程所具有的对称性。
让时间回到1954 年，这一年杨振宁和米尔斯建立了Yang-Mills 理论，它是量子电动力学的推广。具体的区别就是它是以非阿贝尔规范对称性亦即SU（2）对称性，取代了量子电动力学所具有的阿贝尔规范对称性亦即 U(1) 规范对称性。
讲到这里，在此之前我们先谈谈U（1）还有SU（2）这些东西到底是什么。
众所周知，如果一个群的表示是N维幺正矩阵，那我们就可以称之为U（N）群。
那么SU（2）呢？我先举个例子:
比如说，我们讲SU（N）群，其实它就是N维特殊幺正群的缩写。另外，这里指的特殊，是指它的矩阵行列式值为1，仅此而已。我们都知道，幺正矩阵的行列式值可以是1也可以是-1，但是我们可以加上一个特殊将研究的对象限定为行列值为1的矩阵。
我们下期继续介绍。
【本文为耀星会的原创作品，未经允许，禁止盗用、转载、篡改文章，否则耀星会将追究版权责任。】
更多科普资源和答疑，请加入耀星会科普官方QQ群：433646418
