浅谈向量与线性

博科园AI人工智能助手 图灵

[ AI在线 ] 4.0大模型 AI对话 AI绘画 AI音乐…

hi 人类

在中学时期，我们将将尽量定义为空间中的有向线段，它由方向与模长唯一确定。后来，我们引入坐标系来描述向量，并借此展开向量的内积、外积运算。这时候，向量长的像有序实数对。

可是，事情真的那么简单吗？

我们不妨看看以下的“巧合”：

①

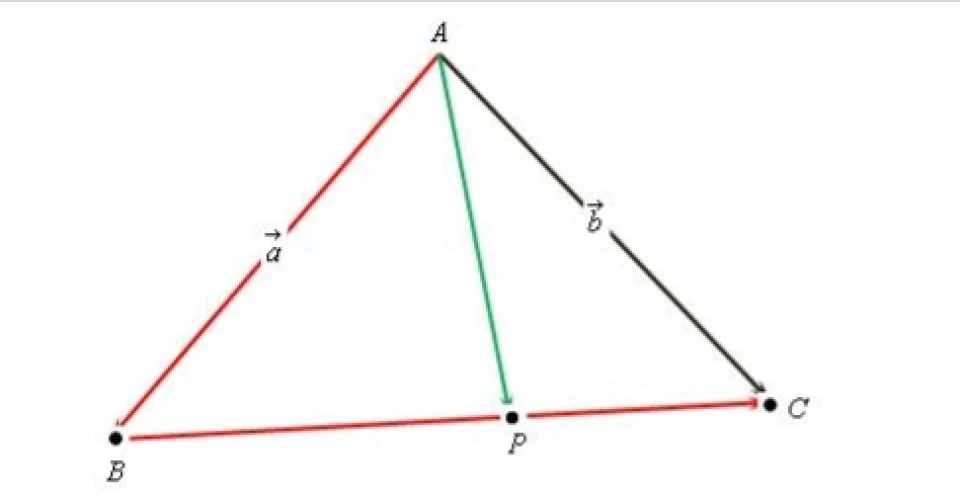
如图，我们知道若B,P,C三点共线且|BP|＝μ,|CP|=λ,则向量AP=（λ∣λ+μ)a+(μ∣λ+μ)b。

同样的情况出现在面积中

如图，若Q、T、P三点共线，且|QT|=λ，|TP|=μ，则S△ABT=（μ∣λ+μ）S△ABQ+（λ∣μ＋λ）S△ABP。

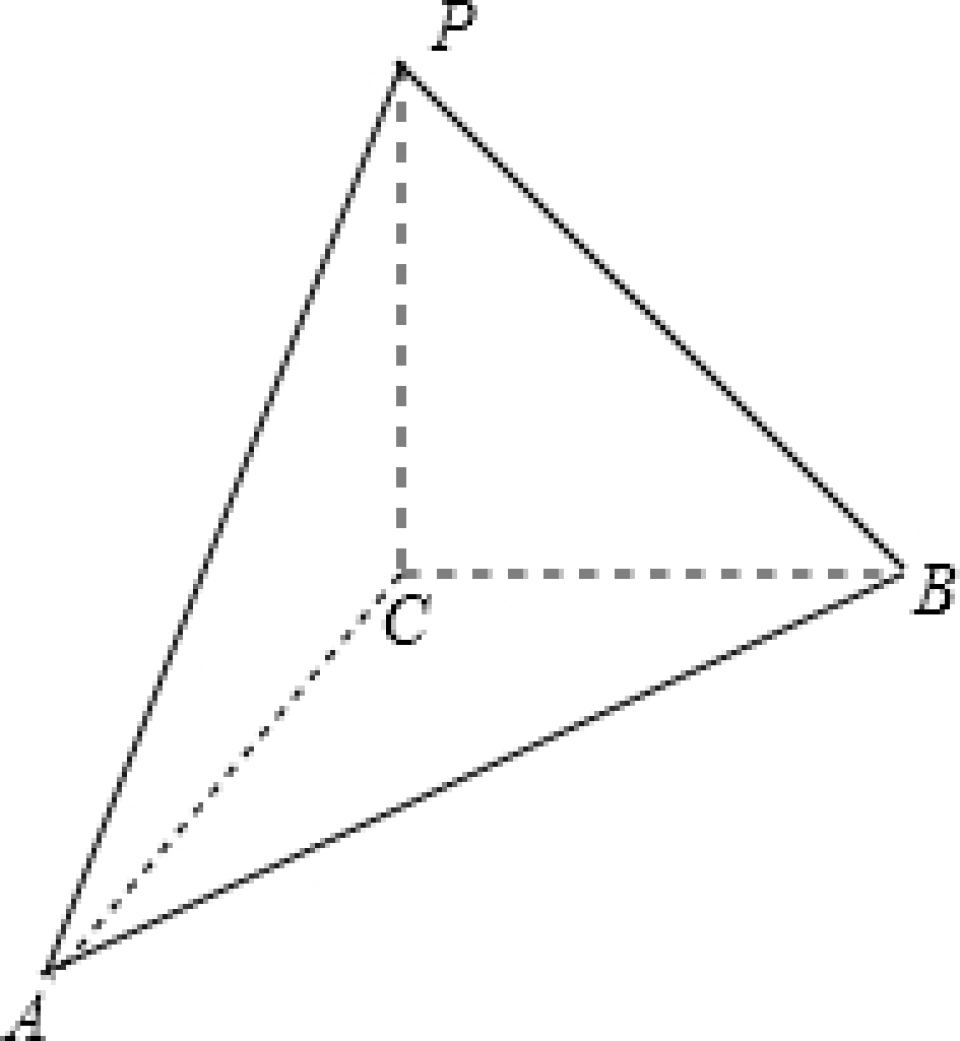
②考虑如下一个直四面体

其中，PC、AC、BC两两垂直，则可以得到S△ABC^2+S△PAC^2+S△PCB^2=S△PAB^2。并且，若定义平面PAB、PAC、PCB、ACB的外法向量分别为c、b、a、p，则有a+b+c+p=0。

③我们在中学学习电通量时知道，有一种计算方法是将所投影平面投影在垂直电场强度的方向上再乘以该平面的面积。

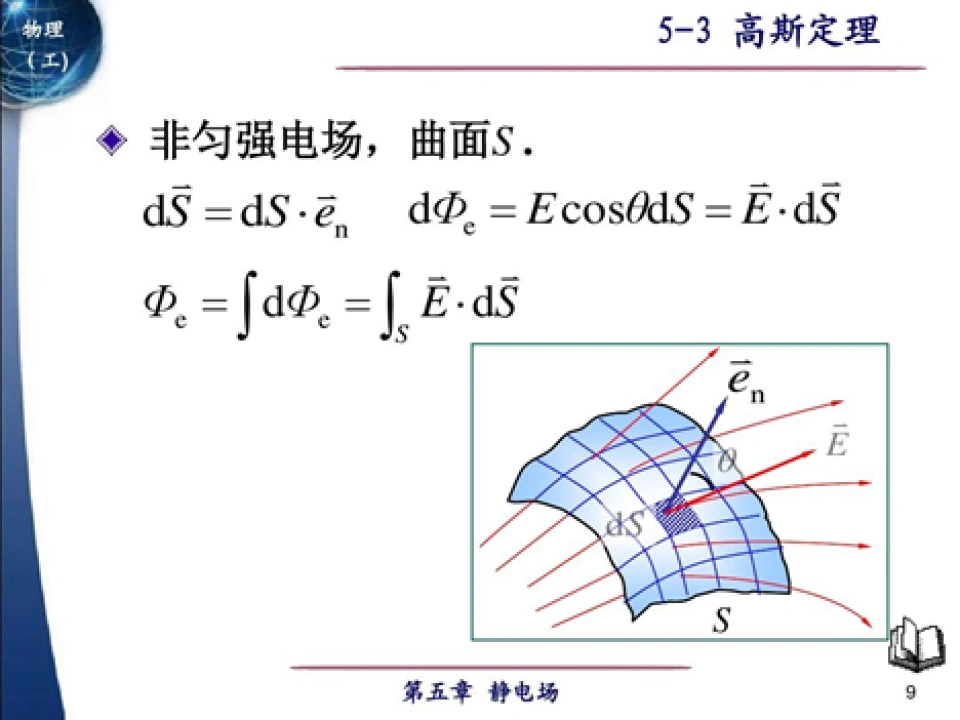
可是，当电通量出现在高斯定理中时，如图所示

面积已然变成了向量。

由以上事实，疑问油然而生：平面，抑或有向面积，究竟是不是向量？

事实上，广义的向量指的是向量空间中的元素。向量空间，又叫线性空间，指的是有线性关系的客体的集合。它的性质如下，在非空集合V和数域P中，V中的元素称为向量，P中的元素称为标量。且

i、在集合V中定义有加法，使所有a，b∈V,都存在a+b=c∈V

ii、在集合V和数域P中，定义有数乘运算，即对于所有u∈V，k∈P，存在运算ku,使得ku∈V

若集合V满足以上条件，则称V为域P上的一个线性空间，或向量空间。

并且，线性空间存在以下8条性质：

1、a+b=b+a

2、(a+b)+c=a+(b+c)

3、1*a=a

4、对所有a∈V，存在（-a）属于V,使得a+(-a)=0

5、0+a=a

6、K(a+b)=ka+kb

7、K(ja)=(kj)a

8、(k+j)a=ka+ja

其中 a、b、c∈V，k、j∈P

到了这里，我们可以给上面的问题做个解答了：广义的向量，指的是一切具有上述线性关系的客体，即线性空间中的元素。它可以函数、有序实数对、有向线段、矩阵等等，也可以是不那么直观的数学客体，如平面等，甚至还可以是其他看似完全与数学不着边际的客体，如苹果、梨等，只要你能定义出这些集合的加法和数乘运算。

下面来谈谈线性变幻（线性映射）的定义：对于域P中的线性空间V和W，若存在映射f：V→W，使得

ⅰ、对任意a∈V,k∈P,都有f（ka）=kf(a)

ⅱ、对任意a,b∈V，都有f（a+b）=f（a）+f(b)

若对于满足以上两个条件的变幻，我们即称为线性变幻。我们熟悉的求导，矩阵，正比例函数等等都属于线性变幻。

放在最后：

笔者只是一名高中生，也是第一次写科普文章，学识有限，能力有限，如文章或其他细节有缺漏，欢迎各位及时指正交流

谢谢！