继开普勒定律发现后,人们开始更深入的思考,是什么原因使行星绕太阳运动?
其实伽利略,开普勒以及笛卡尔都提出过自己的解释,胡克等人认为,行星绕太阳运动是因为收到了太阳对它的引力,甚至证明了如果行星的轨道是圆形的,它所受的引力大小与行星到太阳距离的二次方成正比。
牛顿设想,行星绕太阳运动可以看做匀速圆周运动,行星受到一个指向太阳圆心的引力,正是引力提供了向心力,那么根据引力提供向心力公式F=mv²╱r,再根据天文观测行星公转的周期T,且v=2πr╱T,代入,求出F=4π²mr╱T²
然后根据开普勒第三定律,巧妙的变换一下。(下方图片有推导图)将两次正比联立,得出万有引力定律。其中G值为引力常量,牛顿并未解答出来。大约相继一百年后,卡文迪许利用扭称测量出引力常量G的大小。
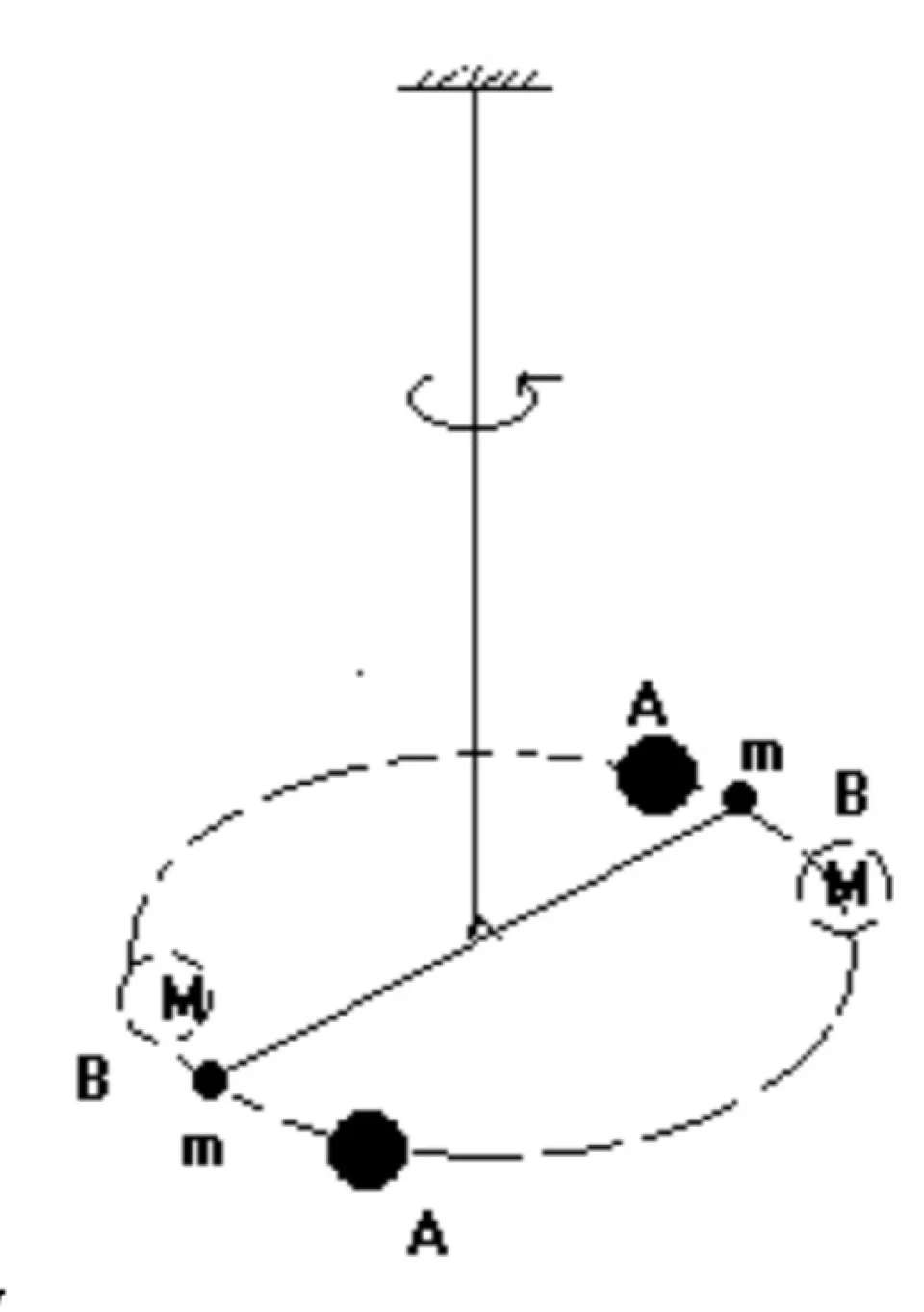
他所用的是扭秤装置,如图所示,两个质量均为m的小球固定在一根轻杆的两端,在用一根石英细丝将这两杆水平的悬挂起来,每个质量为m的小球附近各放置一个质量为M的大球。根据万有引力定律,当大球在位置AA时,由于小球受到吸引力,悬杆因受到一个力矩而转动,使悬丝扭转。引力力矩最后被悬丝的弹性恢复力矩所平衡。悬丝扭转的角度θ可用镜尺系统来测定。为了提高测量的灵敏度,还可以将大球放在位置BB,向相反的方向吸引小球。这样,两次悬杆平衡为止之间的夹角纠正打了一倍。如果已知大球和小球的质量M,m和他们相隔的距离,以及悬丝的扭力稀疏,就可由测得的θ来计算G。卡文迪许测定的万有引力常量值为G=6.754×10-11m3/kg·s2.卡文迪许的实验如此精巧,在八九十年间竟无人超过它的测量精度。万有引力常量是目前测得最不精确的一个基本物理常量,因为引力太弱,又不能屏蔽它的干扰,实验很难做。从卡文迪许到现在已近200年,许多人用相同或不同的方法测量G的数值,不断地改进其精度。国际科学联盟理事会科技数据委员会(CODATA)1986年推荐的数值为 G=6.67259(85)×10-11 m3/kg·s2
万有引力定律发现后,对天文物理学方面产生了巨大的影响,利用万有引力提供向心力,根据一系列的推导,算出恒星的质量,密度(下图)是17世纪最伟大的发现,是人类认识自然界的里程碑! 




![[s-2]](https://www.bokeyuan.net/pic/image/emoji/cas/2.png)











