作者:涛声
文章约5600字,阅读约需要6-8分钟
温馨提示:本篇文章可能需要仔细、分节、多次、反复阅读,请大家做好心理准备。
第一节:引言;
第二节:命题;
第三节:四种直言命题;
第四节:三段论;
第五节:总结。
第一节:引言
在网上冲浪的愉快之旅中,我们总能碰到各式各样的观点:或鞭辟入里,或温暖坚定,或整个好活儿。在这些观点中,我们往往倾向于认同一些观点,否定另一些观点。这不仅能让我们在思考中加深自己对这一问题的理解,构筑自己的观点,也能让我们获得情感支持。
从这一角度看,无论某一观点是在事实、认知或情感等方式是多么不合理或不可接受,它的存在本身就有意义。但这是否能说明,我们可以随意地提出并使用任意观点呢?
让我们来设想这样一种情况:在某一群体中,人们可以自由发表看法,也可以对别人的观点表示赞同或反对,并采取“少数服从多数”的原则进行重大事件决议。这个群体的未来会是怎样的?
由于缺乏判断观点的客观标准,人们之间的沟通交流变成了“巧了,你也是这么想的”的结缘活动,我们不能保证每一个被广泛认同的观点都对群体有益。整个群体的未来就极度的不确定了。那有什么办法能得到一个正确,或者说是在某个角度上是正确的观点呢?
值得庆幸的是,办法总归是有的!只是需要智商。我们需要引入一对概念:“真”与“假”。引入这一对概念后,我们至少在使用观点时拥有了客观判断的工具。
显然,与客观事实不符的观点,我们往往认为它是假的。但有大量的观点是不能通过观察客观事实直接得出的:如,明年今天会下雨。(时间限制导致的无法得知)美国的空气是甜的。(空间限制导致的无法得知)神是存在的。(概念本身难以得知)我们需要大量利用推理来进行论证。
例如,因为空气几乎不可能是甜的,所以美国的空气几乎不可能是甜的。(但在1919年的波士顿北部,空气的确香甜)我们需要一种帮助我们进行判断的艺术,就如同上面的例子一般。
让我们来认识一下推理的艺术吧!还记得我们上文提到的智商吗?现在就要开始使用它了!别担心,毕竟我也没有。
第二节:命题
首先,让我们认识命题。任何一个命题都断定了事情是什么样的。
中国是人口大国。
苹果不脆了。
天在下雨。
这些都是命题。我们可以肯定或否定一个命题,但任何命题都断定了某件事物是什么样的,或者不是什么样的。而这些断定总是与客观事实相符或相悖的,所以每一个命题都要么是真的,要么是假的,不存在既真又假的命题。
当然,有些命题的真假是难以确定的。比如,就我们目前的知识,“有外星人存在”这个命题,它的真假就是未知的。但这个命题和其它命题一样,要么是真的,要么是假的,不可能是既真又假的。
显而易见,问题、命令和感叹虽然都是句子,但都不可能是命题。比如:“看到这里了,你头疼吗?”、“搞快点!”、“我的麻鸭!”都没有断定任何东西,都是非真非假的。
第三节:四种直言命题
紧接着,让我们认识一下四种直言命题。
直言命题也被称作性质命题,是断定对象具有或不具有某种性质的命题。以下几个命题都是直言命题。
②所有狗都不是人。
③有的苹果会被做成Bad Apple!!
直言命题是以主谓式语句表达的,由量项、主项、联项、谓项四个部分组成。
主项是指明断定对象的项。在上面的命题中,“APC联盟”、“狗”、“苹果”、“学生”都是主项。它们通常都长得很像语法概念中的主语。
谓项是描述对象性质的项。在上面的命题中,“很棒的科普组织”、“人”、“被做成Bad Apple!!”、“学形式逻辑”都是谓项。它们通常都长得很像语法概念中的谓语。
联项是联接主项和谓项的词。在上面的命题中,表示“具有”和“不具有”的差别,决定了一个命题是肯定命题还是否定命题。肯定命题的联项通常用“是”这个判断词,否定命题的联项通常用“不是”这个判断词。上文说到,一个命题要么断定了事物具有某种性质,是肯定的;要么断定了事物不具有某种性质,是否定的。所以每个命题都有联项,而且联项必须是要么肯定的,要么否定的,不能既肯定又否定。在上面的命题中,①和③中含有肯定的联项“是”,②和④中含有否定的联项“不是”。
量项是表示主项被断定的范围的项。主项的范围被全部断定的量项叫全称量项,通常用“所有”、“全部”、“任何一个”等表示。全称量项可以被省略,比如将命题②表述为“狗不是人”也说得通。主项的范围被部分断定的量项叫特称量项,也叫存在量项,通常用“有的”、“部分”、“其中一些”等来表示。需要注意的是,特称量项不可以省略。命题③和④中的“有的”绝对不能被删去,否则就改变了命题的含义。含有全称量项的命题被称为全称命题,含有特称量项的命题被称为特称命题。在这里要特别明确一点,特称量项“有的”的确切含义应被理解成“至少存在一个”,而不是“有一些而且只有一些”。比如,在命题④中,不喜欢学习逻辑学的学生数量是没有上限的(或者说,这个数量至多可以是全部)。可能全体学生都不喜欢学形式逻辑,但我们仍然可以描述成“有的学生不喜欢学形式逻辑”。命题④并不断定“有的学生不喜欢学形式逻辑”。
了解完量项、主项、联项、谓项,我们很容易地发现:主项和谓项的位置上可以任意填充不同的内容,而量项的位置上只能填“所有”或“有的”,联项的位置上只能填“是”或“否”。所以,我们把主项和谓项称作直言命题的变项,把量项和联项称作直言命题的常项。
所以,为了减少我们死掉的脑细胞,为了让我们更好地研究这些直言命题,我们选择了一些更简单的方式——符号化。
我们发现,两个变项(主项和谓项)的内容往往千变万化,而两个常项(量项和联项)两两配对只有2×2=4种情况。那么,为什么不把量项和联项的不同组合作为我们描述一个直言命题的重点呢?
而且,我们也观察到,任意一个直言命题的形式总是这样的:
(量项)+主项+(联项)+谓项
在任意一个直言命题中,四个部分缺一不可。“()”仅表示在上文叙述的部分情况中,它们可以在日常用语中省略。比如,将日常语句“人都会长大”省略的项补全,就是“所有的人都是会长大的”。
综上,我们用S和P来表示主项和谓项,用A、E、I、O来表示量项和联项之间不同的组合情况。可表示为:
SAP——全称肯定命题(所有……是……)
SEP——全称否定命题(所有……不是……)
SIP——特称肯定命题(有的……是……)
SOP——特称否定命题(有的……不是……)
上文中的命题①、②、③、④刚好分别是SAP、SEP、SIP、SOP的形式。请大家一定要记住它们。
A E I O
A E I O
A E I O
A E I O
(重要的事情要说三遍,所以第四行被删掉了)
好了,大家记住了吗?让我们开启下面的愉快冒险吧!
第四节:三段论
千呼万唤始出来!欢迎来到三段论的世界!
相信大家总能看到这种形式的推理:
Ⅰ.
没有猫猫喜欢吃皮蛋,
有人喜欢吃皮蛋,
——————————
所以,有人不是猫猫。
我们一起来观察这一推理。
在这组直言命题中,有两个直言命题位于分割线上面,有一个直言命题位于分割线下面。由上面两个命题推理出了下面两个命题。有三个词(猫猫、人、皮蛋)出现在这一组直言命题里,分别出现了两次。
我们把这种形式的推理称为直言三段论。它通常由三个直言命题组成:包括两个直言命题作为前提,一个直言命题作为结论。其中,有且只有三个词出现在其中,每个词在其构成命题中恰好出现两次。
要得到更加准确的分析,这样的推理就必须以标准形式出现。(脑容量友好协议)直言三段论的标准形式必须满足以下两个条件:
a. 其前提和结论必须都是标准直言命题(A、E、I、O)
b. 这些命题必须以特殊的顺序出现。(前提——结论,后文会有更详细的补充)
与我们划定直言命题的四个部分(主项、谓项、量项、联项)类似,我们可以对直言三段论的三个词作出命名。以例子中的直言三段论Ⅰ为例,我们发现它包含了三个词:人、猫猫、皮蛋。
要通过名称指认出这三个词,我们一般先观察结论。直言三段论Ⅰ的结论是一个O命题(SOP):“有人不是猫猫。”结论的主项(人)被称为直言三段论的小项,结论的谓项(猫猫)被称为直言三段论的大项。在结论中不出现,而在前提中出现两次的项(皮蛋),即直言三段论的第三个项,被称为中项。
直言三段论的前提也有名称,它们因其中出现的项而得名。大项和小项必须出现在不同的命题中,包含大项的前提被称为大前提。直言三段论Ⅰ中,“猫猫”是大项,所以包含“猫猫”的前提——“没有猫猫喜欢吃皮蛋”——是大前提。
包含小项的前提被称为小前提。直言三段论Ⅰ中,“人”是小项,所以包含“人”的前提——“有人喜欢吃皮蛋”——是小前提。
需要注意的是,这两个命题称为大前提或小前提,并不是因为它们出现的顺序,而是因为它们包含的是大项还是小项。无论这两个前提以何种顺序排列,含大项的前提都是大前提,反之亦然。
如果一个三段论的前提以标准形式排列,就称其为直言三段论的标准形式。还记得上文提到的“直言三段论的标准形式的条件b”吗(希望你不会被绕晕,毕竟下文还有更晕的)?现在我们就来正式描述这个标准顺序:
大前提
小前提
————
结论
在标准式直言三段论中,大前提处在第一位,小前提处在第二位,结论在最后。是的,你没有看错,就是这么简单!请牢牢记住它!
接下来,我们来讨论直言三段论的式与格。(放松下大脑再开始吧,凡人!)
每个直言三段论都有一个式。三段论的式由其所含标准直言命题而定(以A、E、I、O为标志)。每个三段论的式都由三个按特定顺序排列的字母组成。第一个字母指的是大前提的类型,第二个字母指的是小前提的类型,第三个字母指的是结论的类型。如,在直言三段论Ⅰ中,大前提(“没有猫猫喜欢吃皮蛋”)是一个E命题(SEP形式),小前提(“有人喜欢吃皮蛋”)是一个I命题(SIP形式),结论(“有人不是猫猫”)是一个O命题(SOP形式)。所以,这个直言三段论的式就是EIO式的。我们可以列举出4×4×4=64种不同式的直言三段论。
只有式,我们还不能完全刻画标准直言三段论的形式。这一点可以通过比较两个有相同的式的直言三段论表明,它们在逻辑上天差地别。
Ⅱ.
所有飞虫是有翅膀的。
有的鸟是有翅膀的。
——————————
所以,有的鸟是飞虫。
Ⅲ.
所有干饭人是快乐的人。
有的干饭人是学生。
——————————
所以,有的学生是快乐的人。
两者都是AII式,但直言三段论Ⅱ是无效的,直言三段论Ⅲ是有效的。我们如果能展示出它们的“骨架”,就能十分清晰地揭示出其形式上的不同之处。把小项记为S,大项记为P,中项记为M,“所以”记为“∴”,我们得到了这样两个直言三段论的“骨架”:
Ⅱ.
PAM
SIM
————
∴SIP
Ⅲ.
MAP
MIS
————
∴SIP
两者很不同。在直言三段论Ⅱ中,中项在两个前提中都作谓项;在直言三段论Ⅲ中,中项在两个前提中都作主项。直言三段论Ⅲ被视为有效论证,而直言三段论Ⅱ无效。
这个两个例子表明,尽管直言三段论的形式可以部分地用式来描述(两个例子都是AII式),但相同式的直言三段论在形式上还有其它的重要区别,这就需要关注中项的相对位置。为了完整地描述直言三段论的形式,我们不仅需要写出它的式(代表其三个命题的三个字母),还需要写出它的格——中项在前提中的位置。
直言三段论有且只有四种不同的格:
1. 中项在大前提中作主项,在小前提中作谓项;
2. 中项在两个前提中都作谓项;
3. 中项在两个前提中都作主项;
4. 中项在大前提中作谓项,在小前提中作主项。
中项的这些可能组合分别构成了直言三段论的第一、二、三、四格。任何一个直言三段论都有且只有这四种格中的一种。为了便于记忆(请先确认一下自己的大脑温度,避免烧坏),我们将优化这四种格的呈现方式。下面的组合中,只显示了中项的相对位置,而隐藏了它们的式,量项和联项也都没有显示。
M——P
S——M
——————
∴S——P
第一格
(可记为M为一捺)
P——M
S——M
——————
∴S——P
第二格
(可记为M为右竖)
M——P
M——S
——————
∴S——P
第三格
(可记为M为左竖)
P——M
M——S
——————
∴S——P
第四格
(可记为M为一撇)
至此,只要指明标准直言三段论的式与格,就能完整地描述它的形式。我们以直言三段论Ⅰ为例,它属于第二格,因为它的中项“皮蛋”是两个前提的谓项。它的式,则是上文指出的EIO式。所以,这个标准直言三段论应该被完整描述为EIO-2形式。这是一个有效的三段论。
我们在上文中已经计算出,直言三段论会有64种不同的式,而直言三段论又有四种不同的格,所以标准式的直言三段论就必然有64×4=256种形式。
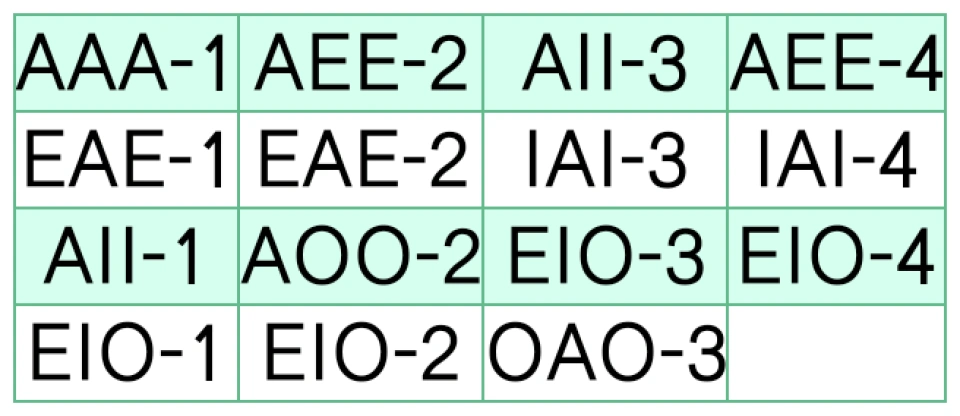
但正如我们所看到的,这其中绝大部分形式是无效的,只有15个形式在任何情况下都有效。
它们分别是:
尤其要牢记的是:只有作前提的两个直言命题都是真的,直言三段论的形式也是有效的,结论才必然是真的。
如,人教版高中语文必修四(实验教科书,即老教材)在《逻辑与语文学习》这一单元中,在介绍推理的时候,将“人非圣贤,孰能无过?”解释为一个省略了的直言三段论,并将它还原为:
Ⅳ.
圣贤是不会有过错的,
我们不是圣贤,
——————————
所以,我们不是不会有过错的(我们都是会出错的)。
其实,这是一个大前提错误且形式无效的三段论。“圣贤是不会有过错的”不符合历史事实和常识——古往今来的任何圣贤都犯过错;这个三段论属于AOO-1形式,形式本身无效。
第五节:总结
我们的传统形式逻辑之旅圆满结束!希望大家以后看到与自己相同或不同的观点后,不再站队,多多运用本文试图阐明的一些基本方法加以判断、思考(而不是站队或对线)。
而这,也正是推理的艺术——证明论证是合理的。
(好了,我要去喝点冰阔乐了,给自己的大脑降降温QAQ)
⭐注:
1. 本文为快进到三段论的有效形式,省略了大量传统形式逻辑的内容。这些重要的内容主要包括:概念(语词)、对当方阵、换质位法、属加种差概念、周延、直言三段论的基本规则、传统解释与布尔解释、标准直言三段论15个有效形式的证明。
2. 本文没有涉及日常用语中的谬误和非形式逻辑情况,读者可自行了解。比较重要的谬误有:诉诸情感、诉诸暴力、红鲱鱼、稻草人、歧义等。
3. 本文部分用词不准确。比如,语词这一概念未被明确。这是因讲解而作出的妥协,读者可自行了解。
4. 现代形式逻辑(数理逻辑)与辩证逻辑未被本文涉及,读者可自行了解。
5. 逻辑作为一种思维工具,不能替代其它学科的重要地位,也不可用于撼动良善的价值观或谋求真理之外的利益。敬请谨记!
作者:涛声
APC科学联盟 科普组
本文未经允许禁止转载或商用




![[s-3]](https://www.bokeyuan.net/pic/image/emoji/cas/3.png)