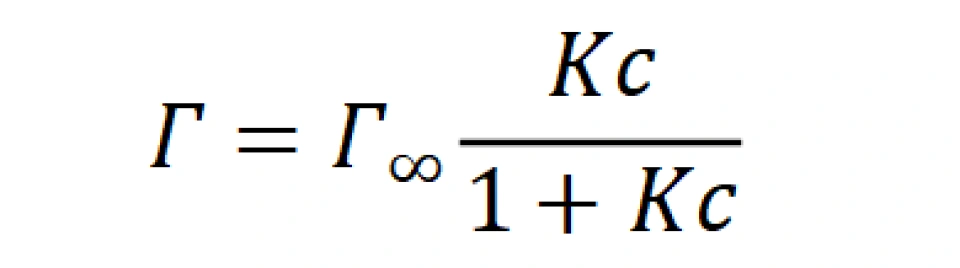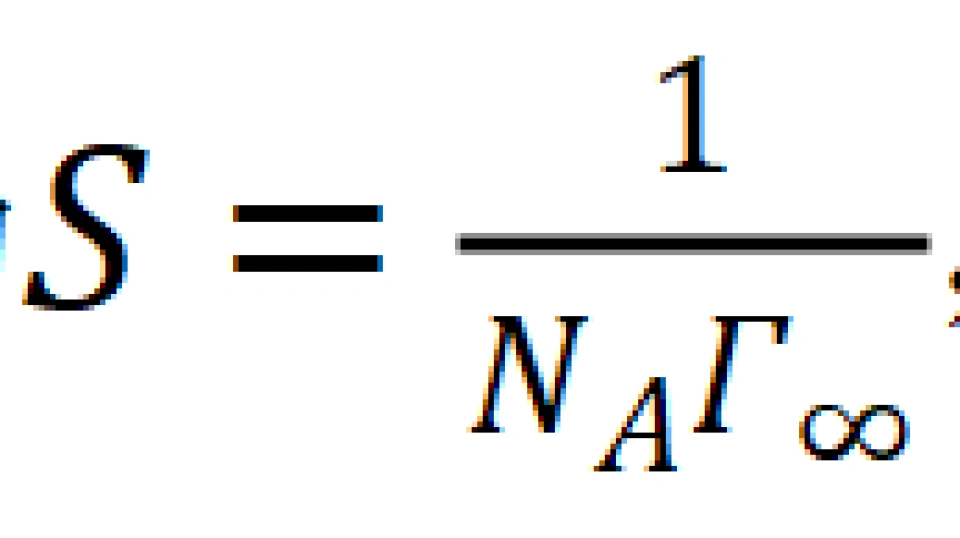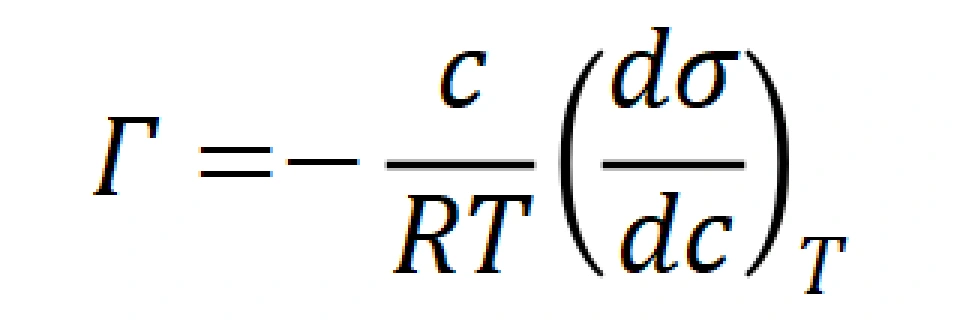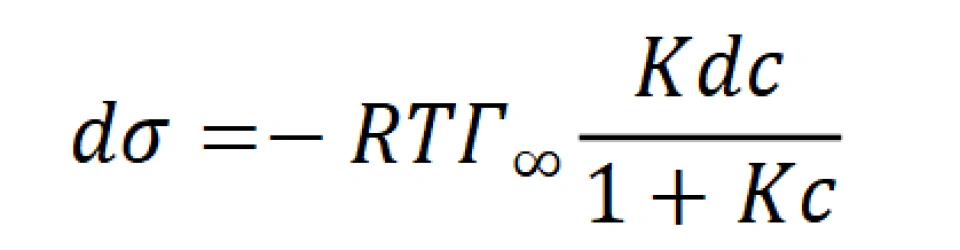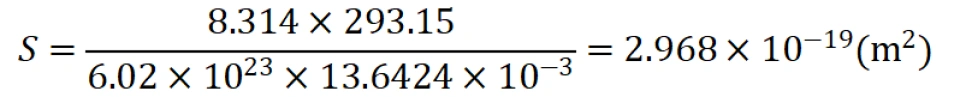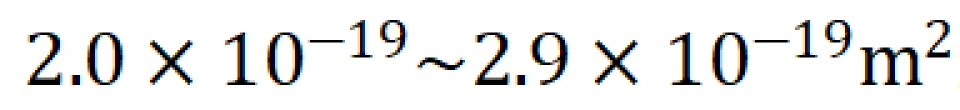没有，科普结束。
然而，初中学过卡文迪许扭秤实验的你一定不甘心就这么结束。既然物理中有这么一个方法叫做二次放大法，那么用同样或类似的方法是否可以去测量微观世界的尺度呢？
这个可以有。本篇科普所要实现的，就是尽力用一种较通俗的语言介绍一种测量分子横截面积的方法：表面张力法。
表面张力是什么？
啊这，要从这里开始解释吗？
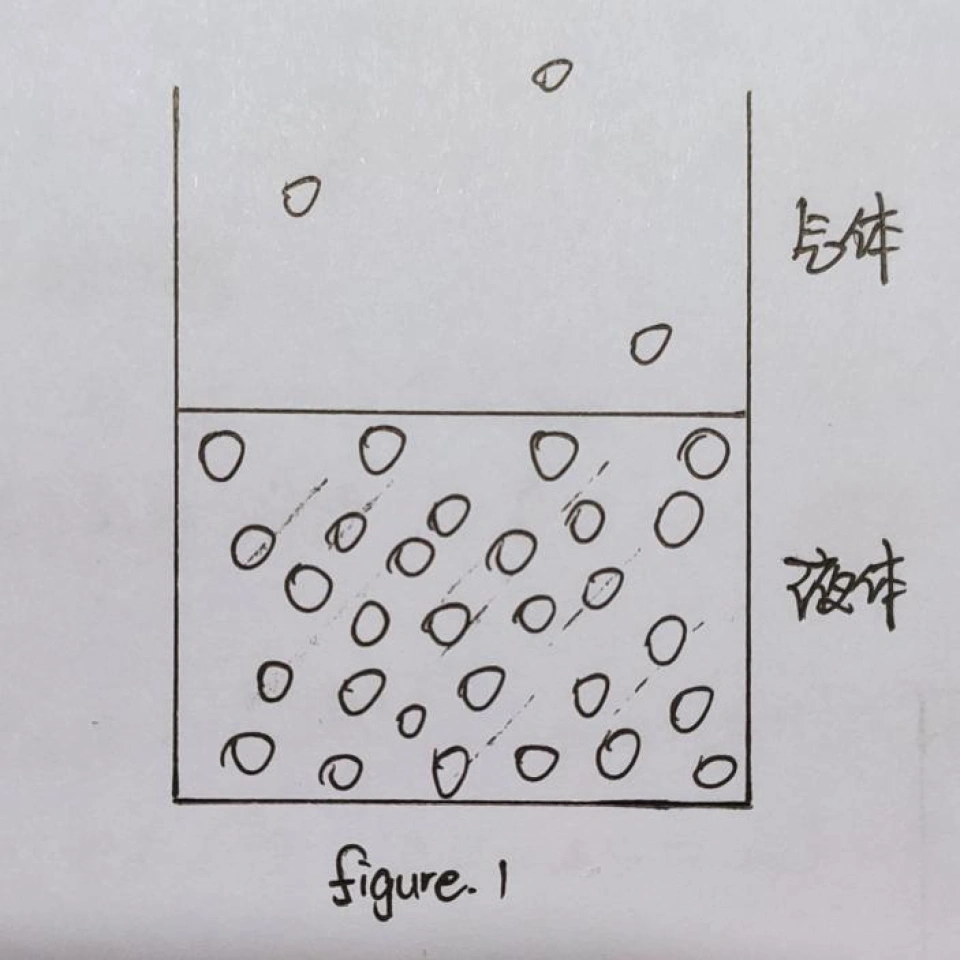
其实，表面张力的现象你已经见过不下千百回了：下雨时窗玻璃上的雨滴、清晨时绿叶上的露珠、洗衣服产生的大肥皂泡；而在高中你也已经或将要接触到表面张力的知识。从微观角度上讲，液体的内部是由很多很多分子构成的，这些分子因为相距既没有气体分子间那么远、又不如固体分子间那么近，所以表现出一种可以自由移动但又互相吸引的状态。如果用圆圈来表示分子，一杯液面接触气体的液体，其微观状态大致如下图所示。
可能已有读者注意到，在靠近液面的部分，我所绘制的圆圈——也就是分子，较稀疏。这是因为在气液分界面处考虑分子热运动，液体分子会逸散到空气中，同时空气中的分子也会进入液体；但是，在等体积情况下，液体的分子更多，因此逸散进入空气的分子也就更多，所以进入空气的分子数 > 进入液体的分子数，进而导致液体表面分子稀疏。在这种情况下，为了保证液面的连续性，在体积不变的情况下，我们要用最少的表面分子构筑表面。显然只有球面满足这一条件，而有关于等体积时球体表面积最小问题的证明，在这里不再赘述。也就是说，液体表面分子间存在一种力，使得忽略重力作用时液体表面呈球面。维持这种状态的力便被称之为表面张力。
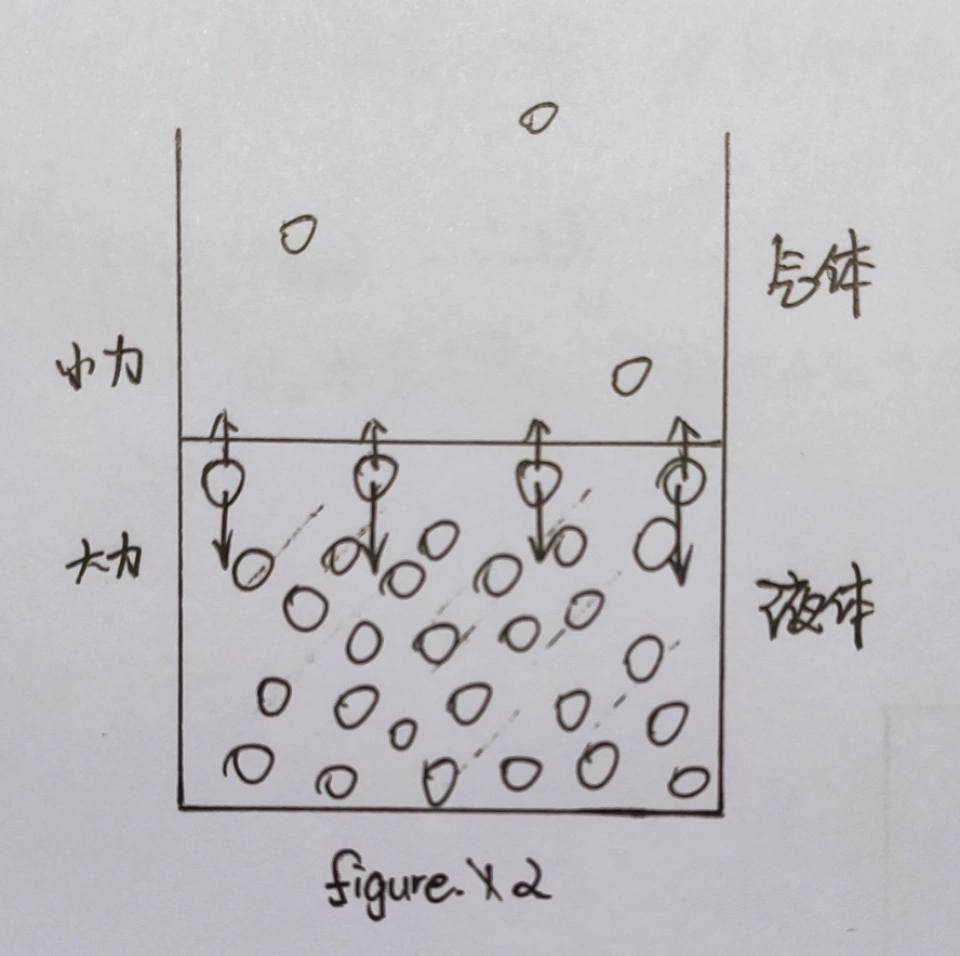
那么表面张力是如何产生的？我们还回到之前的figure 1，我再多画几笔。
（哟哟哟，这不是气体分子吗，几天没见，这么拉了）
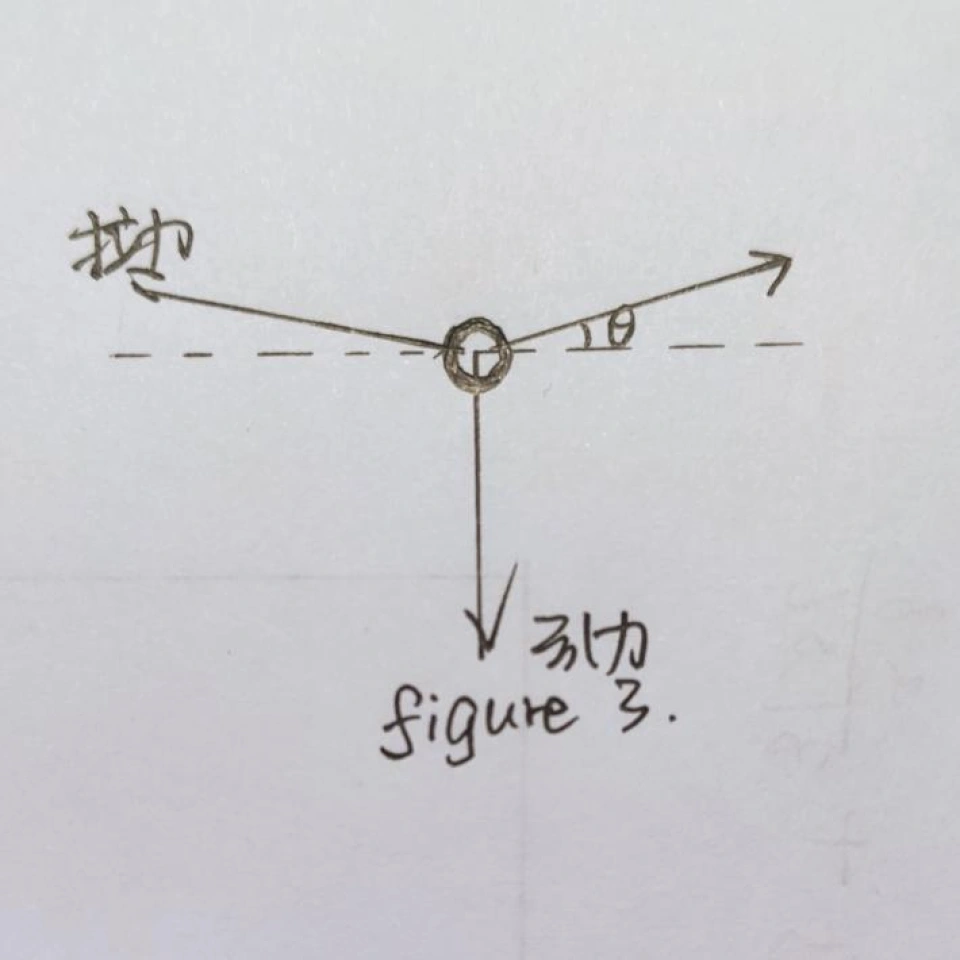
用箭头代表分子间作用力，显然液体分子“人数”更多，优势更大；气体分子就比较拉了，产生不了多少引力。这个引力差就是表面张力的产生原因（但不是表面张力本身），它让液面分子有向液体内部下降的趋势，从而保持表面紧绷。当然，这是一个比较容易通俗解释的模型，并不是真实现象，实际情况要比这复杂得多。就比如，表面张力实际上的方向是与液面相切的，那么引力差如何产生这个方向的力呢？要理解的话只能这样强行解释：引力差把表面分子向下拉，同时这个分子两侧的表面分子又拉着它不愿意让它离开，如下图。
由于这个θ角特别小，分子级别的能有多大呢？咱就直接忽略掉了，这个拉力就是表面张力，与液面相切。
上面说了这么多，都是建立在只有一种液体的前提下。如果我们往这个液体里——就以水为例，加入溶质会怎么样呢？
那一夜，我不再纯洁——
哈哈，指水不再纯净，被加了溶质。别想歪了，晚上做的实验罢了。
当溶质加入之后，水的表面张力降低，那么根据能量最低原理，表面张力能肯定越小越好，那么水表面的溶质浓度就会比水内部的溶质浓度高一些；反之，则就小一些。这种表面浓度和内部浓度不同的现象被称作表面吸附。既然有现象，就会有闲着无聊（划掉）的科学家去寻找现象的规律，就比如希什科夫斯基这个人：我百度都百度不到这个人的信息，他居然还靠自己的实验数据得到了下述经验公式：
σ＝σ₀-σ₀αln（1+c/β）
其中σ是溶液表面张力，σ₀是溶剂表面张力，都是神秘的系数，显然c是溶液浓度。
这个经验公式是否正确呢？1916年物理化学家朗格缪尔也闲着没事提出了一个猜想，那就是固体表面的原子或分子存在向外的剩余价力，它可以捕捉气体分子。这种剩余价力的作用范围与分子直径相当，因此吸附剂表面只能发生单分子层吸附，并给出了朗格缪尔单分子层吸附等温式，该式在气液界面的应用形式如下：
其中Γ是吸附量，Γ∞是极限吸附量，也就是表面全都是吸附分子时的吸附量，可近似看作极限吸附时溶质的物质的量。此时认为液体表面也只能发生单分子层吸附。如果我们能得到Γ∞，也就意味着分子横截面积为
，就回归初心了。
根据化学热力学，我们可以推导（过程比较复杂，不再展示）出吉布斯吸附方程：
将朗格缪尔公式代入，得到：
积分得到：
σ＝σ₀-RTΓ∞ln（1+kc）
与希什科夫斯基经验公式形式相同，一是可以证明其正确性，二是为我们最初的主题：测量分子横截面积找到了出口。只要能够测出表面张力和溶液浓度，并作出一条曲线，通过模拟这条曲线的函数关系式，即可得到Γ∞，进而测出分子横截面积。
溶液浓度可以通过光度计等一系列方法准确测定；表面张力则可以通过在毛细管中形成一个小气泡，用仪器测定毛细管内外压力差得到气泡的附加压力，当气泡最小时和毛细管内径相同，而毛细管内径数值可以通过先测量已知表面张力数值的液体的最大附加压力得到，此时由拉普拉斯公式可知附加压力最大并求出表面张力数值。有关拉普拉斯公式的推导和本文主要内容无关。
实战！得到正丁醇分子横截面积！
其实就是因为我实验做的是正丁醇所以实战也是这个，有设备的可以自己利用科普的原理，测测其他物质的分子横截面积。
接下来的内容就是些数据处理，不算科普范畴。感兴趣的可以看看，顺便给你们证实一下这种方法的可靠性还是比较高的。
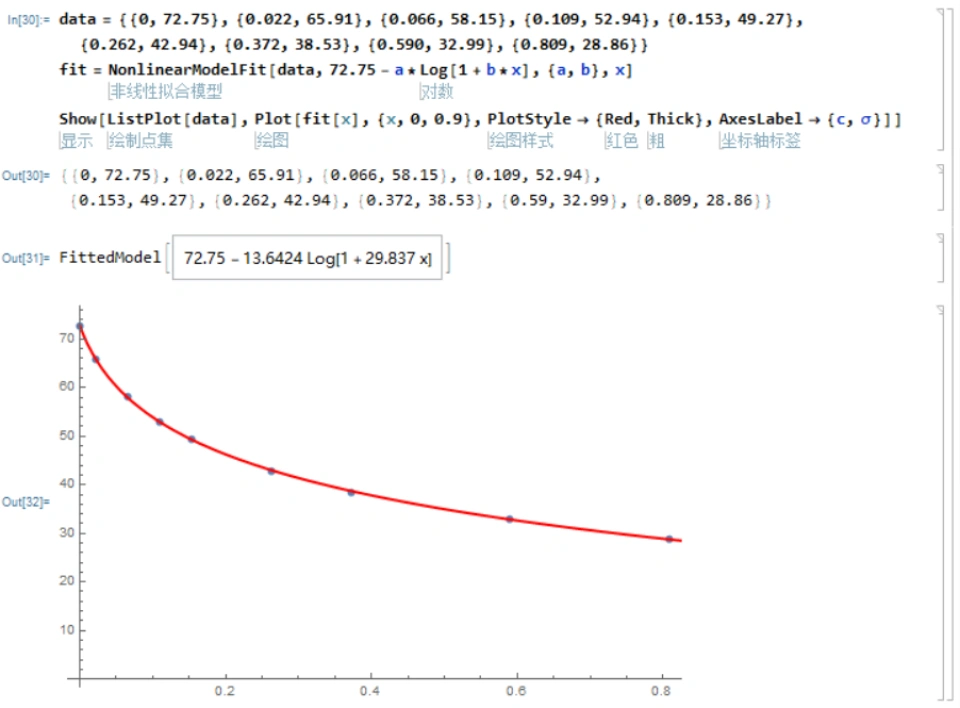
Code:
data = {{0, 72.75}, {0.022, 65.91}, {0.066, 58.15}, {0.109,52.94}, {0.153, 49.27}, {0.262, 42.94}, {0.372, 38.53}, {0.590, 32.99}, {0.809, 28.86}}
fit = NonlinearModelFit[data, 72.75 – a*Log[1 + b*x], {a, b}, x]
Show[ListPlot[data], Plot[fit[x], {x, 0, 0.9}, PlotStyle -> {Red, Thick},AxesLabel -> {c, \[Sigma]}]]
正丁醇分子横截面积在
之间，误差较小。
作者：delta
审核：观复·钧天
APC编辑部科普组
科普平台：https://jq.qq.com/?_wv=1027&k=BCtwKu2W
