斐波那契数列（ Fibonacci sequence ），又称黄金分割数列，因数学家莱昂纳多 · 斐波那契（ Leonardo Fibonacci ）以兔子繁殖为例子而引入，故又称“兔子数列”，其数值为： 1 、 1 、 2 、 3 、 5 、 8 、 13 、 21 、 34 …… 。在数学上，这一数列以如下递推的方法定义： F ( 0 ) = 1 ， F ( 1 ) = 1 ， F ( n ) = F ( n – 1 ) + F ( n – 2 ) （ n ≥ 2 ， n ∈ N * ）。
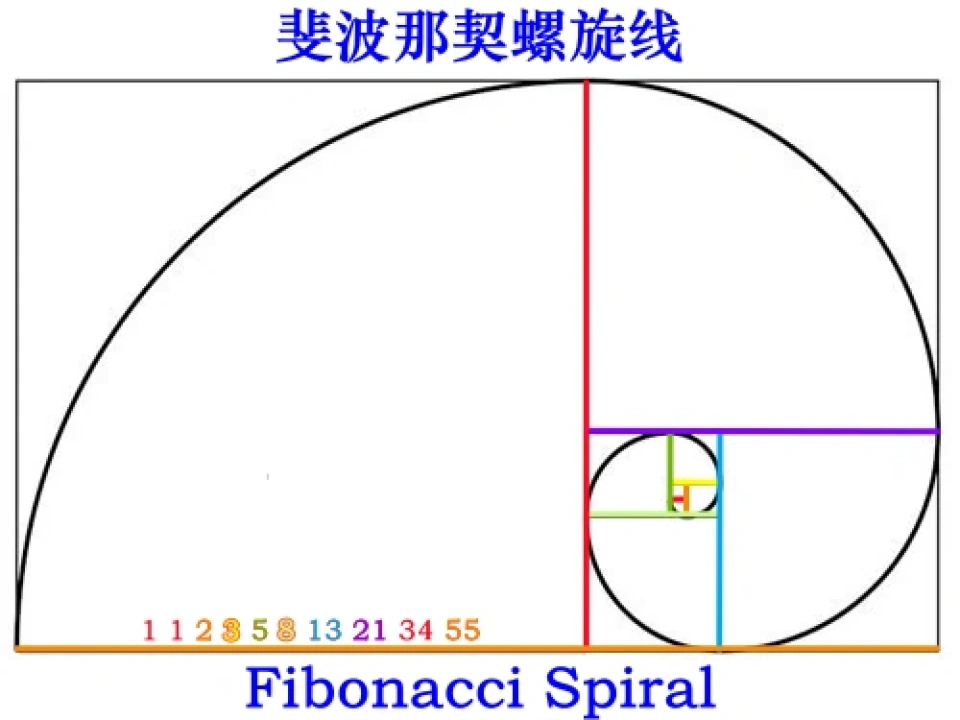
图片：斐波那契螺旋线
定义
斐波那契数列是指这样一个数列： 1 ， 1 ， 2 ， 3 ， 5 ， 8 ， 13 ， 21 ， 34 ， 55 ， 89 …… 这个数列从第 3 项开始 ，每一项都等于前两项之和。
由来
在数学历史上，欧洲黑暗时期过后，第一位有影响的数学家是斐波那契（ L ． Fibonacci ， 1170 ~ 1250 ）。他早年就随其父在非洲北部师从阿拉伯人学习算学，后又游历地中海沿岸诸国，回意大利后写成《算经》，也翻译成《算盘书》。这部很有名的著作主要是一些源自古代中国、印度和希腊的数学问题的汇集，内容涉及整数和分数算法、开方法、二次和三次方程以及不定方程。特别是，在 1228 年的《算经》修订版上载有如下“兔子问题”：
如果每对兔子（一雄一雌）每月能生一对小兔子（也是一雄 一雌，下同），每对兔子第一个月没有繁殖能力，但从第二个月以后便能每月生一对小兔子。假定这些兔子都能够活足够长的时间，那么从第一对刚出生的兔子开始， 12 个月以后会有多少对兔子呢？解释说明为：第一个月：只有一对兔子；第二个月： 仍然只有一对兔子；第三个月：这对兔子生了一对小兔子， 共有 1 + 1 = 2 对兔子；第四个月：最初的一对兔子又生一对兔子，共有 2 + 1 = 3 对兔子 …… 则由第一个月到第十二个月兔子的对数分别是： 1 ， 1 ， 2 ， 3 ， 5 ， 8 ， 13 ， 21 ， 34 ， 55 ， 89 ， 144 ， …… ，后人为了纪念提出兔子繁殖问题的斐波纳契， 将这个兔子数列称为斐波那契数列， 即把 1 ， 1 ， 2 ， 3 ， 5 ， 8 ， 13 ， 21 ， 34 …… 这样的数列称为斐波那契数列。
通项公式
斐波那契数列： 1 ， 1 ， 2 ， 3 ， 5 ， 8 ， 13 ， 21 ， 34 ， 55 ， 89 …… ，以如下被以递归的方法定义：从第三项开始，每一项都等于前两项之和，显然这是一个线性递推数列。
通项公式内容
通项公式推导
（1）方法 I ：利用特征方程（线性代数解法）
该内容详见我本人之前发布过的文章《数列的特征方程》
特性
应用
质数数量
斐波那契数列的整除性与质数生成性
每 3 个连续的数中有且只有一个被 2 整除，
每 4 个连续的数中有且只有一个被 3 整除，
每 5 个连续的数中有且只有一个被 5 整除，
每 6 个连续的数中有且只有一个被 8 整除，
每 7 个连续的数中有且只有一个被 13 整除，
每 8 个连续的数中有且只有一个被 21 整除，
每 9 个连续的数中有且只有一个被 34 整除，
…….
我们看到第 5 、 7 、 11 、 13 、 17 、 23 位分别是质数： 5 ， 13 ， 89 ， 233 ， 1597 ， 28657 （第 19 位不是）
尾数循环
斐波那契数列的个位数：一个60步的循环：
11235 ， 83145 ， 94370 ， 77415 ， 61785 ， 38190 ， 99875 ， 27965 ， 16730 ， 33695 ， 49325 ， 72910 …….
进一步，斐波那契数列的最后两位数是一个 300 步的循环，最后三位数是一个 1500 步的循环，最后四位数是一个 15000 步的循环，最后五位数是一个 150000 步的循环。
自然界中的“巧合”
斐波那契数列表面看来似乎简单有趣，然而人们发现该数列不仅与黄金分割数，组合数学及概率论等一系列深刻的数学问题关系密切，甚至发现植物枝权与叶序分布、菠萝纹理与蜂房结构等大量的自然现象也遵从斐波那契数列的奇妙构造。
例如，树木的生长，由于新生的枝条，往往需要一段“休息”时间，供自身生长，而后才能萌发新枝。所以，一株树苗在一段间隔，例如一年，以后长出一条新枝；第二年新枝“休息”，老枝依旧萌发；此后，老枝与“休息”过一年的枝同时萌发，当年生的新枝则次年“休息”。这样，一株树木各个年份的枝桠数，便构成斐波那契数列。这个规律，就是生物学上著名的“鲁德维格定律”。
另外，观察延龄草、野玫瑰、南美血根草、大波斯菊、金凤花、耧斗菜、百合花、蝴蝶花的花瓣，可以发现它们花瓣数目具有斐波那契数列： 3 、 5 、 8 、 13 、 21 …….
其中，百合花花瓣数目为 3 ，梅花 5 瓣，飞燕草 8 瓣，万寿菊 13 瓣，向日葵 21 或 34 瓣，雏菊有 34 、 55 和 89 三个数目的花瓣。
斐波那契螺旋：在大自然里存在着许多斐波那契螺旋线形态，向日葵花盘有着两组紧密盘旋的螺旋线，一组按照顺时针旋转的数目为 21 ，另一组按照逆时 针旋转的数目为 34 ，正好是斐波那契数列中相邻的两个 数且比值接近黄金分割比，而且排列的种子以中心为点四面发散形成的角度接近于黄金角；银河系中的四条主旋臂旋转分开组成大约为 12 ° 的角度，它所反映出来的螺旋形状和斐波那契螺旋线几乎完全相同；鹦鹉螺外壳截面形状为典型的斐波那契螺旋形，被认为是以斐波那契数列形成的最完美的螺旋线。
这些植物懂得斐波那契数列吗？当然并非如此，它们只是按照自然的规律才进化成这样。这似乎是植物排列种子的“优化方式”，它能使所有种子具有差不多的大小空间却又疏密得当，不至于在圆心处挤了太多的种子而在圆周处却又稀稀拉拉。叶子的生长方式也是如此，对于许多植物来说，每片叶子从中轴附近生长出来，为了在生长的过程中一直都能最佳地利用空间（要考虑到叶子是一片一片逐渐地生长出来，而不是一下子同时出现的），每片叶子和前一片叶子之间的角度应该是 222 . 5 ° ，这个角度被称为“黄金角度”，因为它和整个圆周 360 ° 之比是黄金分割值，而这种生长方式就决定了斐波那契螺旋的产生。向日葵的种子排列形成的斐波那契螺旋有时能达到 89 条，甚至 144 条。
数字谜题
现有长为 144 cm 的铁丝，要截成 n 小段（ n ≥ 3 ），每段的长度不小于 1 cm ，如果其中任意三小段都不能拼成三角形，则 n 的最大值为多少？
由于形成三角形的充要条件是任何两边之和大于第三边，因此不构成三角形的条件就是存在两边之和不超过另一边。截成的铁丝最小为 1 ，因此可以放 2 个 1 ，第三条线段就是 2（为了使得 n 最大，因此要使剩下来的铁丝尽可能长，因此每一条线段总是前面的相邻两段之和），依次为： 1 、 1 、 2 、 3 、 5 、 8 、 13 、 21 、 34 、 55 ，以上各数之和为 143 ，与 144 相差 1 ，因此可以取最后一段为 56 ，这时 n 达到最大为 10 。
我们看到，“每段的长度不小于 1 ”这个条件起了控制全局的作用，正是这个最小数 1 产生了斐波那契数列，如果把 1 换成其他数，递推关系保留了，但这个数列消失了。这里，三角形的三边关系定理和斐波那契数列发生了一个联系。
在这个问题中，这个 143 是斐波那契数列的前 n 项和，我们是把 144 超出 143 的部分加到最后的一个数上去，如果加到其他数上，就有三条线段可以构成三角形了。
推广
相关的数学问题
隐藏内容需要登录才可以看见
注意：原图有水印遮挡，建议大家到BD百科去查看词条“斐波那契数列”