周长( C )和面积( S )是平面封闭图形的两个基本属性。椭圆( Ellipse )作为平面封闭图形,自然也会存在周长( C )和面积( S )这两个基本属性。椭圆( Ellipse )的面积( S )很好计算,由圆的面积公式( S = π r ↑ 2 )以及平面坐标变换规则,很容易导出 S = π a b ,至于它的周长,应该如何计算呢?
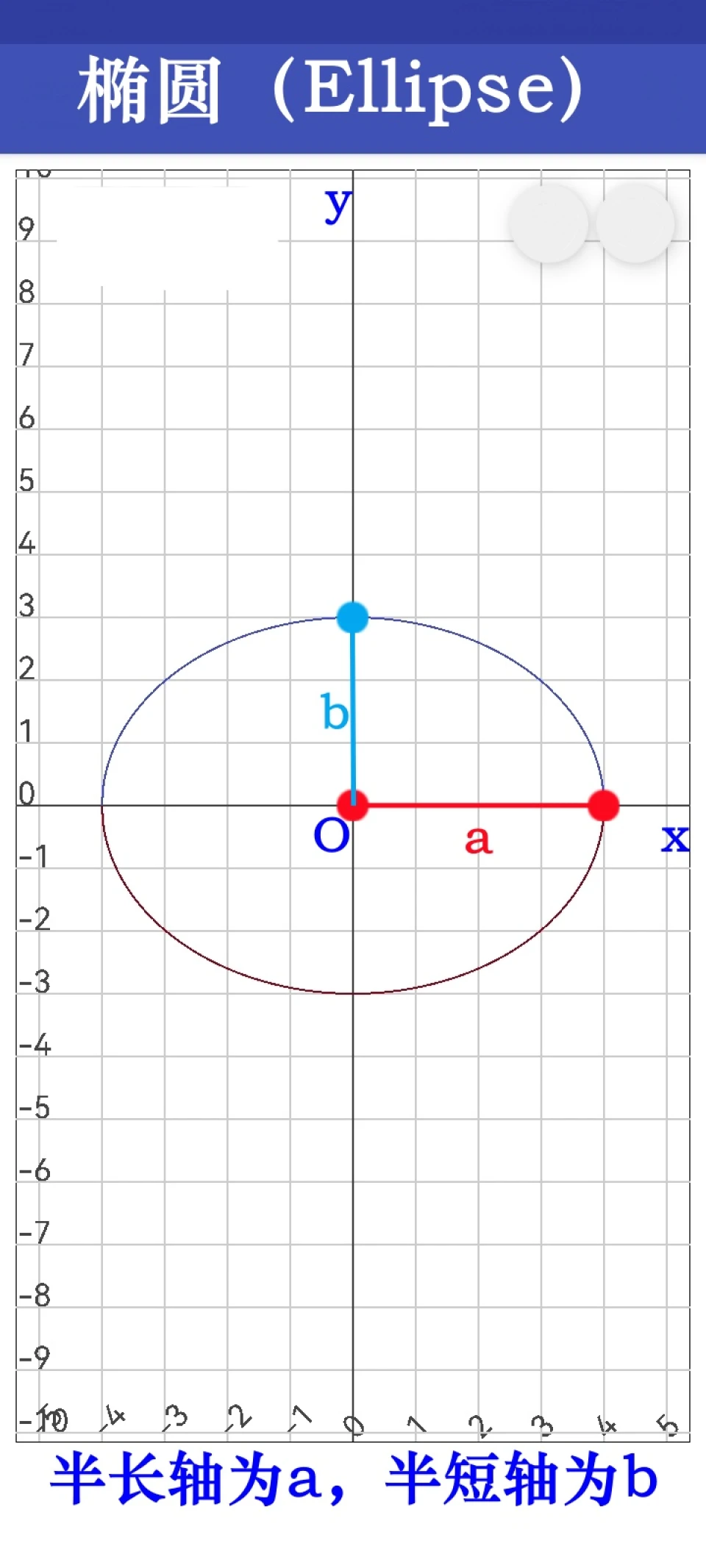
图片:椭圆( Ellipse )
事实上,有关椭圆周长的问题,最早由欧拉( Euler )提出,经过了勒让德、高斯、阿贝尔和雅可比等人的发展,并且从这类问题的讨论中,还专门引出一门数学分支——椭圆积分与椭圆函数。
那么,椭圆的周长有没有公式呢?答案是:椭圆周长没有精确的初等公式,但有非初等的椭圆积分形式的表达及其级数展开式。
在BD百科“椭圆”一词条中明确指出:椭圆周长的计算公式为 C = λ( a + b ),其中, λ 为椭圆周长系数,由 a / b 的数值决定, a 与 b 分别为椭圆的半长轴和半短轴。当 a = b 时(即椭圆为正圆时),λ = π 。详细的椭圆系数简表,请大家自行去查看BD百科词条“椭圆”。
或许有些人认为,可以从函数图像的曲线长度公式(详见我本人之前发布过的文章《用微积分的方法求解花瓶的侧面积》)来推导椭圆周长的理论公式。具体过程如下:
但是,如果你将具体的 a 、 b 的数值代入由该过程导出的椭圆周长理论公式,你就会发现, C 的数值很难计算。
首先,我们来看一看简单的近似计算方法:
首先是最为简单的椭圆周长近似计算公式: C = 2 π b + 4 ( a – b ),这些公式均符合椭圆的基本规律,当 a = b 时, C = 2 π a 。
在以下公式中:
公式 I 至公式 VII 为一般精度近似公式,满足简单计算需要;
公式 VIII 为高精度近似公式,满足比较专业一些的计算需要。
IX:一个高精度的近似公式,精确度可由使用者自由控制,具体如下:
X:精确度最高的近似公式,具体如下:
那么说到这里,有人会问:
椭圆周长的真正理论公式是什么?
现在,让我来为你解答,具体见下:
推导过程如下:
事实上,关于椭圆周长的理论公式,清代数学家项名达( 1791 ~ 1850 )也有所发现。该公式被称作“项名达公式”,为一条无限级数展开式,具体如下:
隐藏内容需要登录才可以看见























圆的中心点是一个椭圆的点有两个。
π是由周长和直径推导的也有微积分的推导方式,那其实就是画个圆剪下来测量直径与周长不同大小的圆得到的结果……也是一种积累吧
注意:原图有水印遮挡,建议大家到BD百科搜一下“椭圆周长”
如果你想求一个半长轴为 a ,半段轴为 b 的椭圆的周长,你可以参考以下的方法:
I、登录“https://zh.numberempire.com/”,然后点击“定积分计算器”
II、输入需要积分的函数表达式“(2/a)*sqrt((a^4-a^2*x^2+b^2*x^2)/(a^2-x^2))”,设置自变量 x 的范围为“从: - a 到: a ”,然后点击“计算”
III、计算出来的结果,即为该椭圆的周长
注意:在此过程中,你需要输入的是 a 与 b 的具体数值
输入格式参照下图所示: