相信大家都有这样的一个直觉:任何空间图形的表面积和体积都是有限的。但是,今天这一篇文章可能让你难以置信。
托里拆利小号(Torricelli's Trumpet),是由意大利数学家埃万杰利斯塔·托里拆利(Evangelista Torricelli)所构造出的一个表面积无限大但体积有限的三维几何体。说到“托里拆利”,大家很自然地就会想到“托里拆利实验”(就是用玻璃管里的汞柱高度测定大气压的实验)。这个三维几何体,实际上就是将函数f(x)=1/x的图像在x≥1的部分围绕x轴旋转一周所得到的图形。由于这个图形的样子很像小号,所以被叫做“托里拆利小号(Torricelli's Trumpet)”。
图片:小号
图片:托里拆利小号(Torricelli's Trumpet)
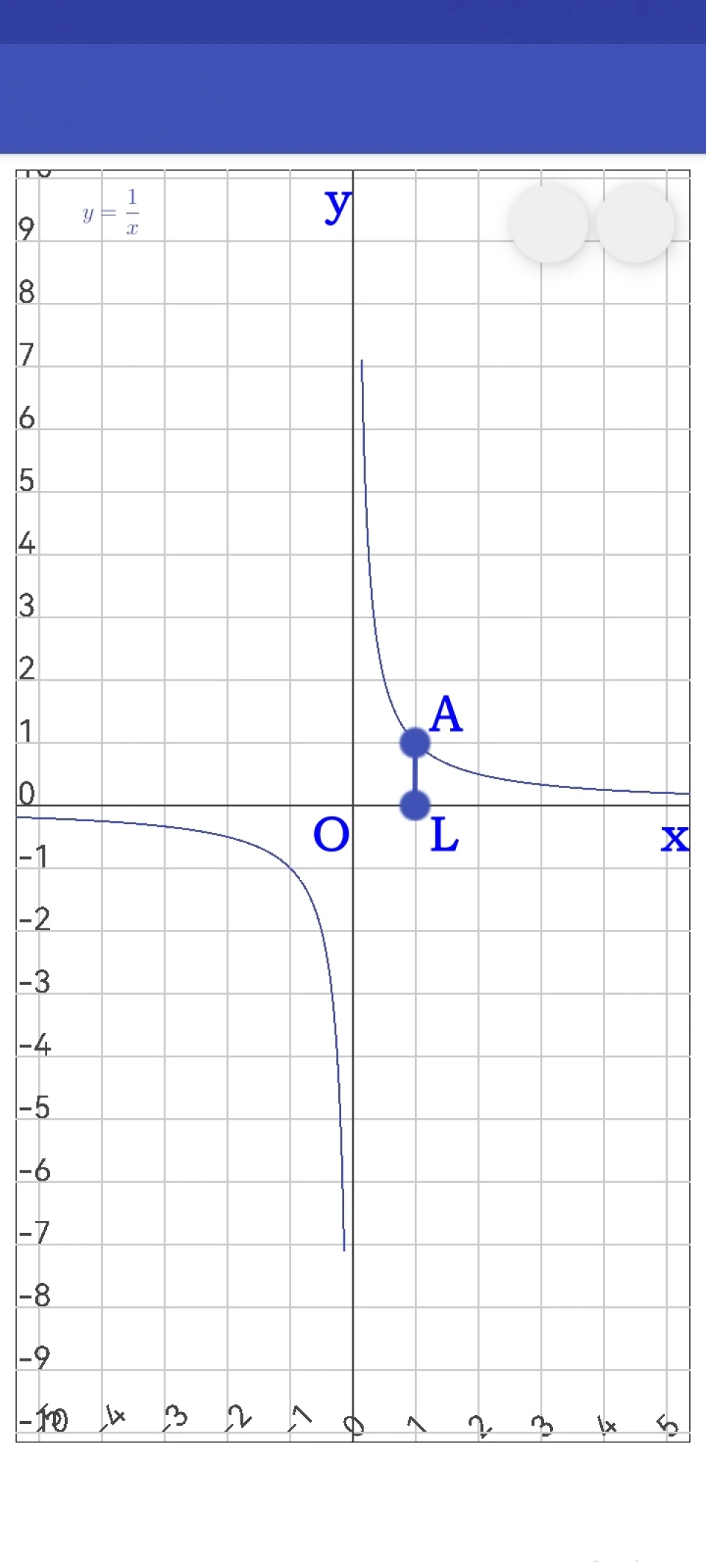
图片:函数f(x)=1/x的图像
接下来,我用微积分的方法来说明托里拆利小号为什么体积有限而表面积无限,过程如下。
体积有限:
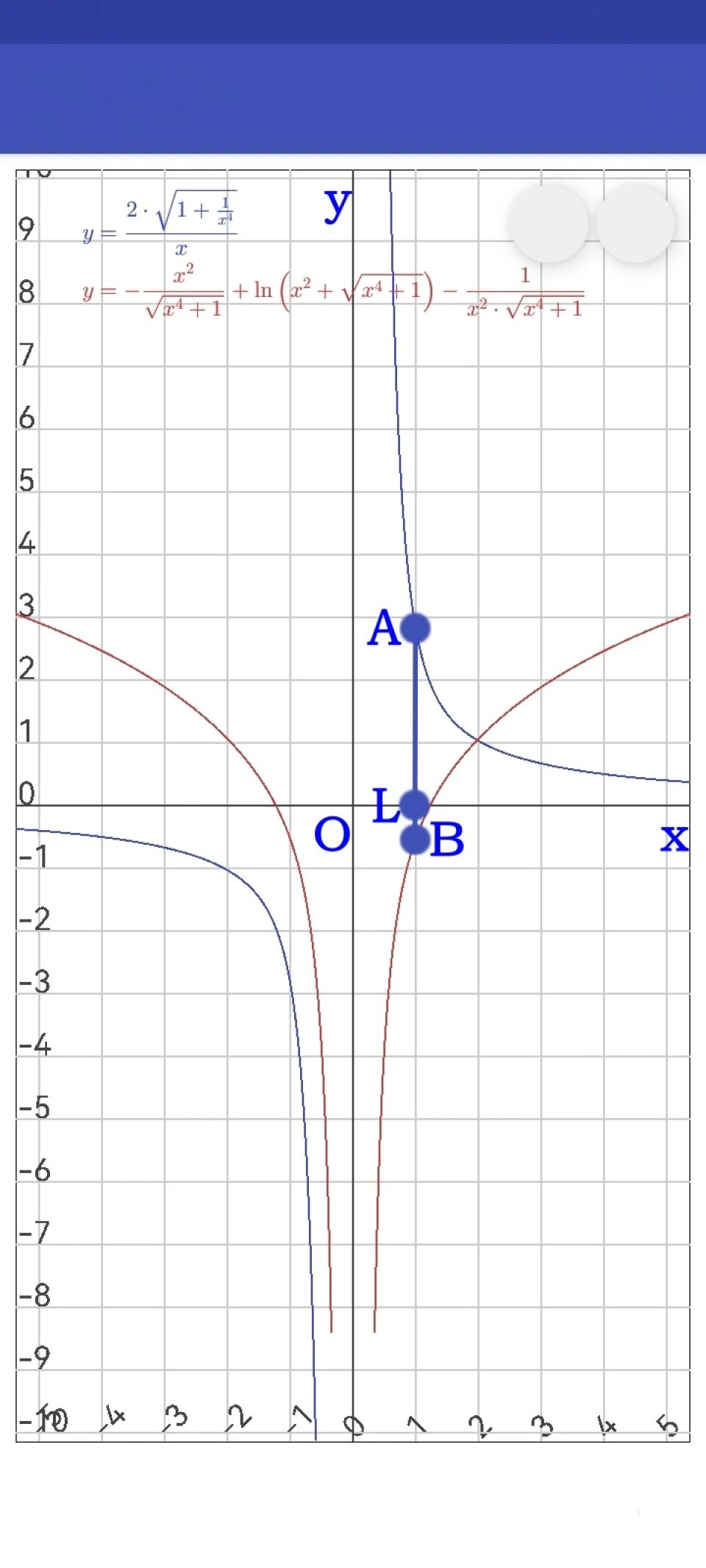
表面积无限:
所以,托里拆利小号(Torricelli's Trumpet)是一个体积有限但表面积无限的立体图形。




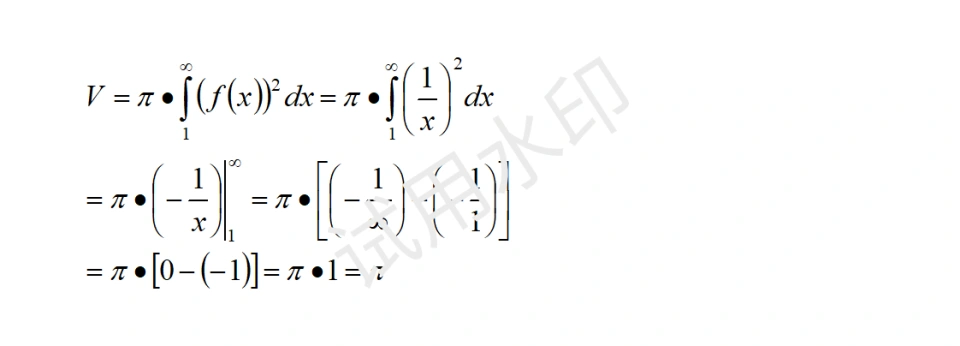















下期精彩:揭秘塞德娜(Sedna)
注:本文中所用的“瓶侧面”的面积公式,我本人之前做过推导,详见《用微积分的方法求解花瓶的侧面积》