科普驿站 第二期
科目：物理/天文
难度：B2-C1
讲师：弦轴子
接下来我们介绍第二个概念——彭罗斯图
彭罗斯图
彭罗斯图是闵可夫斯基时空图的广义相对论推广，它是一个共形图或者是经过共形变换。
所谓的共形变换可以认为是保角变换，所以就不难看出为什么在广义相对论中扩展这个东西。同时它可以改变尺度，其特征就是趋于无穷远时趋于0，这正是我们要找的。
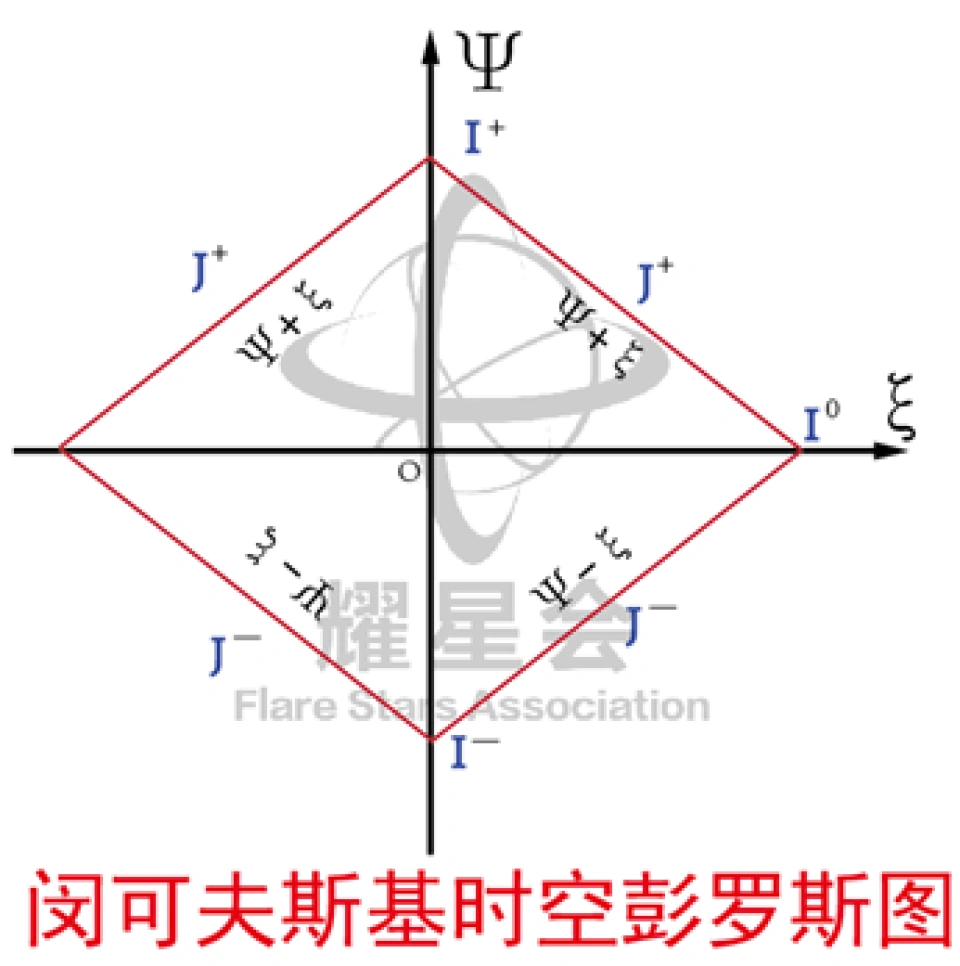
现在我们来简单看一下闵可夫斯基时空的时空图是怎样经过共形变换得到闵可夫斯基时空的彭罗斯图的。
首先，我们依旧采用球坐标系 
，
闵可夫斯基时空时空线元为：
后面那串 
就不看它了，只考虑t与r。
为了方便， 
下面也就不写了。
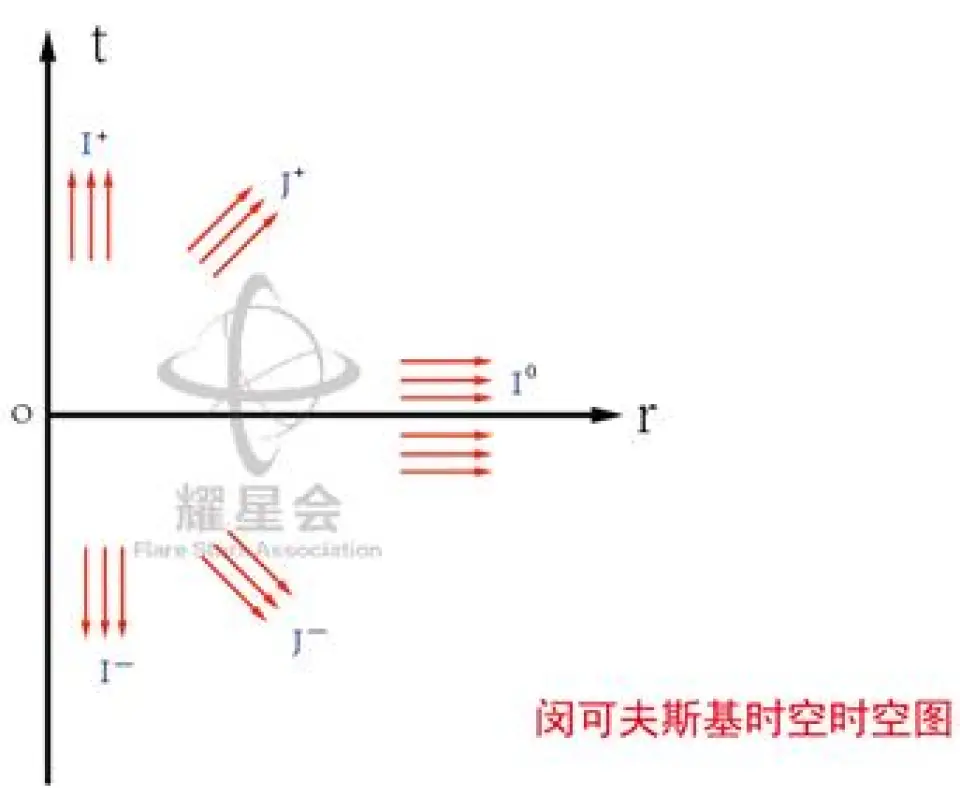
此图是闵可夫斯基时空“无穷远”的示意图，此图中一点对应着一个r=常数的球面。
引入坐标变换 
令 
在广义相对论中，如果时空的尺度发生压缩，如果还用原来的时空图，光锥的角度势必会变化。为了保持原时空中45度角的光锥不变，所以在广义相对论中用这个东西。
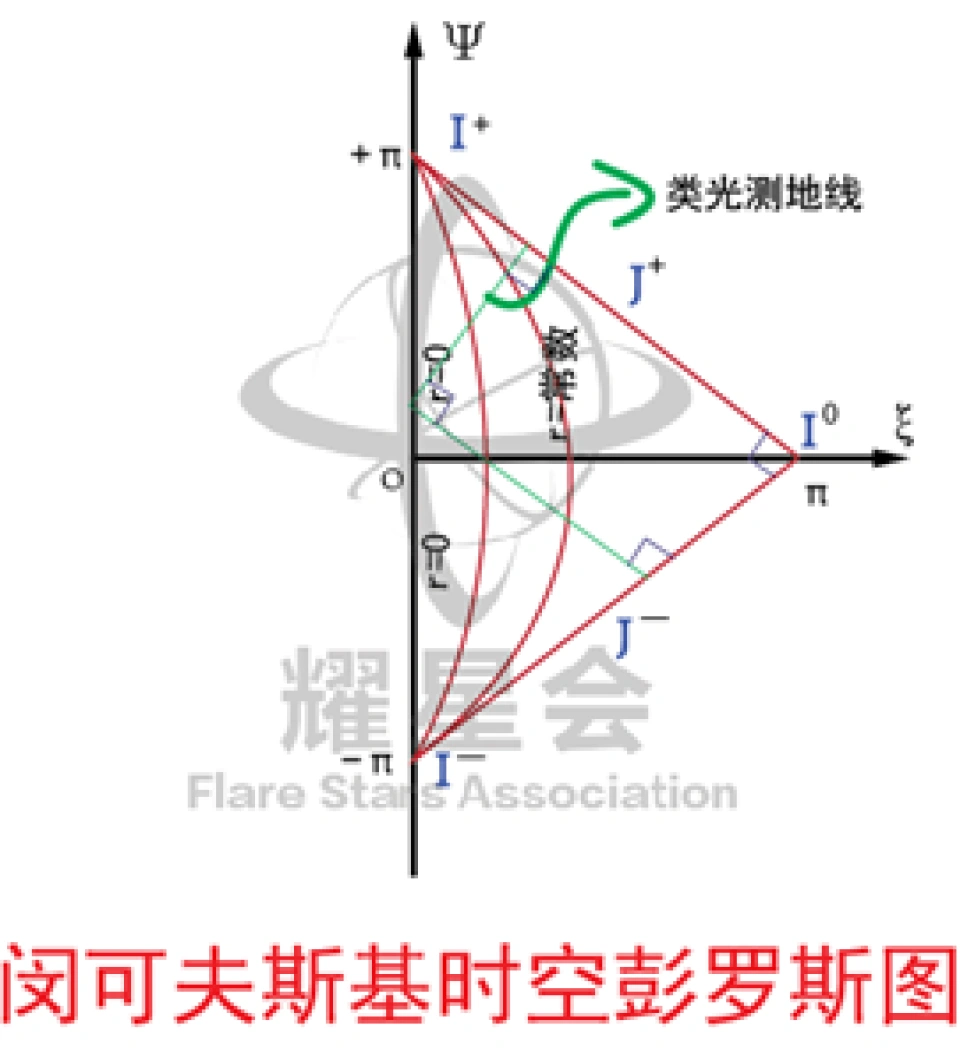
等时间线和等空间线上，对应的时间和空间坐标是相同的，在这里是弯曲的，目的是为了保持，无论怎么样，原来时空中呈45度的光锥仍然是45度，也就是光的世界线夹角仍然是45度。
所有低于光速运动的观察者走世界线一定是这些等空间线或者平行于它们。
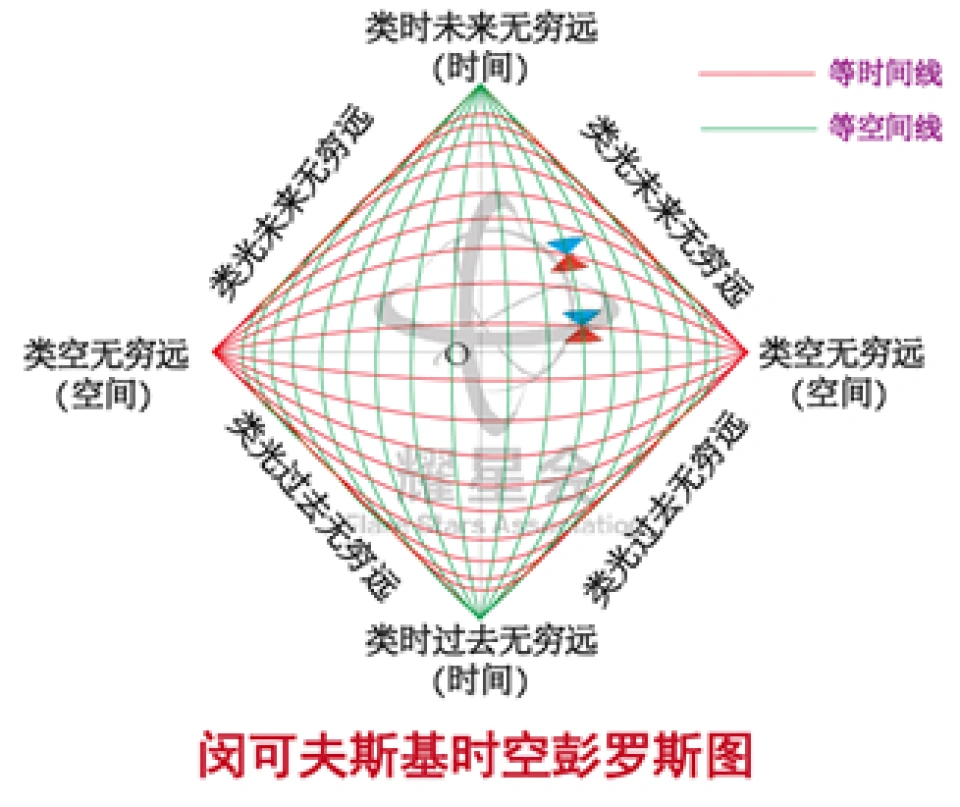
当然，通常我们看到的彭罗斯图是没有把那些等时间线和等空间线表达出来的。
关于彭罗斯图具体怎么来的？数学形式是什么？这里就不讲了，感兴趣的可以去翻任何一本广义相对论和教材翻到相对应的地方。
现在我们考虑史瓦西时空，
史瓦西时空就是四维微分流形附带史瓦西度规亦即： 
。
史瓦西度规为：
史瓦西时空时空线元为：
我们采用球坐标系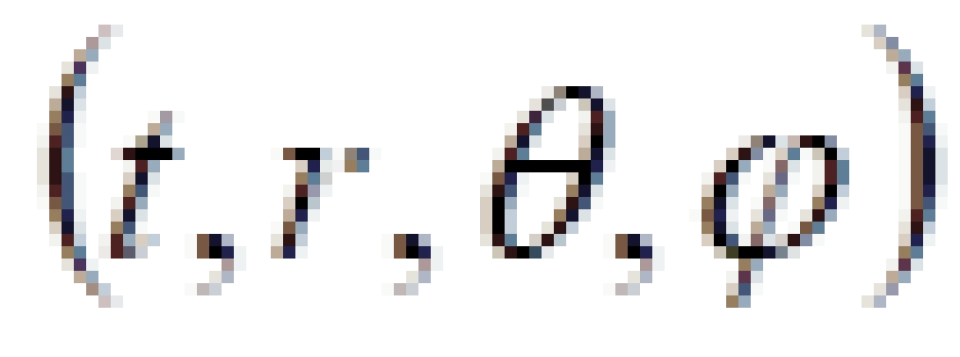 
，上面在直角坐标系
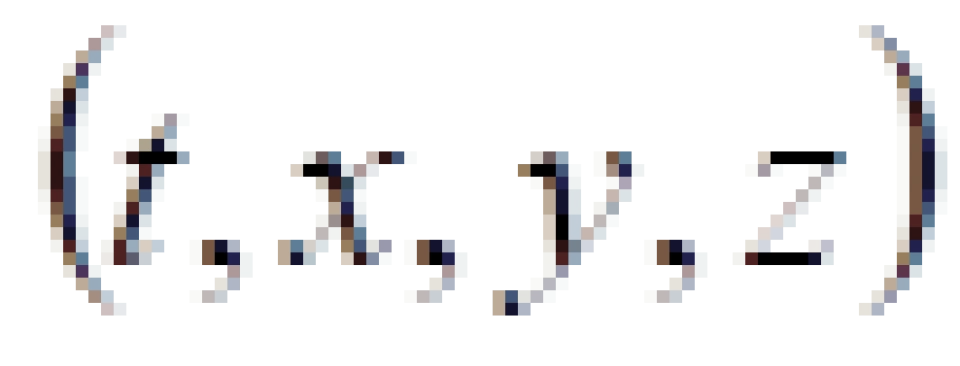上中史瓦西时空时空线元改为：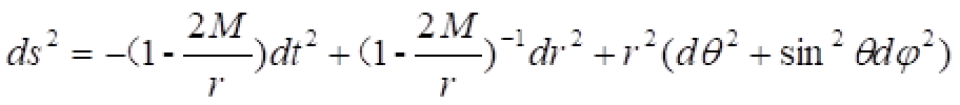
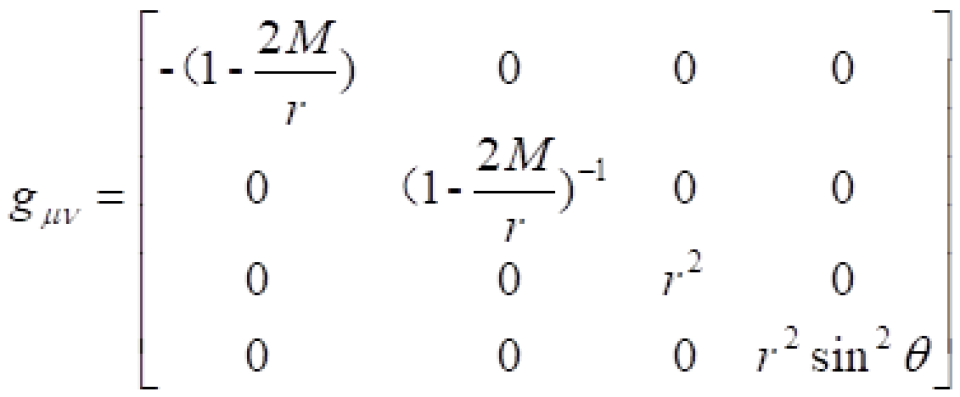
史瓦西时空线元来源于爱因斯坦场方程的史瓦西解。它是假设一颗天体没有自转，静态，它的引力场具有球对称性。有了这些限制条件就可以大大减缓难度，这样得出来的解。我们可以将直角坐标系的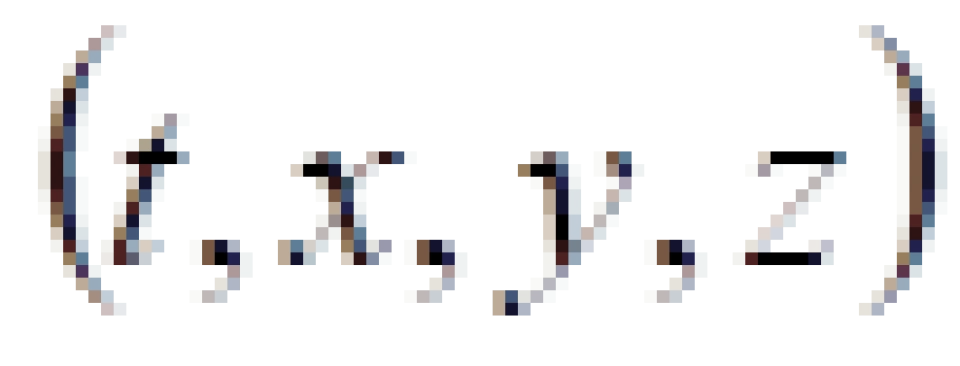 改成采用球坐标系 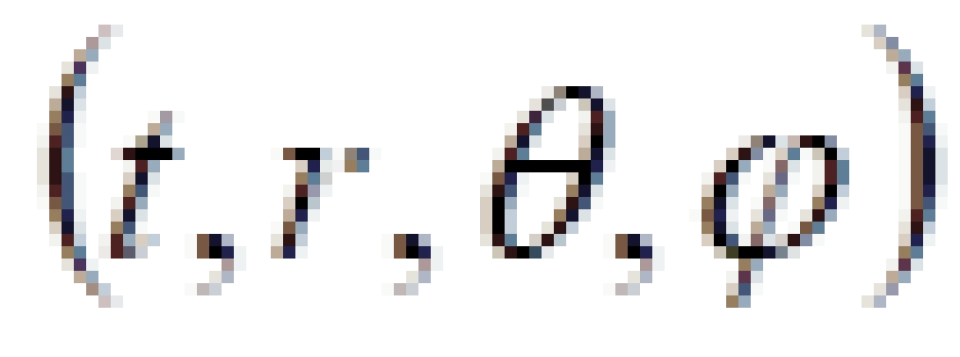，这样更容易看出球对称性。
这样我们将会得到一个应该是第一个最精确场方程的解一一史瓦西解。它是描述静态没有自转而且具有球对称性的时空。但是它分了两部分，就一种是天体内部的，还有一种是外部的真空解。
球坐标系下的史瓦西时空的时空度规线元是这样的：
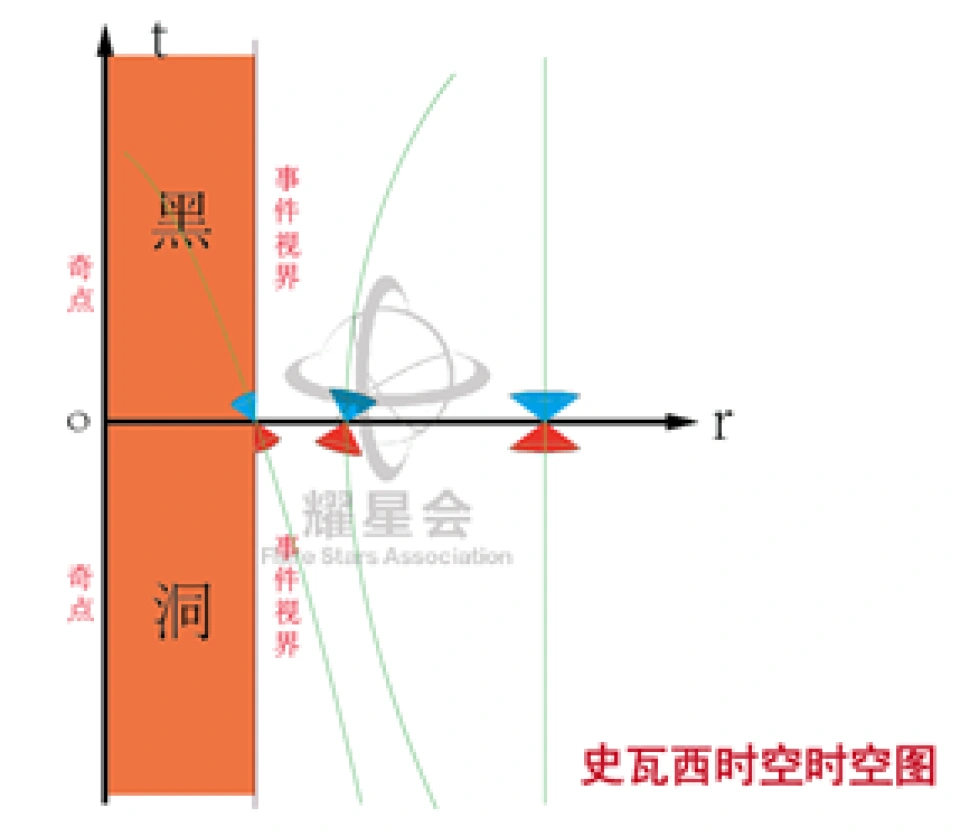
现在我们来看看史瓦西时空的时空图长啥样子。
可以看到，越靠近于史瓦西黑洞，这些世界线就越弯曲，即使是光线也不例外，而且光线再也不是保持45度夹角了。对应的就是光锥越来越扭曲，前端越来越窄，这意味着低于光速的观察能够选择的空间越来越小，越靠于黑洞，就越来越窄，最终只能选择撞上事件视界这条路。
不过这张图并不友好，因为光锥是高度扭曲的，不能保持45度夹角。
因此，如果我们采用彭罗斯图，就会更好一点。
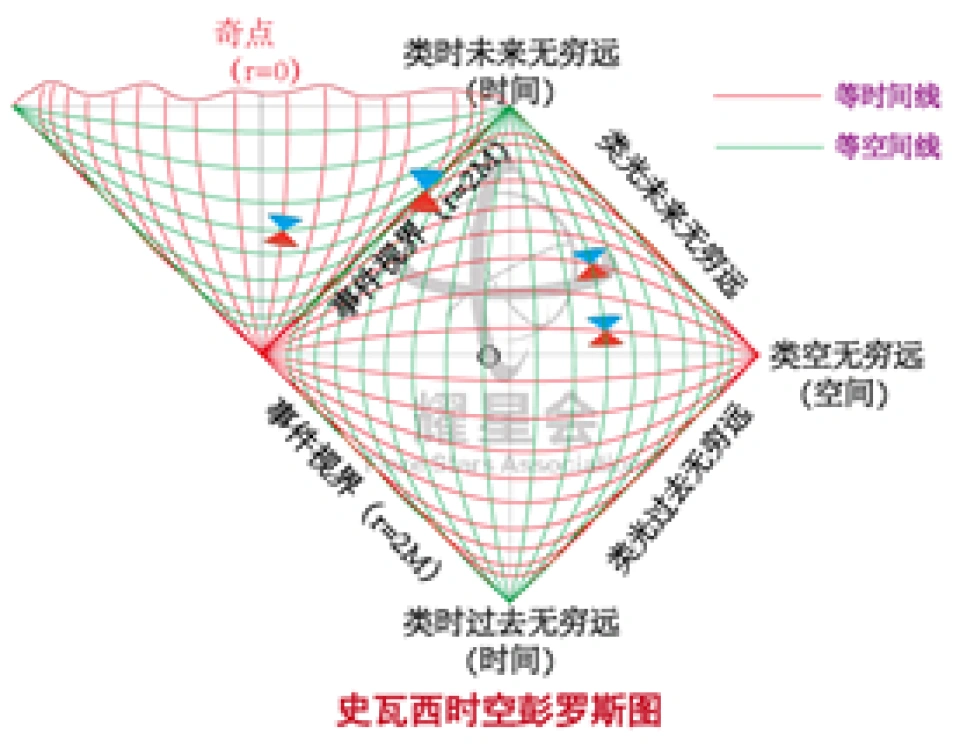
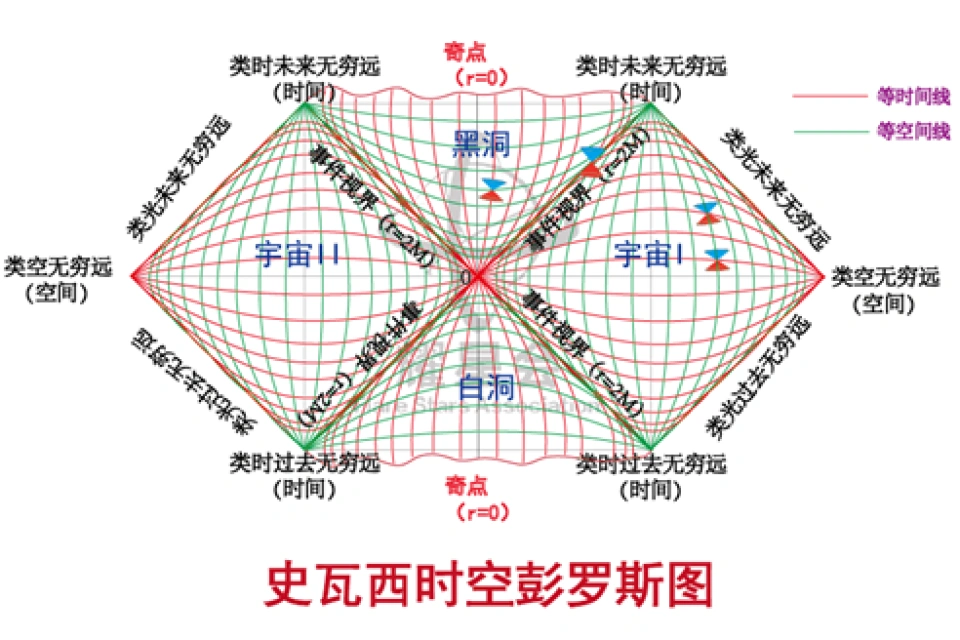
那么史瓦西时空的彭罗斯图就是这样子的。（与我们上面定义闵可夫斯基时空的彭罗斯图类似，有能力的读者可以自己推导一下，练练手）
从彭罗斯图可以看到直观清楚的看到物体到黑洞内部会发生什么。
时空坐标互换
我们会发现，此时的时间的尽头再也不是未来时间无穷远处而是奇点处。
说明到达黑洞内部的物体会不受任何阻碍的撞向黑洞奇点处，就如同外界的人时间会向未来流折逝一样。这种现象被称为时空坐标互换。因为在这里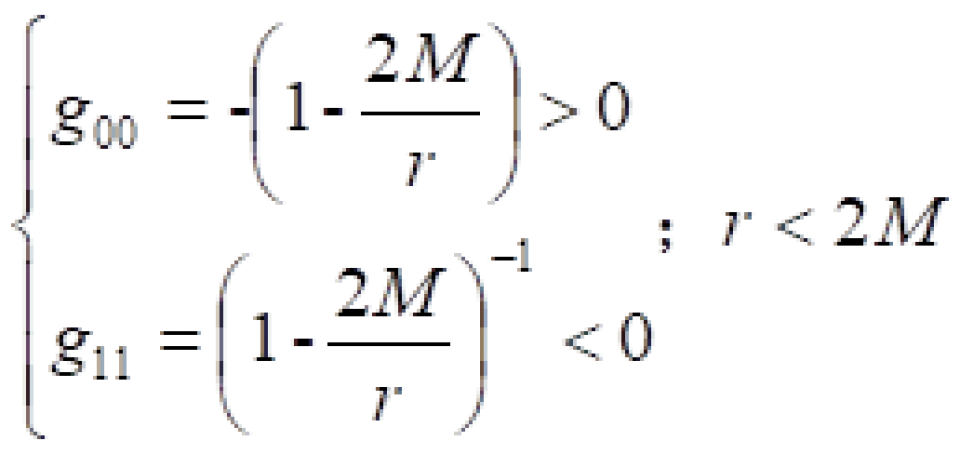
，我们说过，时空度规的一正三负正好对应着一个时间和三个空间，但是这里的时空度规对角元素00项与11项正好颠倒过，谁小于零，谁是负的正好代表时间的角色。谁大于零就代表空间的角色。因此，在这里时间坐标t充当空间的角色，而是空间坐标r充当时间的角色。
史瓦西黑洞的奇点/奇异性，也就是r=0就变成一个等时面。这个面跟时间方向垂直。这种奇异性被称为类空奇异性，所以史瓦西奇点被称为类空奇点。
而且我们可以知道，即使在这个时候光锥仍然是45度角，也就是无论什么时候光速始终不变，始终是真空中的一个那个定值。
并且黑洞是一个单向膜，黑洞内部没有一个物体能够离开黑洞都会撞向奇点。
我们都知道，黑洞内部有一个奇点，它会导致时空曲率发散，通俗来讲就是引力无限大。
这是球坐标系下的史瓦西时空的时空度规线元是这样的：
这里我们可以知道有两个地方可以导致发散，第1个地方就是当r=2M时，也就是事件视界处。第2个地方当r=0时，也就是黑洞奇点处。
我们讨论第1个地方，这个地方的发散导致我们必须用两个坐标才能描述黑洞外部和黑洞内部。任何计算，包括时间都将在这事件视界处发散，无限大。这也就是通常讲的，对于黑洞外部的观察者来看，越靠近黑洞事件视界的时间变得越慢，到黑洞事件视附近处，对于外界观察者来看几乎是无穷长的时间了。但是其实这种结果是我们采取一个不完善的坐标导致的。我们采用的史瓦西坐标并不能描述事件视界这处，这就好比极坐标无法描述原点一样，但是直角坐标系就可以。因此我们可以选择合适的坐标系来消除这种发散的地方，我们也把这种发散称之为坐标发散。当然对于第2个地方，黑洞奇点处的发散是时空本身的发散，换任何坐标系都没用，估计只能换理论。
最终人们找到了能够覆盖整个史瓦西时空的坐标系，被称之为克鲁斯卡坐标系。
史瓦西坐标与克鲁斯卡坐标之间的关系是这样的：
史瓦西时空中的线源就可以变成这样：
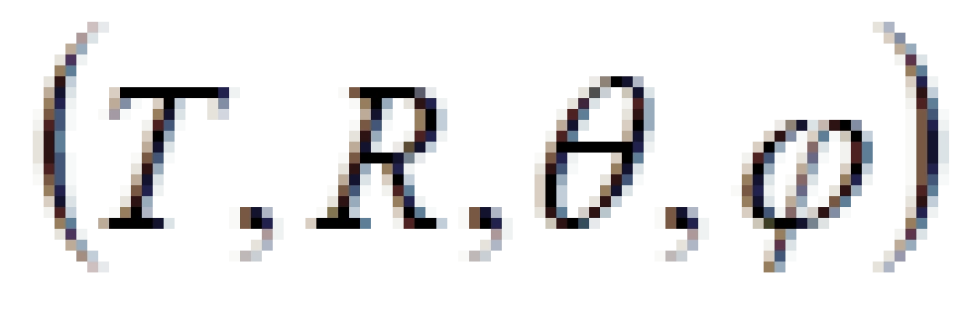就是引入的克鲁斯卡坐标，由于
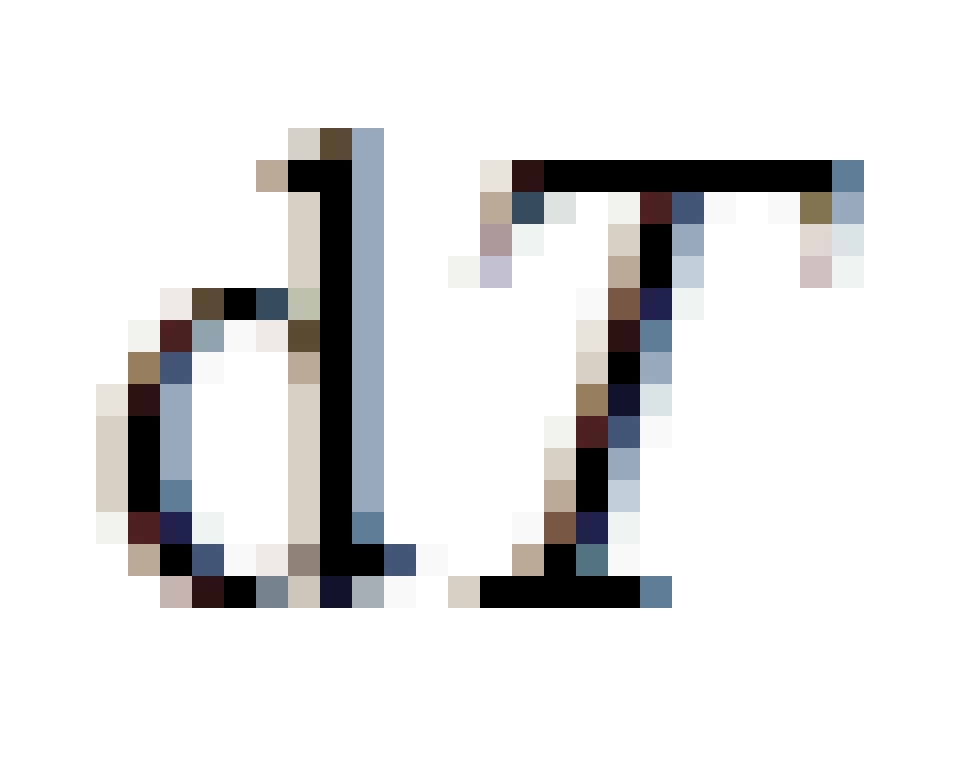前面的系数是负的，其他三个前面的系数是正的，包括 
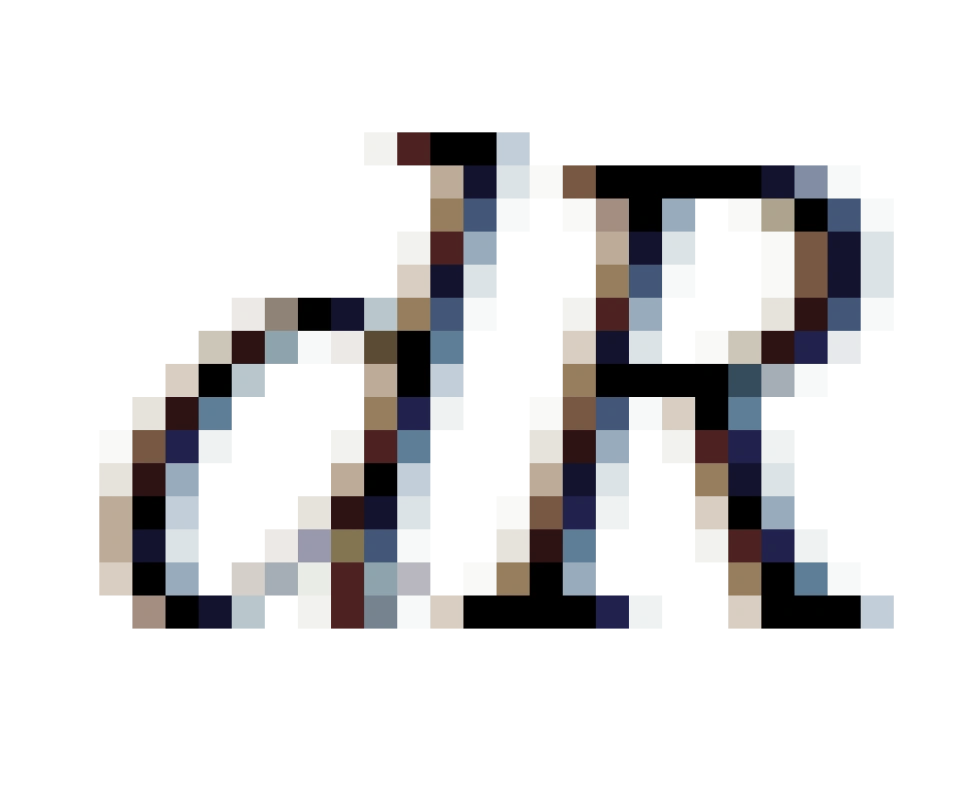的。因此，我们可以判断，T是时间坐标，R为空间坐标的某一个。
我们也可以得到r，T，R三者之间的关系，它们为：
这样可以发现，在克鲁斯卡坐标系中，r=2M处的奇异性消失了，也就是坐标不再发散。
因此，其实之前对于黑洞事件视界处的时间无穷大的推论是错误的，或者说时间坐标是发散的，但是物体实际经历的时间或者是固有时间不是发散的，是一个有限值。也就是说物体掉落黑洞这个过程的时间是有限的。
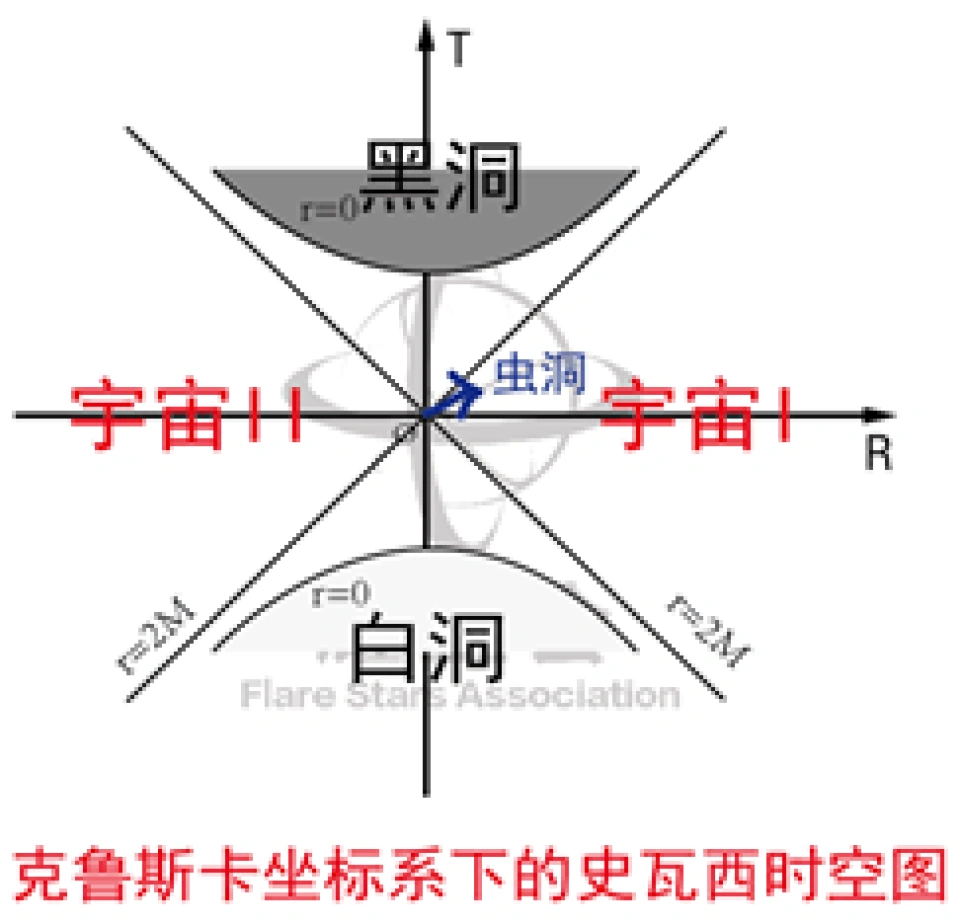
这样引入的克鲁斯卡坐标系就可以统一整个史瓦西时空，那么他的时空图是什么样子呢？
这里，上面两个双曲线r=0代表的是奇点处，两个双曲线的渐近线代表的是事件视界。
左右两个区域代表两个宇宙。F区，代表的是黑洞区，P区代表的是白洞区。
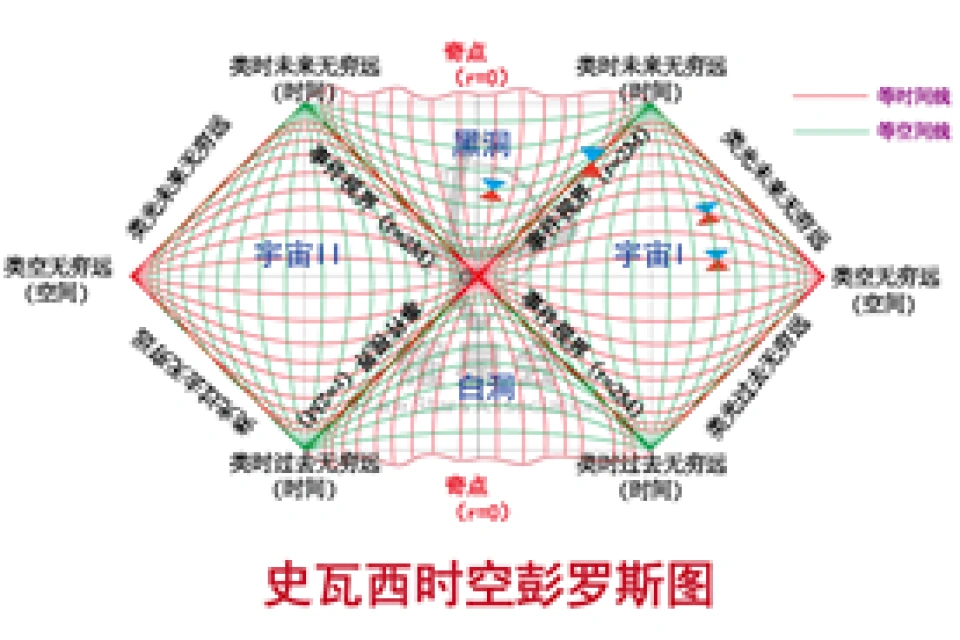
可能这样很难理解，但是当我们画出它的彭罗斯图时，一切就明朗了。
我们可以发现，在白洞区附近，任何物体都要离开，在白洞区内部，没有任何东西可以到达奇点处的。
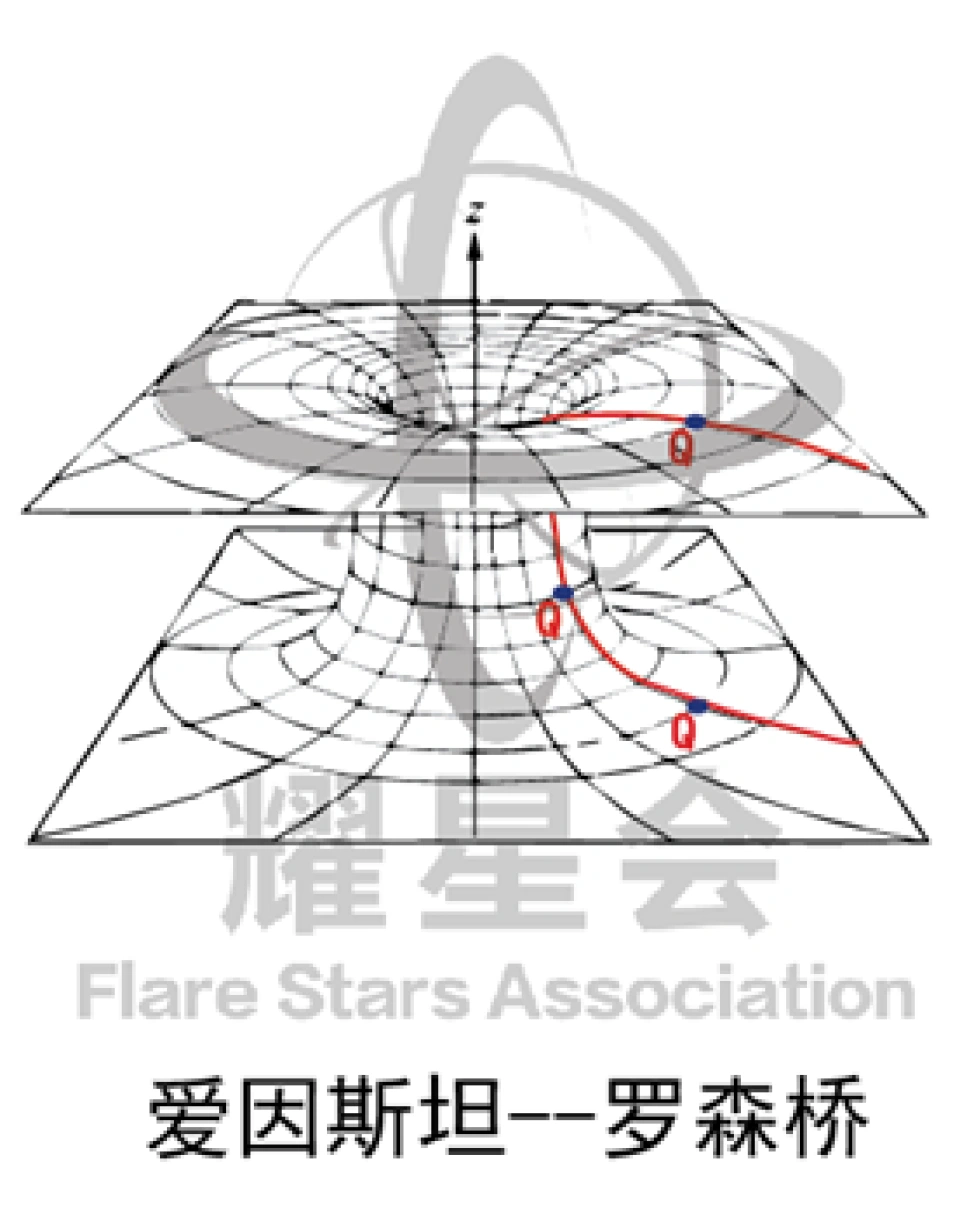
左右两个宇宙是没有任何因果关联的，连接它们的叫做爱因斯坦一一罗森桥。
这个喉，H处，其实在这张彭罗斯图上就是O点处，它是连接这两个宇宙的。
但是没有任何一条类时，类光世界线可以经过，能够经过的就只有类空世界线，可那玩意只有超光速才可以。
这是最简单的虫洞一一史瓦西虫洞，它是根据史瓦西度规改造而来的。我们也要我们也用新的物理图像工具一一彭罗斯图说明了这种虫洞是不可穿越的准确来说就是只允许类空世界线走的，因此，它没办法被改造成时间机器，除非我们超光速。
聪明的你一定会想到，既然我们解出了史瓦西度规，那么广义相对论中的其他度规呢？是有的。
比如克尔黑洞，其内部不同于史瓦西黑洞。
下面我们就来简单说说这个情况。
对于克尔黑洞，其实就是广义相对论的克尔解。它是考虑旋转，轴对称性的情况下的。
克尔黑洞的时空线元是：
可以看出比史瓦西时空的线元复杂很多倍。
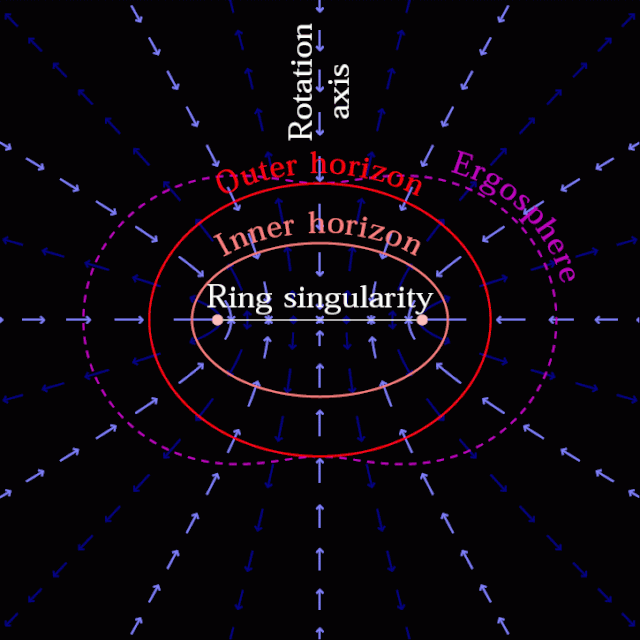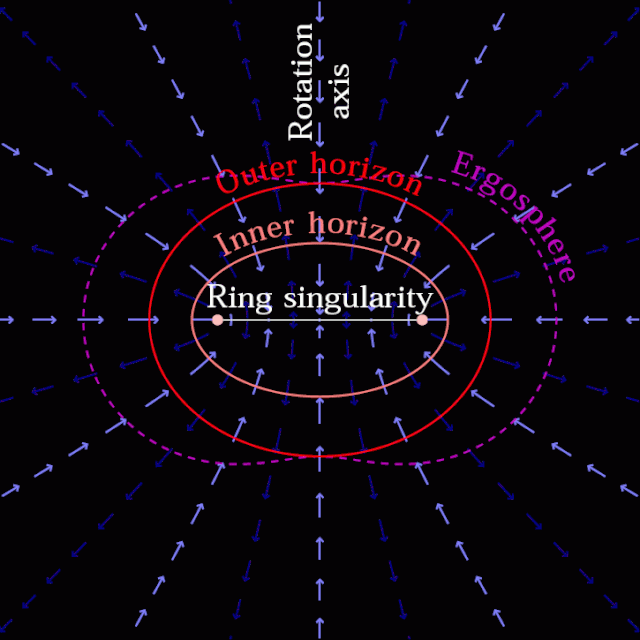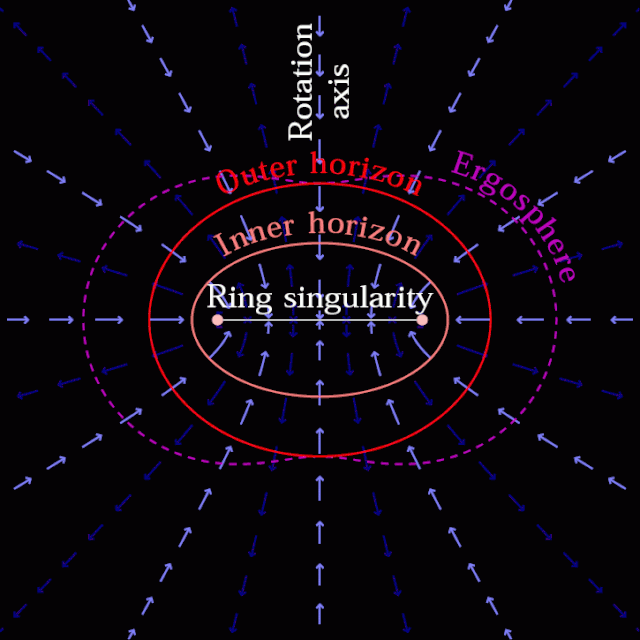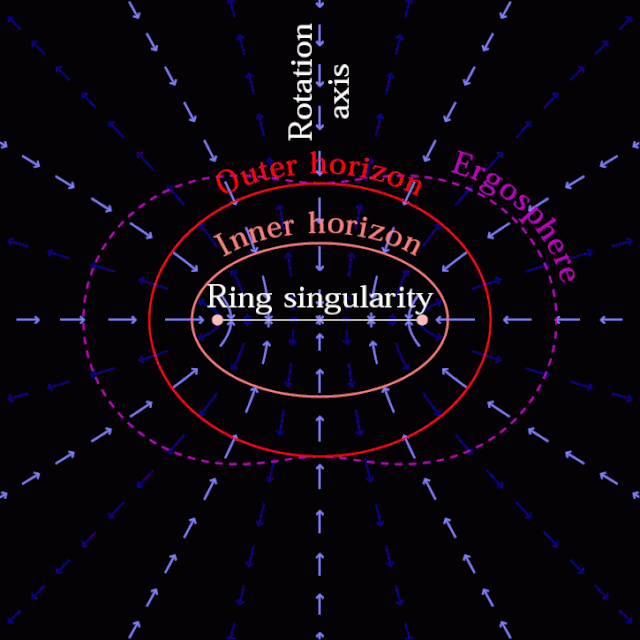
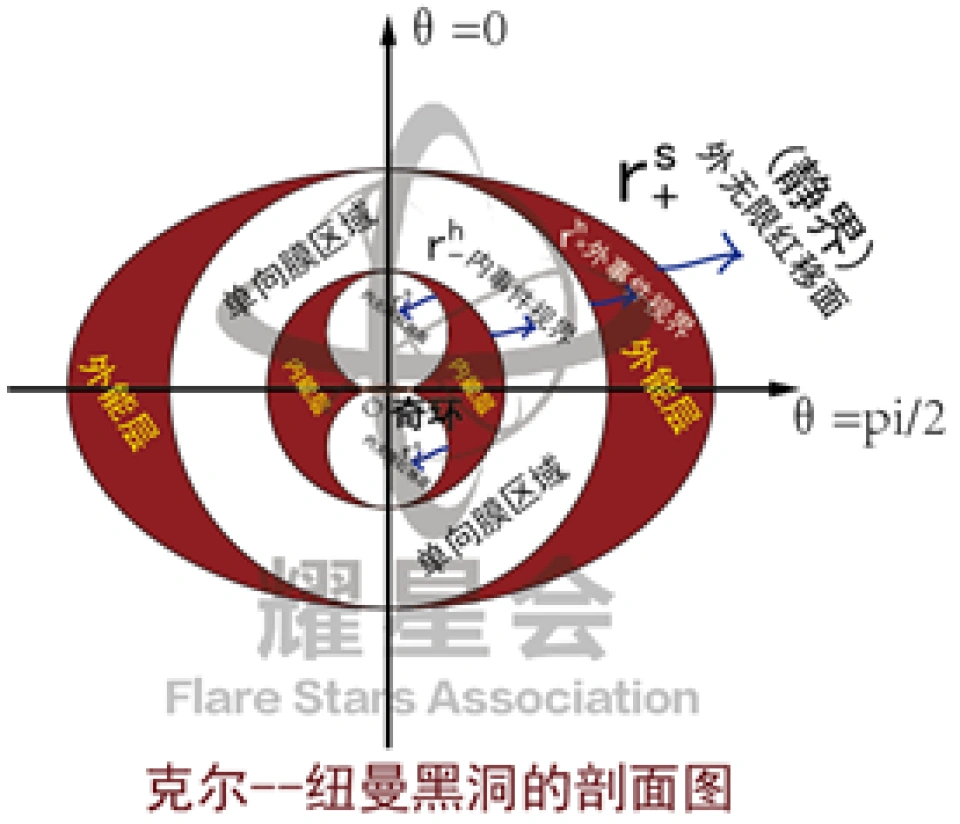
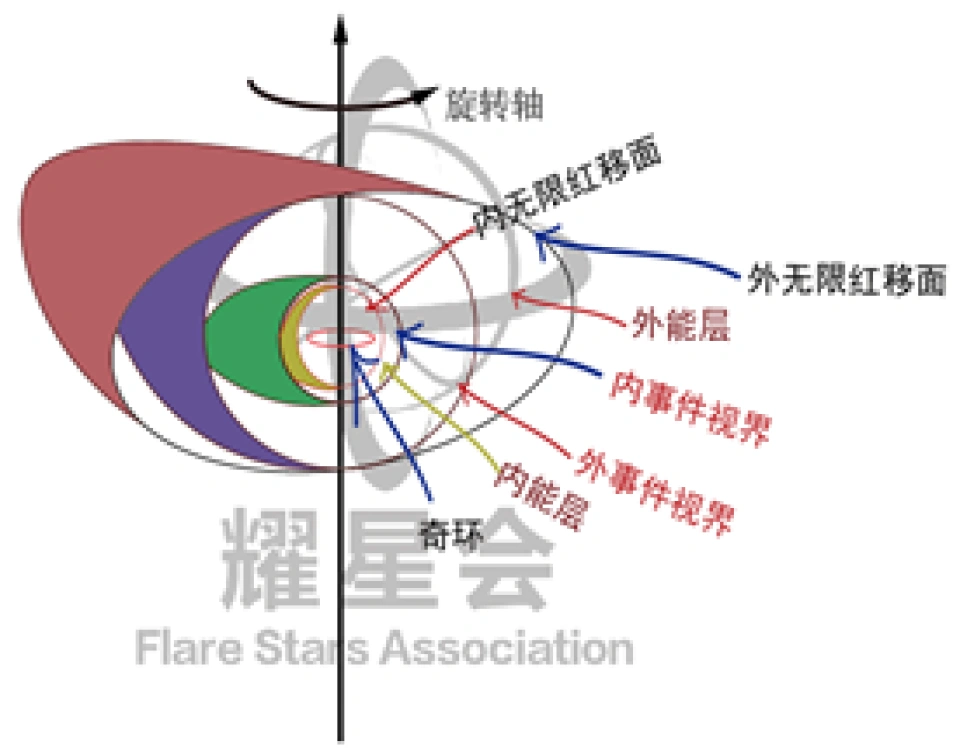
我们也可以得到克尔黑洞的时空结构图：
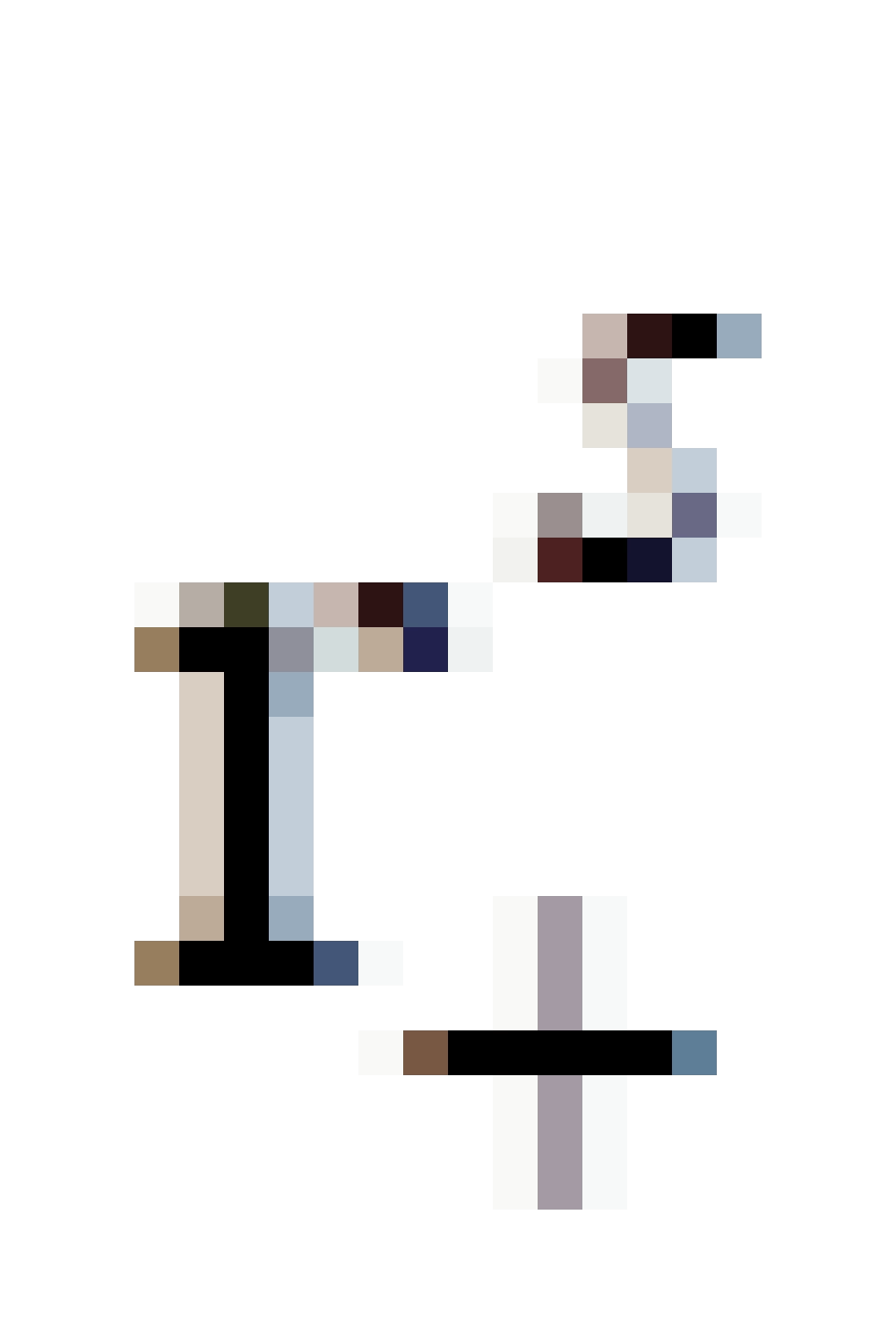是外无限红移面，在这个面的外面 
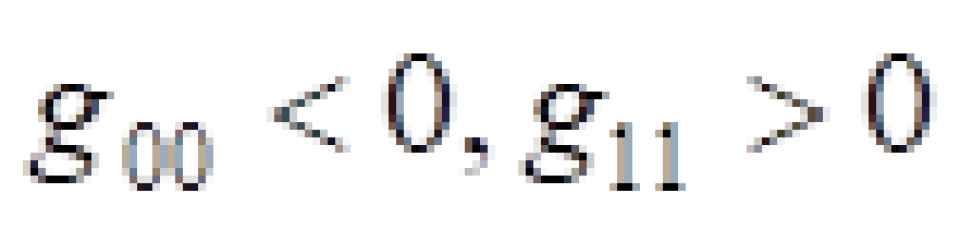，跟我们外部宇宙一样。
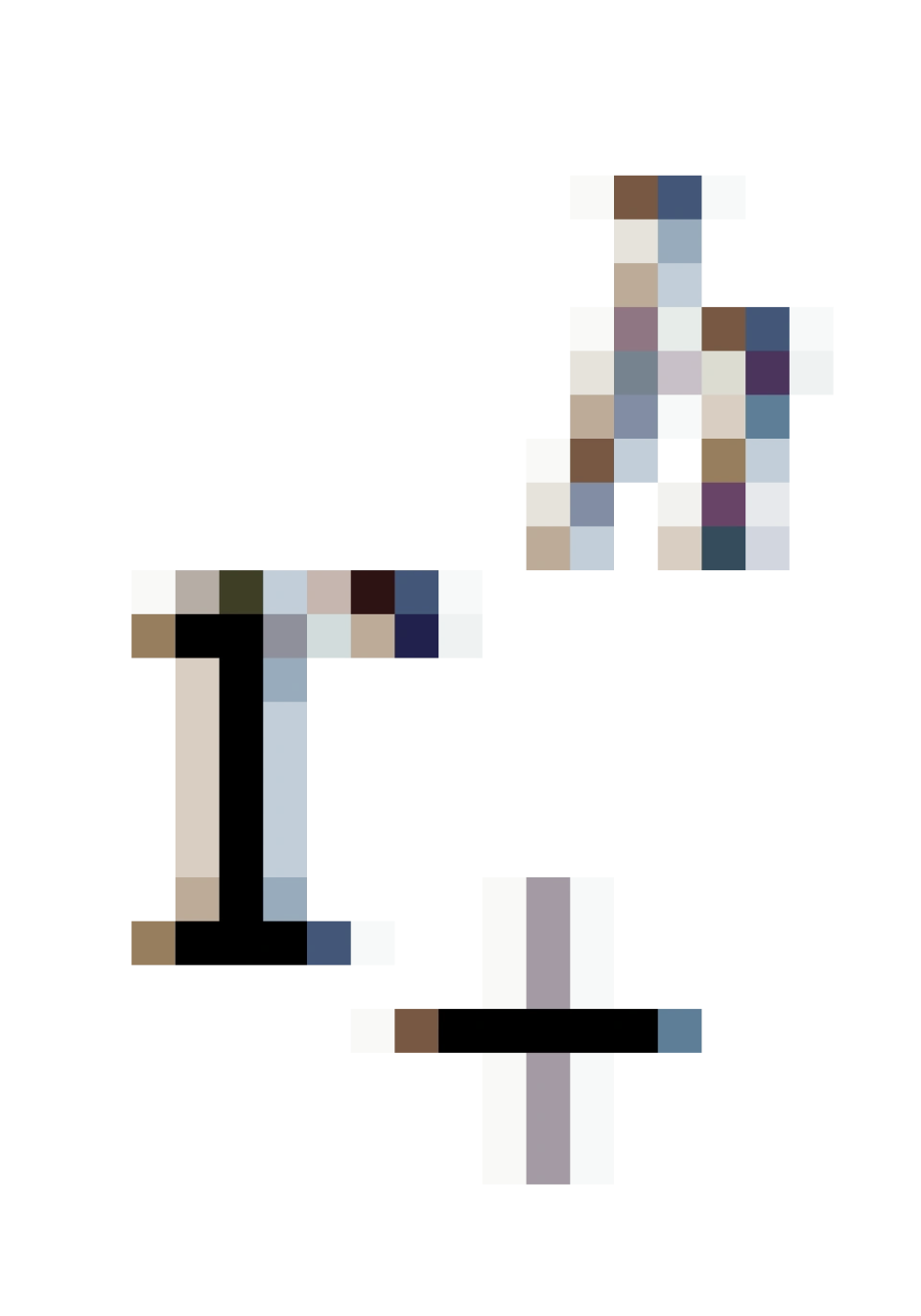是外视界，中间包裹的阴影区域是外能层，这个时空概念看不清楚，
因为在这里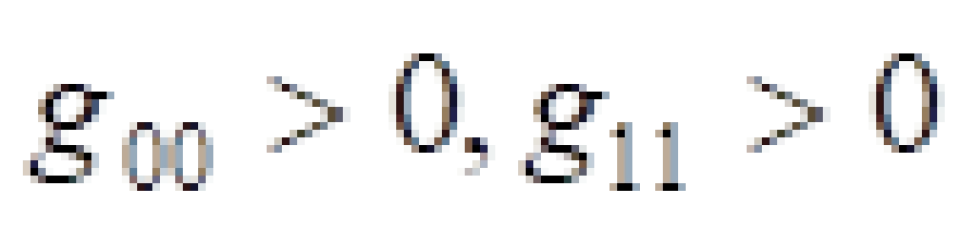
，所以根本就看不清楚哪个坐标代表的是时间，哪一个代表的是空间。上面我们说过，时空度规的一正三负正好对应着一个时间和三个空间，但是这里的时空度规对角元素都是正的。所以，这里的时空概念其实很混乱，我们根本弄不清楚。
时间和空间坐标不再是外部世界表述那样，它只允许类空世界线通过，因此任何物体都不可能在这里停留下去，并且在这个区域的物体会受到黑洞自转拖拽时空的影响，也就是所谓的时空漩涡，旋转方向就是黑洞自转的方向；这个被称之为时空拖拽现象。
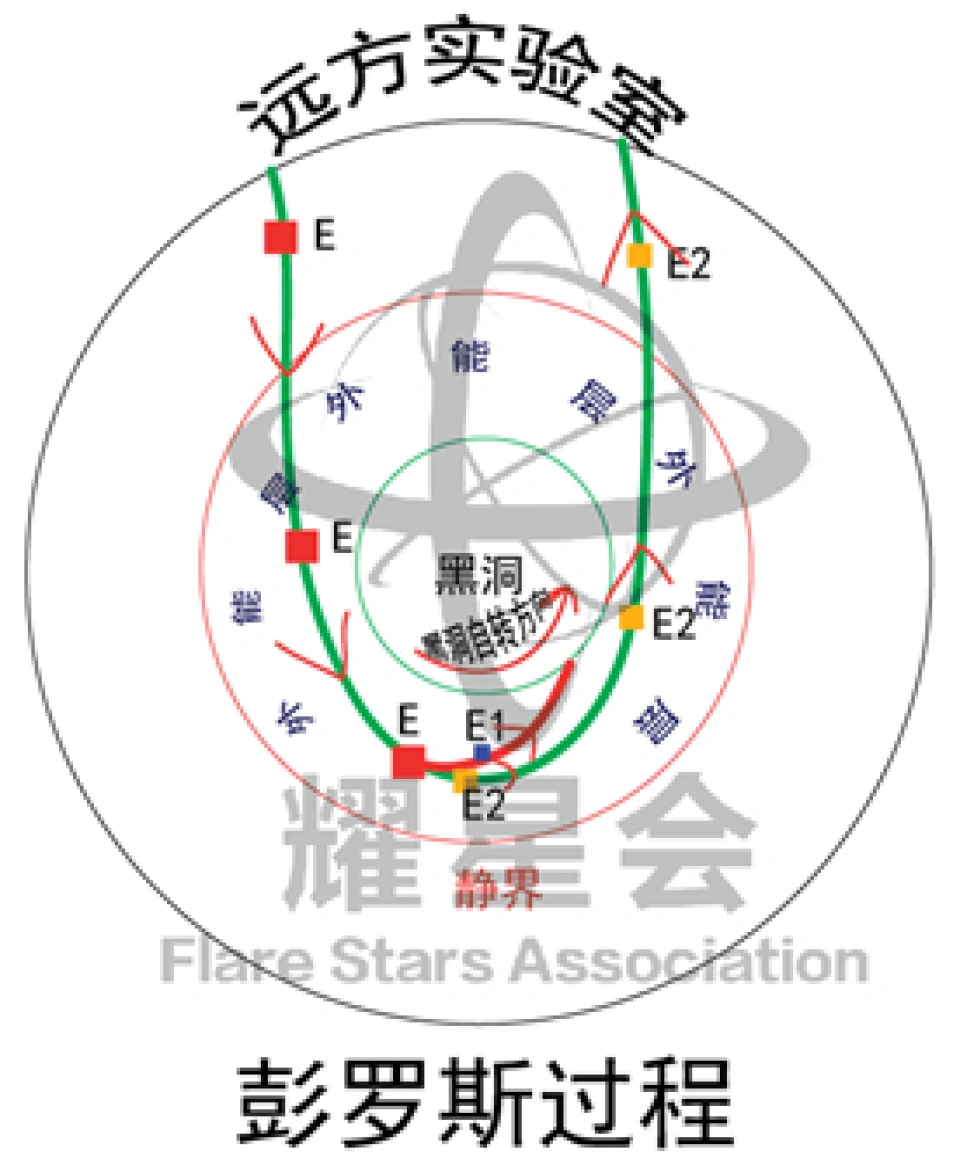
能层还有一个很好的物理现象，丢入一个物体，它会盗取黑洞的旋转能，从而以比如入射动能还要大的动能射出来，当然这个物体本身要抛弃一部分掉入黑洞。这个过程被称为彭罗斯过程。
如果以后在宇宙中发现这种克尔黑洞，人们就可以利用它来获取能源。这样会使黑洞自转速度越来越慢。
之所以会这样发生，是因为能层中存在着角动量为负的轨道。
我们都知道，在相对论的框架下，能量和动量其实是一家人。它们分别是一个叫做四维动量在时间和空间上的分量或者投影。
说到这里，我们简单温习一下相对论的四维矢量语言框架。
在相对论中定义时间和空间四矢量
其中，
。
我们之前说过，惯性参考系的变换下，有一个不属于坐标系变换的物理量一一时空间隔或者叫时空线元。记作：ds。并且根据这个定义了固有时间概念。
固有时间：
固有时间才是物体实际经历的时间，它跟坐标时间dt相差一个相对论因子γ。
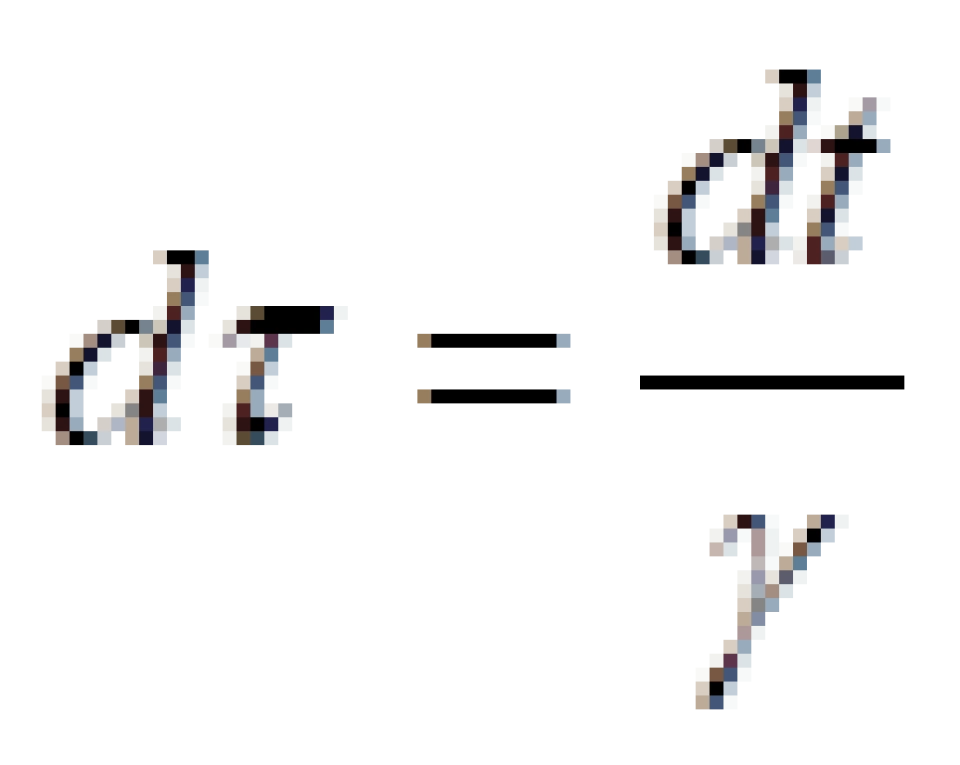有了固有时间就可以定义四维速度。很好定义，就是四维矢量
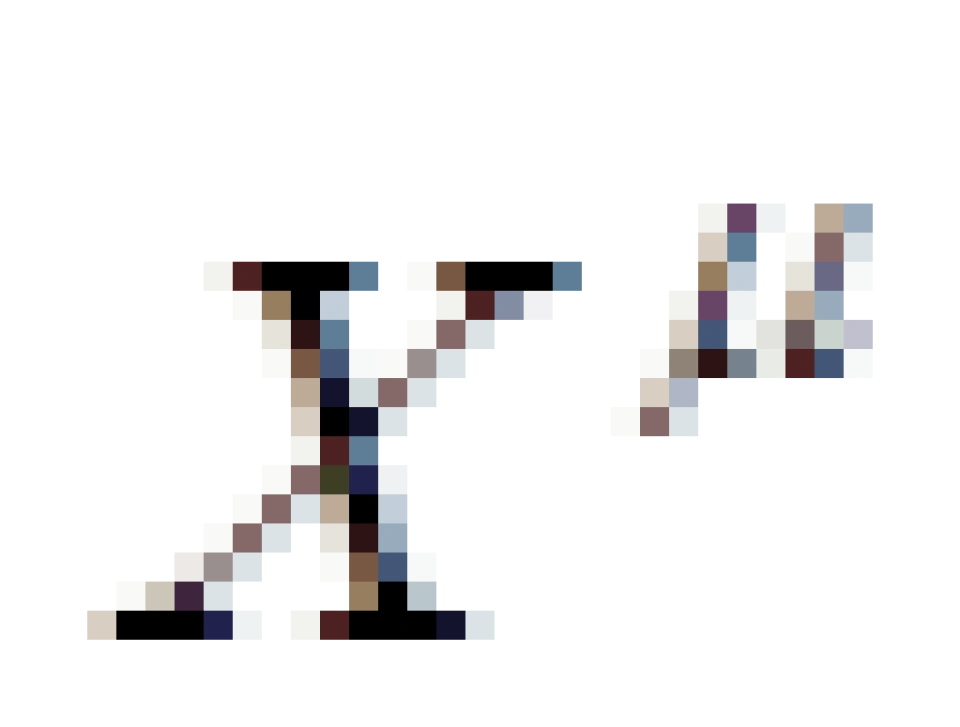对于固有时间 
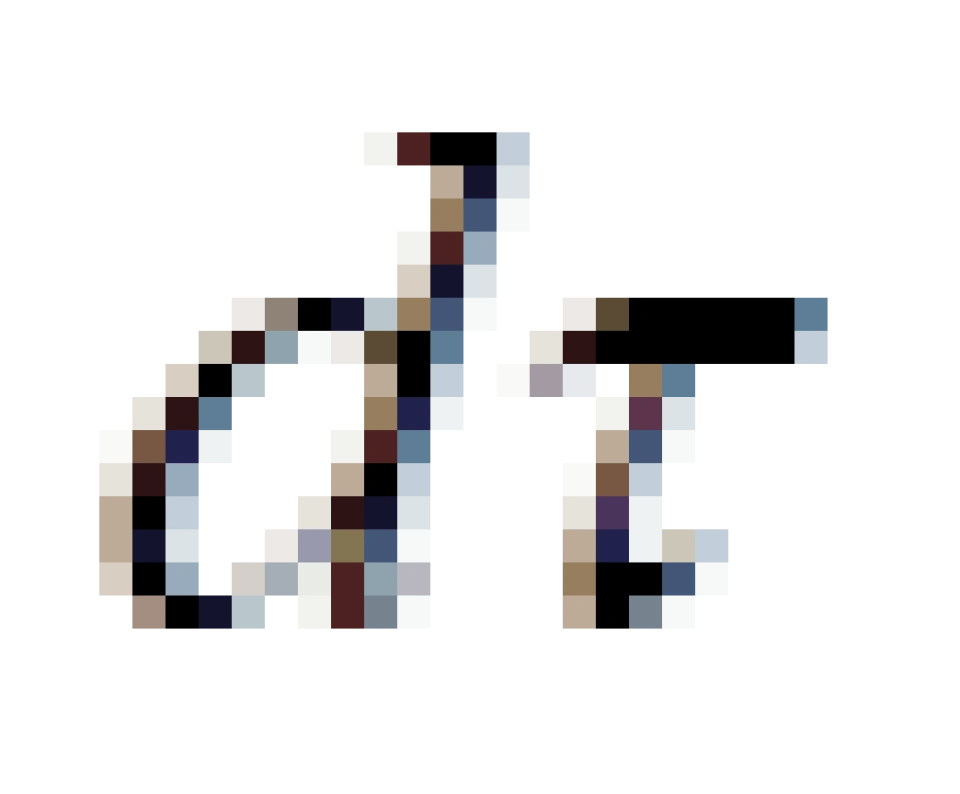的求导：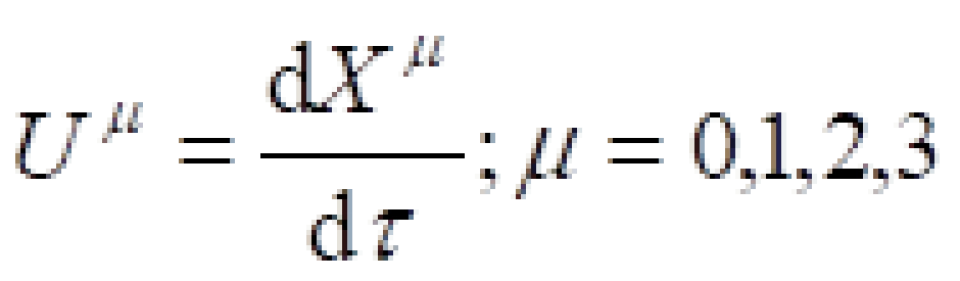
，这也是一个四维矢量。
其中：
这里的1其实就是光速c。
有了四维速度，我们就可以定义四维动量。其实就是质量乘以四维速度：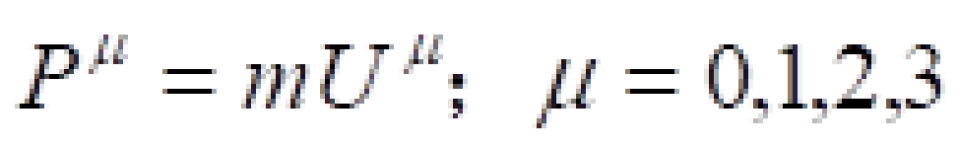
。
更进一步的，
而在相对论中，能量的定义为： 
到这里我们可以清楚看到时间上的分量或者投影，其实就是能量，空间部分就是动量。
，不难看出四维动量的第一个分量,跟能量其实是差一个光速c。不过，这都无伤大雅，不影响最终的结论。）
在相对论的框架下，能量和动量可以组合一个统一的四维动量去描述。
四维动量在时间轴上的投影定义为能量，在空间上的投影定义为三维动量。四维动量本身也是绝对的，但是它在空间轴或者时间轴上的投影则是相对的，依赖于坐标系的选择。
四维动量这些四维矢量的物理量不随坐标系的选择而变化，但是它们的分量会随坐标系的选择而变化。
因此，我们选择合适的坐标系，就可以去定义能量： 
这就是四维动量在时间坐标轴/时间坐标曲线上的投影。
在弯曲时空中，时间坐标曲线一定是类时的，因为只有这样我们才可以走。也就是这个时间坐标曲线上每一点的切矢量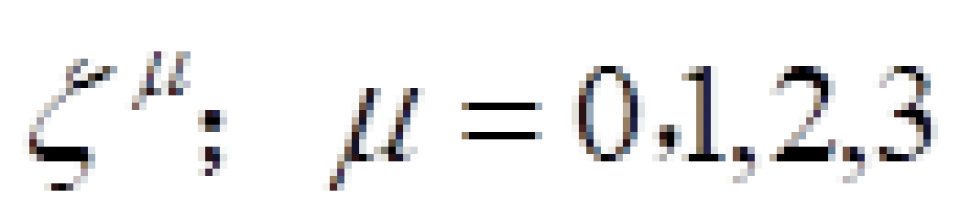
一定满足：
由于
是时间坐标曲线上每一点的切矢量。因此， 
所以有： 
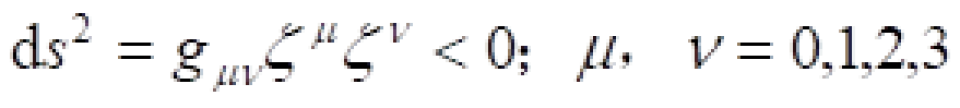
不过呢，在能层里，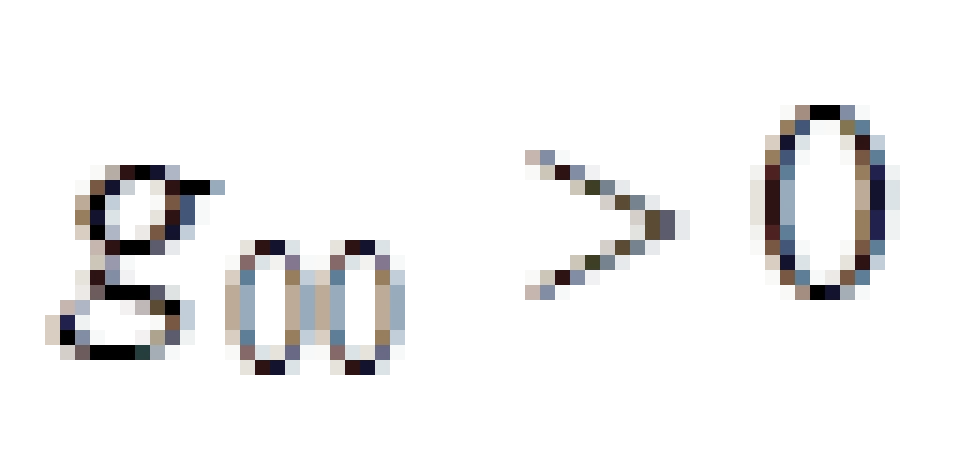 
。这也就是告诉我们时间坐标曲线在这个能层里是类空曲线。能量的定义是四维动量在这个时间坐标曲线上的投影，如果时间坐标曲线是类时的，也就是在外部正常时空，那么能量一定是正的；如果是类空的，那么能量可能是正的，也可能是负的。所以在能层里除去正能量轨道之外，还存在负能量轨道。这些负能量轨道都是角动量为负的轨道，也就是跟黑洞的自转方向相反的轨道。
因此，如果一个无穷远处能量为E的物体在不受任何外力的作用下飞向黑洞，将沿着测地线（弯曲时空中的直线）运动。那么当它进入能层之后分裂成两块，其中一块所具有的能量为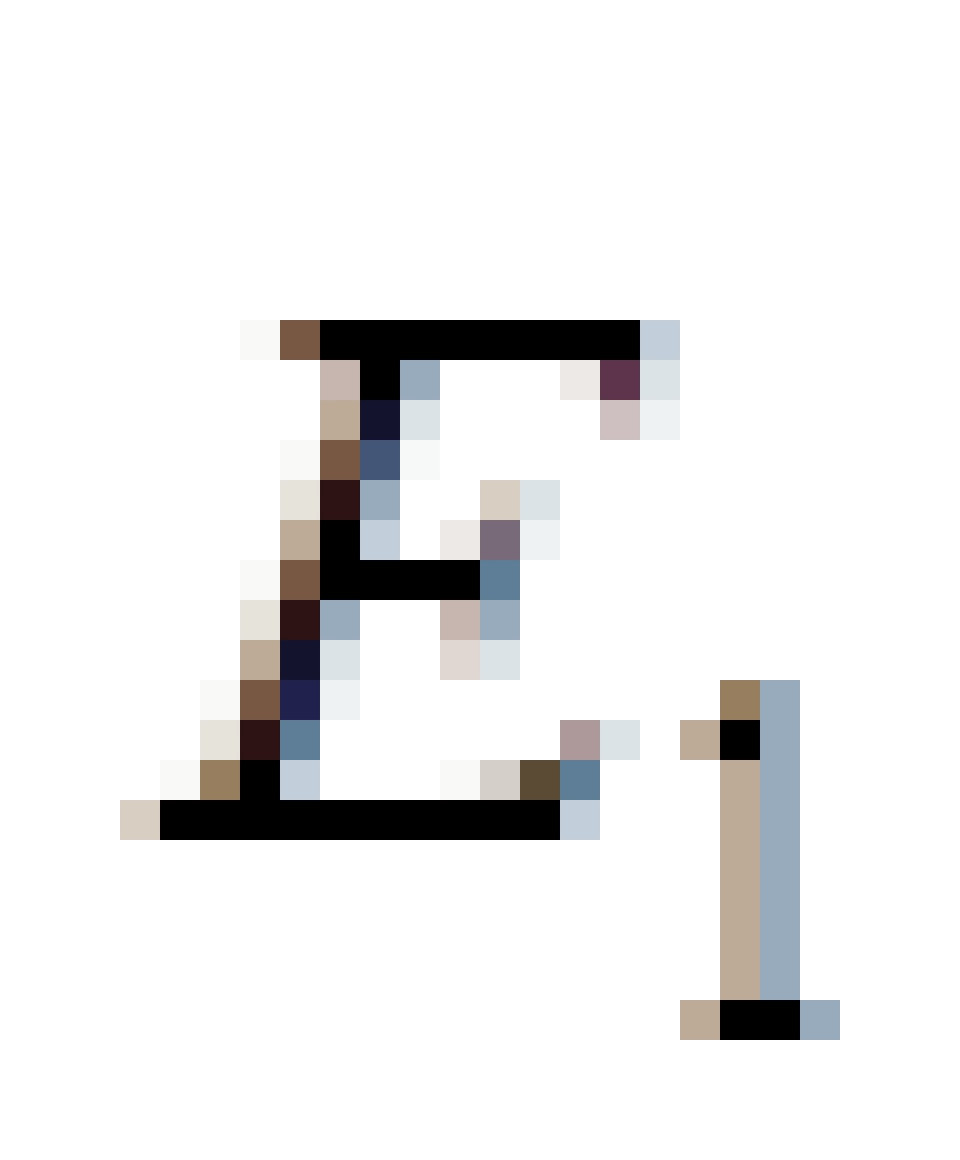 
的碎片沿着负能量轨道进入黑洞内部，而另一块所具有的能量为
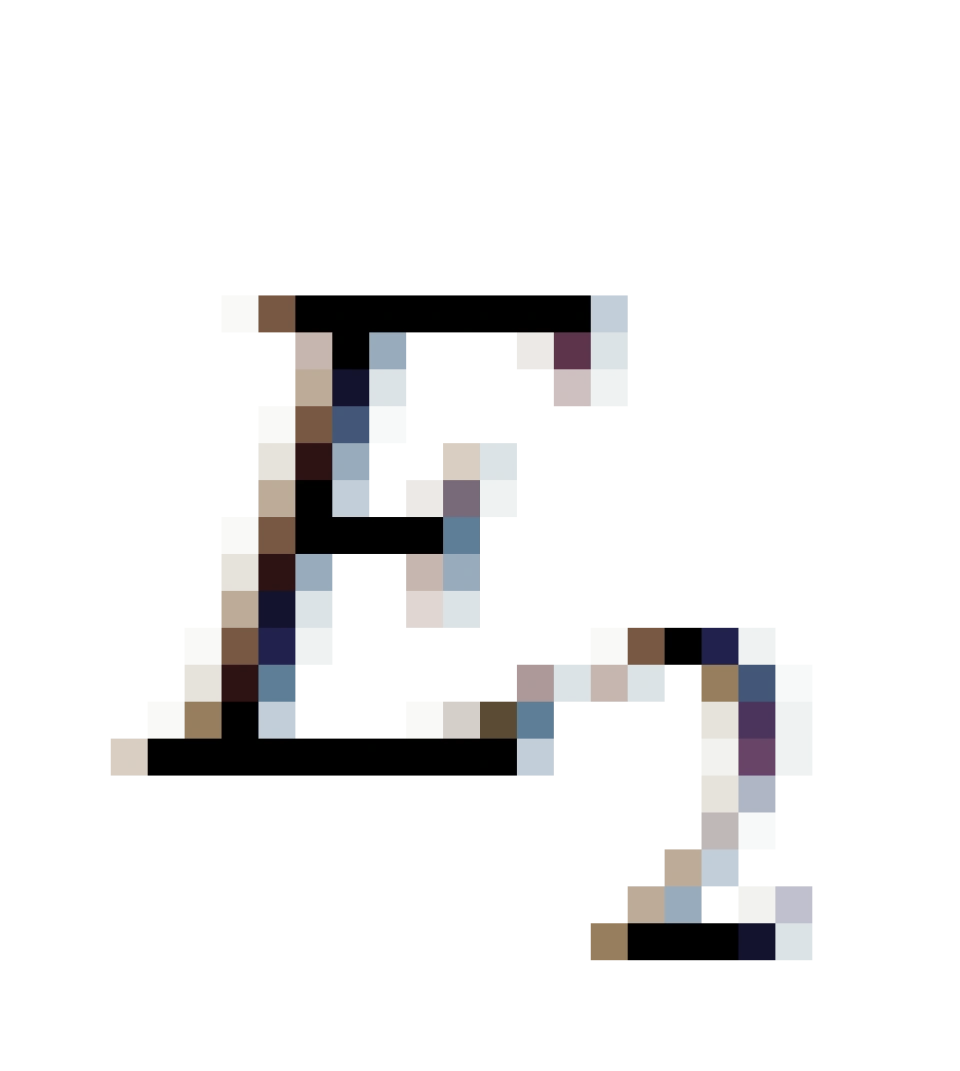的碎片能够逃出来。
由于能量守恒，则有：
但是，由于进入黑洞的那块碎片，它是沿着负能绕轨道进入的，所以它具有的能量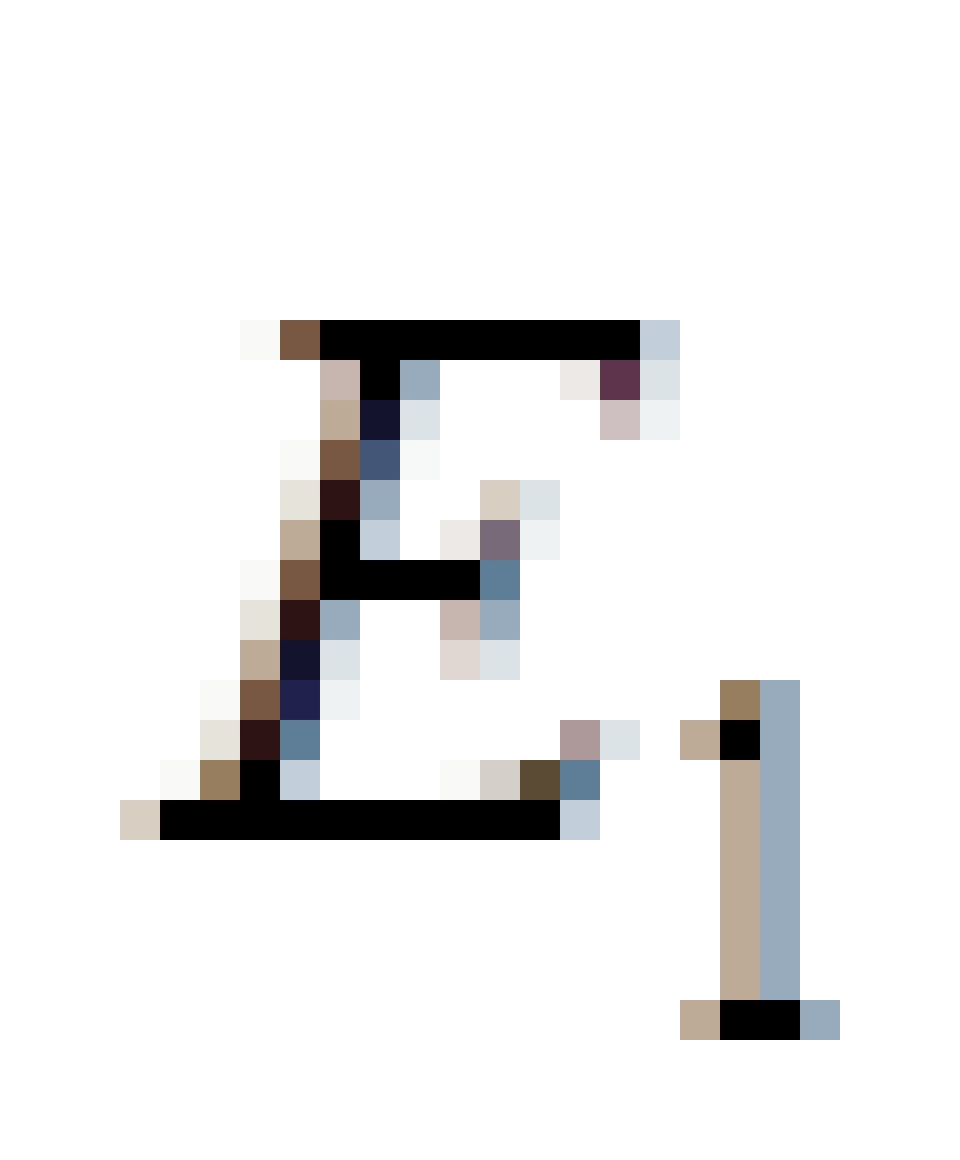 
是小于0的。这将导致
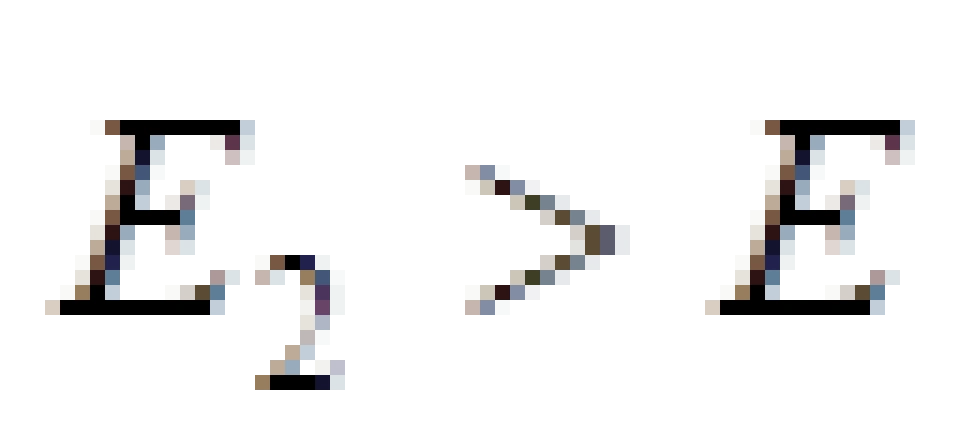,这意味着，在无穷远处实验室的观察者得出的结论是，物体的出射能量大于入射能量；也就是说他能用这种方法从黑洞的能层中提取了能量，这一效应就被称之为彭罗斯过程。
另外，由于进入黑洞内部的物体是沿着负能量轨道进入的，所以说这个物体具有的角动量是负的。而这个负的将由黑洞的角动量去偿还，所以黑洞会越转越慢。
不过值得注意的是，如果有一个观察者也在能层之内，那么它无论观察哪一个碎片，所具有的能量都是正的。但是对于无穷远处实验室的观察者来看，沿着负能量轨道进入黑洞内部的碎片就是负的。能量不是一个坐标不变量，但是它是一个守恒，所以黑洞偿还了这些东西。
彭罗斯过程的微观版本就是米纳斯超辐射，进入黑洞的物体是具有量子效应的。也可能是一束激光，一束光或者是任何带电粒子，任何粒子。如果是带电粒子，那么黑洞将会损失电磁能量。
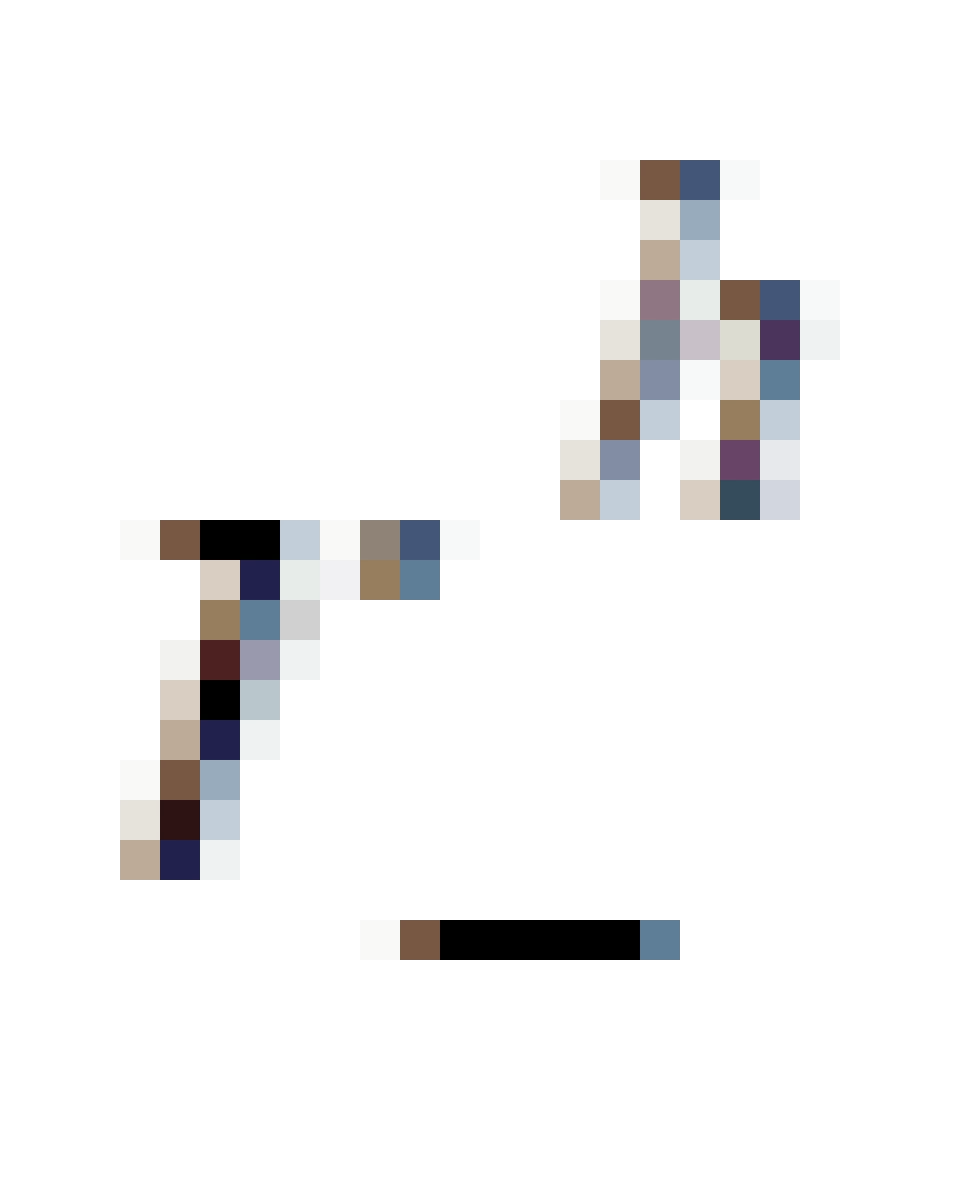是内视界，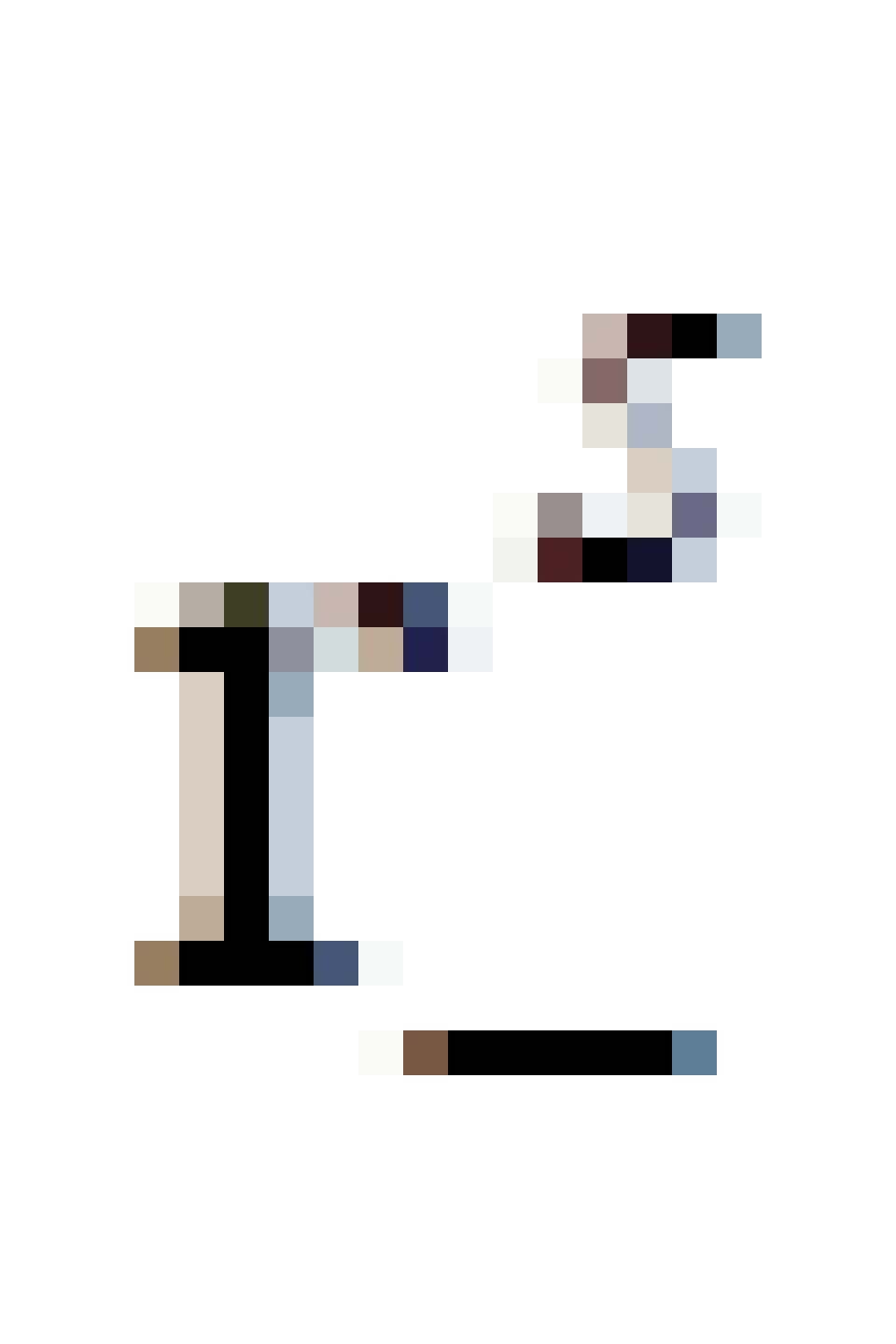
是内无限红移面，这两个之间包裹的区域叫做内能层，这里的时空概念同样也看不清楚。
内外视界包裹的区域是单向膜区，因为在这里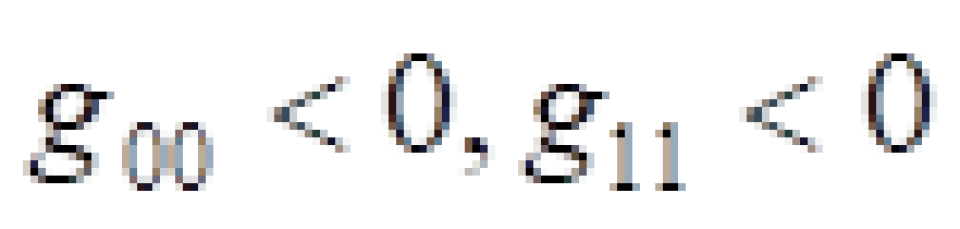
，时间坐标充当空间的角色而空间坐标充当时间的角色。所以说要不可避免的撞到内视界中，就如同我们上面介绍史瓦西黑洞内部情况一样。在那里，物体不可避免的撞向奇点。回在这里，物体进入了就不可能回到克尔黑洞外面。
而图中的“8”字形里面也就是内无限红移面之内的区域，这里的时间和空间概念跟黑洞外面的时间和空间概念一样。这意味着这个区域有可能跟我们外部的宇宙一样。
与史瓦西黑洞不同的，克尔黑洞的奇点其实是一个环。
由于奇环是在内无限红移面所包裹的区域之内，而那里又和外部的宇宙一样是正常的时空概念，并且这里也不是单向膜区，因此，这里的物体可以很自由自在的在这里运动。
在这里时间坐标t充当时间的角色，而是空间坐标r则继续充当空间的角色。
克尔黑洞奇环/奇异性，也就是r=0就变成一个等空间面。这个面跟时间方向平行。这种奇异性被称为类时奇异性，所以克尔黑洞奇环被称为类时奇点。但是奇环具有强大的斥力，物体不会撞到奇环，但是有可能从中间穿过去。不过，大部分人认为这个区域往往是不稳定的。
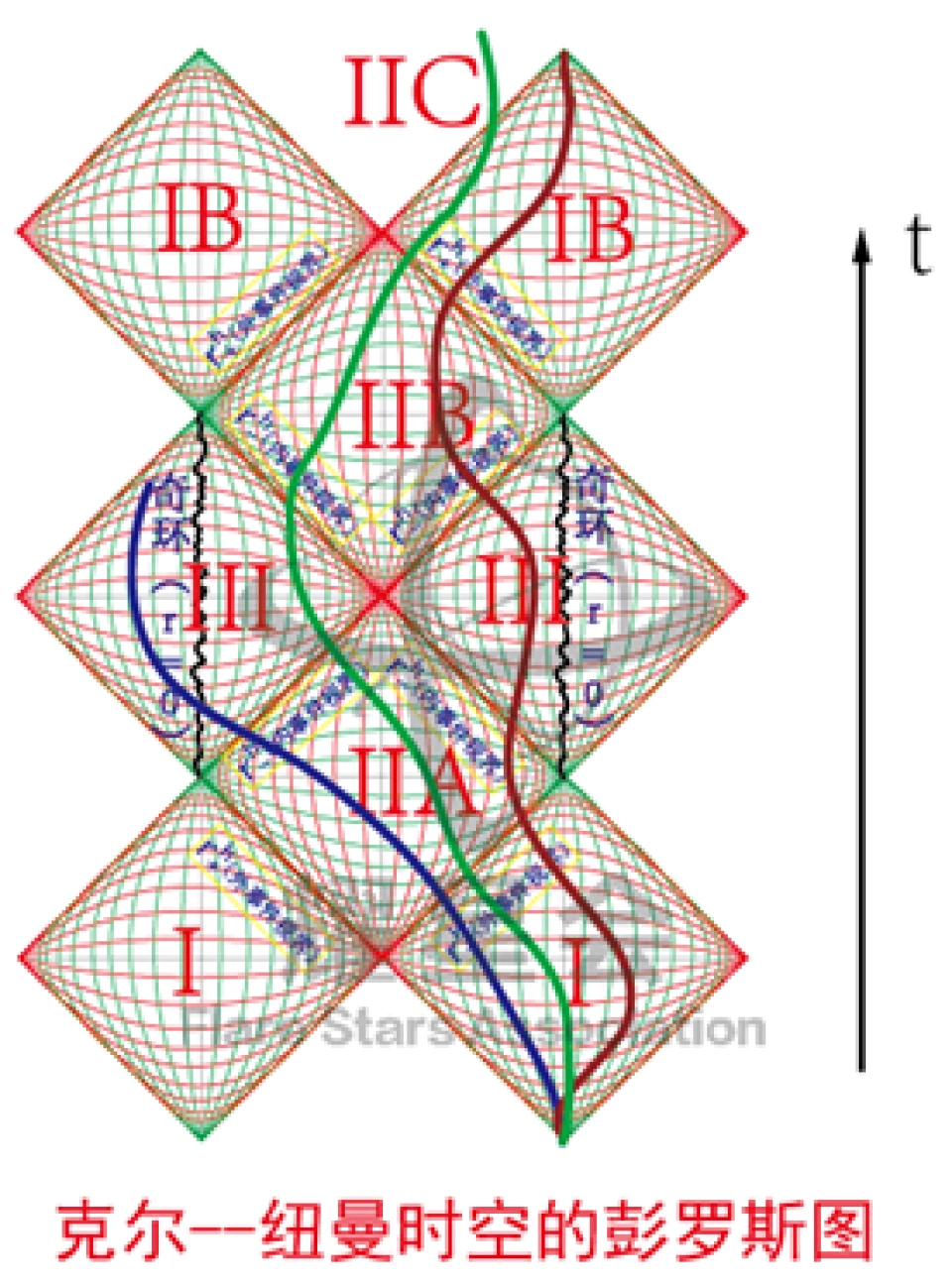
现在我们来看一下克尔黑洞的彭罗斯图就一切都明白了。
r=0就是奇环处，图中几个穿插的线就是世界线。
I区是外部的宇宙，也就是我们所生活的宇宙。II是单向膜区，而III则是内视界包裹的时空区域。这里的时空奇点或者叫奇环跟史瓦西的不同，它是类时的，因此是允许物体通过它的。
蓝色世界线将穿过奇环，进入一个反引力宇宙，至于这里到底是什么地方，目前也不知道。
红色世界线和绿色世界线将穿过奇环，进入一个正常的宇宙。克尔黑洞的彭罗斯图理论上是上下无限延伸的，仔细看图沿着时间方向走，看好等时间线和等空间线，就可以看懂每个区域代表什么。
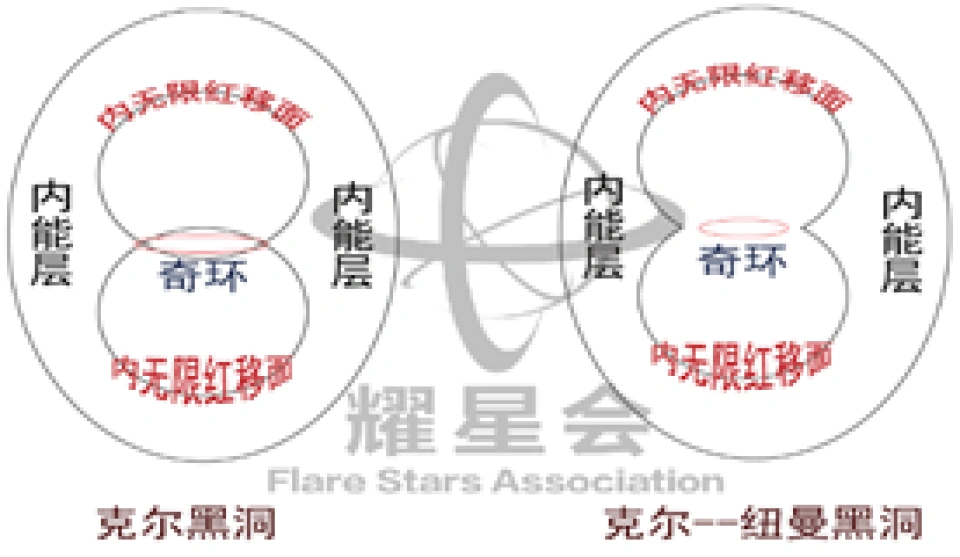
对于第3种普遍的情况，克尔一一纽曼度规，跟这个差不多。但是最大的区别在于奇环与内能层的关系。
图中左边是克尔黑洞，右边是克尔一一纽曼黑洞。两个黑洞的黑洞结构只有这方面不同，其它的都差不多。
不过这两种改造而来的虫洞即使允许类时曲线通过，也是不稳定的。它会在某种量子真空微扰作用，跟内视界重合，从而从只允许通过类时世界线变成只允许通过类光世界线。
更不要说穿过它需要面临巨大的引力。充满了很多危险。你要穿过黑洞的事件视界，到达奇点或者奇环附近。这已经是九死一生了。
以上这些还只是在广义相对论框架之下，如果考虑热力学和量子力学呢？这个时候，黑洞又有哪些有趣的性质呢？
下期再会。
参考文献：
《广义相对论基本》，赵峥，刘文彪
《广义相对论》，刘辽，赵峥
《黑洞的热性质与时空奇异性–零曲面附近的量子效应》，赵峥
《黑洞与弯曲的时空》，赵峥
《微分几何入门与广义相对论》上中下册，梁灿彬
【本文为耀星会的原创作品，未经允许，禁止盗用、转载、篡改文章，否则耀星会将追究版权责任。】
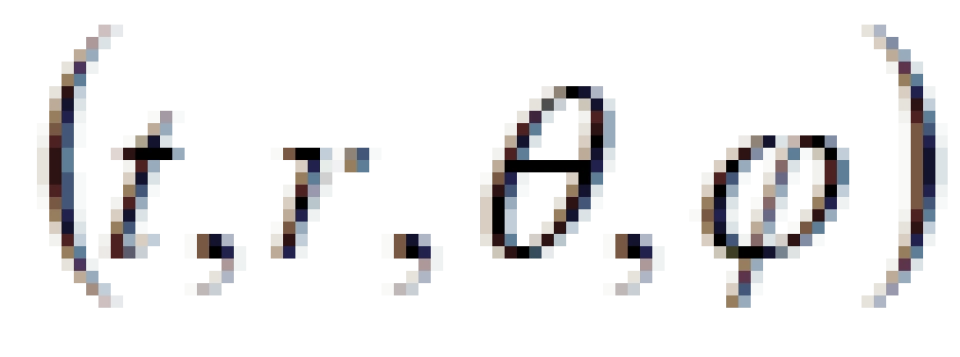
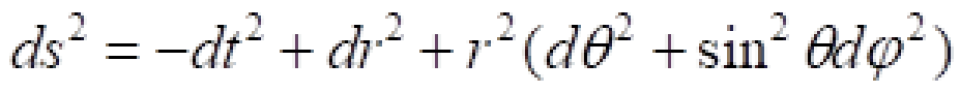
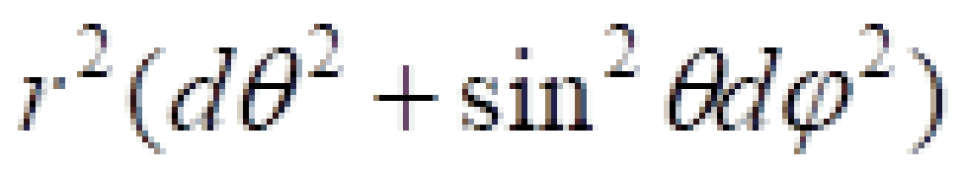
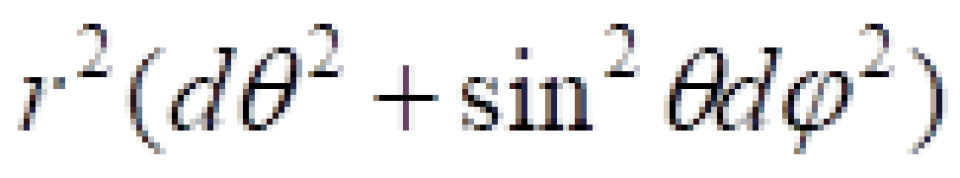
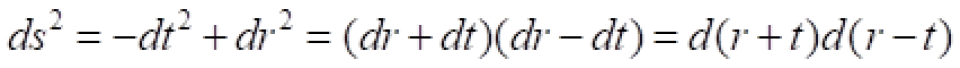
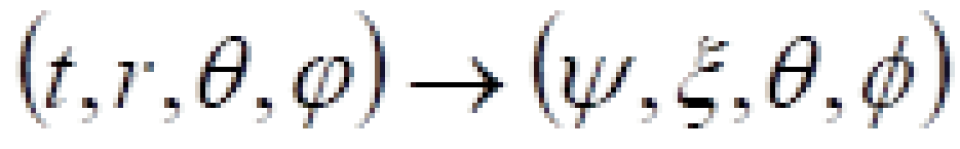
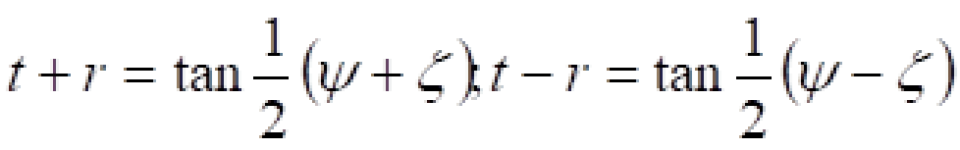
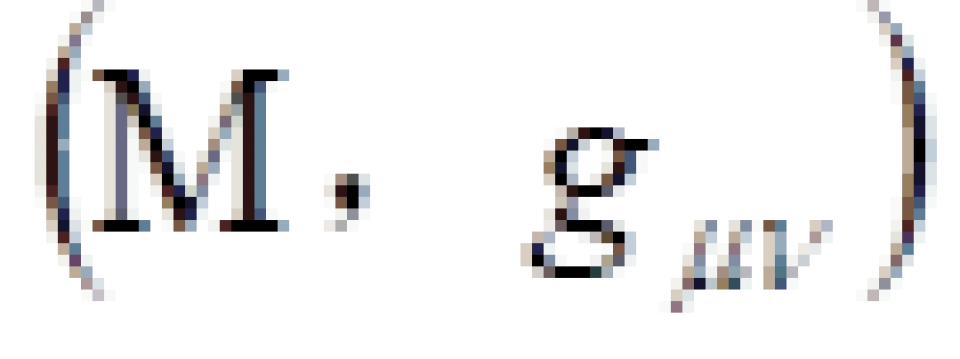
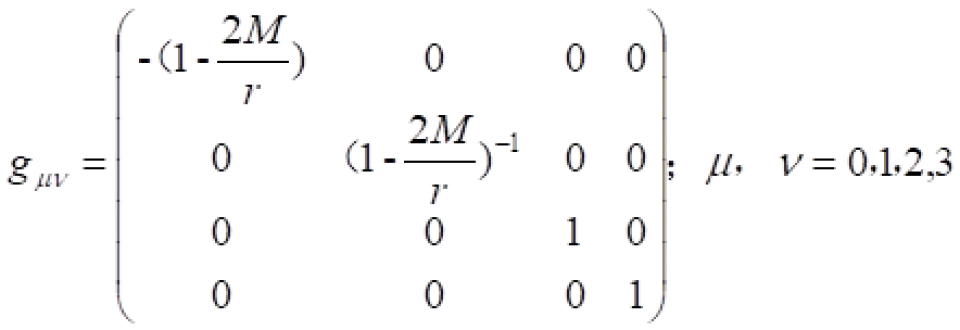
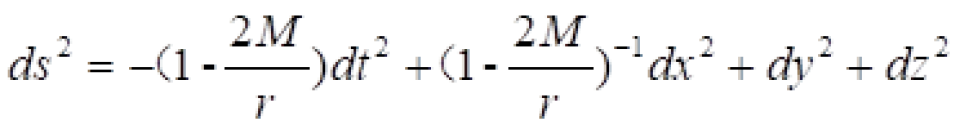
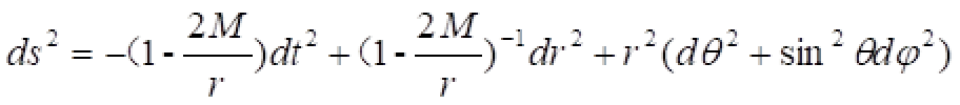
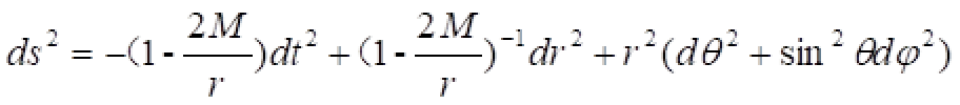
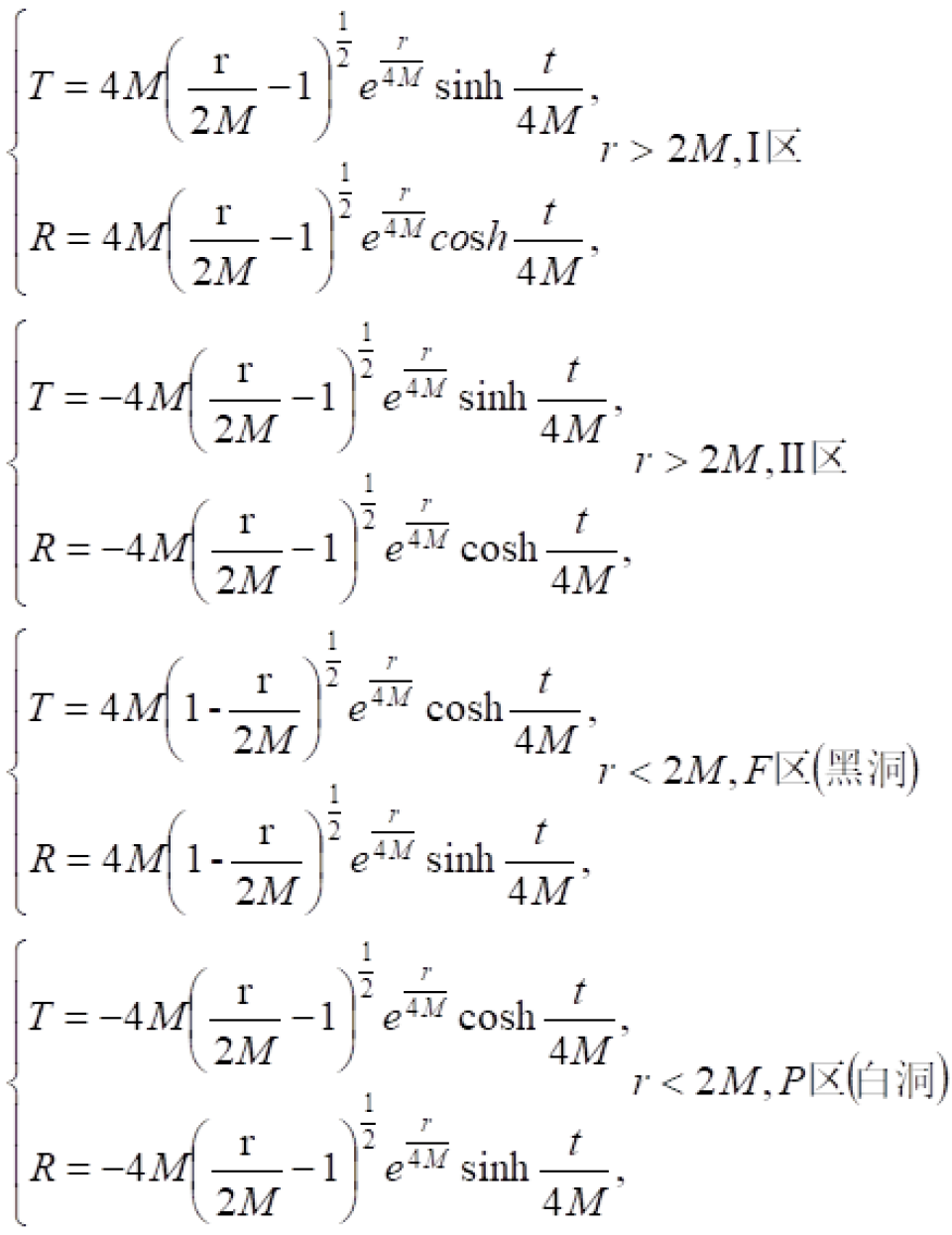
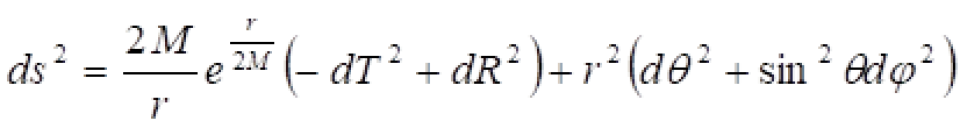
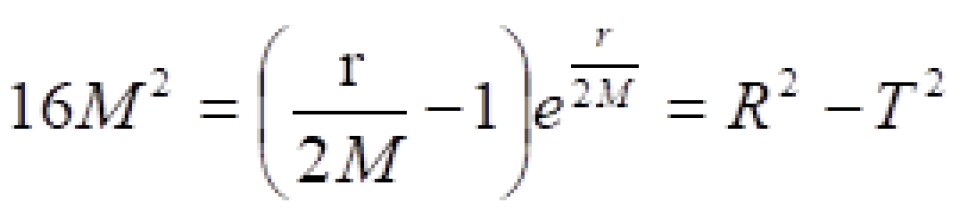
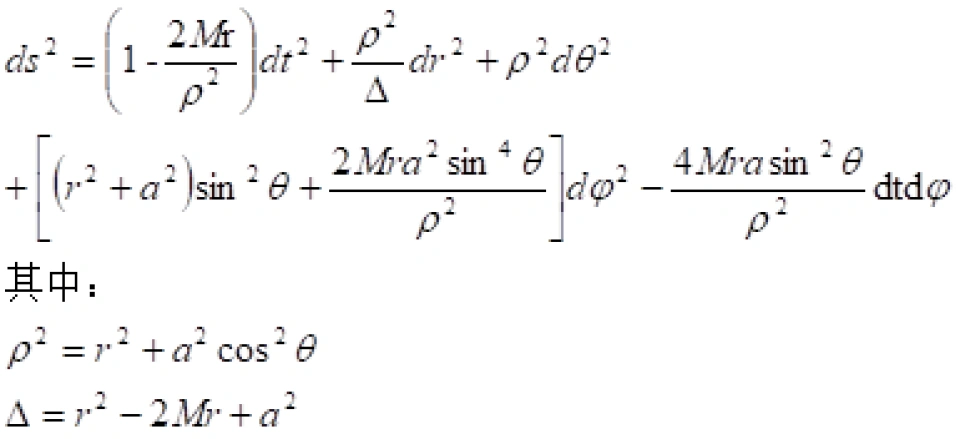
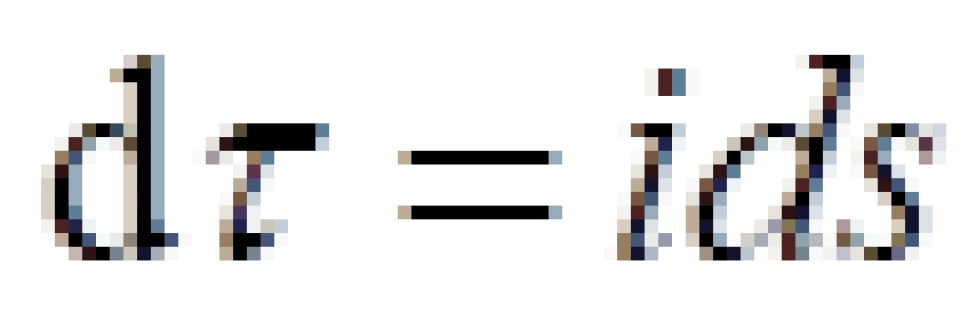
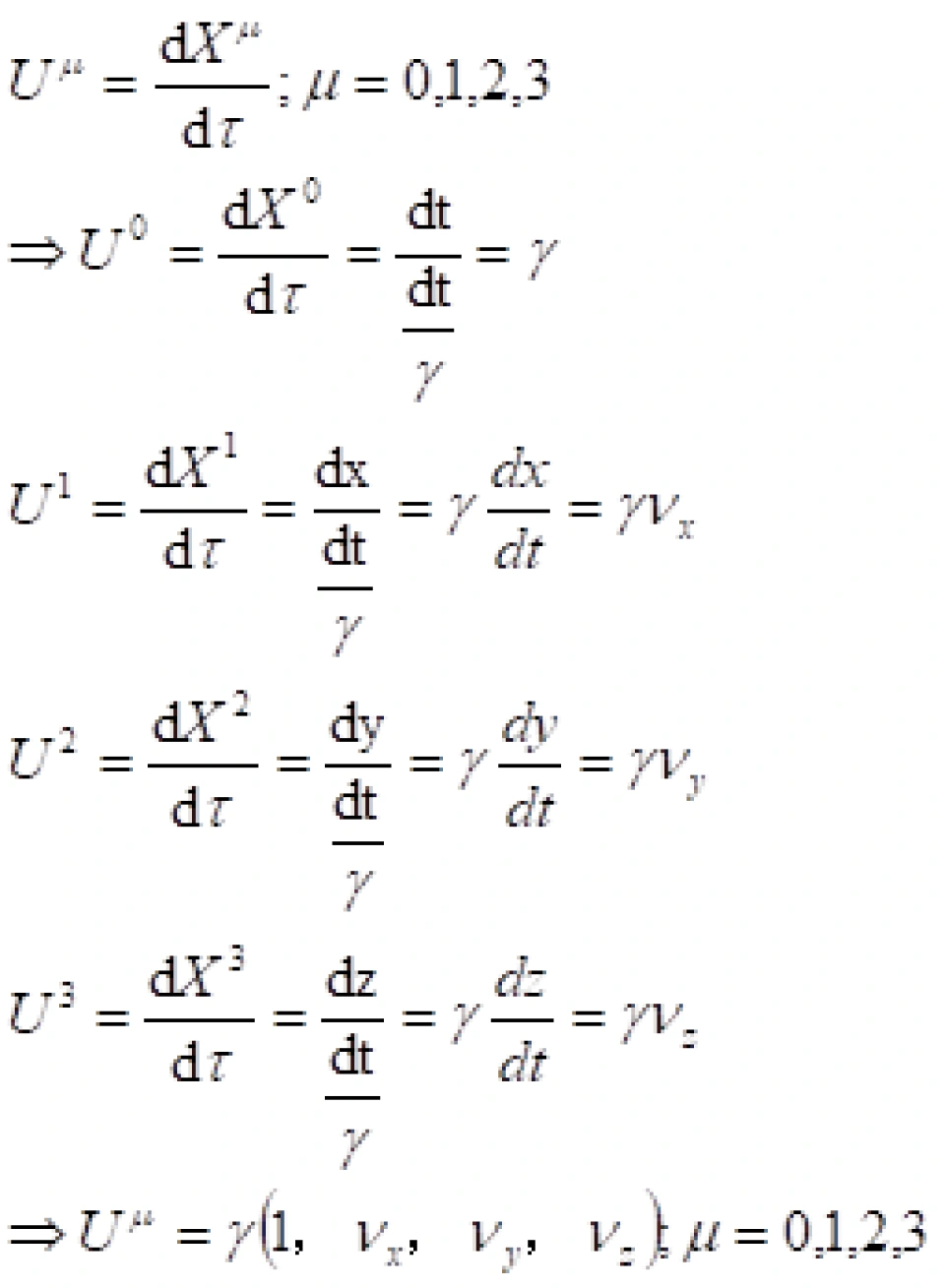
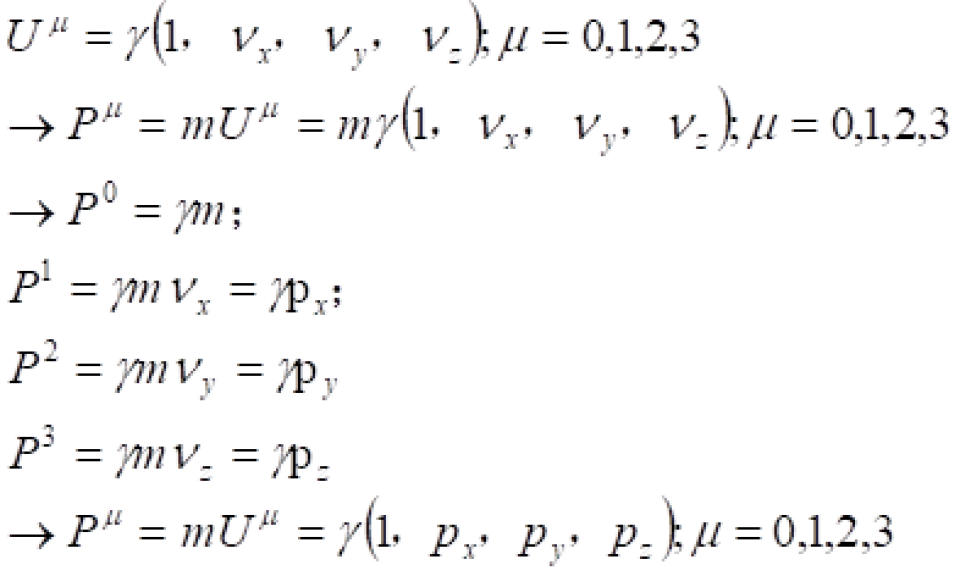
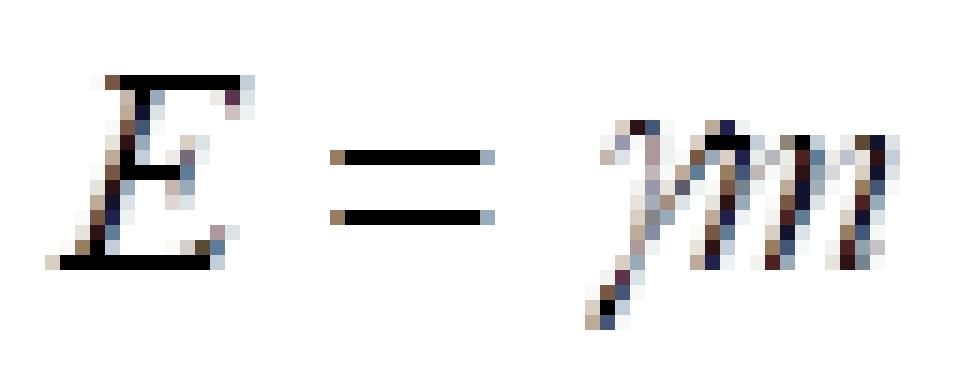
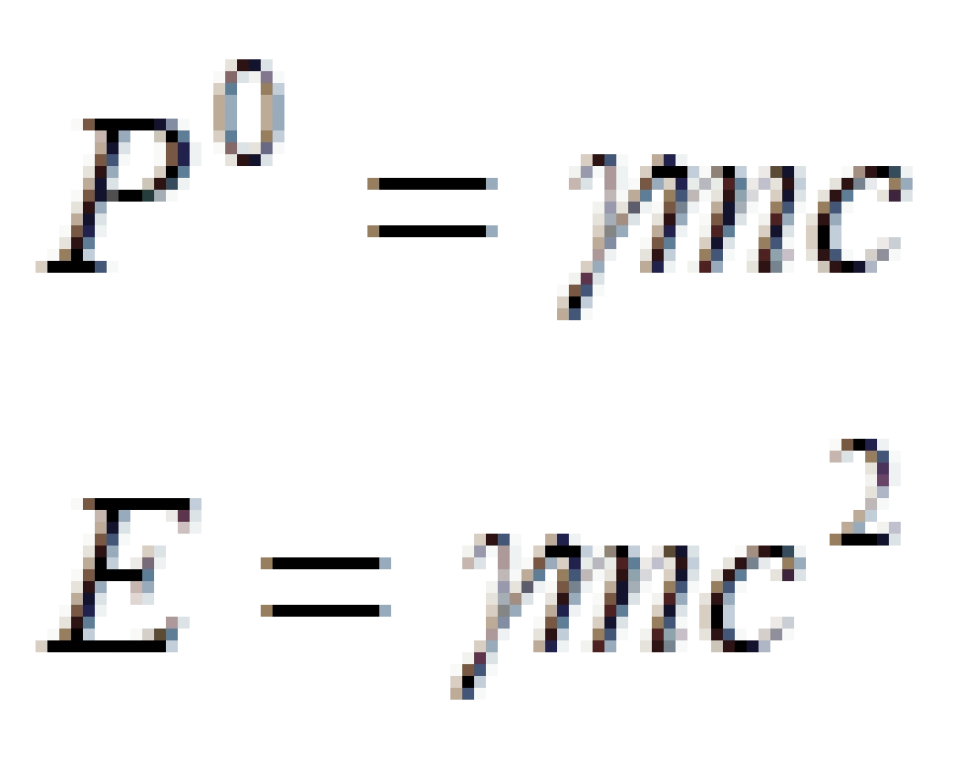
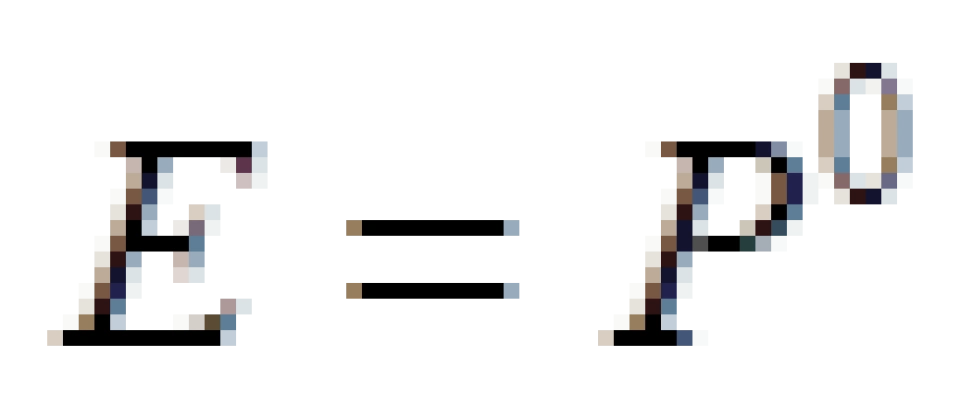
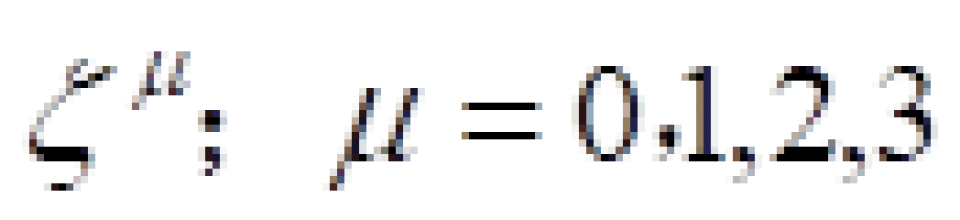
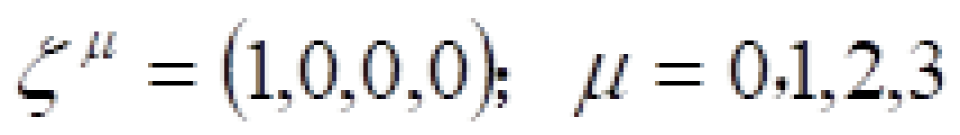
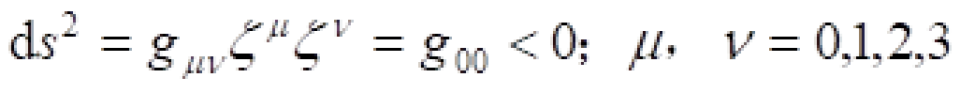
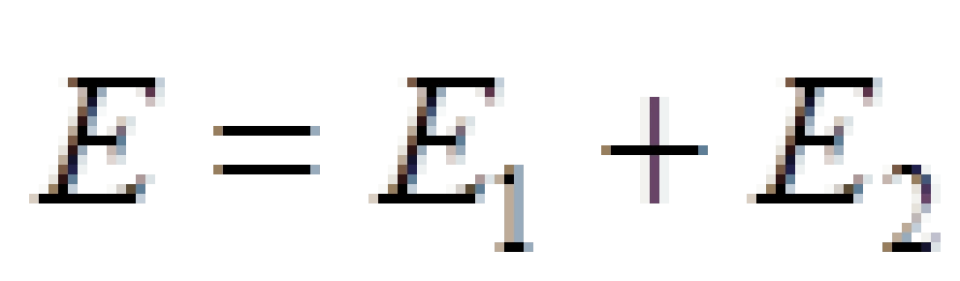
很用心了 [s-85]