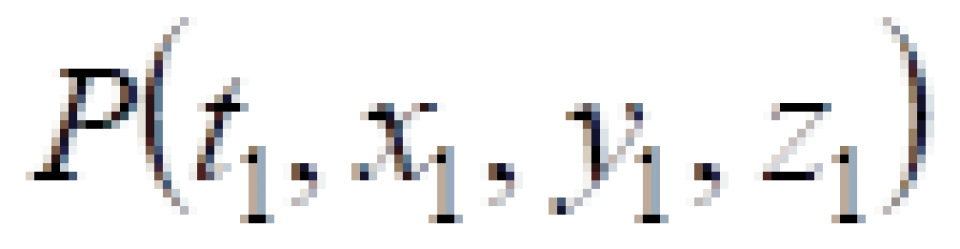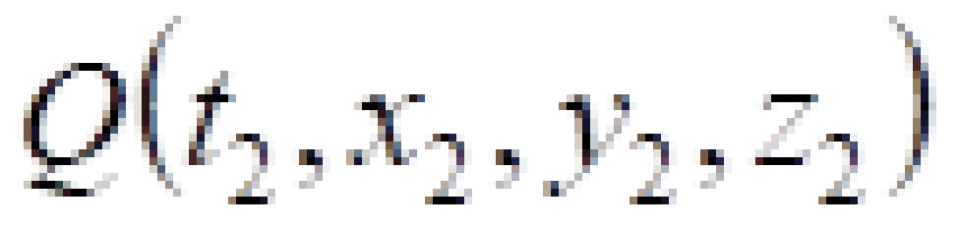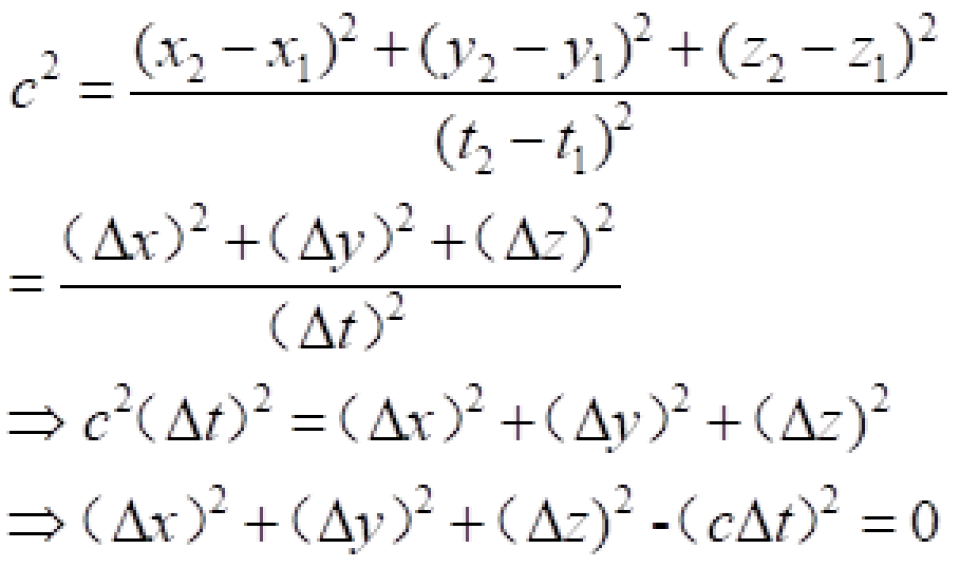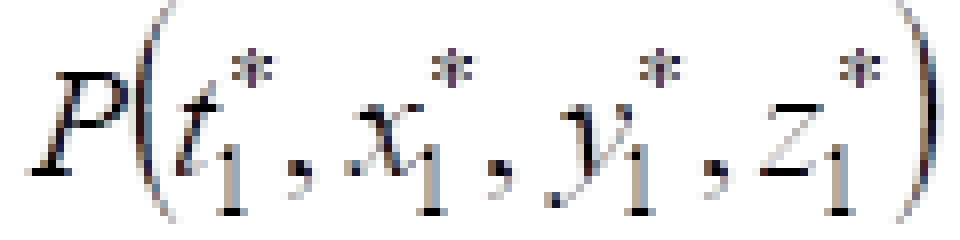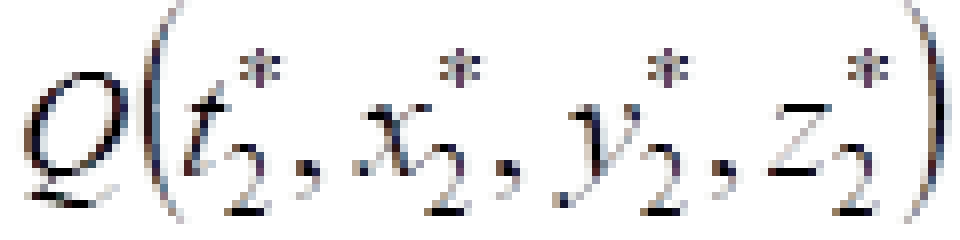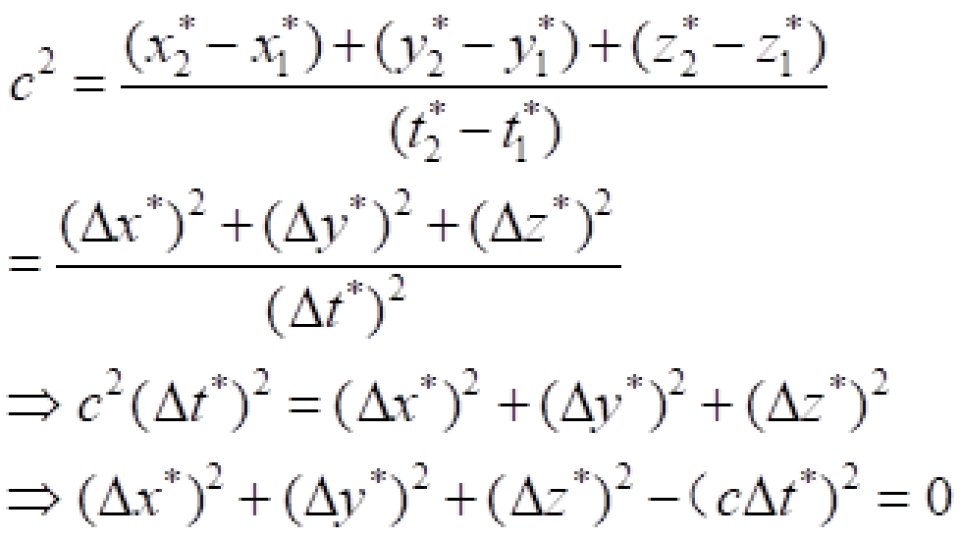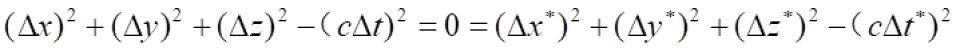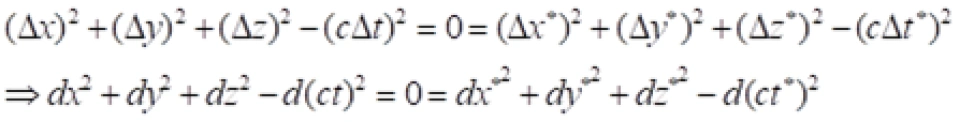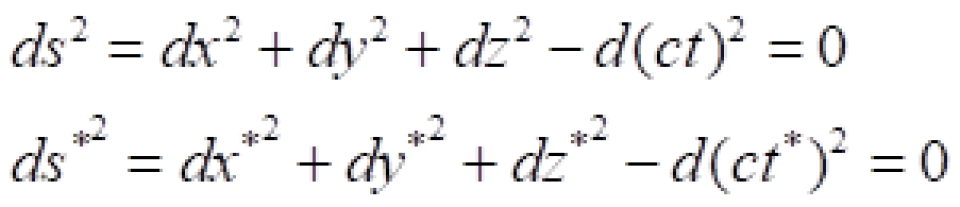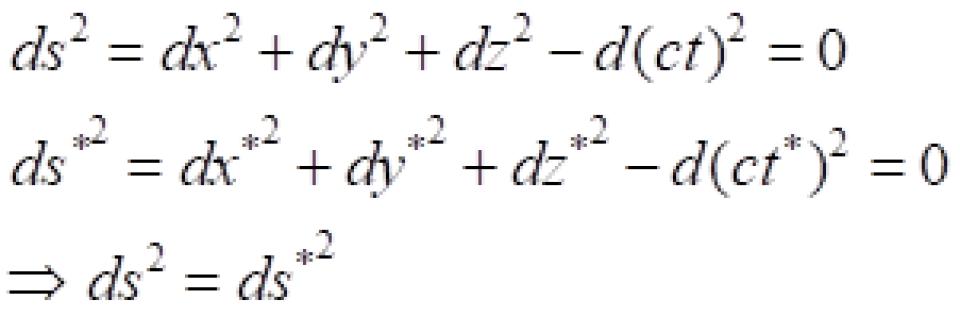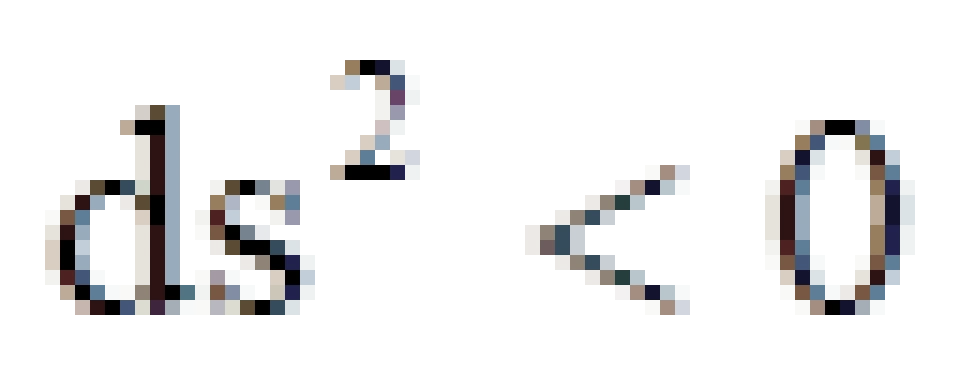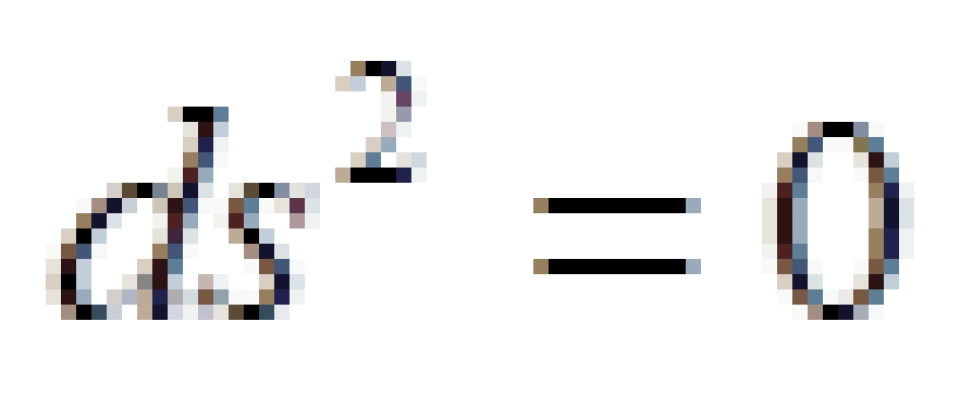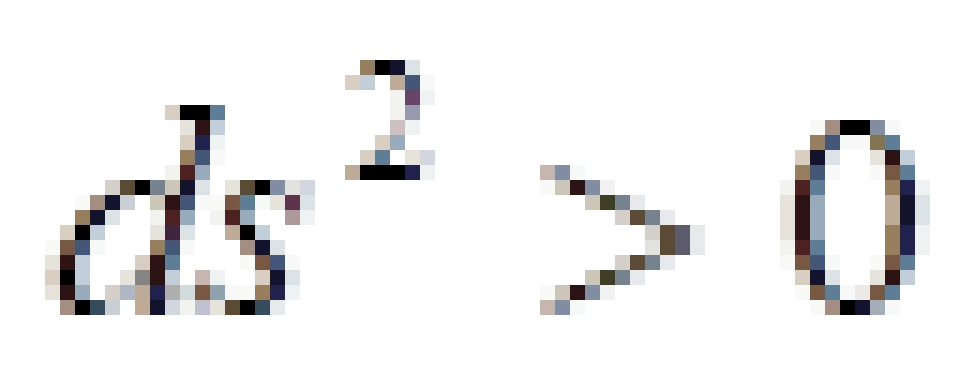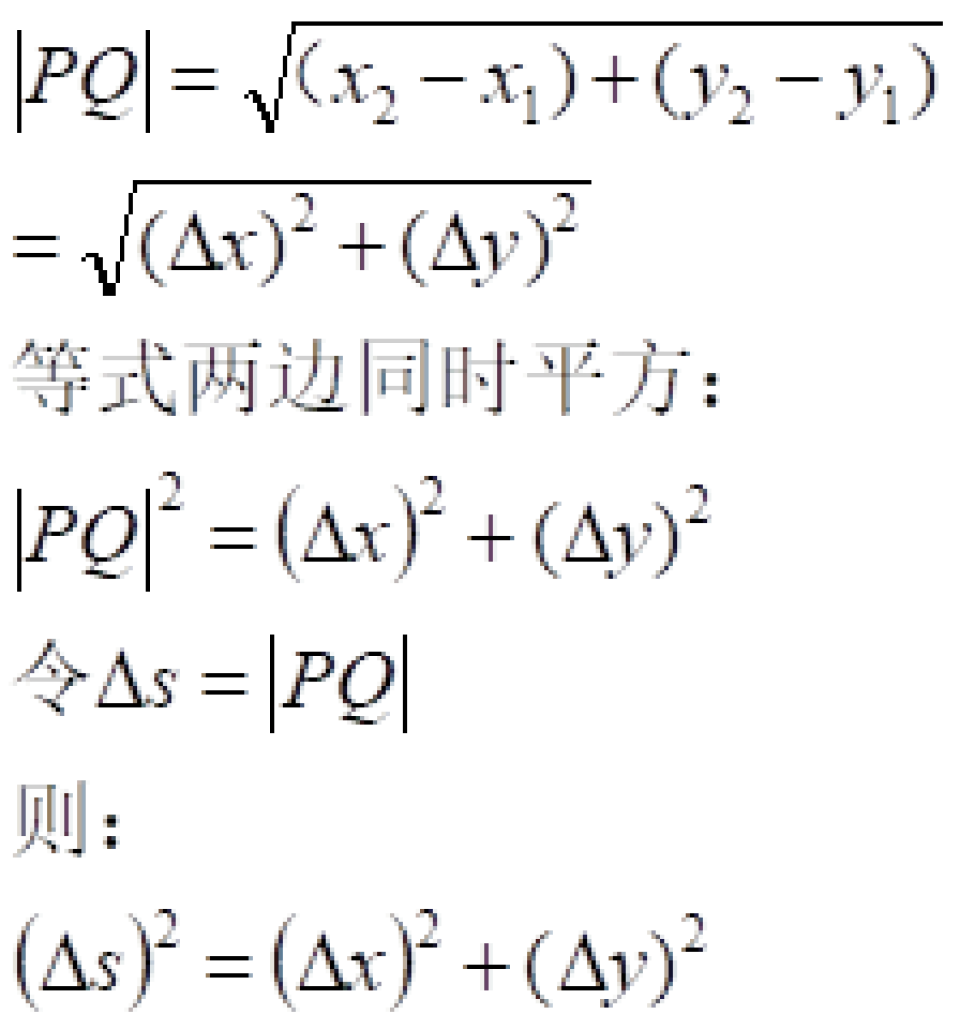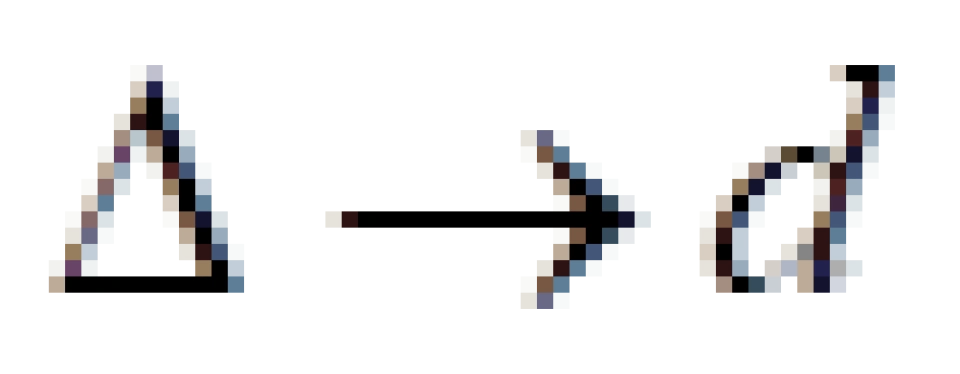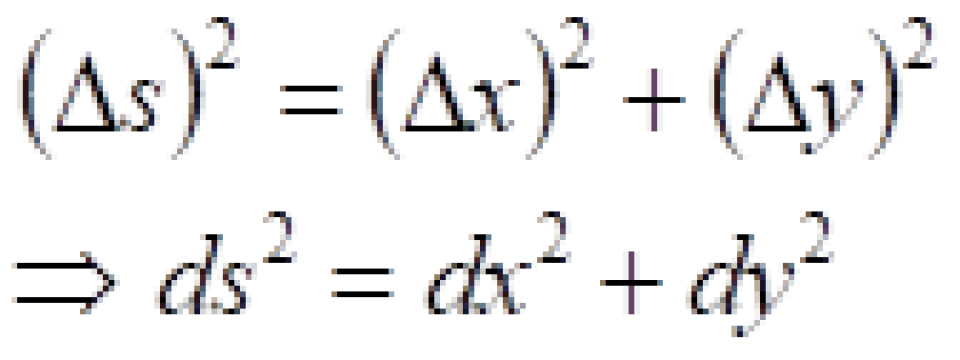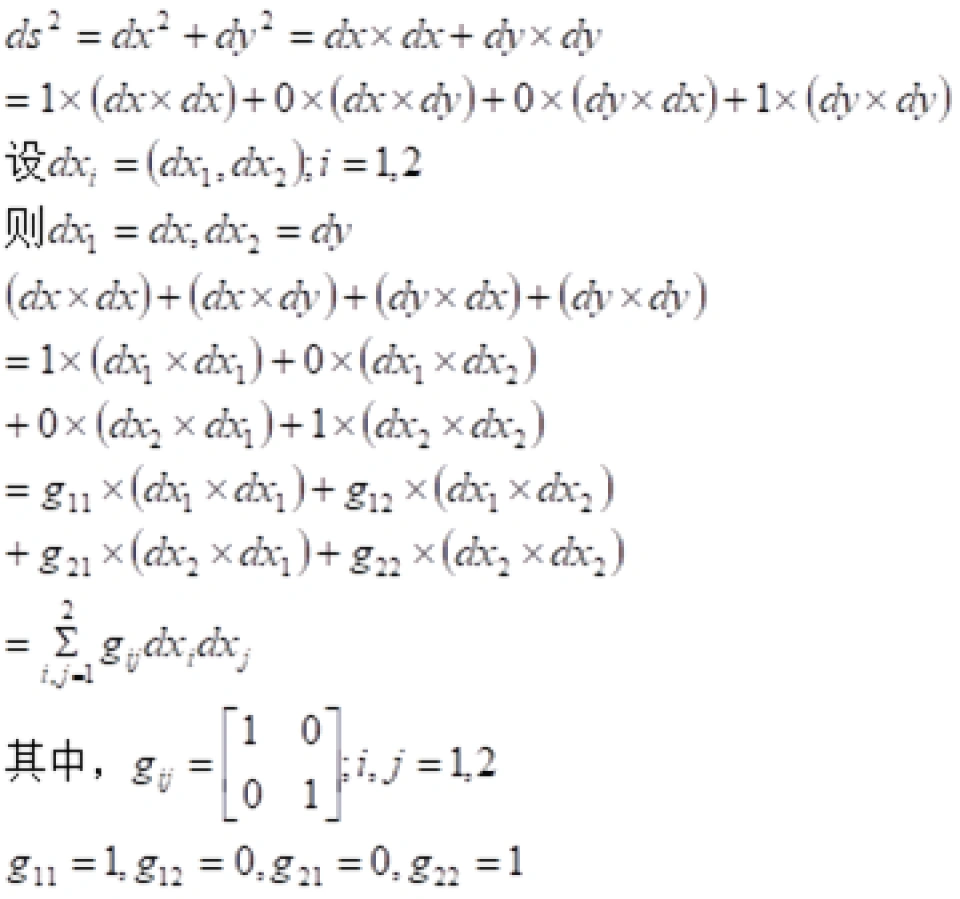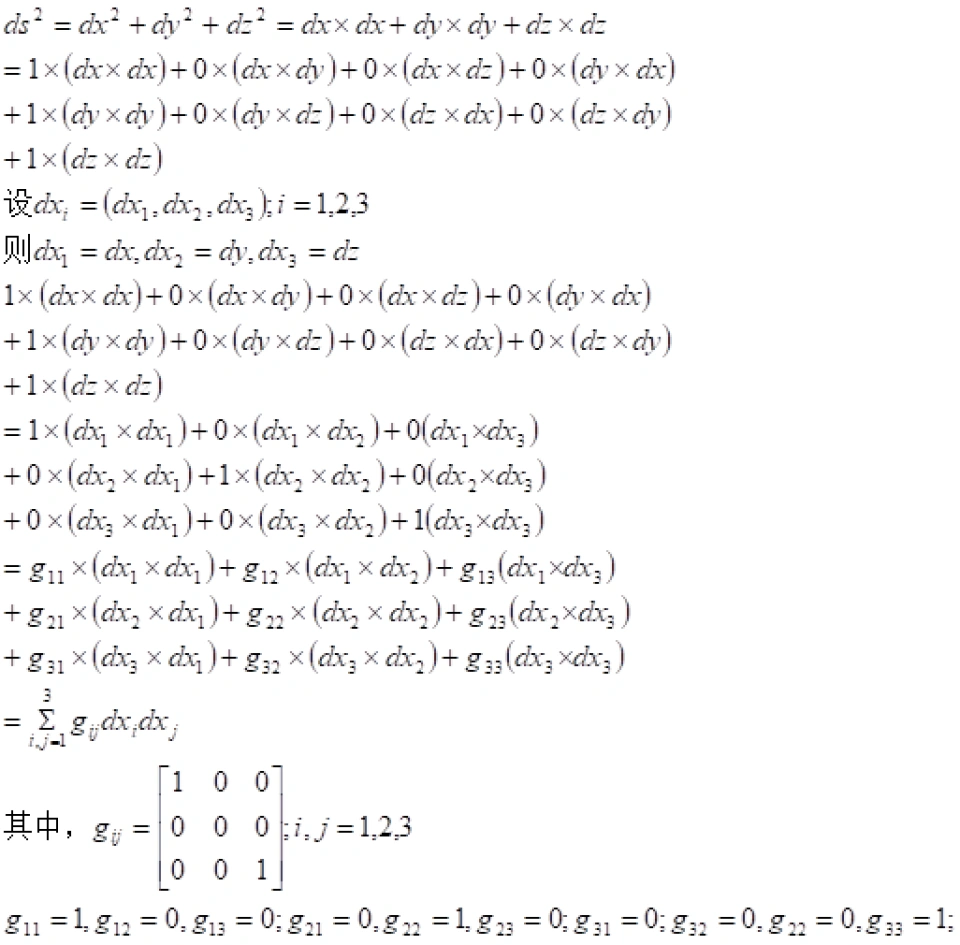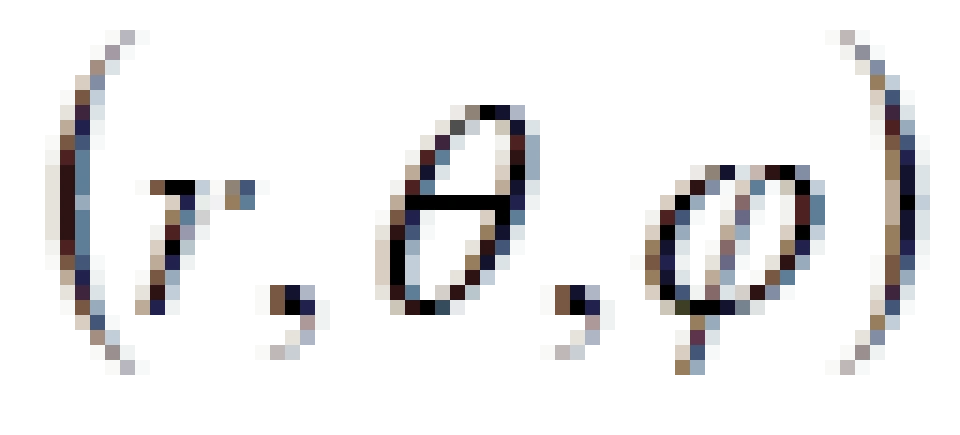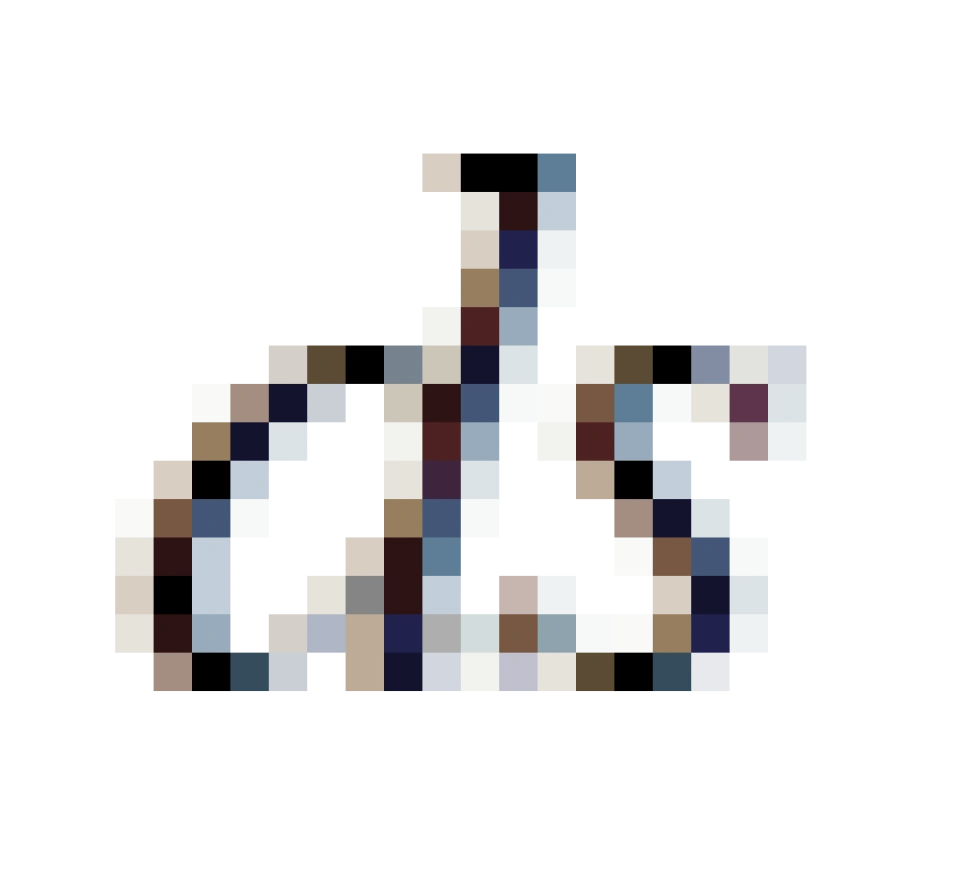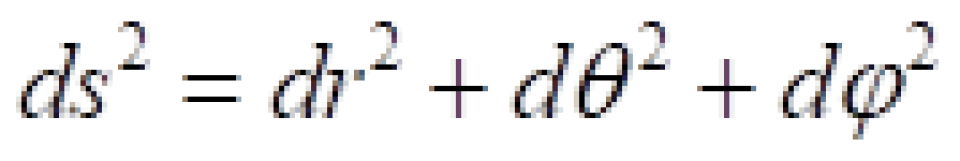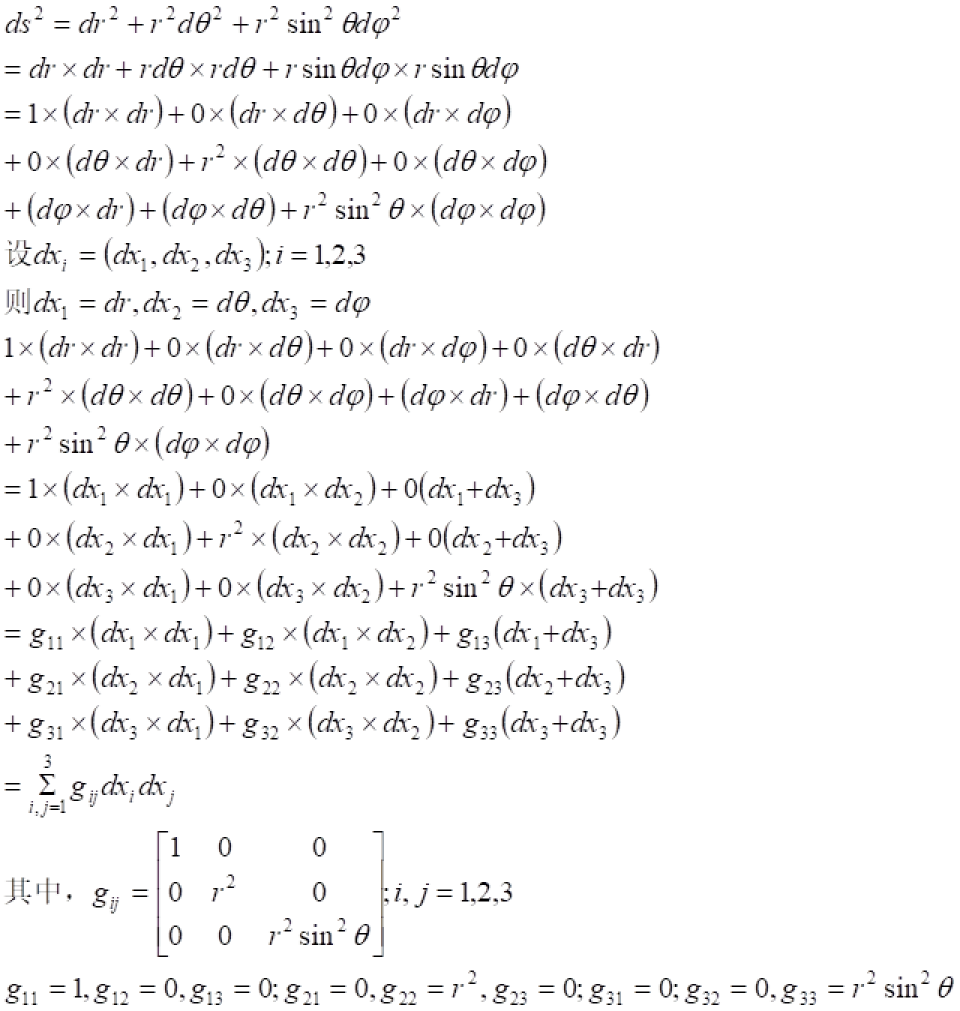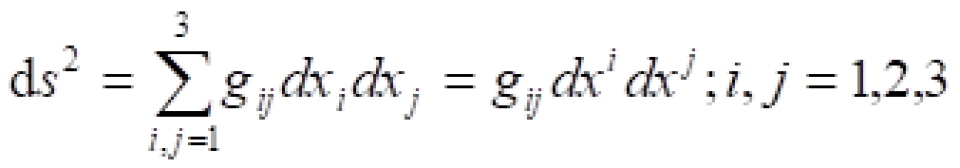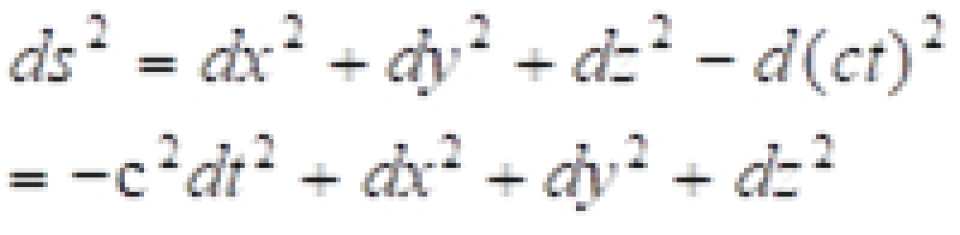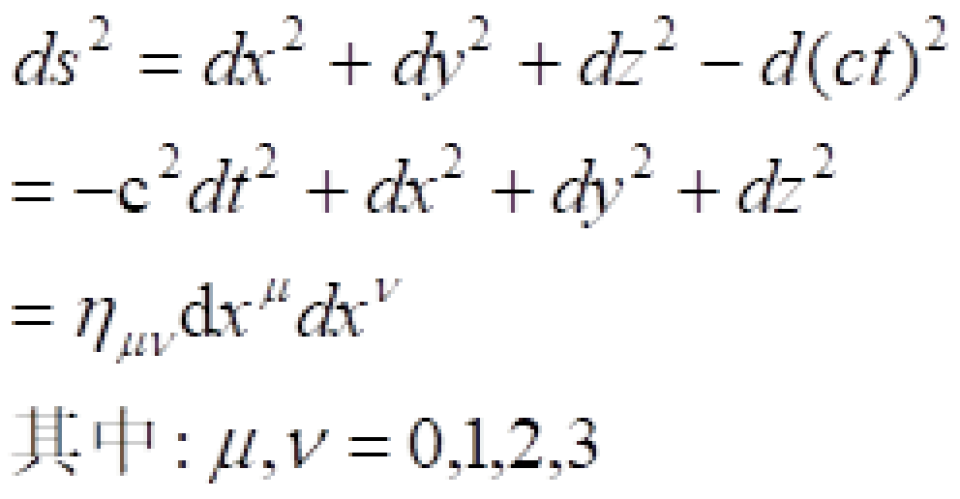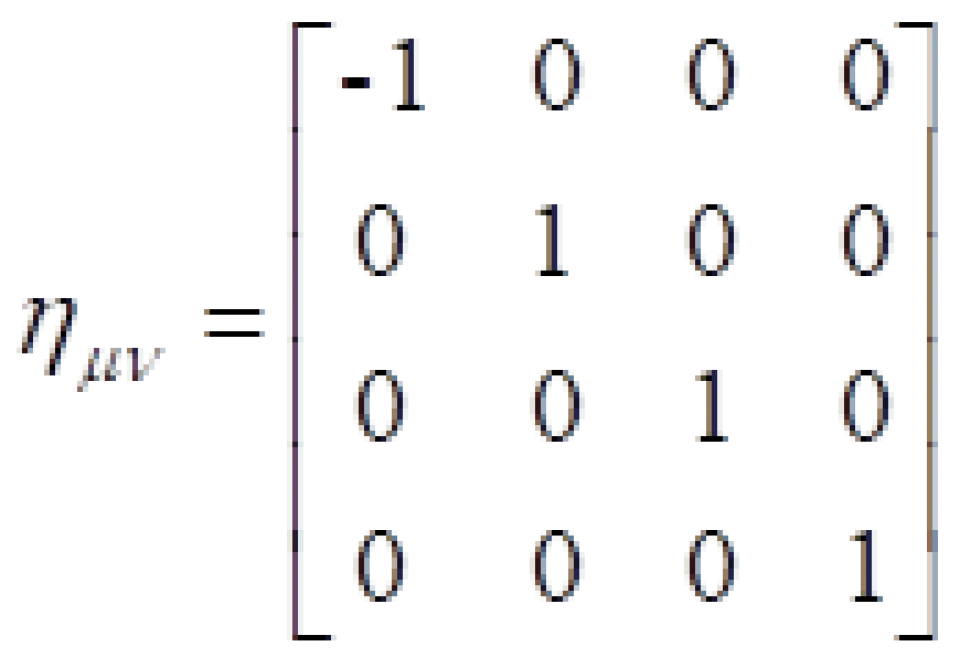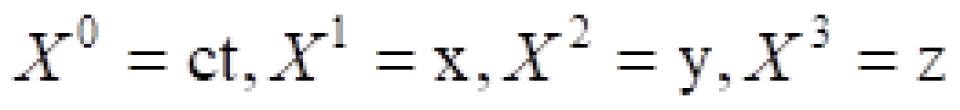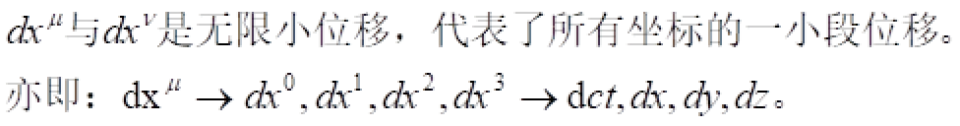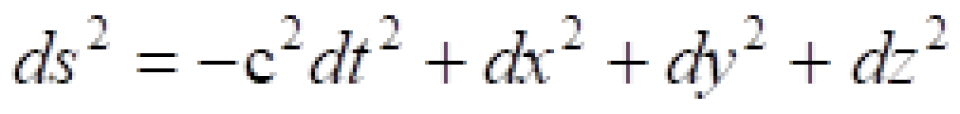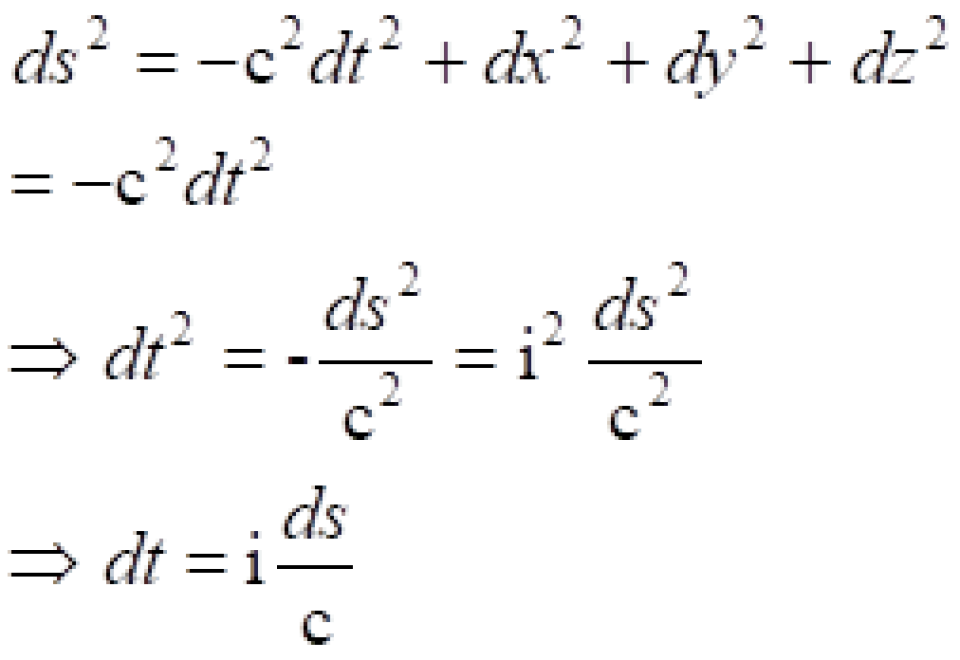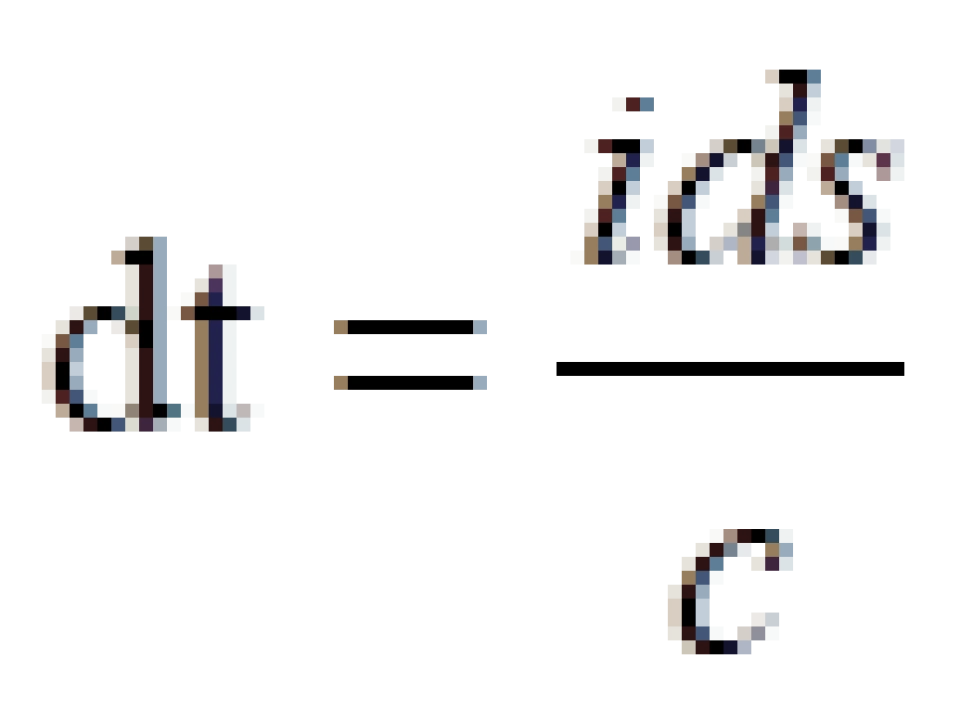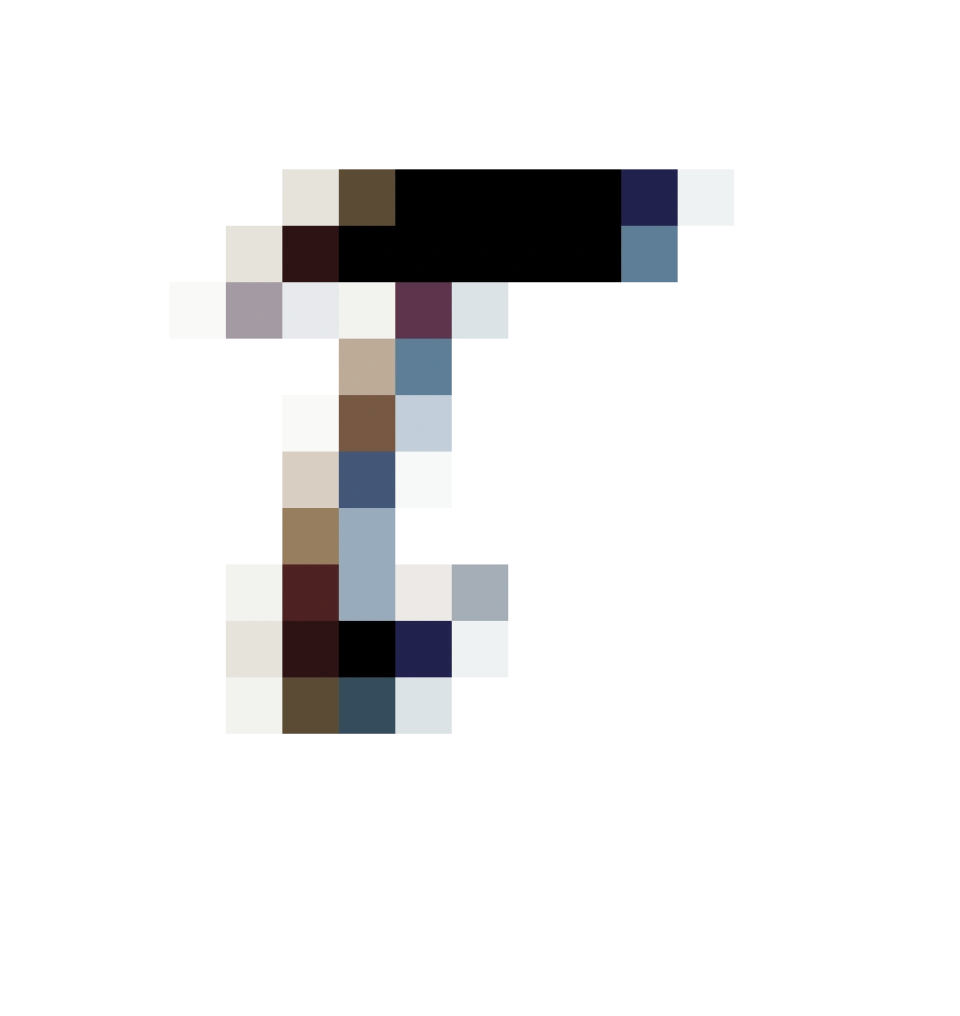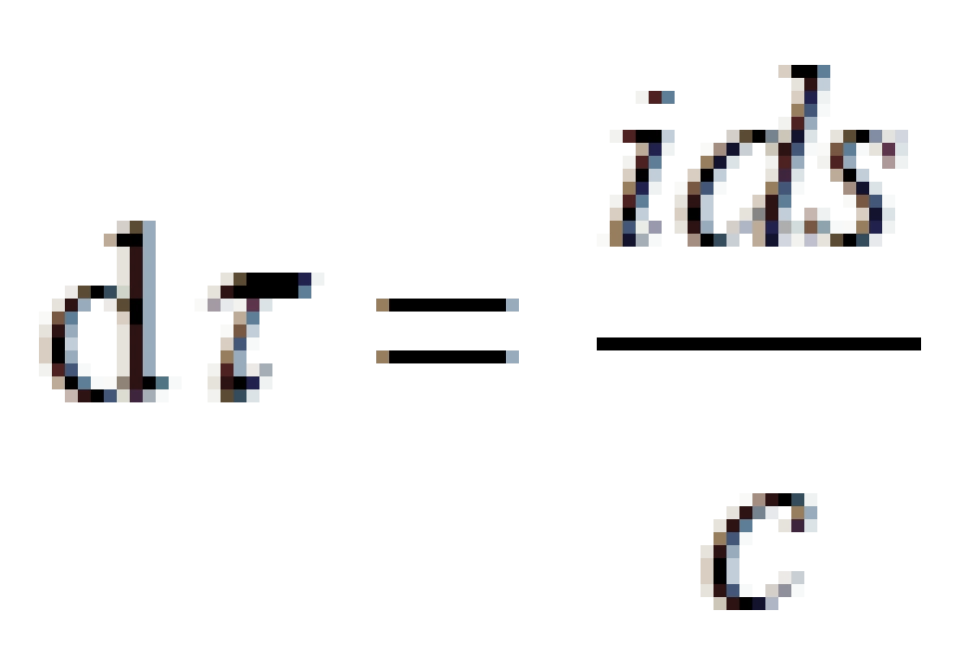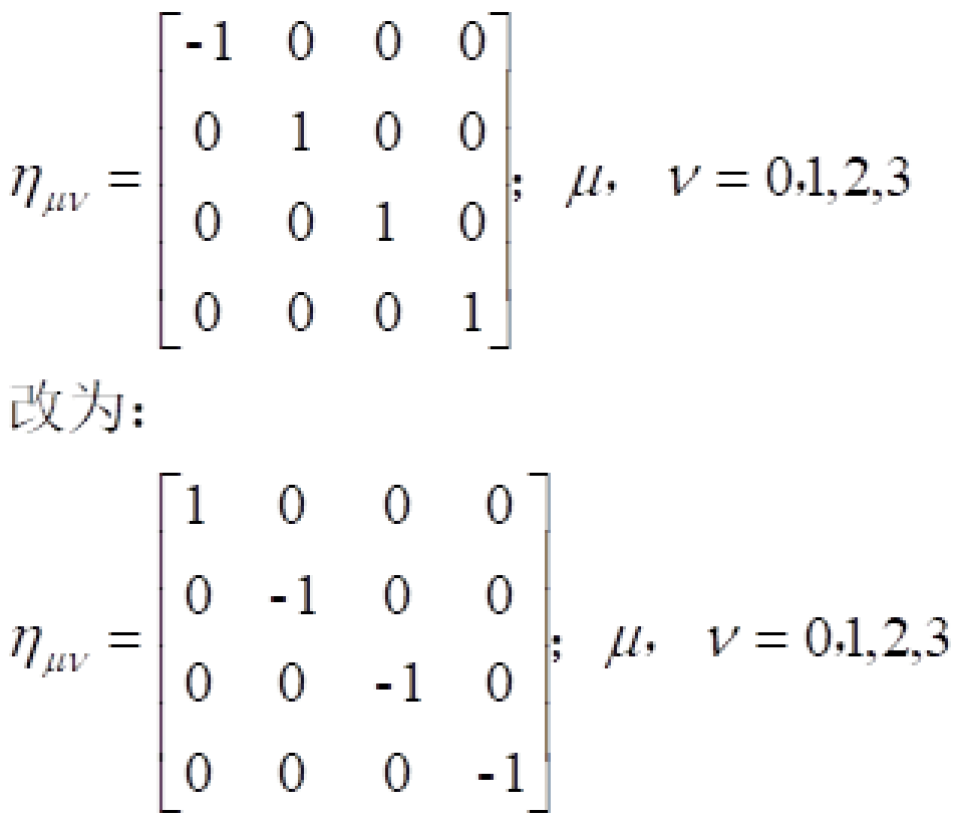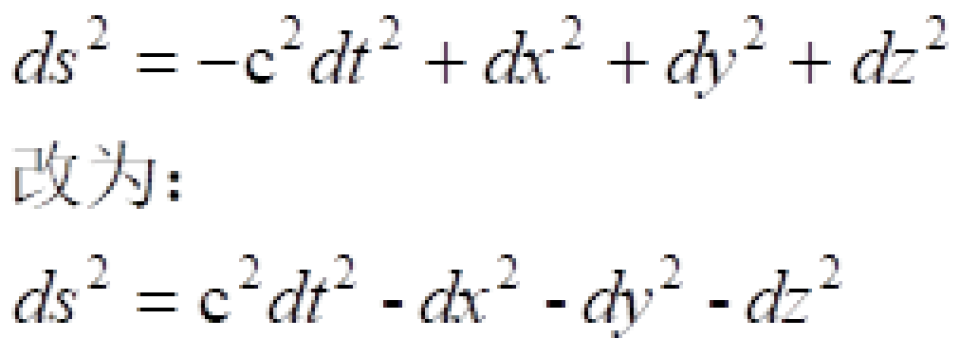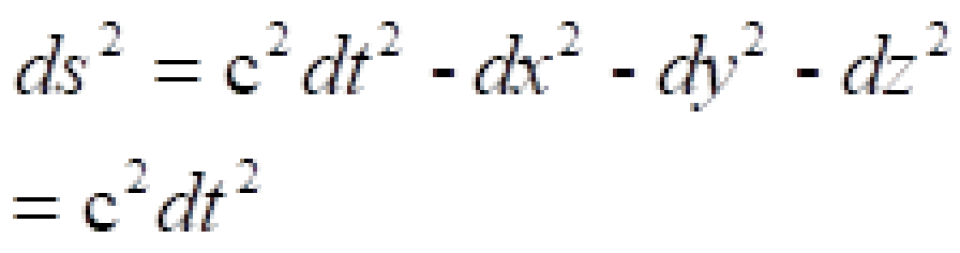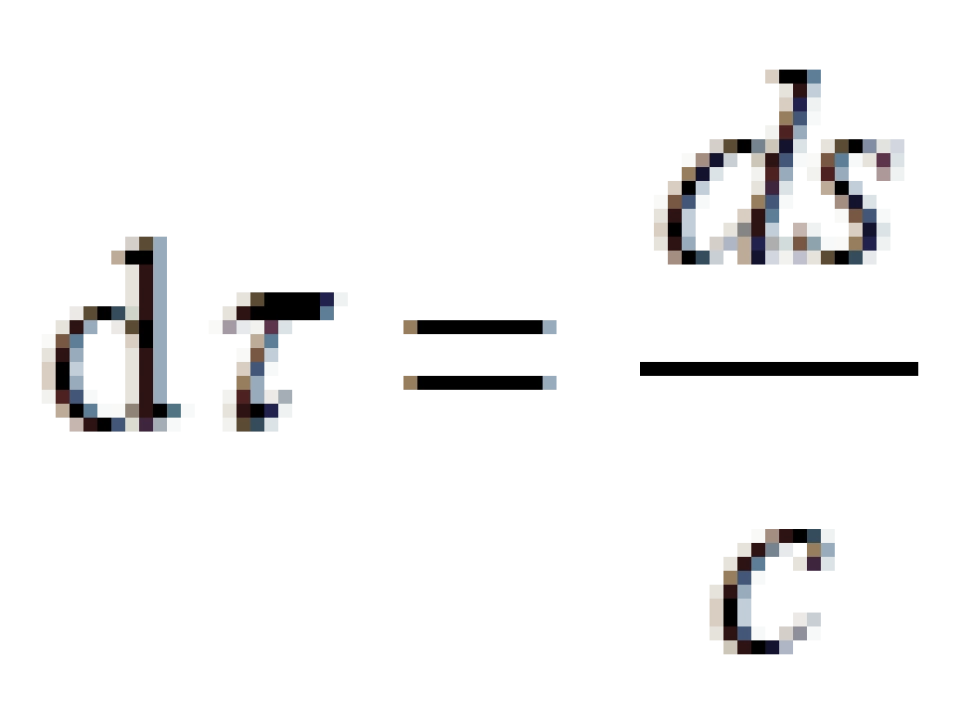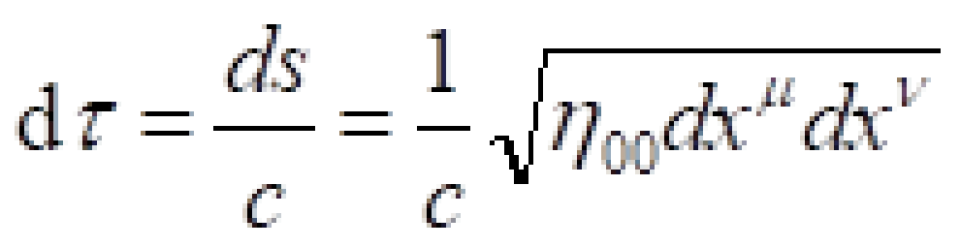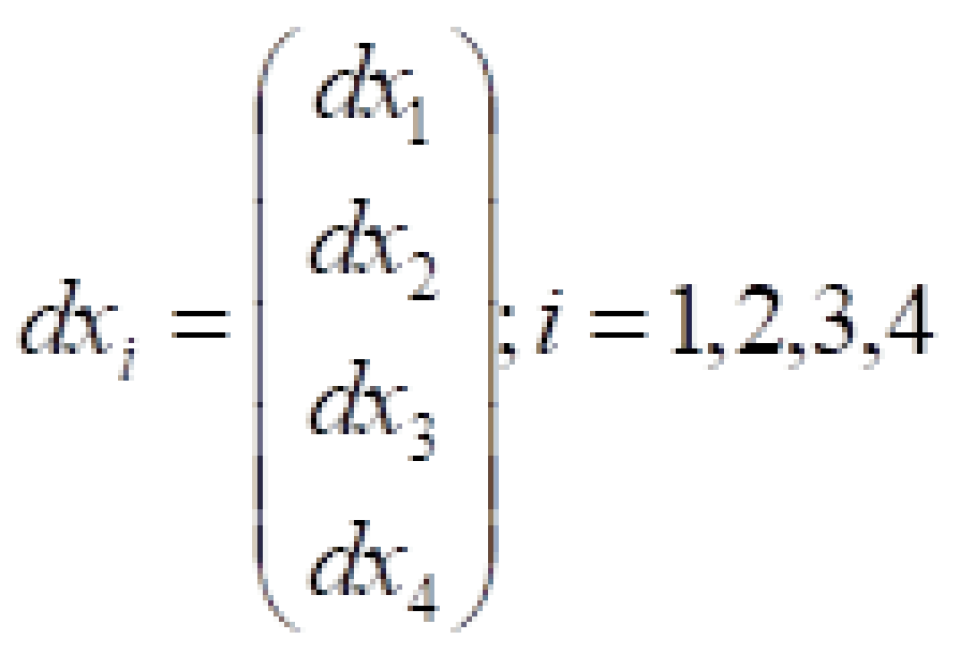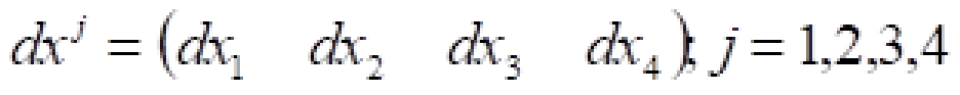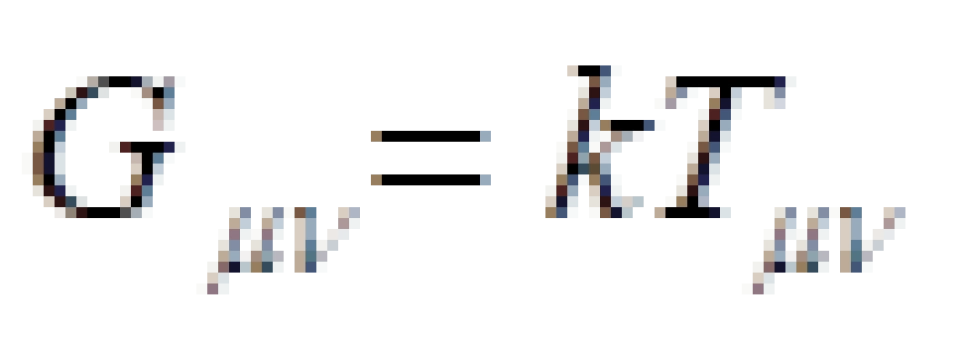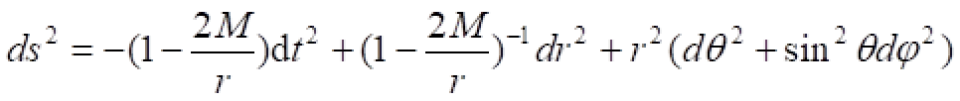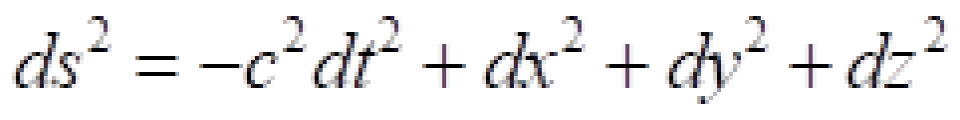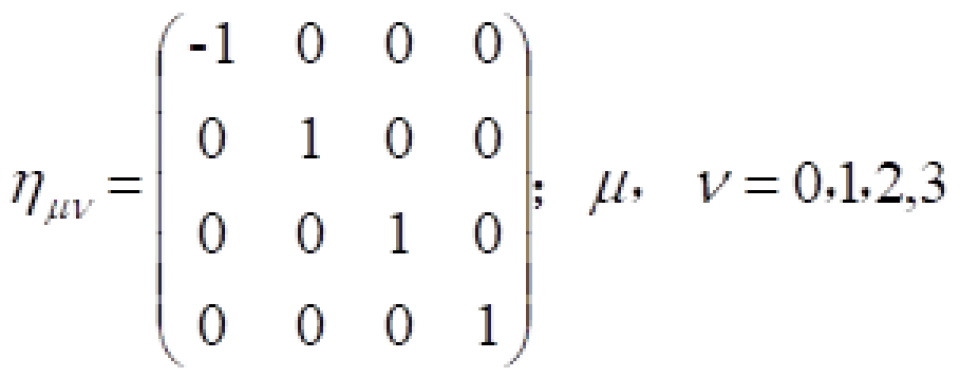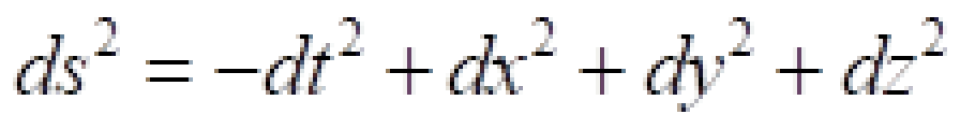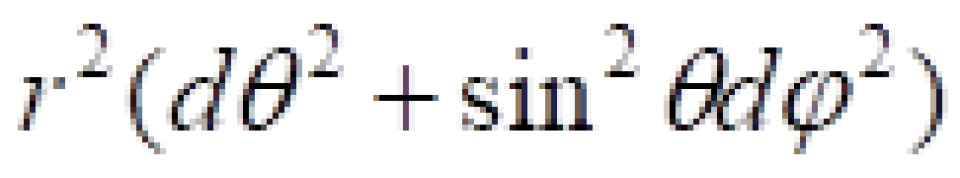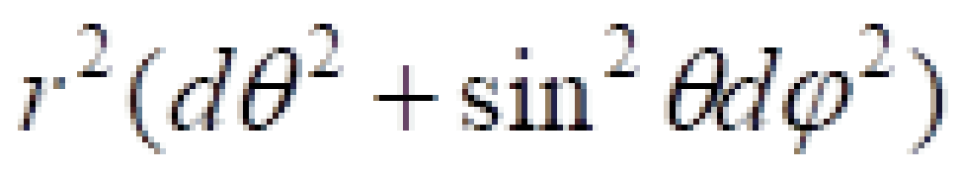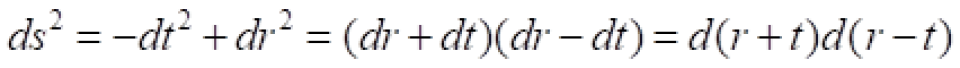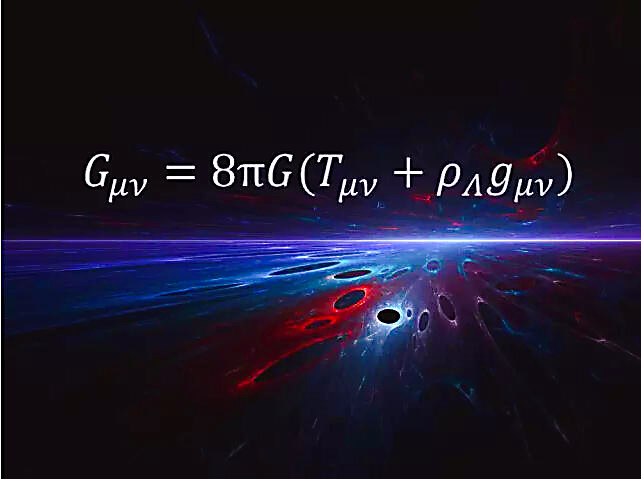科普驿站 第二期
科目：物理/天文
难度：B2-C1
讲师：弦轴子
（注：手机上查看可能部分公式图片无法完整显示，可以点开相应图片查看完整大图）
英国自然哲学家艾萨克.牛顿提出万有引力定律，可是当时万有引力定律并不可以直接用来实际计算，原因在于万有引力常量G是不确定的，人们当时不知道它等于多少。一直到18世纪，英国人卡文迪许测量出来数值时，人们才可以真正使用它。因此，在整个18世纪自然哲学家们相信绝力现象是绝对服从于万有引力定律的。而且人们也知道光速是有限的。这个可以最早追溯到伽利略，他认为光速不是奔至无穷大的，有限制。据业界传闻，他曾经和他的助手用蜡烛光来测量光速，他们的思想方案大致是这样的：伽利略跟他的助手分别到达了两个山顶，然后伽利略打开手持的灯，并开始计时，等助手看到光时也打开手持的灯，伽利略一旦看到助手的光就停止计时。把这个时间去除两个山顶之间距离的2倍就得出了光速。
但是这种方法的误差是很大的，尤其是我们知道光速现在是30万公里每秒。所以这是他们的第一次尝试，不可能测到有效数据。不过最重要一点是，人们意识到了光速是一个有限的速度。
来自丹麦的天文学家罗默就想到了一个绝对好巧妙的方法去测量光速。他发现木星的卫星木卫一在木星上的投影做周期性变化，觉得光速可能是有限的。通过望远镜对木星的卫星在围绕木星轨道所发出的光的测量值到了光速具体是多少。
具体的方法是这样的:罗默发现，地球最接近木星时，木卫一的公转周期是42.5小时，而地球远离木星时，木卫一从阴影中出现的时间会比预测的时间越来越晚，这说明随着地球和木星的距离越来越远，光需要更多的时间传递信号，就是说光要通过行星之间增加的距离，使得计时的信号在第一次和下一次之间因而延长了额外的时间。当地球向木星接近时，情形则正好相反。
他得出的值大约是20多万公里每小时。虽然这个数字跟现在的测量误差很大，但在当年也是一个很好的结果了。
在1783年的时候，英国的自然哲学家约翰.米歇尔便利用牛顿万有引力定律与光速有限大胆的假设，存在这样的一颗星球，它的引力大到光都无法逃脱。这乍一看跟我们现在对于黑洞的定义差不多。其实他的当时的认识程度仅限于他认为光仅仅是个微粒。他认为在一颗星球的表面，以某个初始速度抛出一个微粒，让它自由向上运动，但是如果初始速度太低，星体的引力会减慢微粒的运动速度，从而将他拉回来。但是如果初始速度足够大，那么引力将无法把他拉回来这样，这颗微粒就会逃脱。这样就可以找到逃逸的最小初始速度。约翰米歇尔可以运用万有引力定律计算出逃逸速度。他认为存在一个星球，它的逃逸速度是光速。当时的物理学定律是无法阻止这样天体的存在的。因此，他认为自然界是存在这种黑暗的星体，尽管我们看不到它。
13年后，法国的自然哲学家拉普拉斯也做出了相同的预言，并写于他所著作的《宇宙体系论》中。可是到1808年的时候，英国的托马斯.杨发现光有干涉现象，从而验证了惠更斯提出的光的波动学说。所以这将预示着光的微粒描述被打入了死牢。但是人们不知道引力是如何作用在波身上的。所以拉普拉斯就把他这一节全部删去。一直到广义相对论提出之前，这里思想再也没出现过。
1915年11月，阿尔伯特爱因斯坦向普鲁士科学院提交了报告，标志着广义相对论的建立。
但是对于广义相对论引力场场方程的解。当时很难找的。原因在于这个方程式十个联立的二阶椭圆型偏微分方程。
不过这难不倒物理学家们。他们可以假设一些对称性的存在一些特殊情况，从而得到一些特殊的解。于是，当时还在德国军队服役，还在前线的物理学家史瓦西在求对称性与静态这两个条件之下，得到了被后世被称为史瓦西的解，得到了史瓦西几何。但是要注意的是这类时空几何适合描述静态与球对称的情况下。
为了能更好的理解这个方程及其解以及你们后面能够听懂我在讲什么；我们简单的介绍一下相对论的数学基础。
闵可夫斯基几何
在经典力学的绝对时空观中时间和空间是绝对的，不受物体的运动和分布的影响。当然在坐标系变换中是一对不变的量。 但是在相对论中却不是。相对论中，时间与空间受到物质的分布和动影运响。
在狭义相对论中时间与空间受到物质的运动影响，即时间与空间在坐标变换中是变化的量。那么存不存在一个量，在坐标系变换中是一个不绝对变量呢？也许可能存在，那我们先来找一下。
我们找了之前要提出一个光速不变原理并认为它作为基础假设中是成立的一个证明。在此之前先讲两个相对论的术语：
事件：就是在某一地点，某一时刻发生的事情。因此也可以被当成一个时空点。
世界线:用于确定物体在时空中位置的线称为世界线。也可以说是物体在时空中的轨迹。
世界线总是依赖于观察者的。两不同观察者对于同一物体可能会画出完全不同的世界线。关于这点想必大家回想起高中飞机上的人和地面上的人观察自由落体会发现轨迹不同，就是这个道理。
现在考虑两个相对运动的惯性参考系，(为了方便计算，我们考虑特殊情况，沿着x或x*方向运动)它们分别是s系与s*系，两者之间的相对速度是V。
P与 Q点是光传播过程中的两个相邻的事件，现在我们研究这两个事件之间光的传播速度。
在s系中，
，
，则有
在s*系中，
，则有
仔细观察上面两个结果，我们不难发现：
因此，我们就找到了一个不随坐标系变换而变化的量。
这只是对于光来讲，是否对于任意两个事件都会有这种可能呢？
这个可以被证明出来可以推广到任意两个事件。
但是，自然界运动并不是匀速直线运动(惯性参考系)，不过我们
只要把时间取得足够短(无穷小)，就可以近似当成惯性参考系来处理。
此时
所以上式就可以改写为:
我们将此定义为任意两个事件之间的间隔元或者是时空线元，记作ds。
对于任意的s系与s*系中，P与 Q点光传播过程中的两个相邻的事件之间的时空线元为：
由上面可知，对于任意的s系与s*系中，P与Q点光传播过程中的两个相邻的事件之间的时空线元相等：
它不随惯性参考系的选择而变化，是我们要找到一个不变量。
这是正因为这种时空间隔不变性，使我们可以把这个不变量当做一个几何量并采用几何的语言去描述物理时空。
ds代表的是两个事件之间时空的间隔，你也可以把它类比成空间中两点的距离或者间隔，只不过这里是在四维时空中两个事件之间的距离。这个量是不随参考系的选择而变化的，也就是不随观察者而变。
由于不变量ds的定义中带有负号，这意味着对于时空中的两个事件,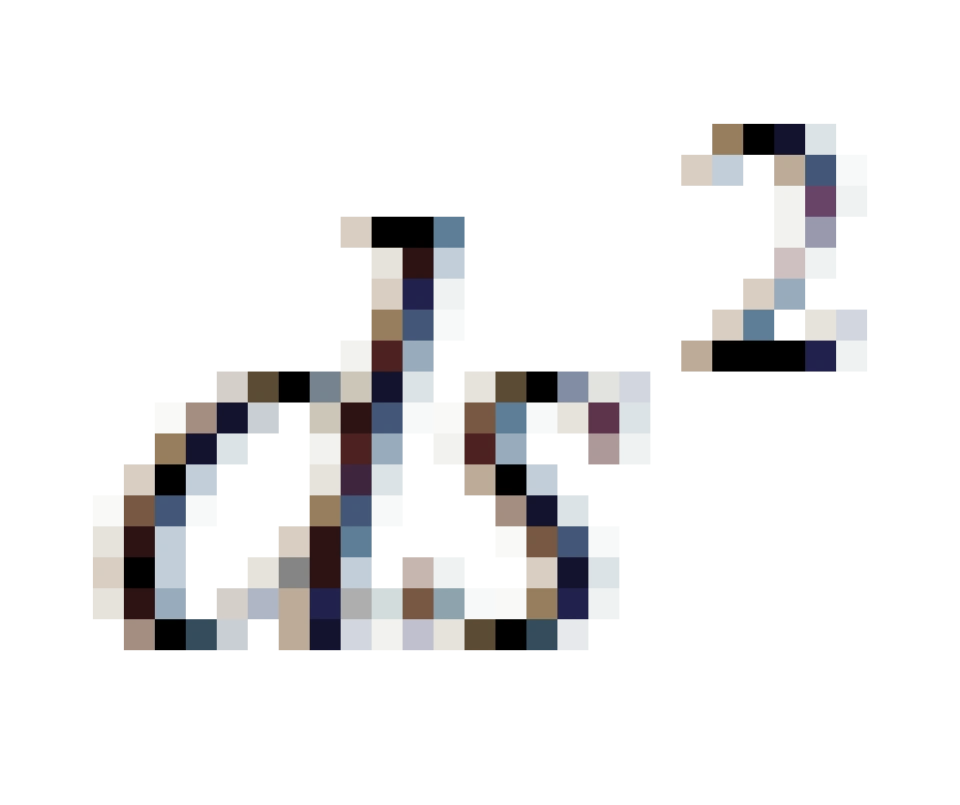
的值可正可负可为零。
因此，我们可以分类：
，我们称之为类时曲线，
，我们称之为类光曲线；
，我们称之为类空曲线。
类时曲线就是有静止质量或者速度低于光速物体运动的世界线。因此，对于任意两个事件之间，你是可以建立因果关系的。
类光曲线就是静止质量为0或者速度等于光速物体运动的世界线。对于任意两件的事件之间，也是可以建立因果关系的。我们就是通过这一特殊的情况来推出惯性参考系变换有一个不变的量。
类空曲线就是高于光速物体运动或者它们的静止质量是虚数单位的世界线。不过，在狭义相对论的框架之中，这个是没有任何意义的，因为两个事件之间无法建立因果联系。
对于我们找到的这个不变的量ds,我们给出的解释是时空中两事件的距离，或者叫做时空间隔，它与我们通常所熟悉的空间间隔不同，他也考虑了时间间隔。
所以闵可夫斯基才说：从现在起，孤立的空间和孤立的时间注定要消失成为影子，只有两者的统一才能保持独立的存在。它完美的将时间和空间统一在一起。让整个时空变成绝对的了。而时间和空间就像矢量分量一样，在不同的坐标系下分量不一样，但是时空的间隔就类似于矢量的模长在变换下不变。
我们将采用去的记法去重新写一遍这个不变量，但是在讲这个之前，首先要介绍一个新的概念—-度规。
度规
度规度量也可以看成是一种测量的标准。好比各个国家有各自的货币，不尽相同。它其实是定义了在一个坐标系中如何度量曲线的长度。
建立坐标系，把每个点的坐标都写下来，用两点之间距离公式来计算距离。
现在我们考虑二维的情况下，我们采用平面直角坐标系。选取任意两点P，Q并且写下他们的坐标：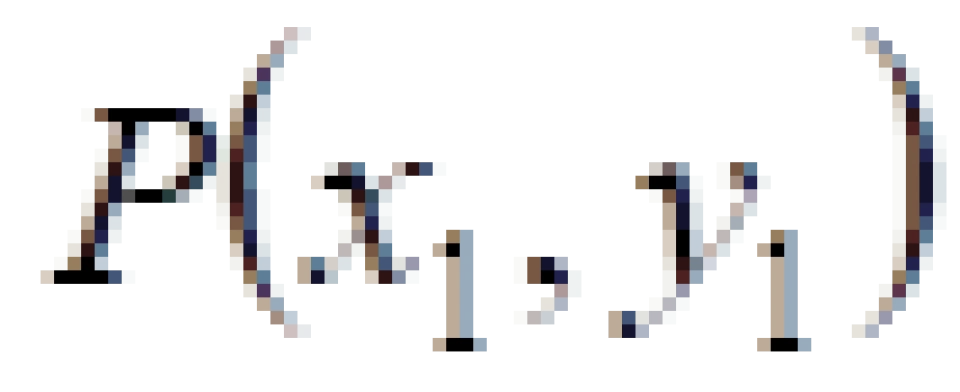
，
。
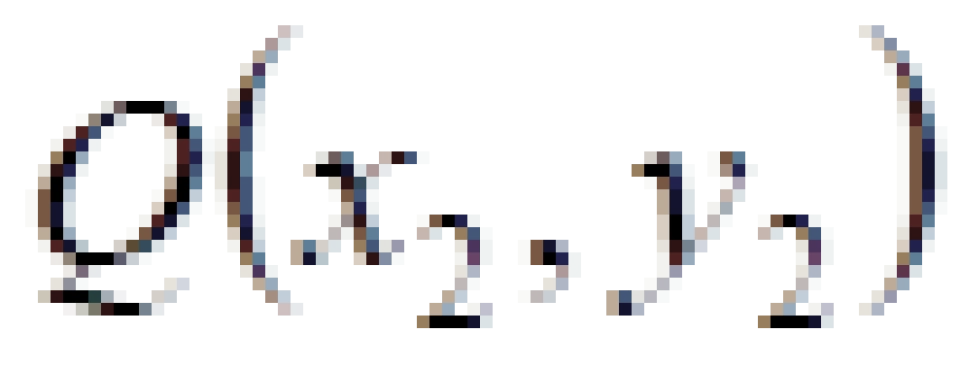那么我们可以很容易利用两点之间距离公式来计算P，Q之间的距离。
这是不是很像勾股定理，其实它就是勾股定理。
如果计算曲线，也可以用勾股定理，只要曲线分成很多段，每一段近似看成是直线，然后用勾股定理把每一段的长度计算出来，再把每一段长度累加起来，只要把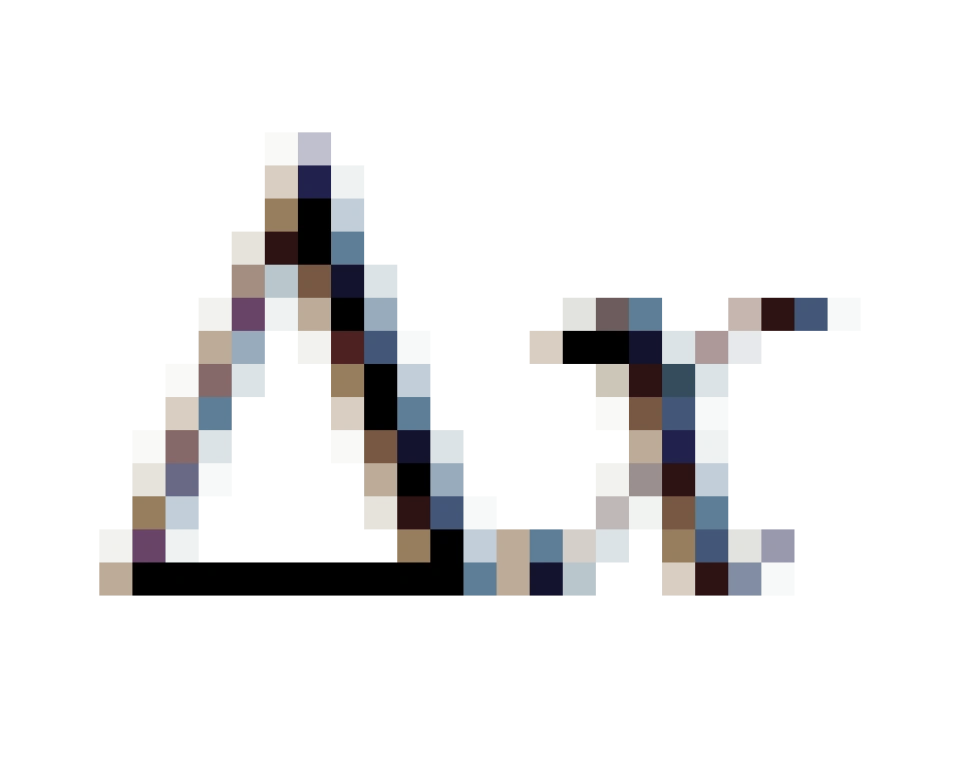 
，
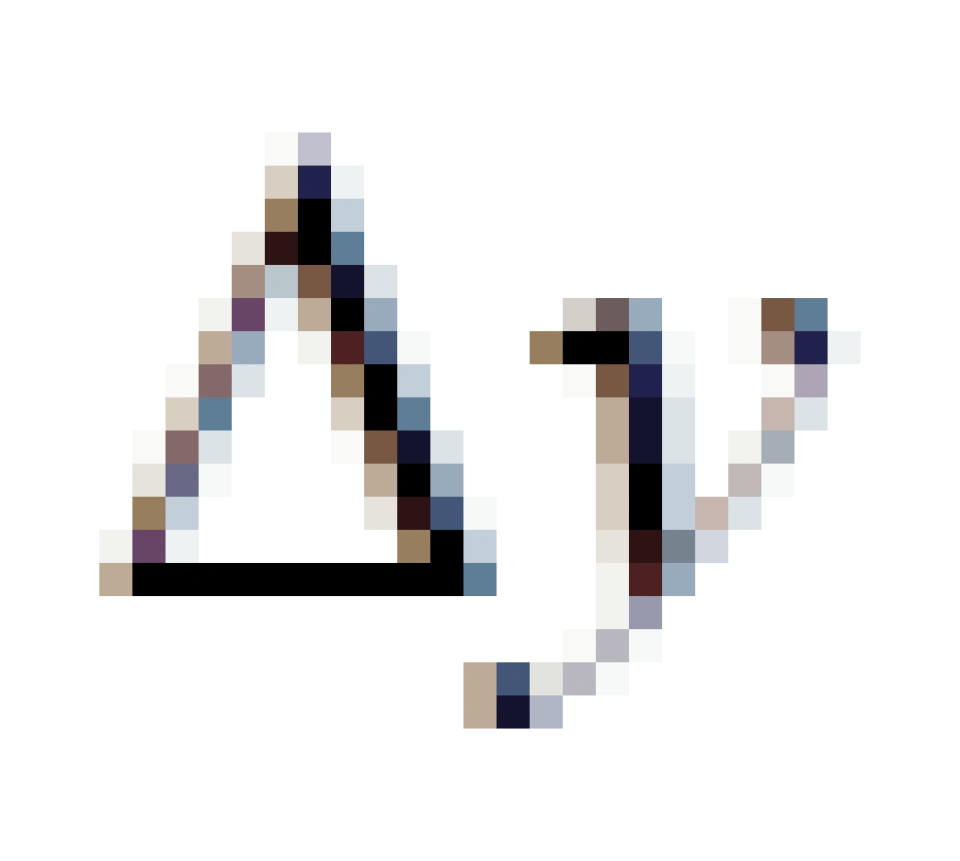取得足够短(无穷小)，就可以当成是曲线的长度。
此时，
。
所以上式就可以改写为:
知道两点坐标，除了用两点之间距离公式来计算P，Q之间的距离，还可以用
上式中的 
是2×2 矩阵，被之为二维欧几里德度规。
按照上面的在二维平直空间中讨论，我们也将结论扩展到三维平直空间中，构造出三维欧几里德度规。
在三维平直空间中,采用直角坐标系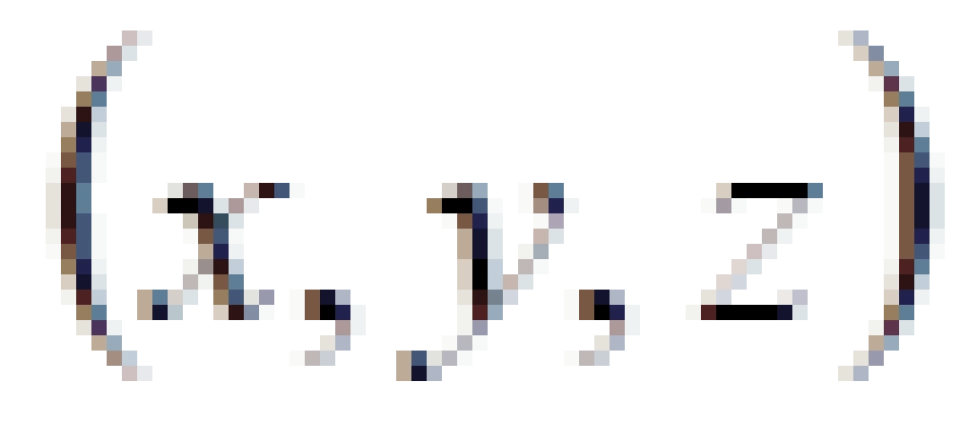 
，任意两点之间的距离 ds可表示为：
上式中的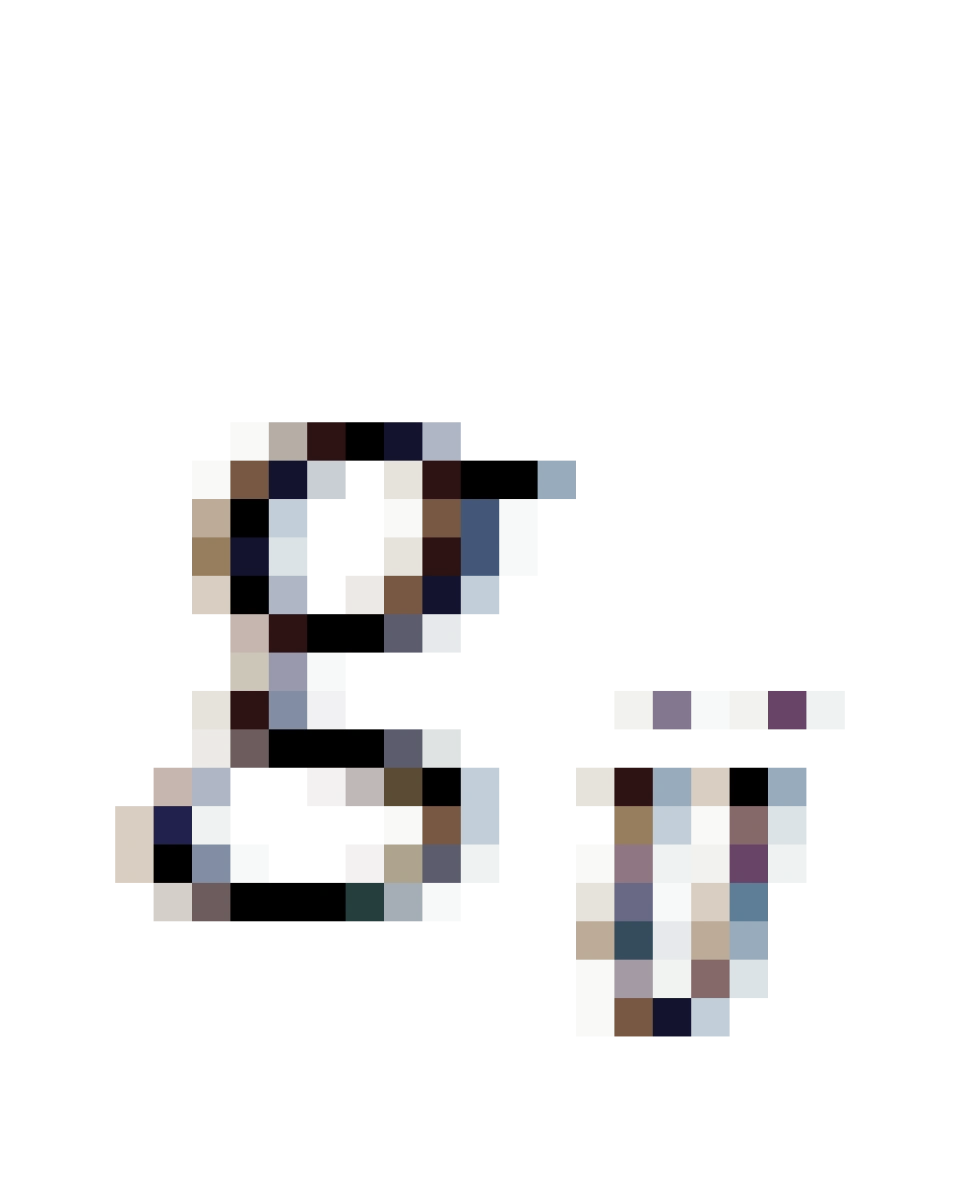
是3×3矩阵，被之为三维欧几里德度规（三维欧几里德度规在笛卡尔坐标系下的形式。）
如果选用球坐标系
, 任意两点之间的距离
则为：
上式中的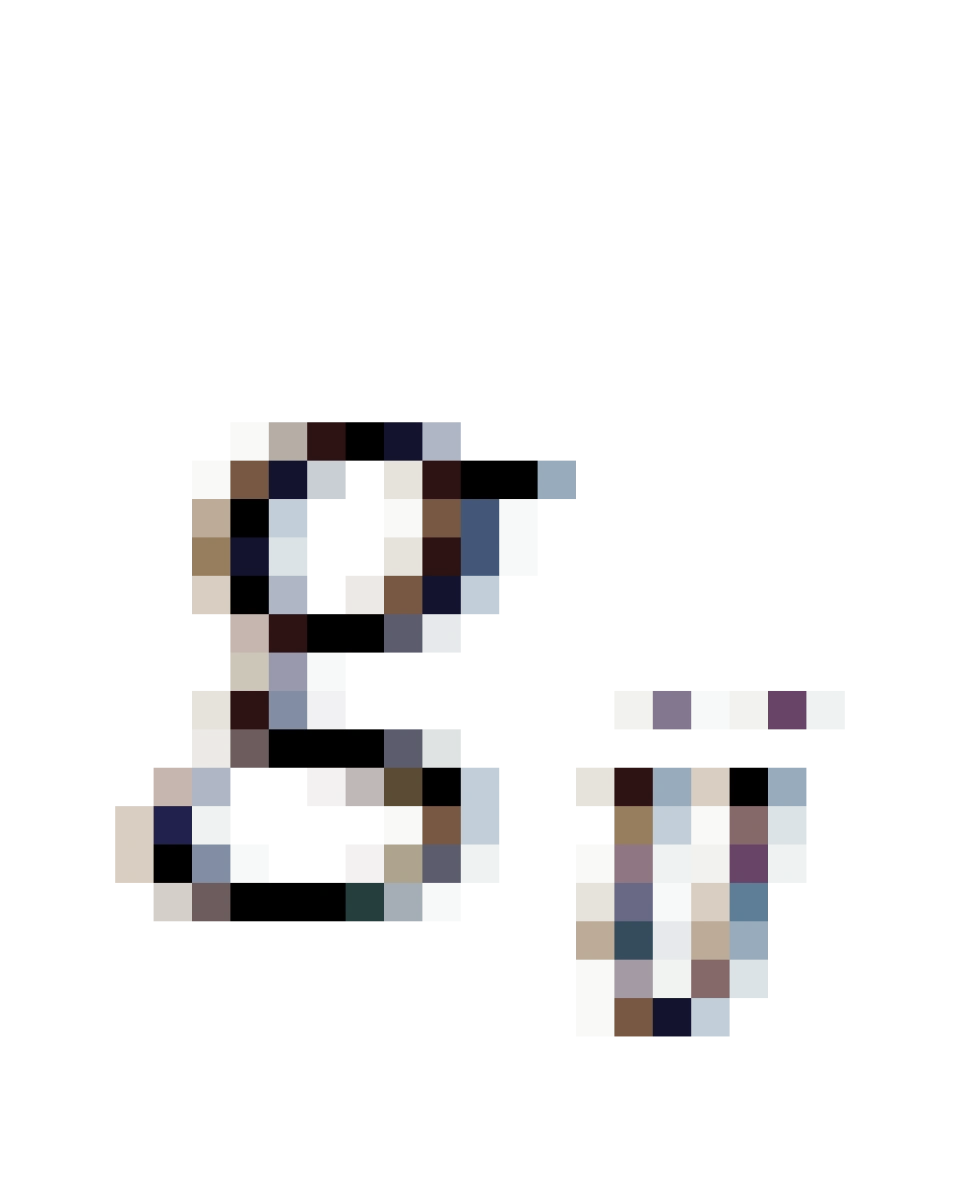是3×3矩阵，是三维欧几里德度规在球坐标系下的形式。
可以看出不管采用何种坐标系，两点之间的距离是不变的。
而我们上面得到那些矩阵就称之为度规，它是在坐标系之中去度量两点之间距离的，通常是矩阵形式。
当然并不是所有度规都归必须只有非交叉项（主对角元素）不为0，其他项(交叉项)皆为0。当然学过线性代数的人一定知道，有些矩阵是可以化为正定形式的亦即主对角元素不为0，其他项皆为0。
度规，可能很难理解，但是举个例子就可以了。
比如，把每个区域类比成每个国家，每个国家使用的法定货币类比成能够完全覆盖这个区域的坐标系。
每个国家都使用自己的法定货币，然后给出这些法定货币的数目关系。
每一处地方都使用自己的坐标系（局部坐标系），然后给出当地计算距离的方法。而决定他们计算距离的方法就取决于度规。
度规就类似于规定的法定货币的数目关系。
可是这些求和符号，写起来太麻烦了，我们可以引入一个求和约定去除这个求和符号。最早由爱因斯坦规定，所以被称之为爱因斯坦求和约定。(这被爱因斯坦私下戏你为自己对数学的最大贡献)
爱因斯坦求和约定
爱因斯坦求和约定：重复指标代表求和，此时求和符号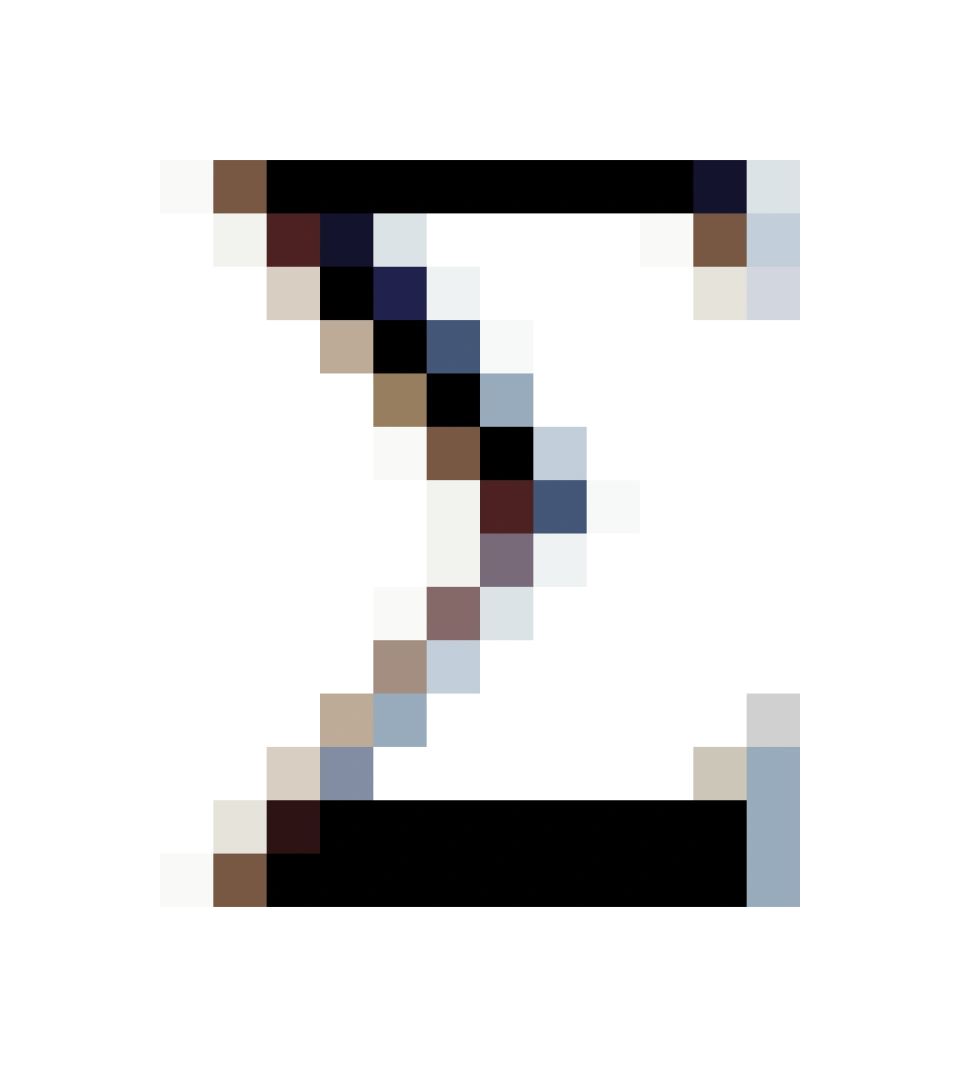
可以省略不写。
条件：1.重复是指求和指标在同一个指标中出现两次（有且仅有）。
2.求和指标在同一个表达式下必须一上一下。
例如：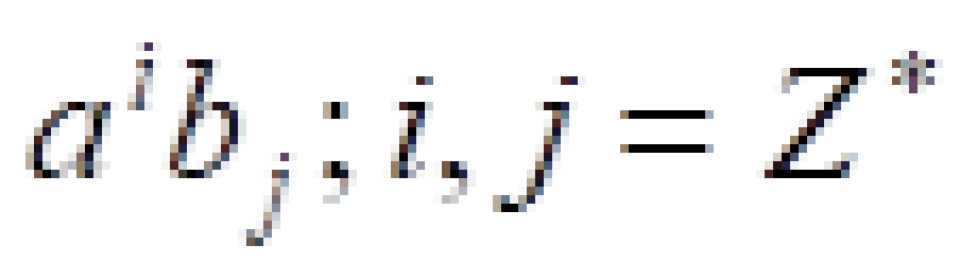
，i,j叫做求和指标，也可以叫做傀儡指标（简称“傀标”），而且可以看出在这个表达式下傀标是一上一下一一对应式分布的。傀标字母没有实际意义，只代表求和；因此，傀标字母是可以任意换取，只要满足上面讲的爱因斯坦求和约定的条件。
现在我们用爱因斯坦求和约定来改写上面度规求和。
条件1：重复是指求和指标在同一个指标中出现两次（有且仅有）。
在上式中,i,j出现两次（有且仅有）,因此，i,j是求和指标也叫做傀标。
条件2求和指标在同一个表达式下必须一上一下。
在上式中,傀标i,j在同一个表达式下是一上一下的。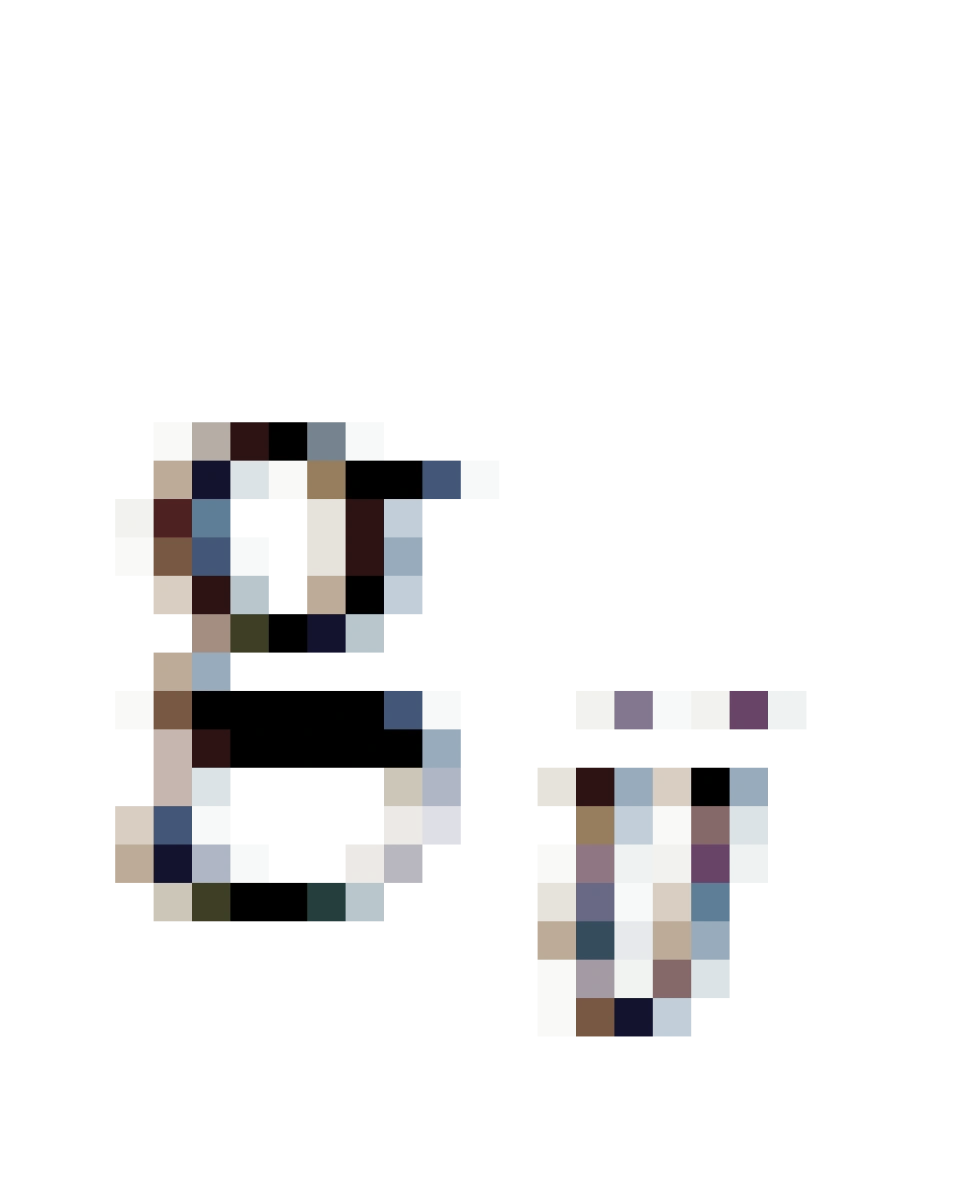 
中的i与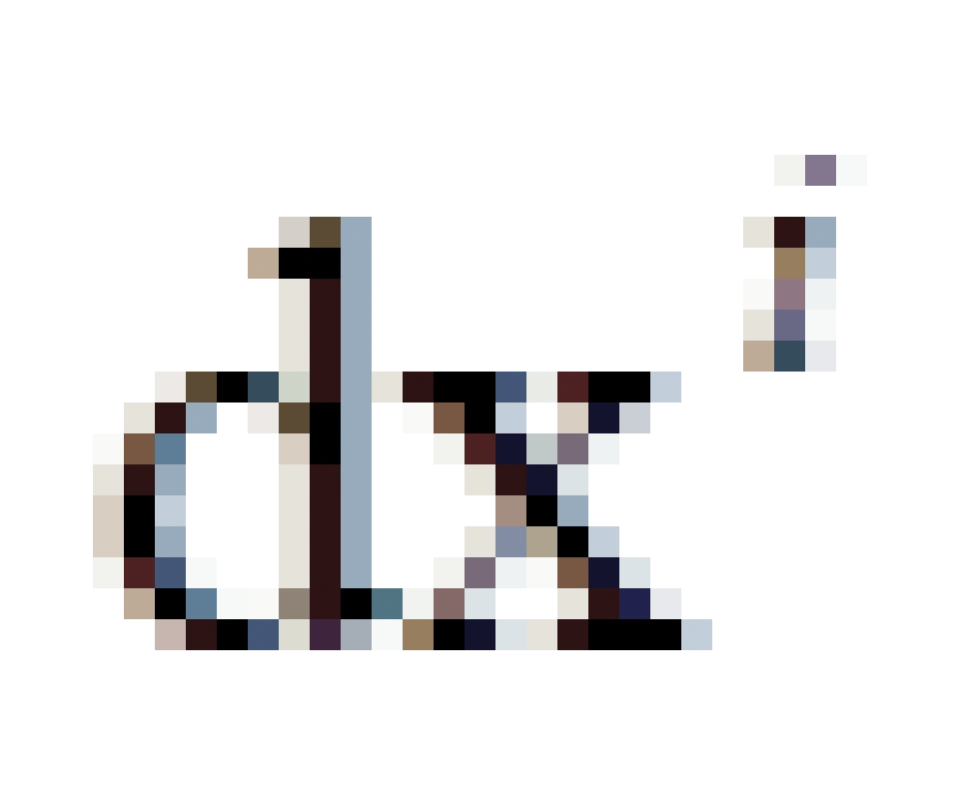
中的i是一上一下，一一对应式分布的, 
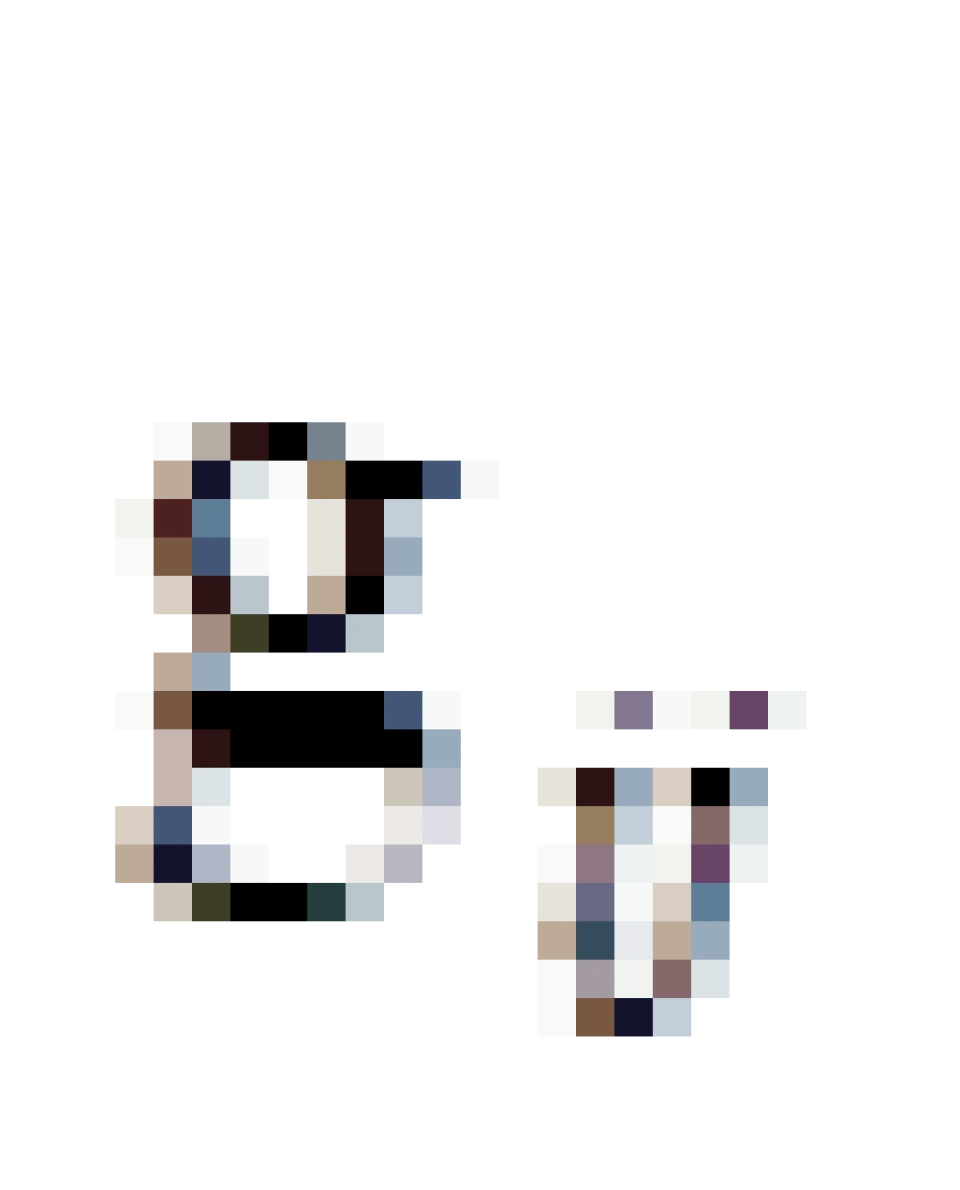中的j与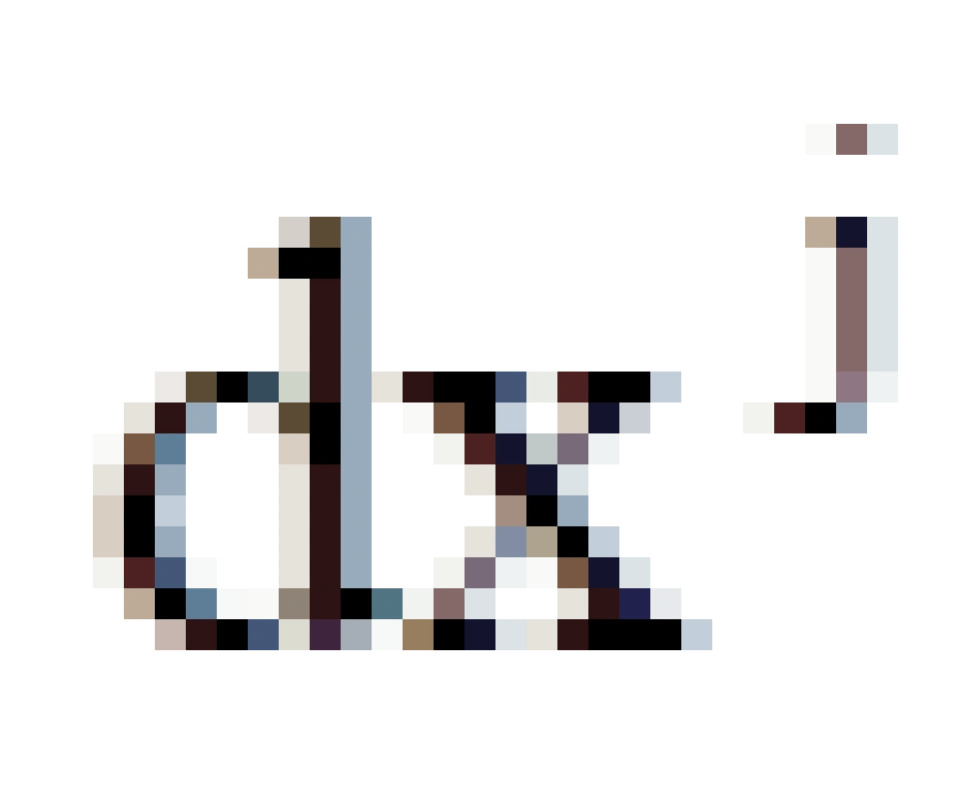 
中的j是一上一下，一一对应式分布的。
介绍完上面这些，我们就可以换一个记法来重新书写我们找到的任意两个惯性系之间的不变量。
这是我们找到的任意两个惯性系之间的不变量。现在我们换一个记法来重新书写一下。
被称之为闵可夫斯基时空度规。在相对论中定义时间和空间四维矢量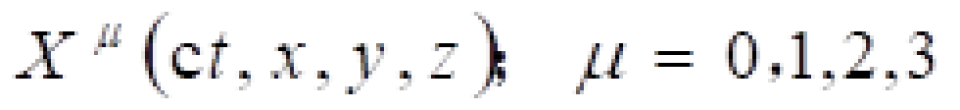
其中
。
固有时间：对对于弯曲时空中的任意坐标系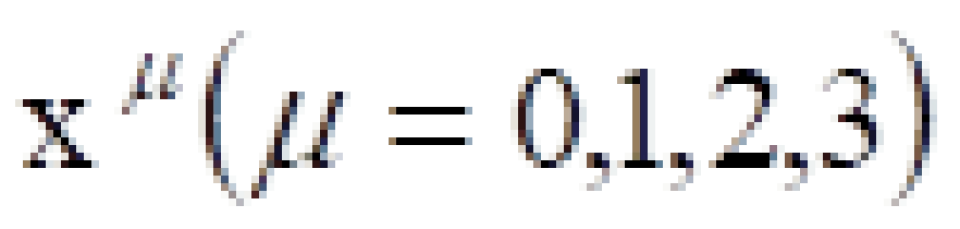
，如果视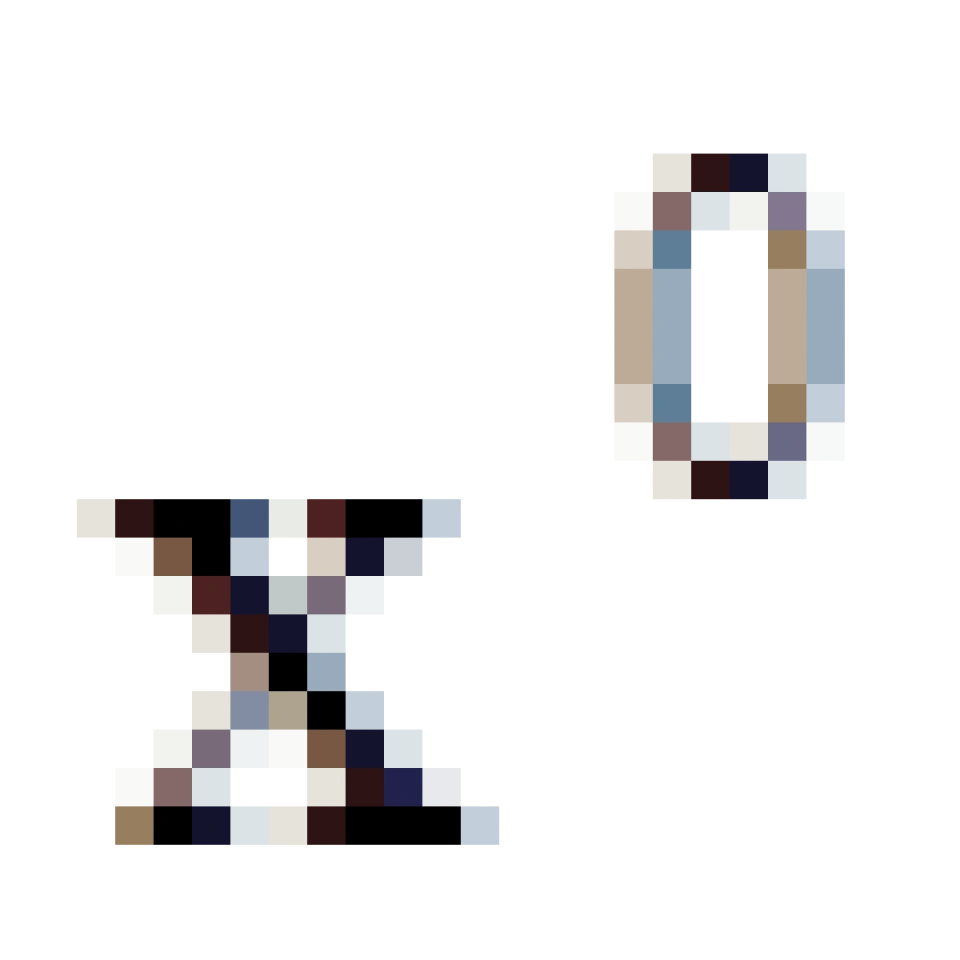 
为时间坐标，则以速率
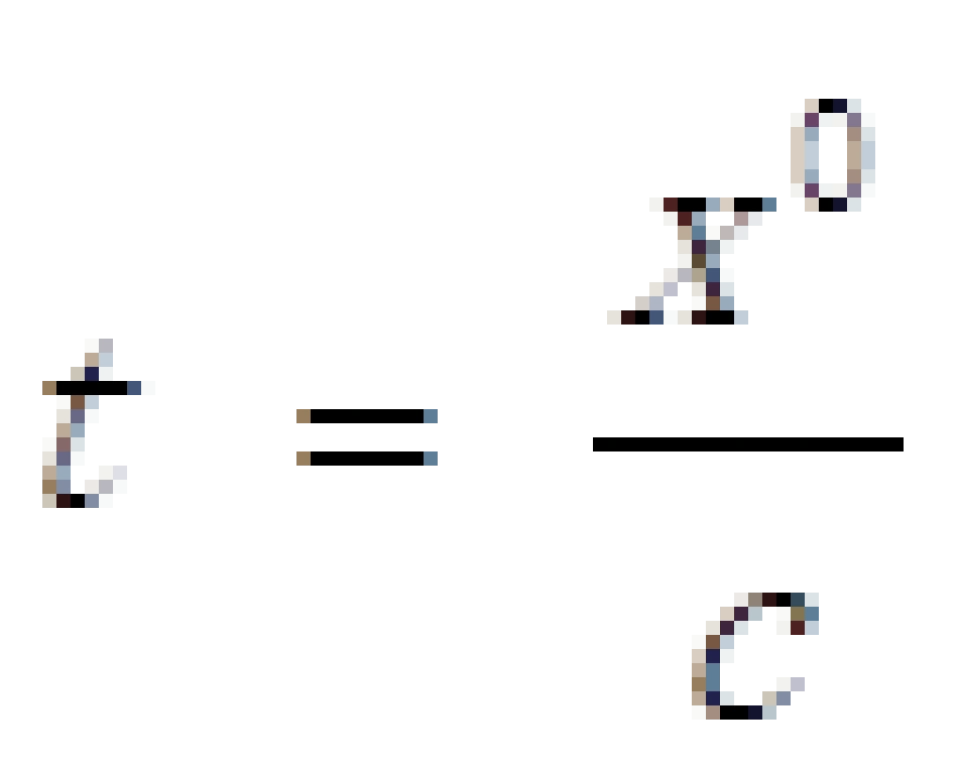运行的钟叫做坐标钟，t称之为坐标时间，c为真空中的光速。
在狭义相对论中，我们称固定于一个惯性参考系中的真实的钟为标准钟，它所记录的时间为那个惯性参考系的固有时间；亦即：静止于那个惯性参考系中的观察者亲身经历的时间。
按照这个定义。再根据我们上面找到的两个惯性参考系之间的不变量：
我们可以知道：
由此可以定义这个惯性参考系的固有时间为：
固有时间用
表示。
不过这有一个虚数单位i很麻烦，但是我们可以改变一下闵可夫斯基时空度规，就可以避免这个虚数单位i。
两个惯性参考系之间的不变量：
我们可以知道：
由此可以定义这个惯性参考系的固有时间为：
不过，聪明的我们也会发现：
这个时候心细的人不难发现，为什么说钟慢尺缩效应是观察者效应。
因为对于两个惯性系之间，时空间隔具有不变性。它们的度规也是。事实上，在广义相对论中会出现更加复杂的度规，他们的对角元也许不是常数，可能是个函数，正是因为这样，才有了曲率。
所以，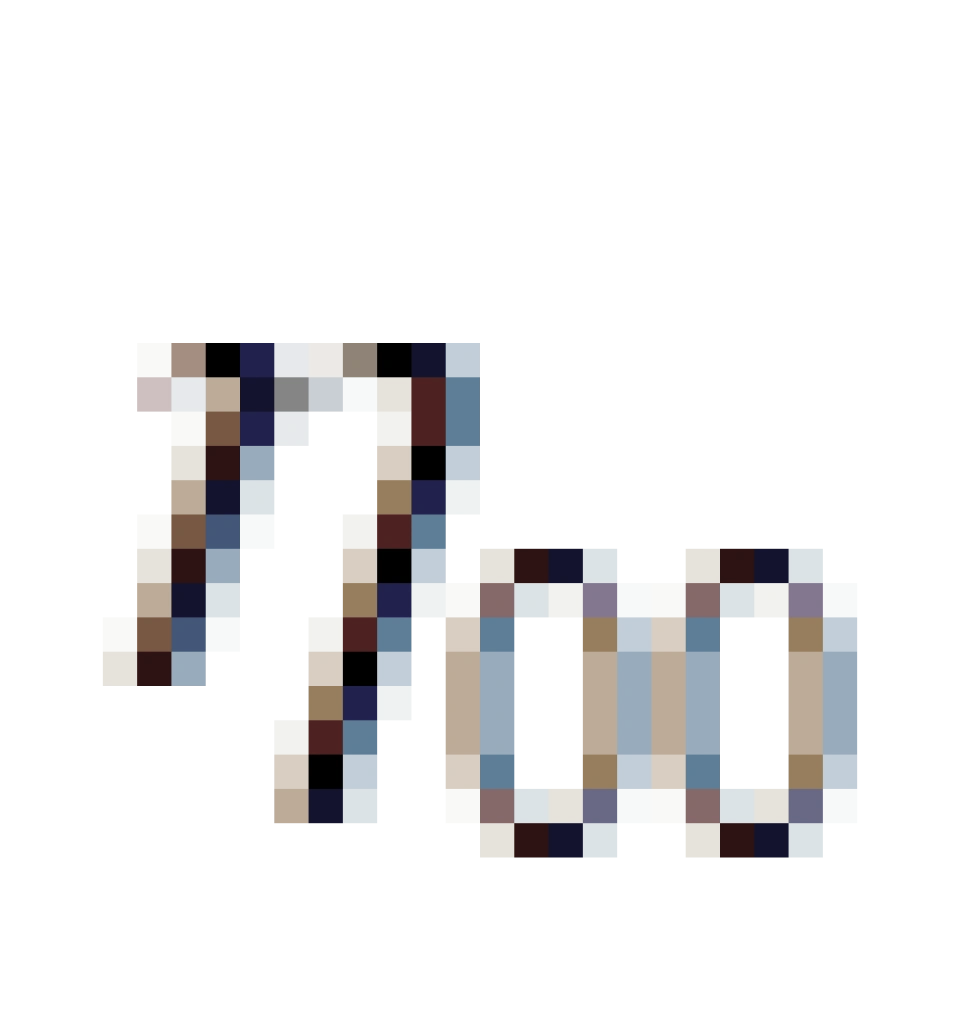 
这个时间项是不会变化的，因此，固有时间不随着惯性参考系的变化而变化即不随着坐标系的选择而变化。它是依赖于时空间隔的长度ds或者世界线。
到这里，你就可以用狭义相对论的框架去解释双生子效应，因为哥哥的世界线长度发生了变化，他们之间再也不遵循时空间隔不变性，因此哥哥的固有时间发生了变化，所以回到地球比较的时候哥哥比弟弟要年轻。
这也就是说，上述的两个参考系之间再也不是平权等价的惯性参考系了。
因为我们找的不变量仅仅适用于两个相对运动的惯性参考系之间。
协变和逆变矢量：指标的位置不同命名，可能数学上会有更严谨的定义。
协变矢量：
逆变矢量：
协变和逆变张量与之类似，限于篇幅，不再多讲。
黑洞物理学
首先考虑最简单的史瓦西时空，
我们都知道，在广义相对论的框架中，物质的分布和运动影响时空结构，引力是时空结构的弯曲的几何表象，用度规张量描述。引力场的物理效果可通过黎曼几何中的几何量一一度规张量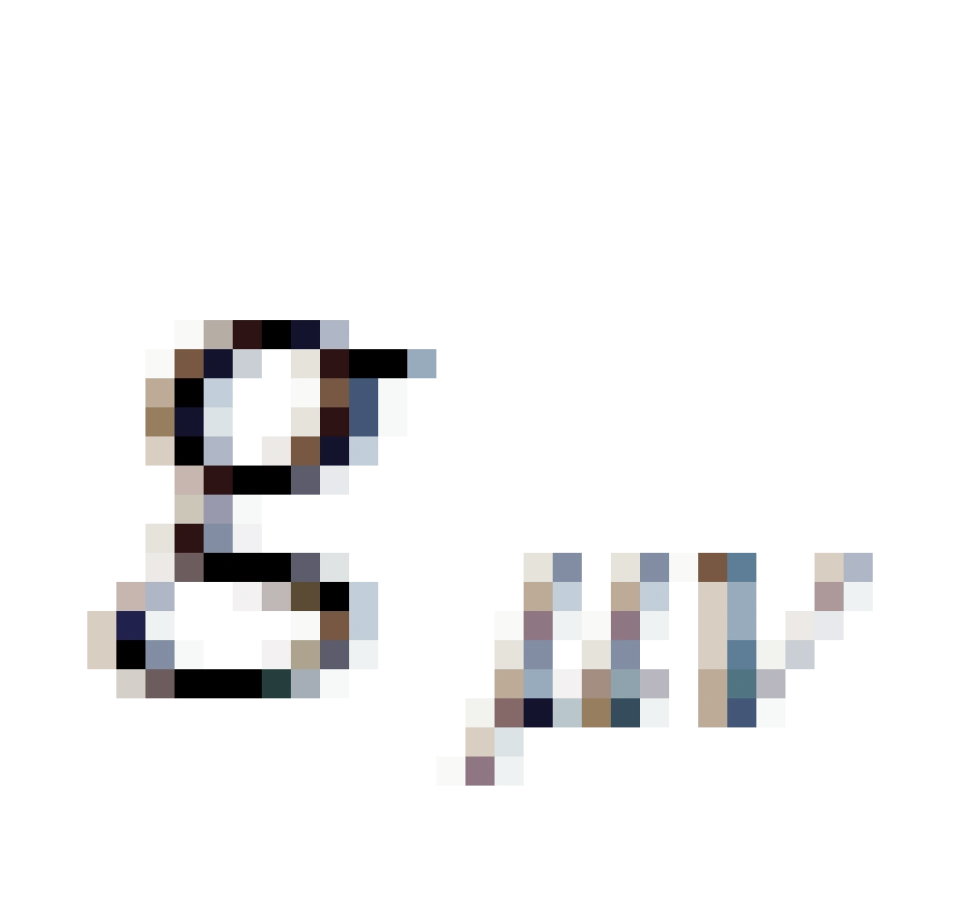
来体现。而物质的分布和运动用一个二阶张量来描述那就是能量动量张量。他是一个4×4的矩阵，有16个分量。包含能量流，动量流，能量密度还有三维空间中各个方向的应力/压强。
因此，描述引力相互作用的爱因斯坦引力场场方程的一端是描述物质场运动和分布的能量动量张量，另一端是反映时空结构变化的张量，而且以度规张量为函数。具体推导过程就不说了，直接写出爱因斯坦场方程。
爱因斯坦引力场场方程其实就是：
曲率项=物质项
其中，
被称为爱因斯坦张量（这里是不加宇宙项的）。
其中：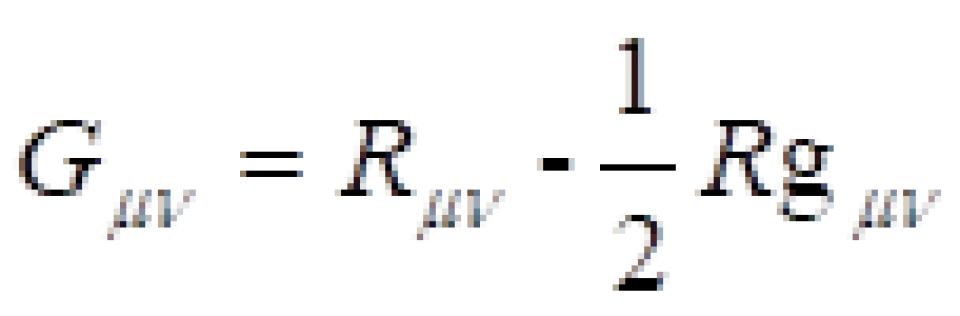
，这里每个都是4×4矩阵，有16个分量，由于它们是对称张量，k为系数， 
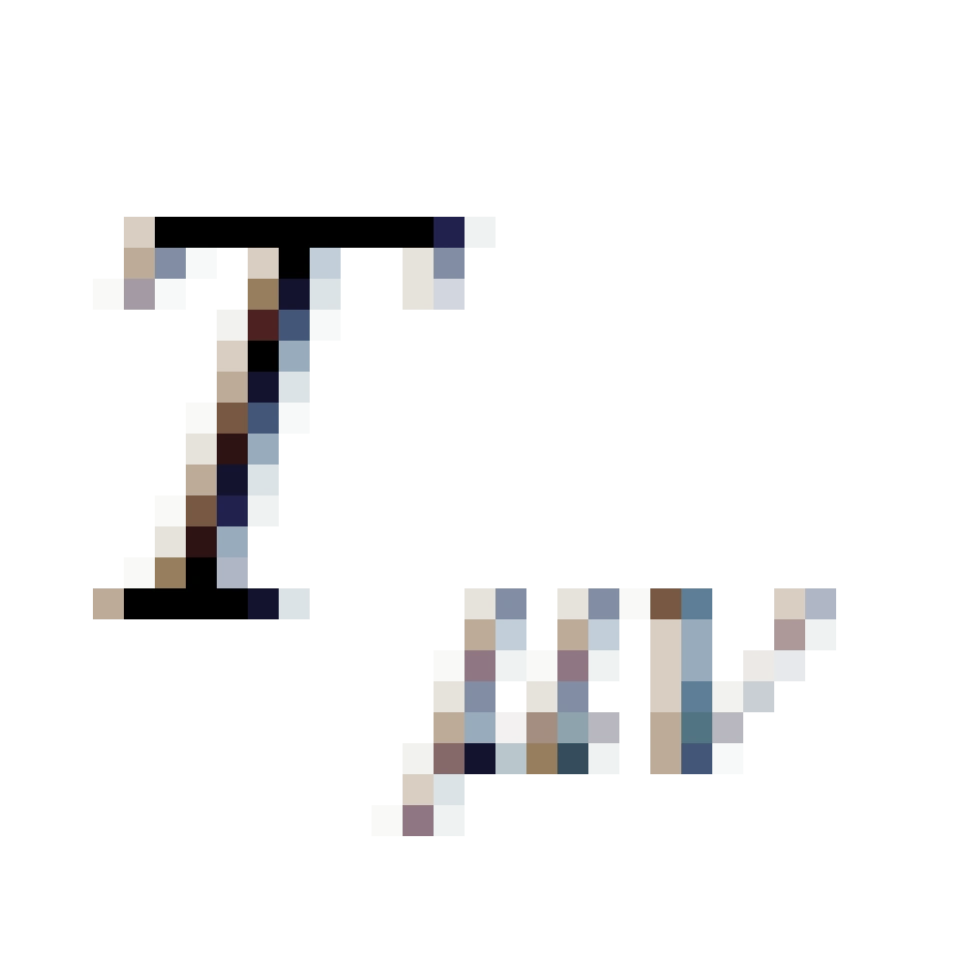是描述物质上的分布和运动的能量动量张量。 
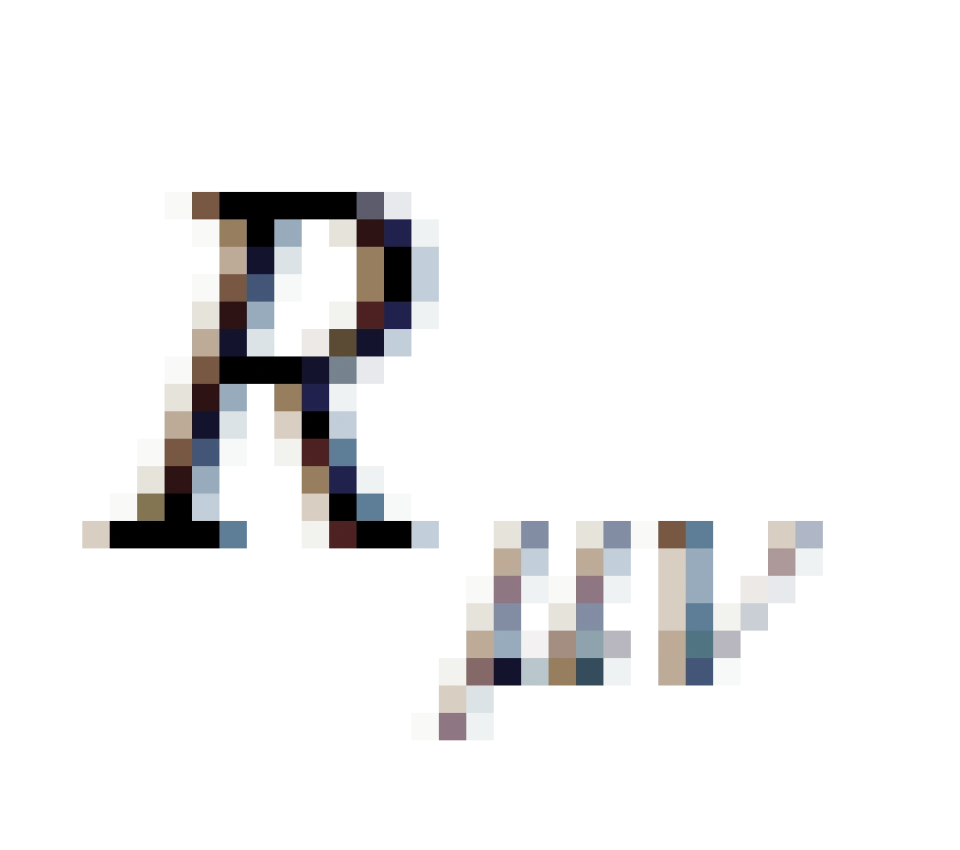被称为里奇张量，它是由四维黎曼曲率张量 
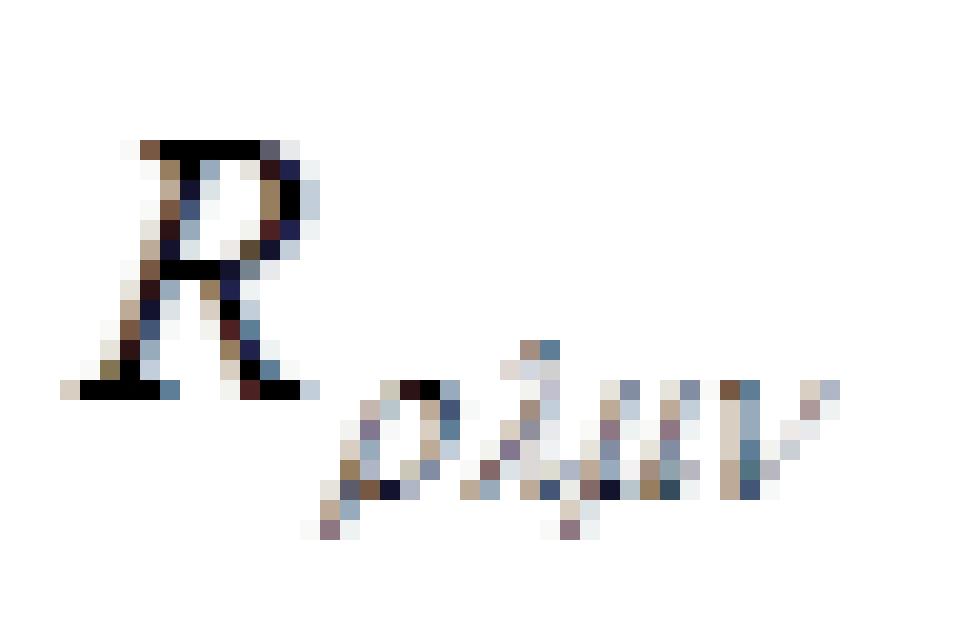缩并而来的亦即：
。
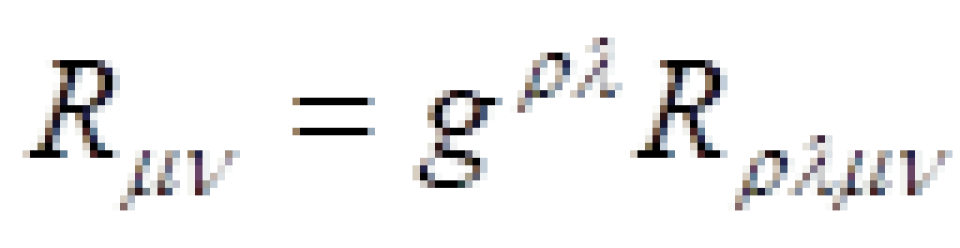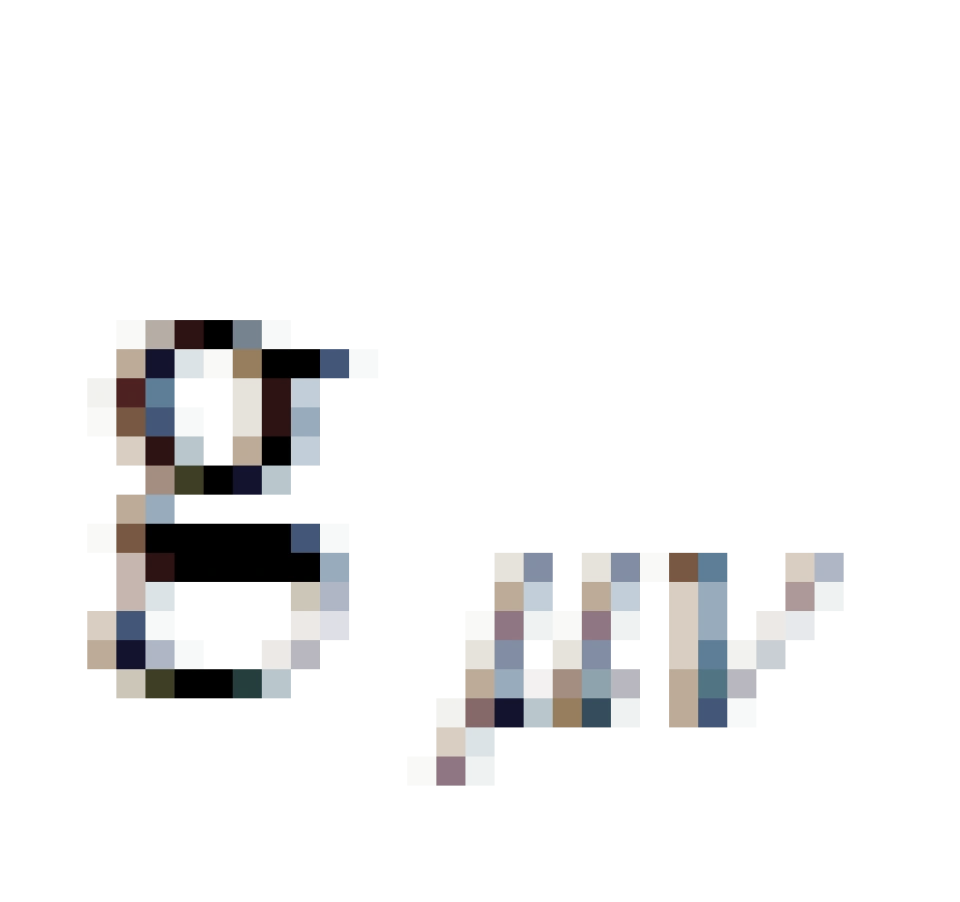就是我们前面说的度规张量，而R它叫做曲率标量，是由里奇张量缩并而来的亦即：
。
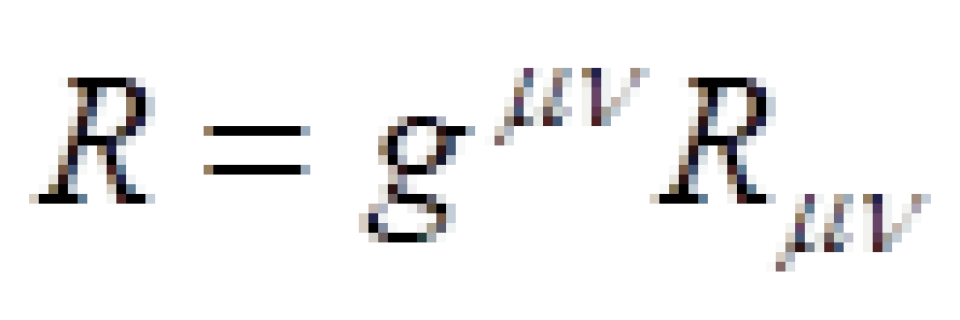张量缩并你就当做是一种矩阵求迹的扩展。一个二阶张量的分量用矩阵表示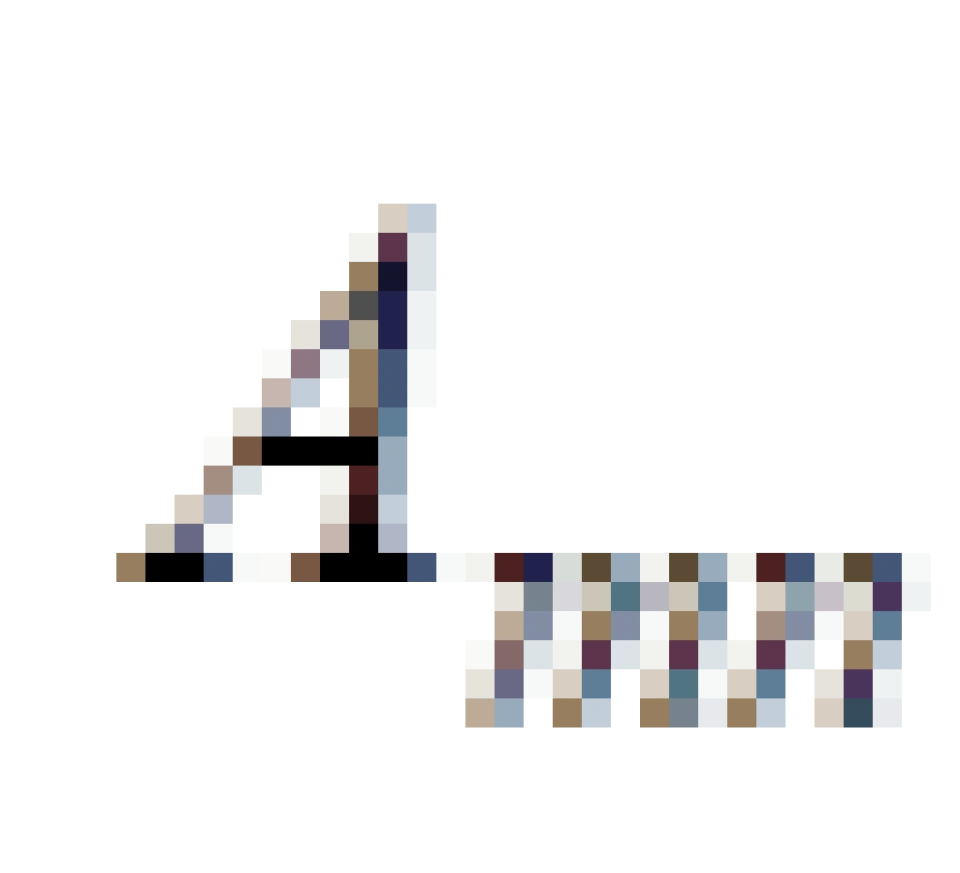 
表示，当m=n时，只剩下对角线上元素，所有对角线上元素的和就是迹，亦即是缩并为一个标量。迹，只在二阶张量也就是矩阵上有定义，它在高阶张量上的推广就是张量的缩并。
其实也不能理解，因为张量本身就是矩阵的高阶扩展。三阶张量缩并就是一个矢量，缩并后降两阶。
引力场的分布在广义相对论框架中，其实就是与度规场的分布有关，度规场其实是关于度规的一套分布函数，但该函数是由爱因斯坦场方程来确定的，由爱因斯坦场方程直接求出度规的分布函数，但是不能直接求出某时空点的度规。所以首先是由场方程接出对应的度规场函数，然后才能得到某点的度规。
当然有的时候爱因斯坦场方程很难求解(精确解)(万一考虑的外界条件不是球对称)，因为广义相对论场方程也就是爱因斯坦引力场场方程是由10个二阶非线性偏微分方程构成的方程组，应以确定10个决定时空几何性质的未知函数，也就是度规张量的10个独立分量。度规张量是4×4矩阵，一共有16个分量，但是由于度规张量是对称性的，因此，最后只有10个独立分量。对应着10个二阶非线性偏微分方程。这个方程组内还有4个恒等式，因此真正有用的独立方程只有6个。不过要想解方程，还必须引入4个跟坐标系选择有关系的微分方程，被称为坐标条件。这样加起来独立方程还是10个十个方程，十个未知函数，10个独立分量正好匹配。不过，如果想真正解微分方程，还必须有初始条件和边界条件。因此实际上去求解爱因斯坦引力场场方程是一件很困难的事情。
所以最后只有十个是独立分量。因此，这个方程实际上是十个联立的二阶非线性偏微分方程(度规张量的10个独立分量)，实际上很难解。解爱因斯坦场方程其实就是在求解度规场的分布函数。
不过可以考虑一些特殊情况，比如假设一颗天体没有自转，静态，它的引力场具有球对称性。有了这些限制条件就可以大大减缓难度，这样得出来的解。我们可以将直角坐标系的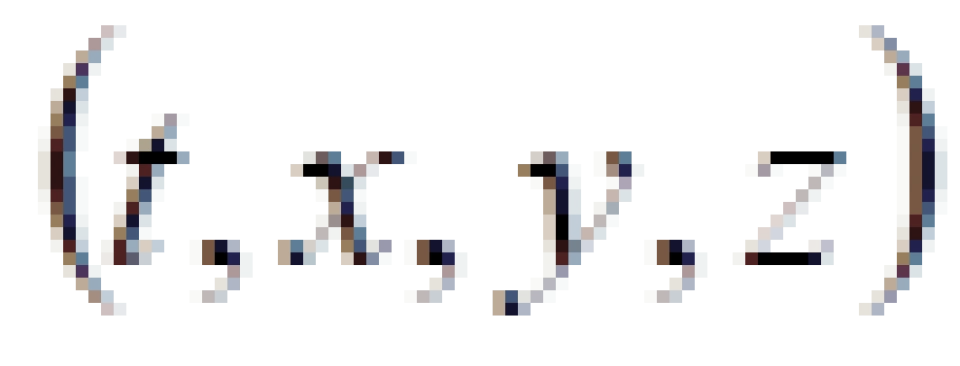
改成采用球坐标系
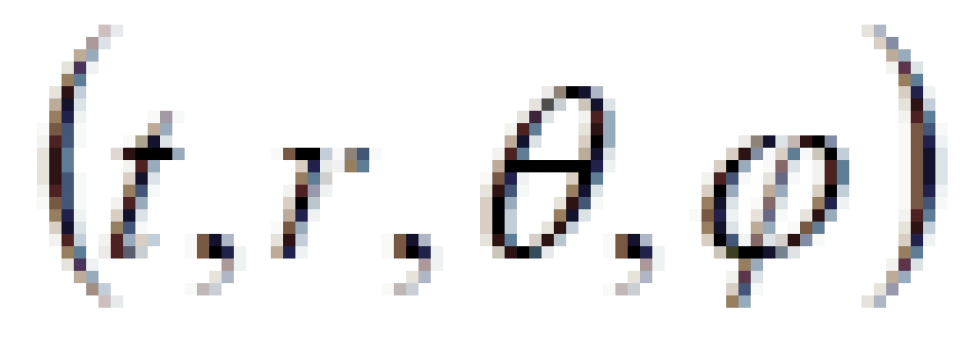，这样更容易看出球对称性。
这样我们将会得到一个应该是第一个最精确场方程的解一一史瓦西解。它是描述静态没有自转而且具有球对称性的时空。但是它分了两部分，就一种是天体内部的，还有一种是外部的真空解。
我们得到的球坐标系下的史瓦西时空的时空度规线元是这样的：
时间项分量的系数 
，当 
时，这一项分母将是零。
为了能看懂我们接下来要讲的，可能要介绍几个概念。
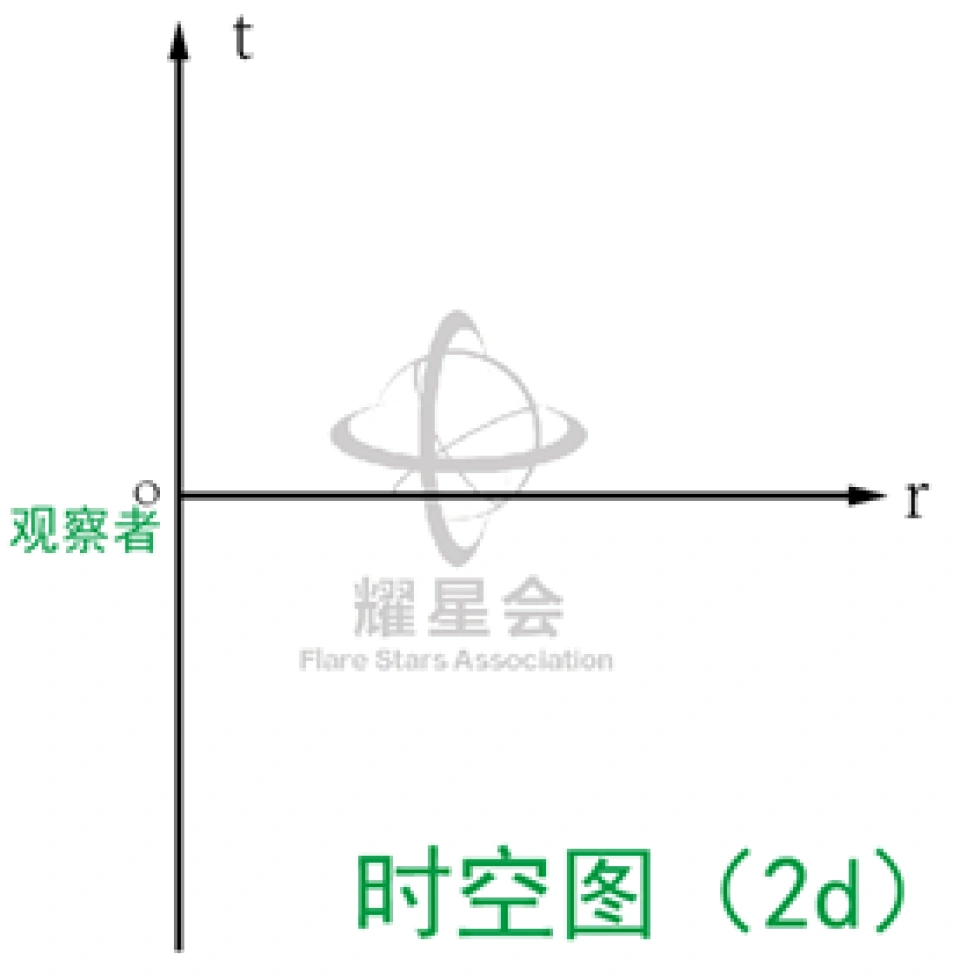
第一个就是时空图。
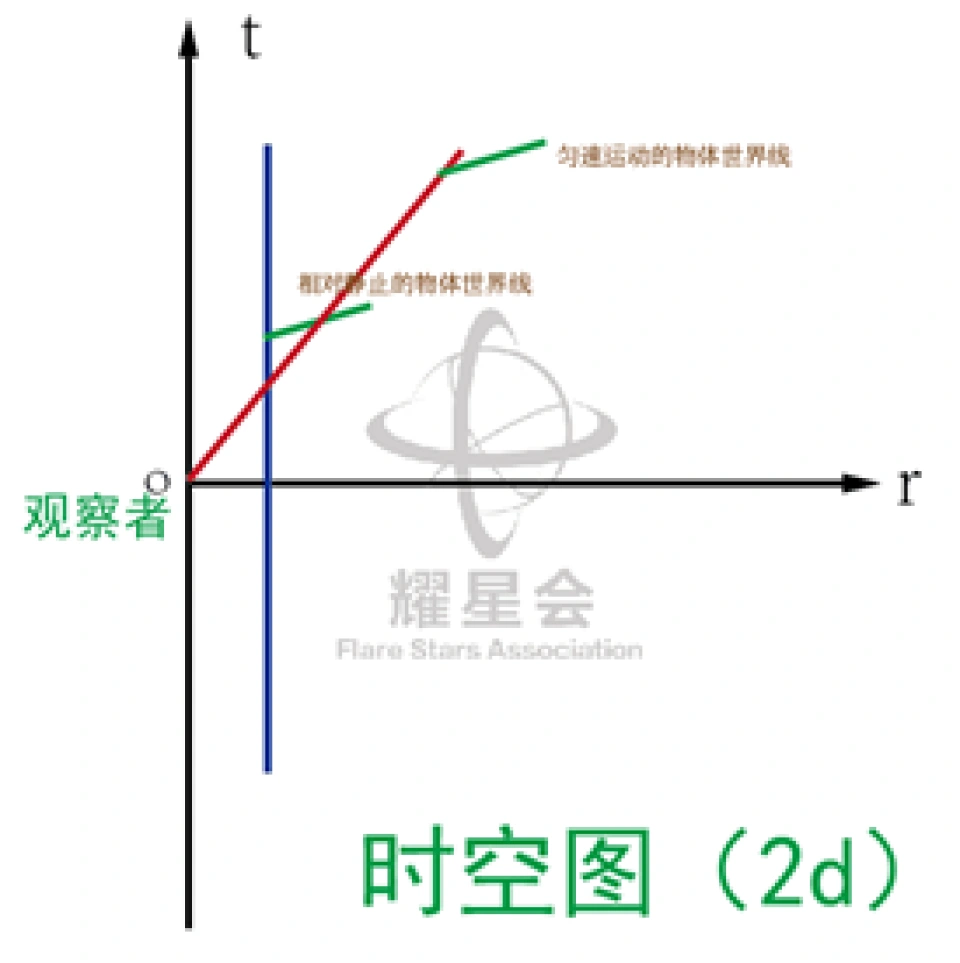
最简单的时空图就是横轴是空间，纵轴是时间
通常是以观察的自身为原点中心，每一点代表事件的时空位置。事件的轨迹代表的是世界线，或者是在时空的轨迹。
这两条线是相对于观察者本身相对静止的物体的世界线和相对于观察者相对运动（以某个匀速运动）的物体的世界线，如果是变速运动那么世界线将是一个曲线。
对于一个相对静止的物体，它的空间部分没有动，但它时间部分动了(因为时间是一直向着未来流逝的)。对于相对运动的物体，它的空间部分在走，时间部分也在走。
斜率就是物体相对于观察者的运动的速度。
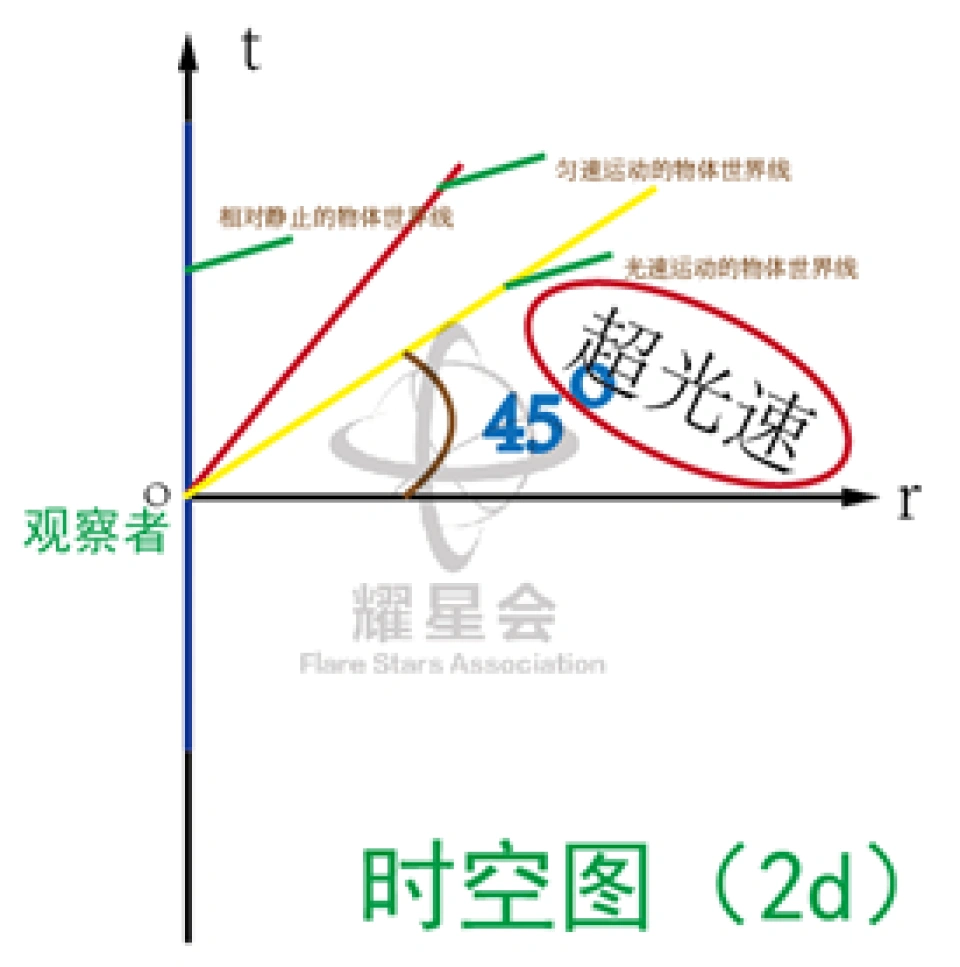
这里有一个特殊的地方，也就是45度的时候，斜率是1。
这其实是光走的路，
因为光速不变，所以我们可以令c=1
t轴其实在物理上是ct，
还记得 
吗？
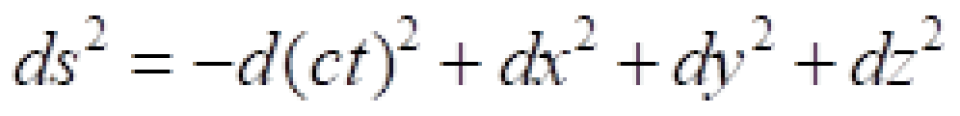这个才是原来样子。数学上可以直接加减，但是物理上运算要考虑量纲，所以采取的方法就是时间空间化，时间坐标乘上一个带有速度量纲的东西，但是这个东西最好要固定，不随参考系的选择而变化。因此，光速很明显是个合适的任选者。
这个四维坐标是ct。乘上c是没有关系的，因为光速不变。
所以其实这个时空图纵轴是ct。如果令c=1，那么竖轴的写成t了。
顾名思义这种单位就叫做几何单位制。
这条45°斜直线就代表了光子的世界线，任何小于光速运动的，世界线就在上面，大于光速的就在下面，靠近r轴。
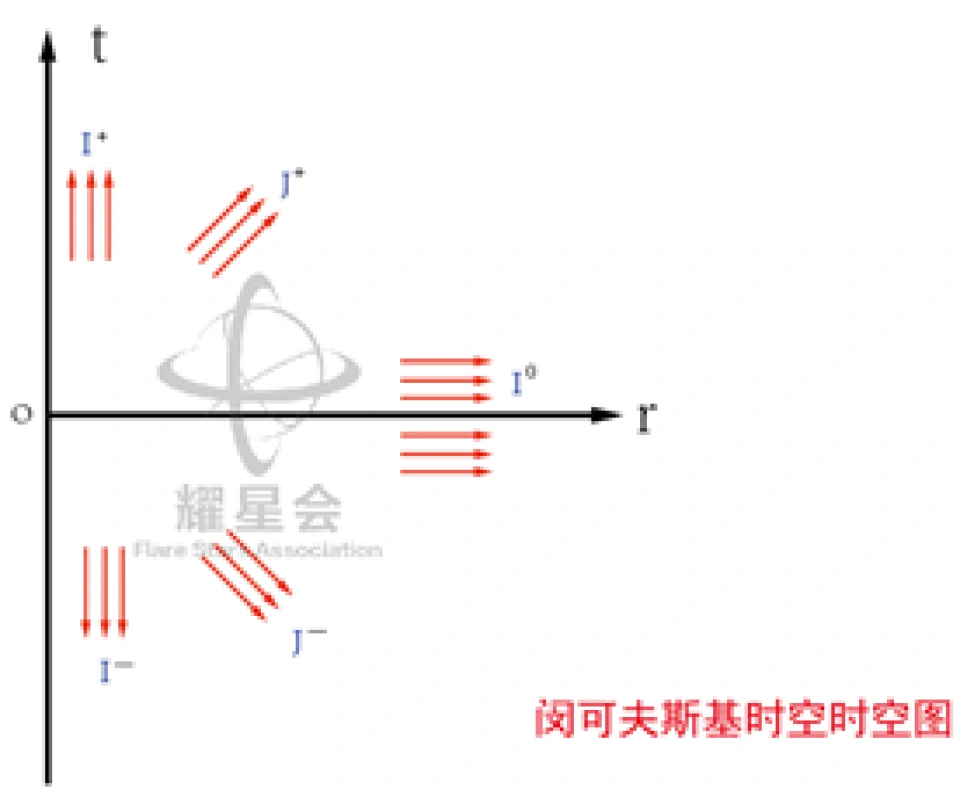
说完时空图，我们介绍闵可夫斯基时空的时空图。
众所周知，物理上，四维微分流形附带洛伦兹型度规就是时空。洛伦兹型度规就是4×4矩阵，其对角元一正三负或者一负三正，对角元之和就是号差，为+2或者-2。
因此，闵可夫斯基时空就是四维微分流形附带闵可夫斯基度规亦即：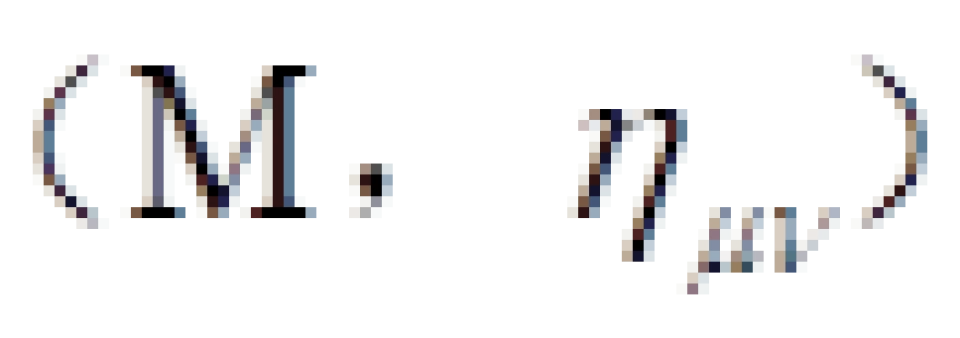 
闵可夫斯基度规为：
闵可夫斯基时空时空线元为：
我们采用球坐标系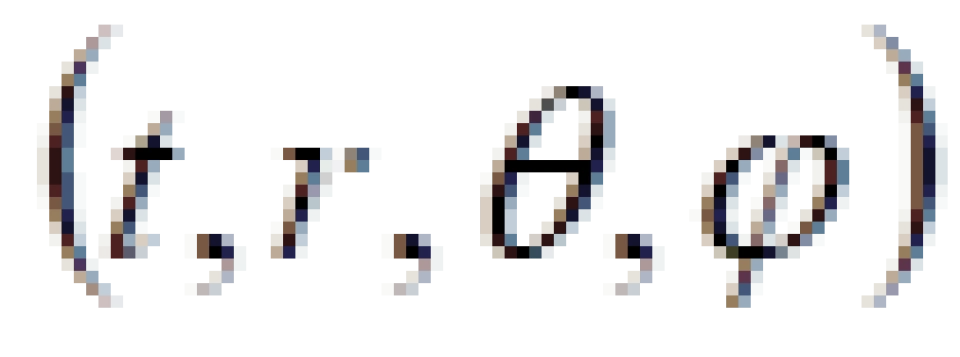
，上面在直角坐标系
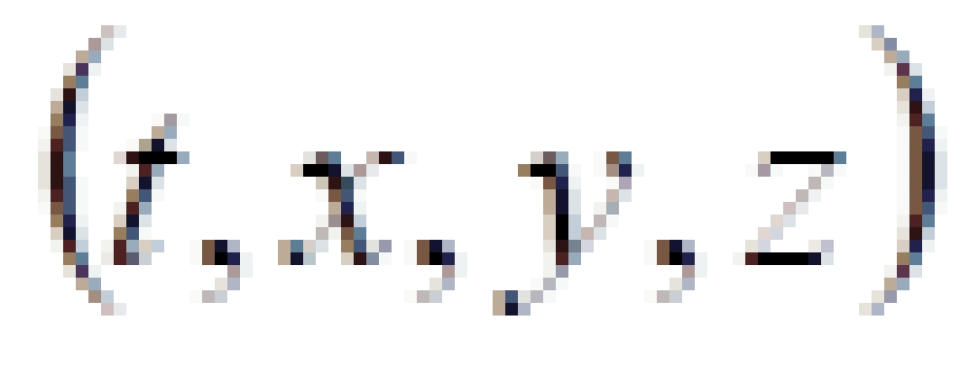上中闵可夫斯基时空线元改为：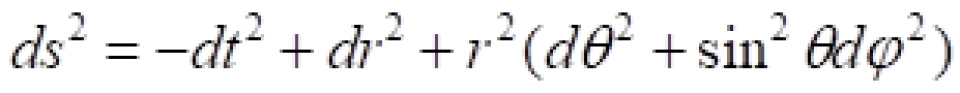
后面那串 
就不看它了，只考虑t与r。
为了方便，
下面也就不写了。
现在我们来看看闵可夫斯基时空的时空图长啥样子。
我们就来介绍一下这几个字母分别代表什么意思？
t是时间，r空间坐标。
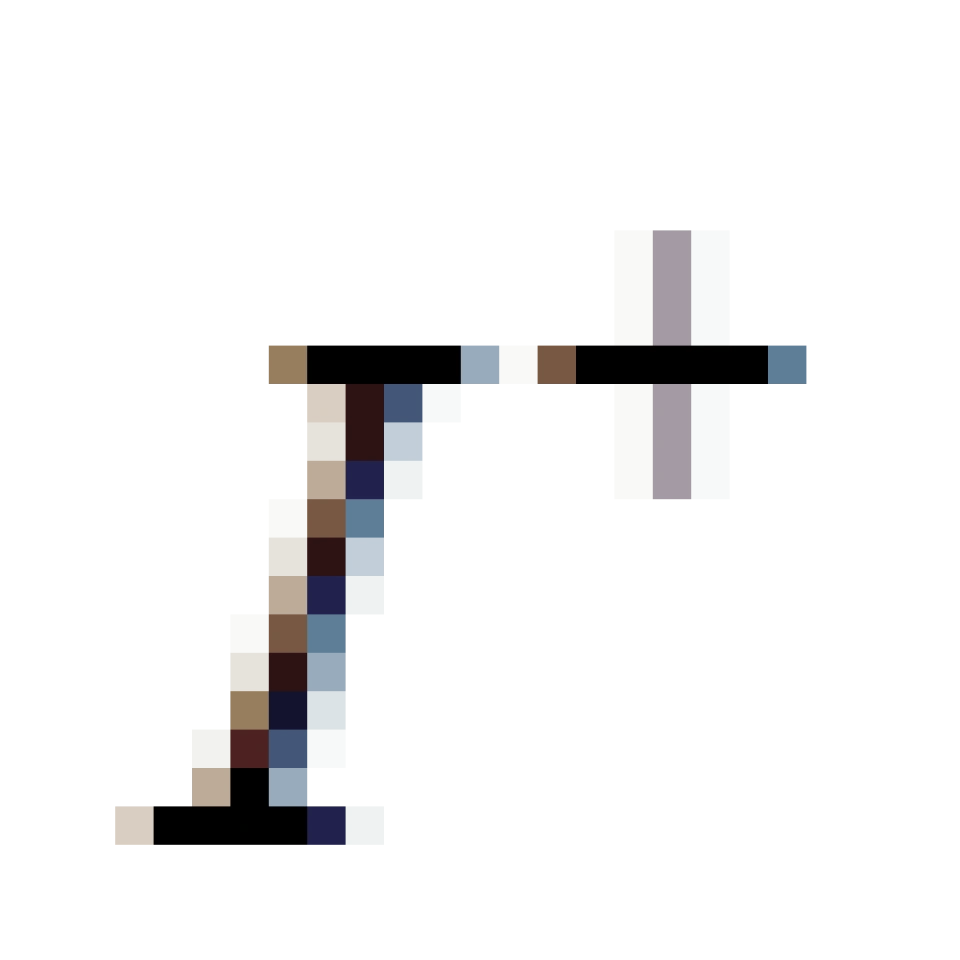，代表的是，对于r取任意一个有限值时，t趋于正无穷大。它是所有类时世界线( 
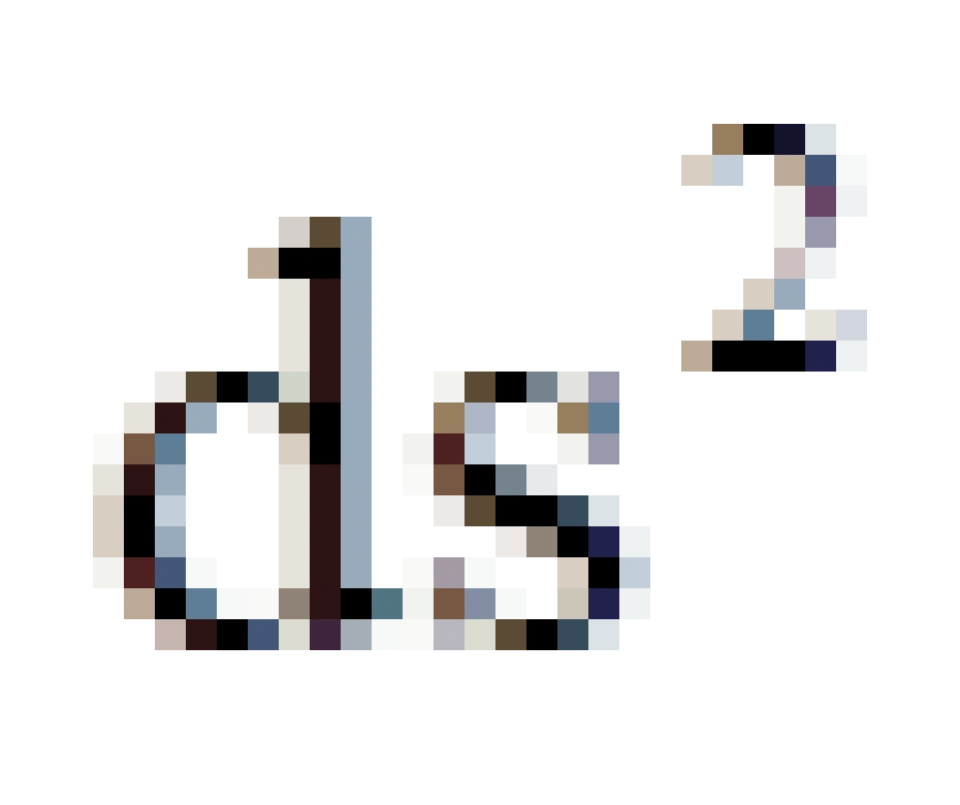<0)延伸的区域， 
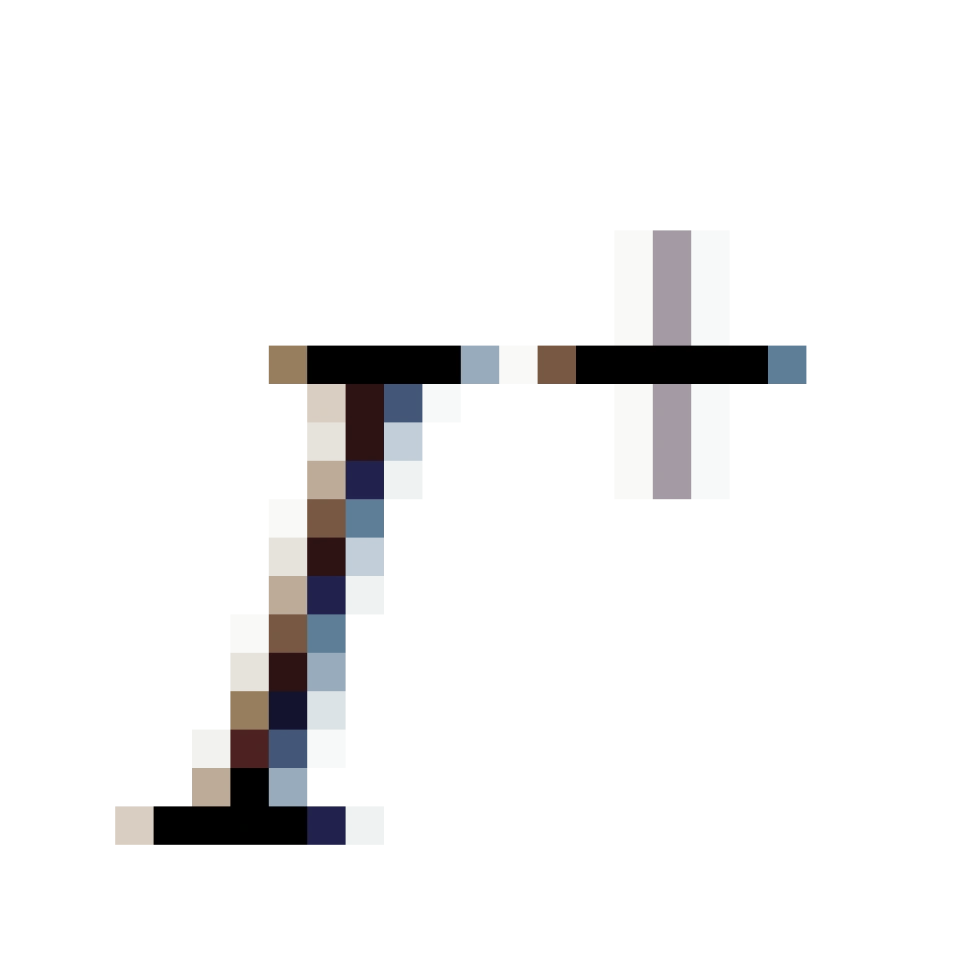，被称之为类时未来无穷远。
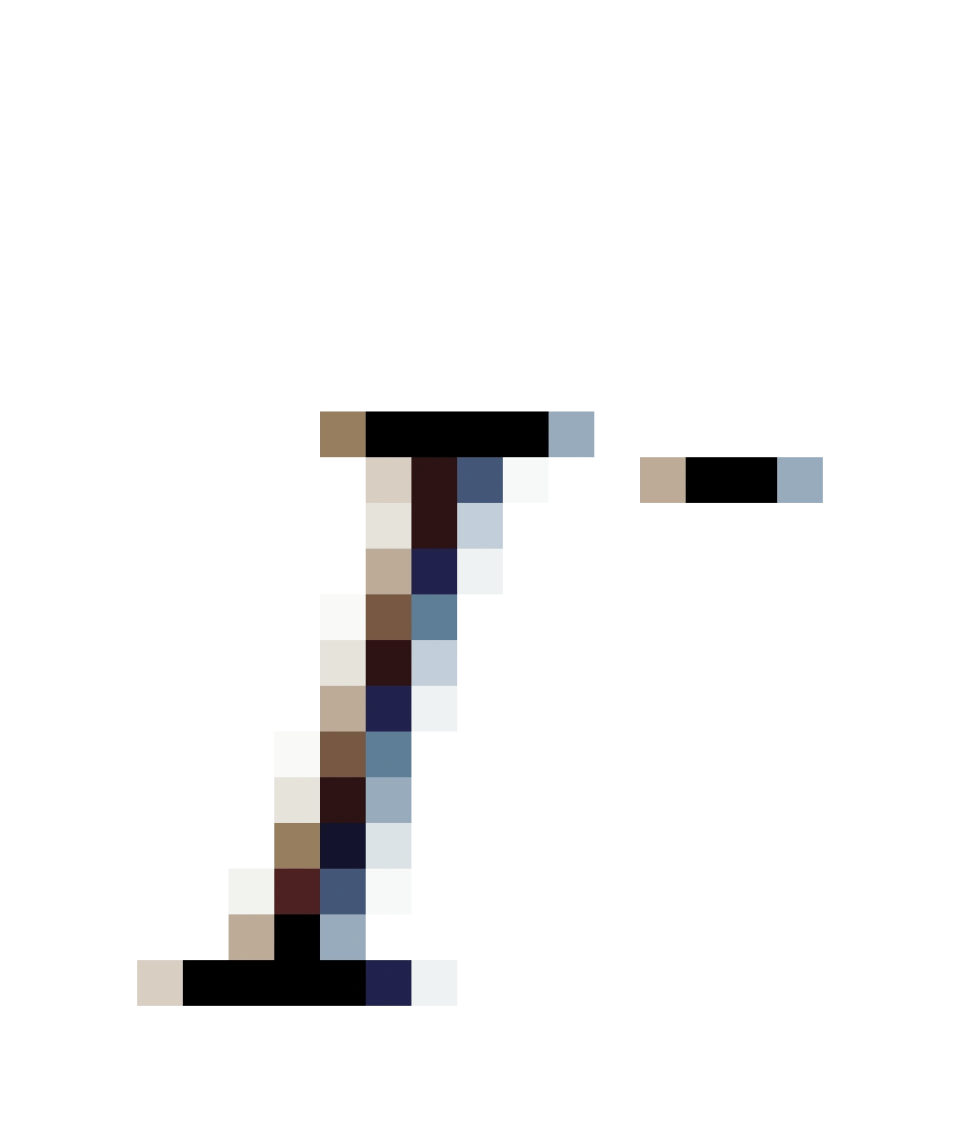，代表的是，对于r取任意一个有限值时，t趋于负无穷大，它是所有类时世界线( 
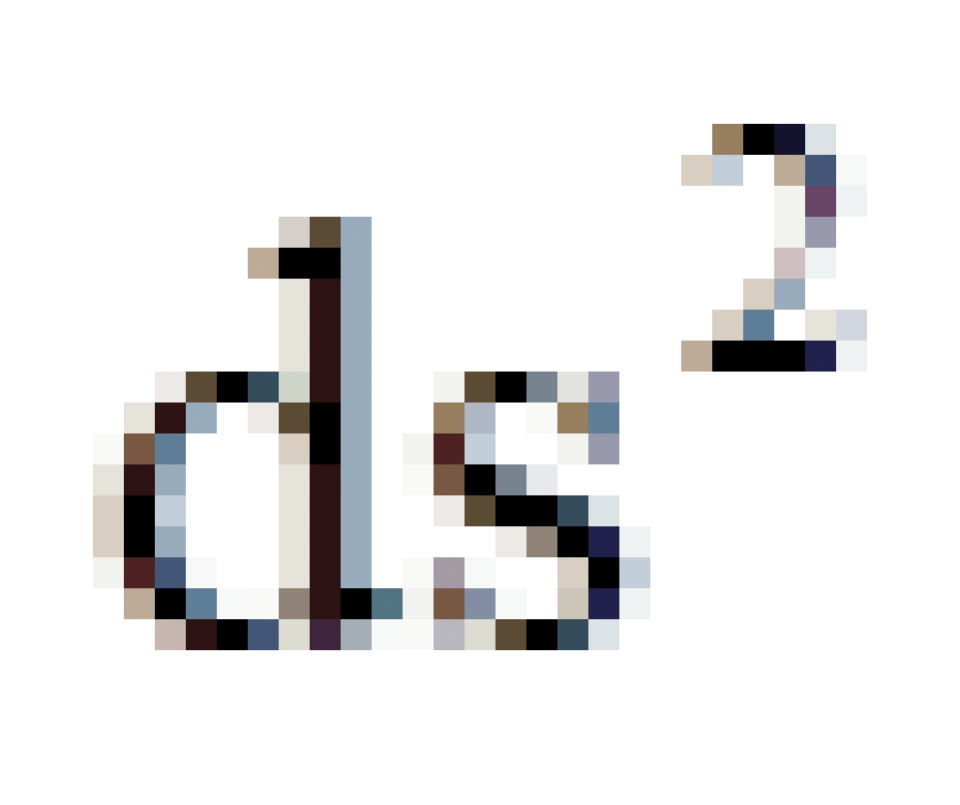<0)延伸的区域， 
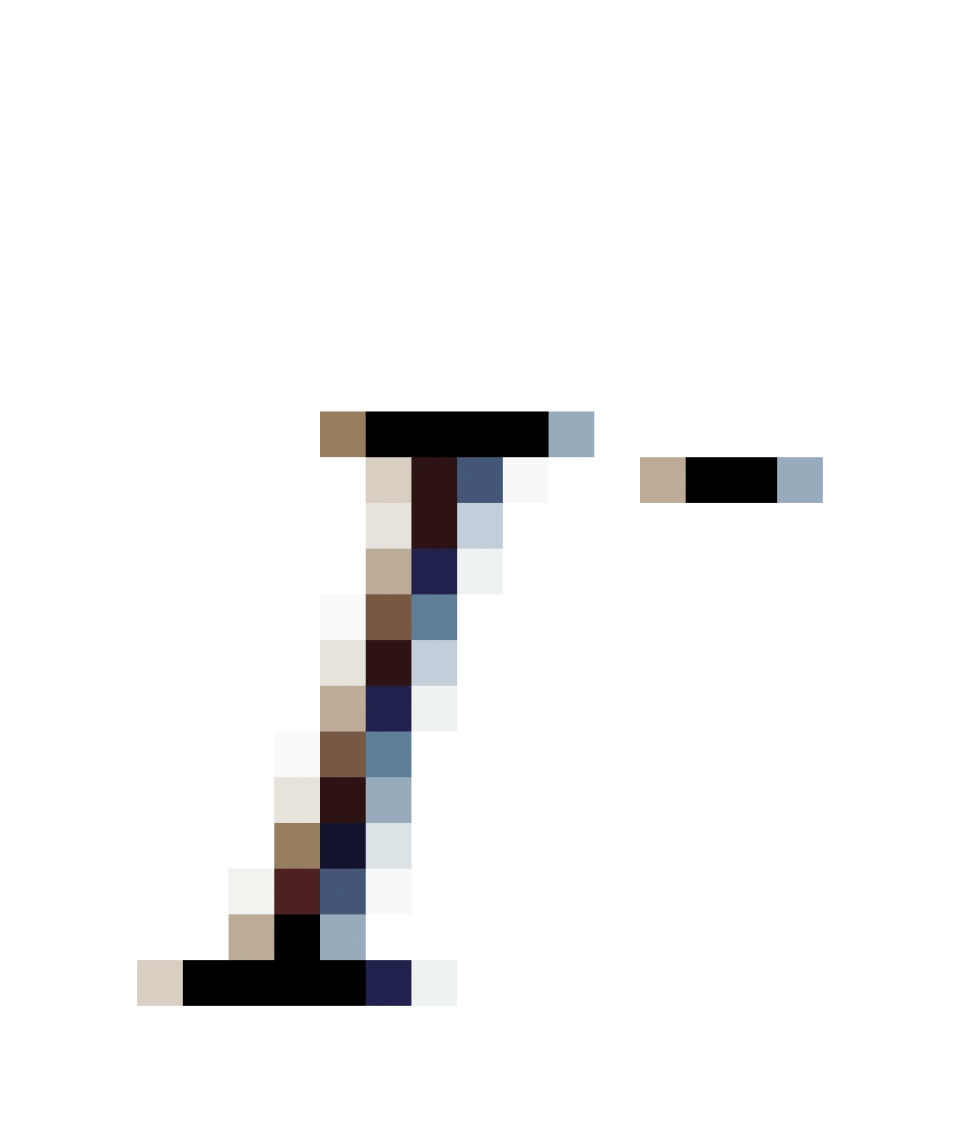，被称之为类时过去无穷远。
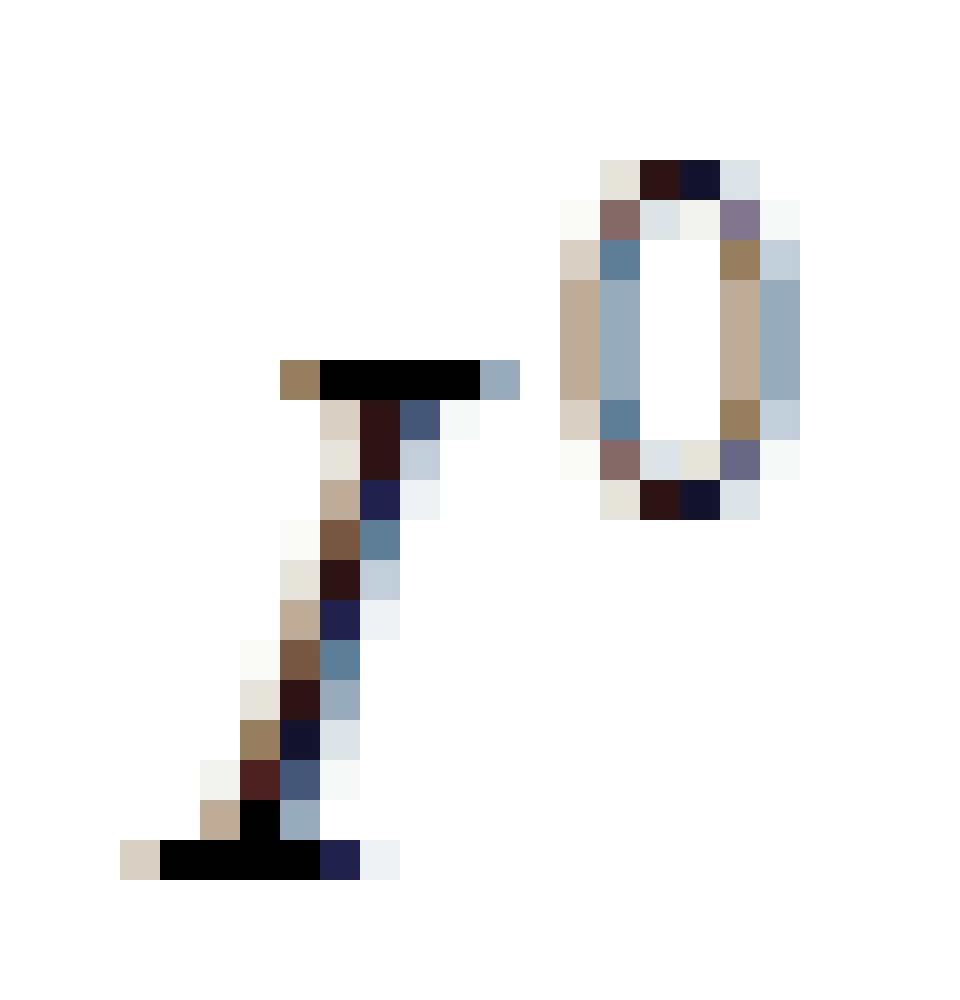也就可以理解了，它是对于t取一个有限的值，r趋于无穷大时，所有类空世界线( 
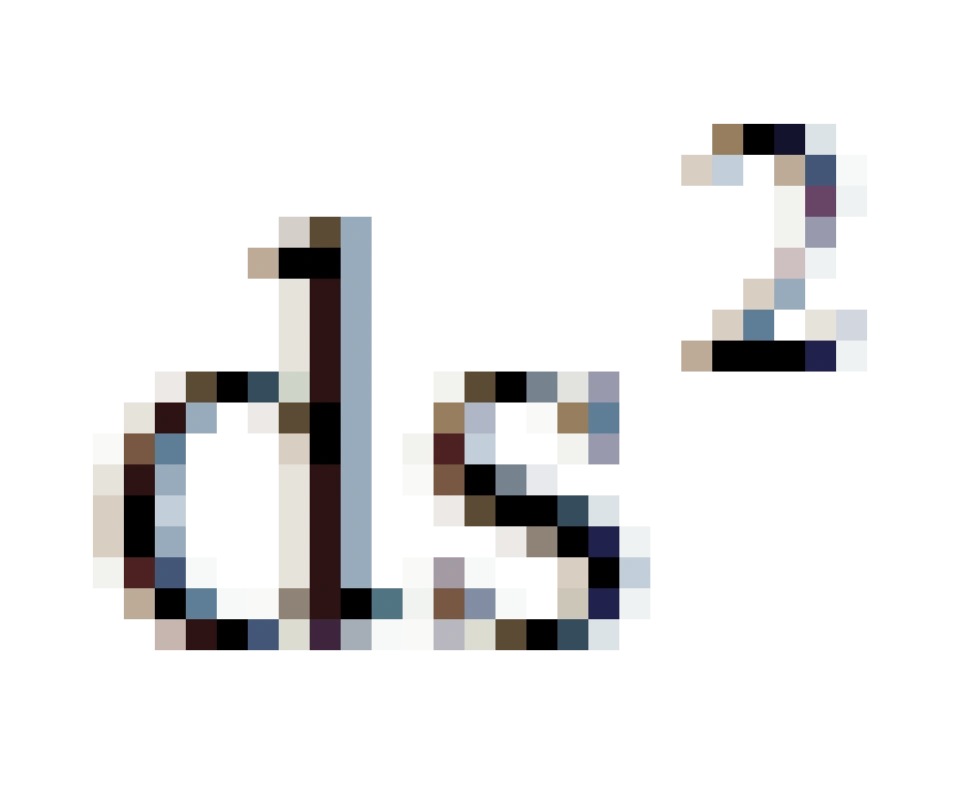>0)延伸的区域，被称之为类空无穷远。
剩下两个花体字母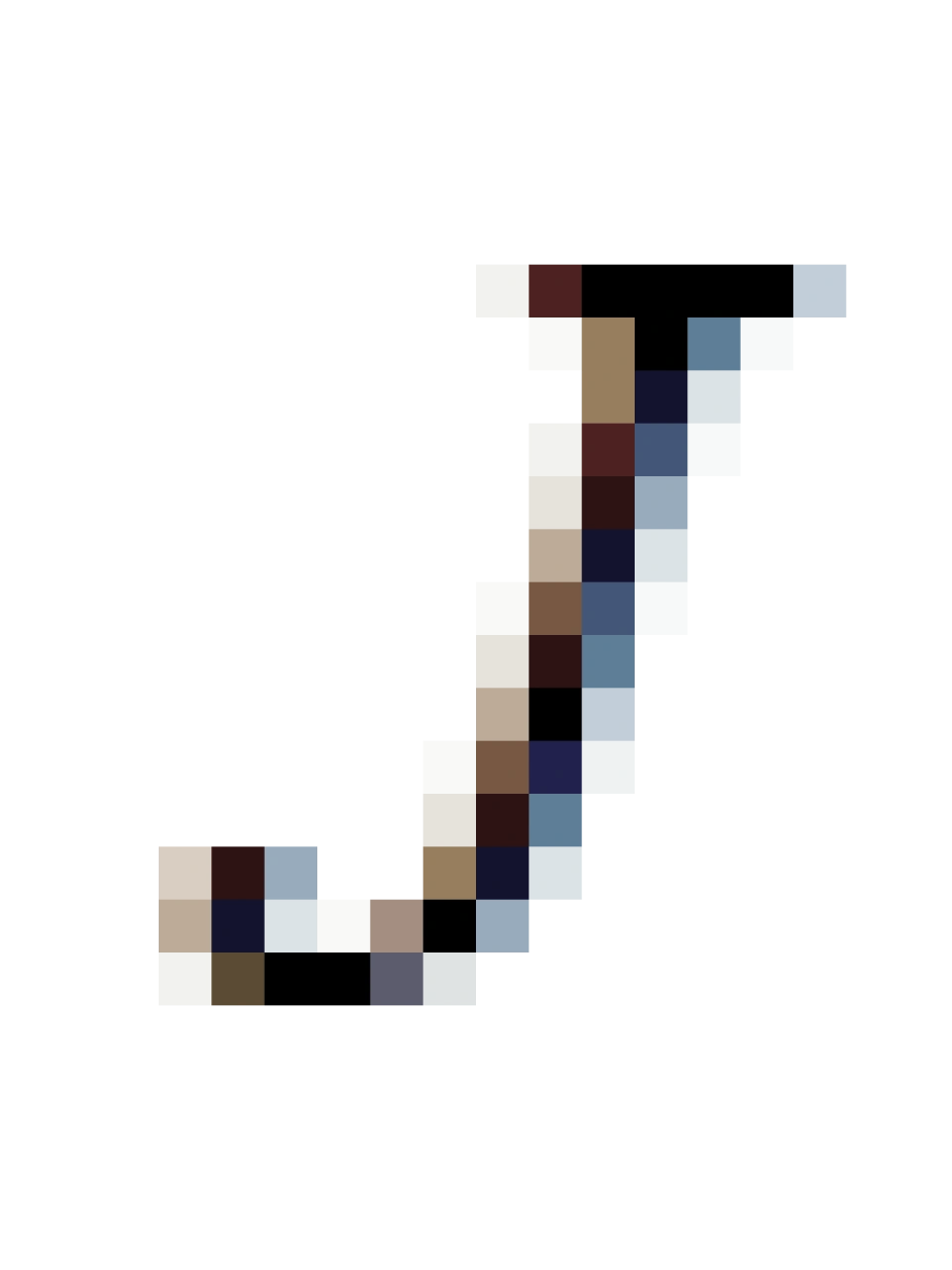
，跟代表的类时世界线的
,
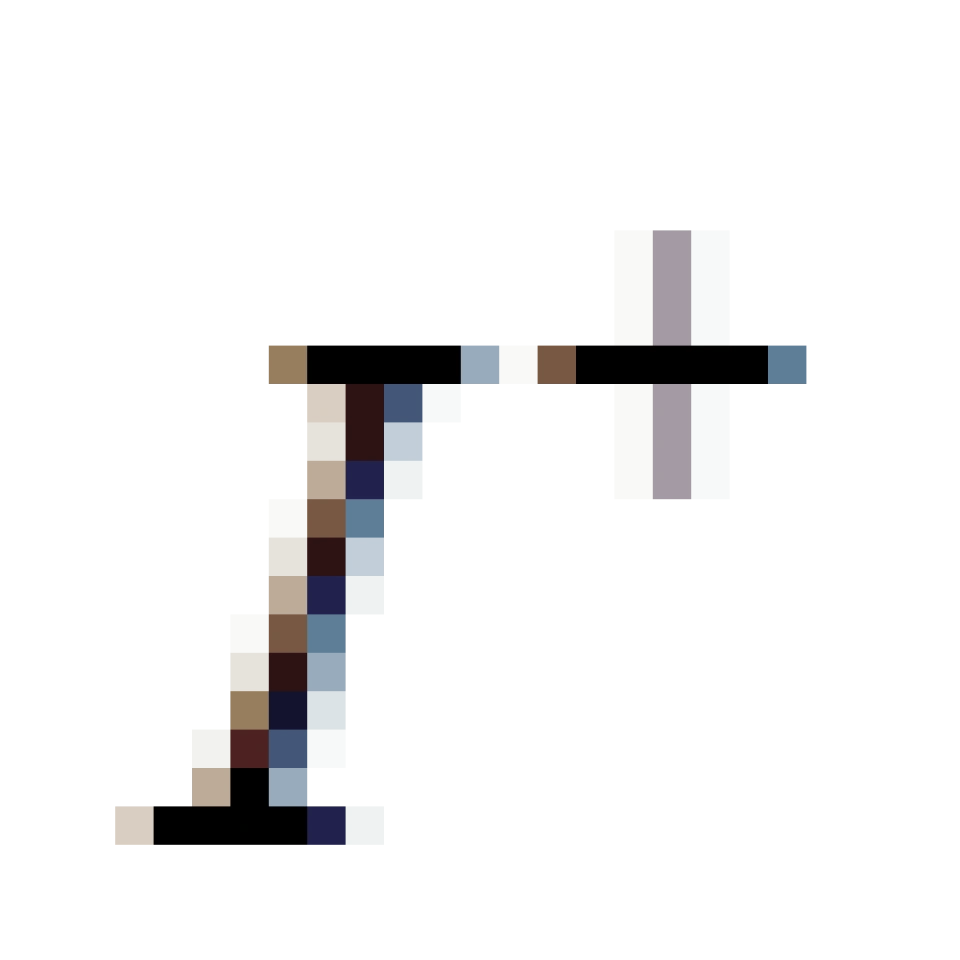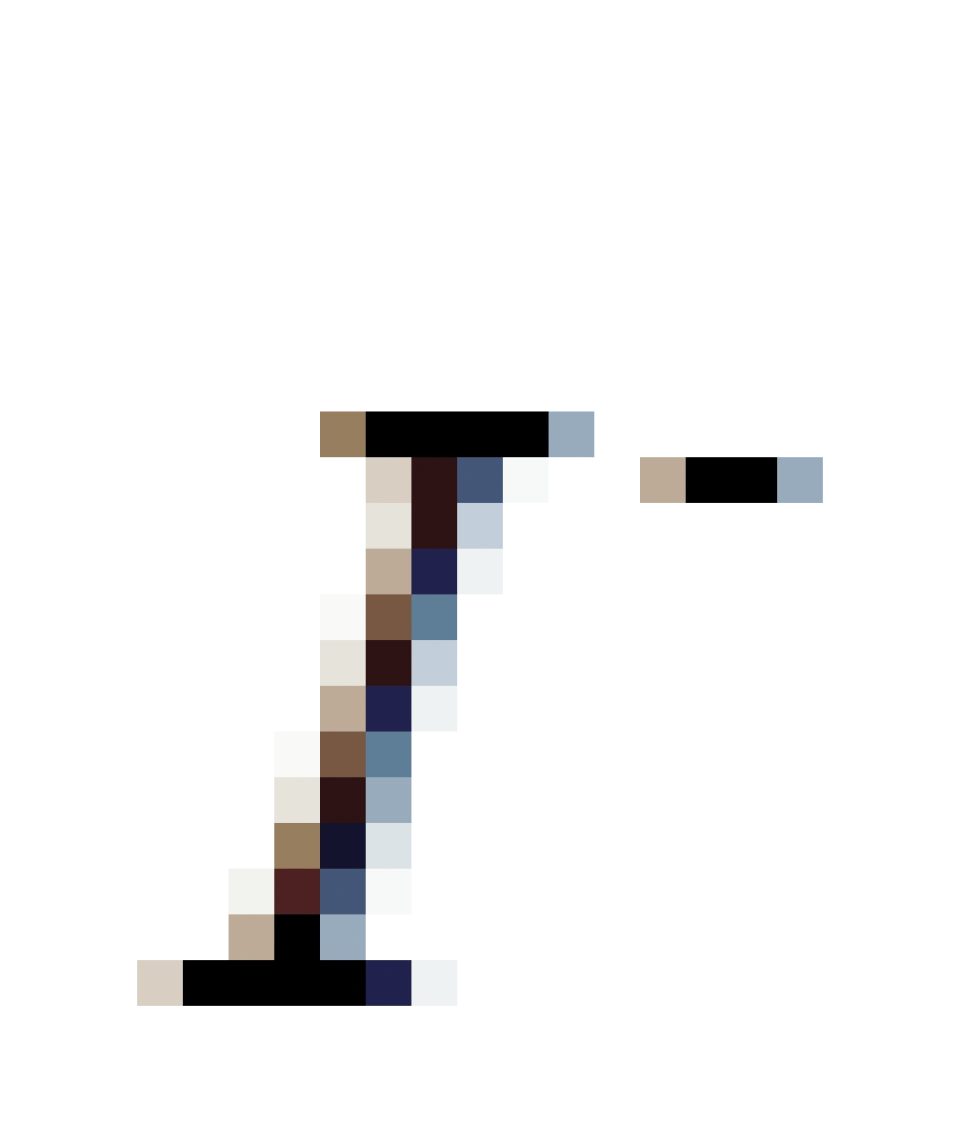一样，不过它代表的是所有类光曲线(
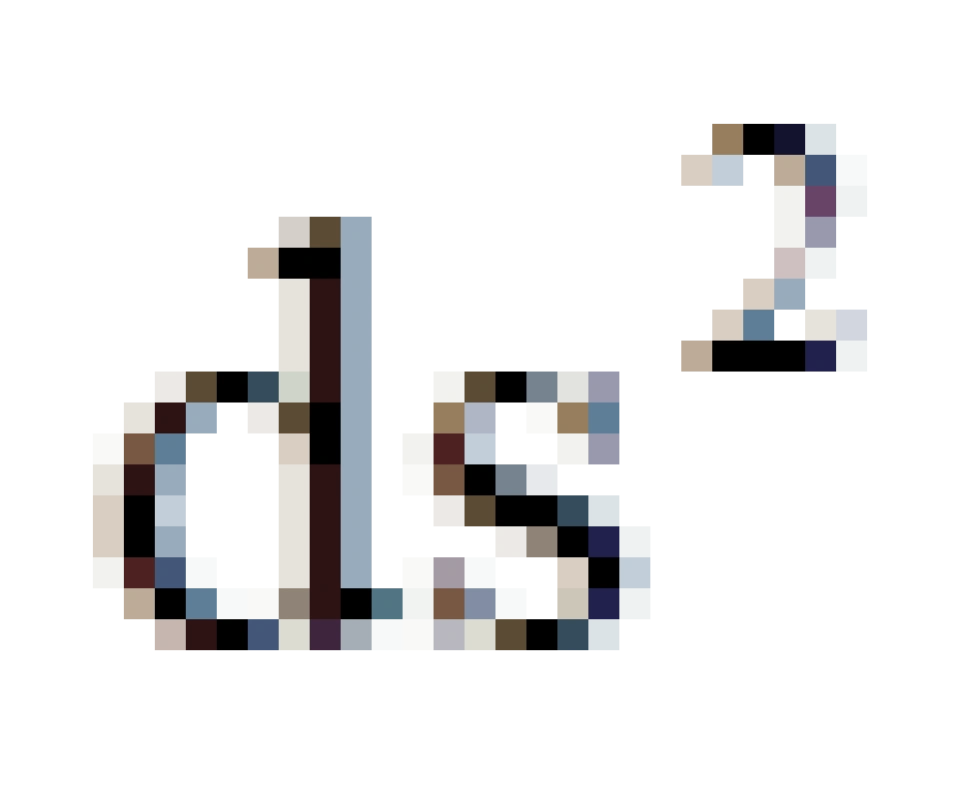=0)延伸的区域，也就是运动速度到达光速时候的世界线延伸的区域。
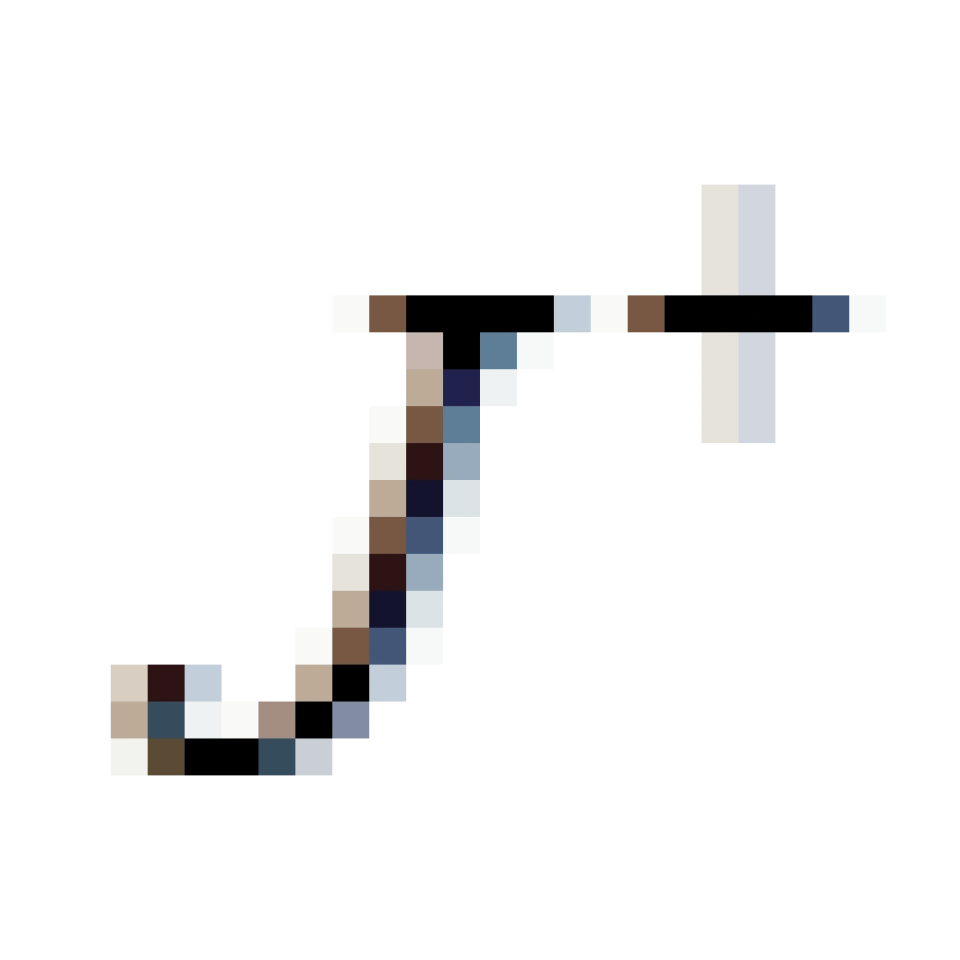是（t-r）取的是有限值，t+r趋于无穷大，所有射出的未来类光世界线的区域,被称之为类光未来无穷远。
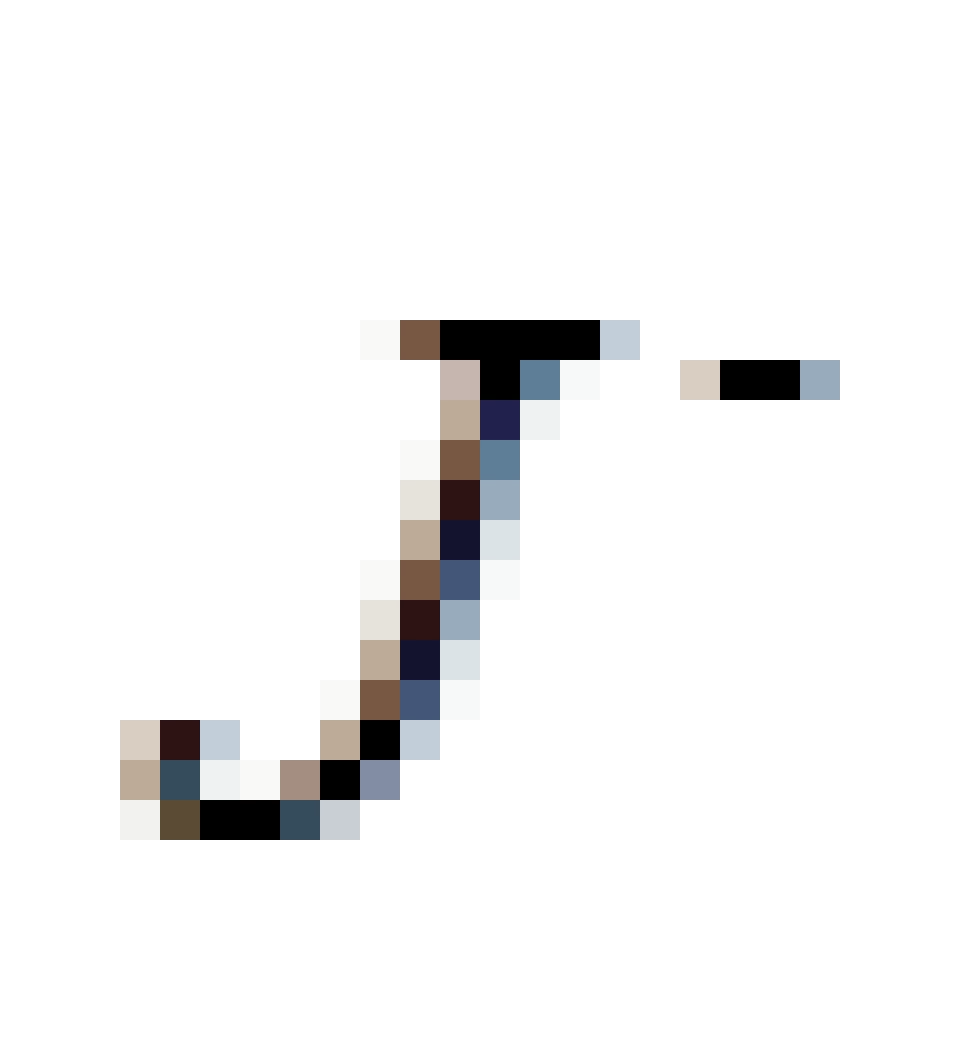是（t+r）取的是有限值，t-r趋于无穷大，所有射入的过去类光世界线的区域,被称之为类光过去无穷远。
但是其实这些无穷远点(空间上的还有时间上的)在这图上面表达不出来，并且这个无穷远并不是某一个无穷远处点，也不是某个时空区域。它代表含义是某个时空点变动趋势的概念(比如，类时无穷远就是当r取有限值，t趋于无穷大)，所以你在时空图上没办法说哪块区域或哪个点，就代表这个无穷远点。而且当我们用时空图去描述有引力情况下或者是黑洞附近时空情况时候，我们会发现光线的世界线会弯曲，也就不会保持45度角。
于是有人就想把这些无穷远点压缩到一个有限的距离，距离越远越趋近于0，那么当趋于这些无穷远时就是趋于0，并且能够保光锥45度(类光世界线45度夹角)。
于是彭罗斯图就出来了。它究竟是怎样的，我们下期介绍。
未完待续……
【本文为耀星会的原创作品，未经允许，禁止盗用、转载、篡改文章，否则耀星会将追究版权责任。】
