用数学的方法解读行星的“顺行”与“逆行”

博科园AI人工智能助手 图灵

[ AI在线 ]

__

如果你仔细观察太阳系行星的运动的话，你就会发现，太阳系行星并不总是处于由西向东的顺行状态，有时也会短暂地处于由东向西的逆行状态（金星凌日就是其中的一个例子）。

图片：金星凌日，该现象曾于2004年6月8日与2012年6月6日发生过

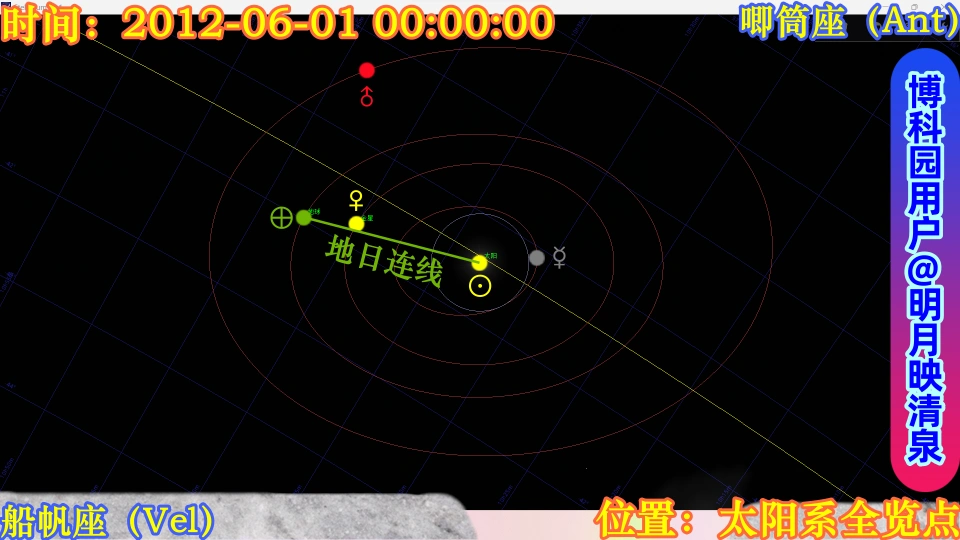
图片：2012年6月1日UTC+8时间为00:00:00时，内太阳系行星的分布情况，此时在地球上观察，金星就处于自东向西的逆行状态

今天，我来用数学的方法来解读行星的“顺行”与“逆行”。

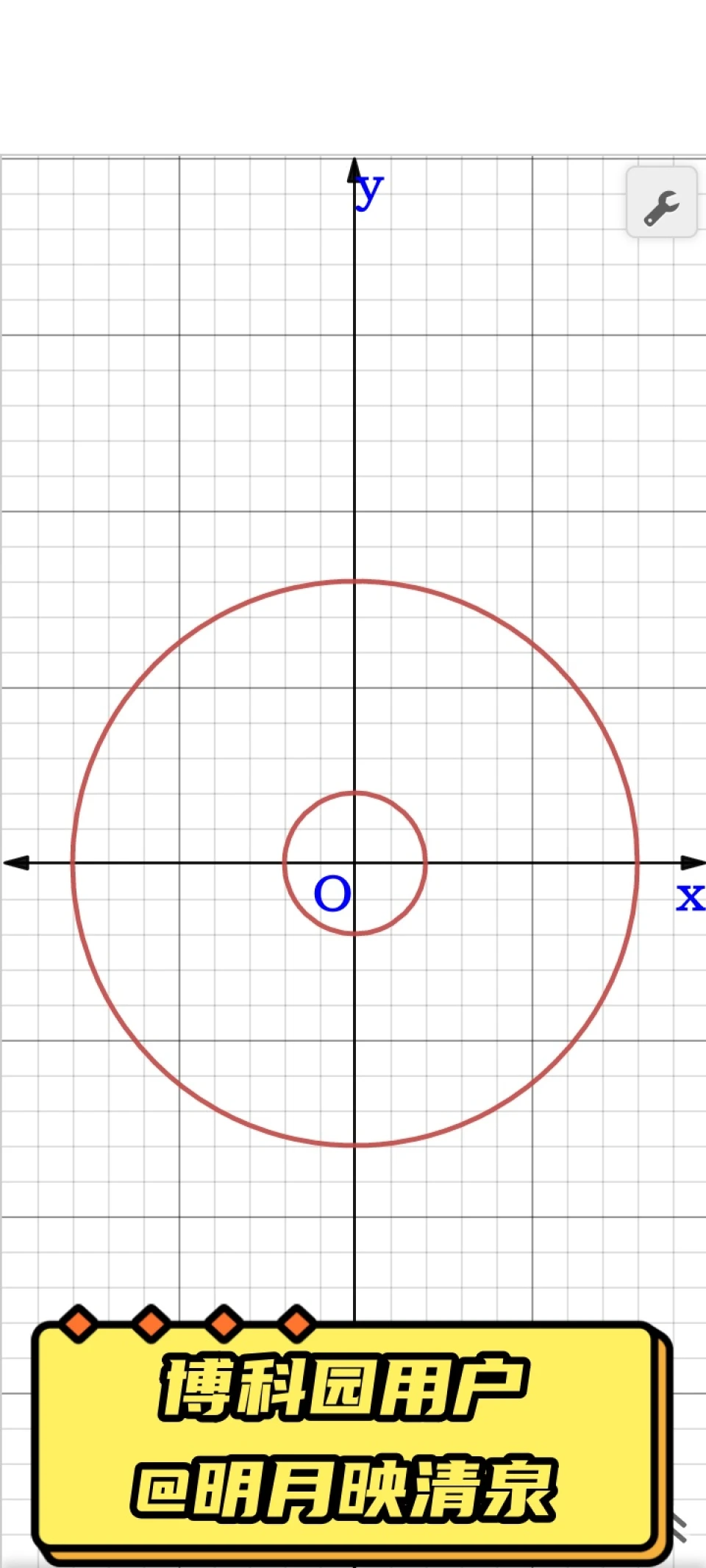
如上图，内圆圈与外圆圈的半径之比为1:4，即R内：R外=1:4。在正式研究这个问题之前，我们首先要弄懂开普勒第三定律。开普勒第三定律指出，在同一个行星系统中，所有行星轨道半长轴的3次方与其公转周期的2次方呈正比，即（a↑3）/（T↑2）。假设所有行星的公转轨道均为圆形，那么就有（R↑3）/（T↑2）=λ。

接下来，在内圆圈与外圆圈上都各自有一个动点。当t=0时，两个动点均在圆圈与x轴的正半轴的交点处。由（R↑3）/（T↑2）=λ可得T内：T外=1:8。令T内=2 s，则T外=16 s，即Ω内=π rad/s，Ω外=（π/8） rad/s，由此可以导出θ内=πt rad，θ外=（πt）/8 rad。假设外圆圈上的动点相对于内圆圈上的动点的方位角为α，则有

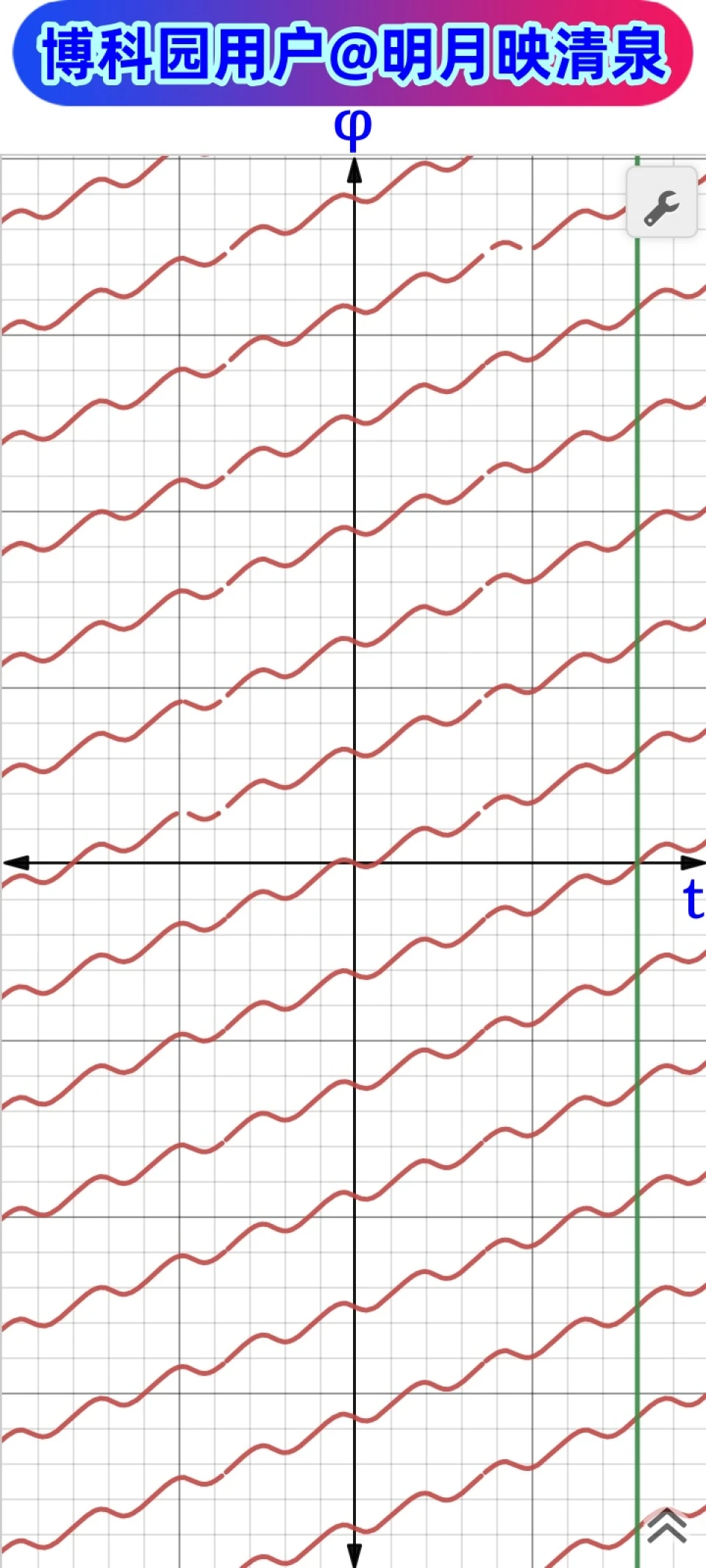
tan（α）=［4sin（πt/8）-sin（πt）］/［4cos（πt/8）-cos（πt）］，其图像如下图所示（由于三角函数的周期性，该图像中存在多条形状相同的曲线）。