博科园AI人工智能助手
图灵
以上是一个阻尼振动的二阶微分方程
1.下面是Mathematica求解二阶微分方程NDsolve部分的代码
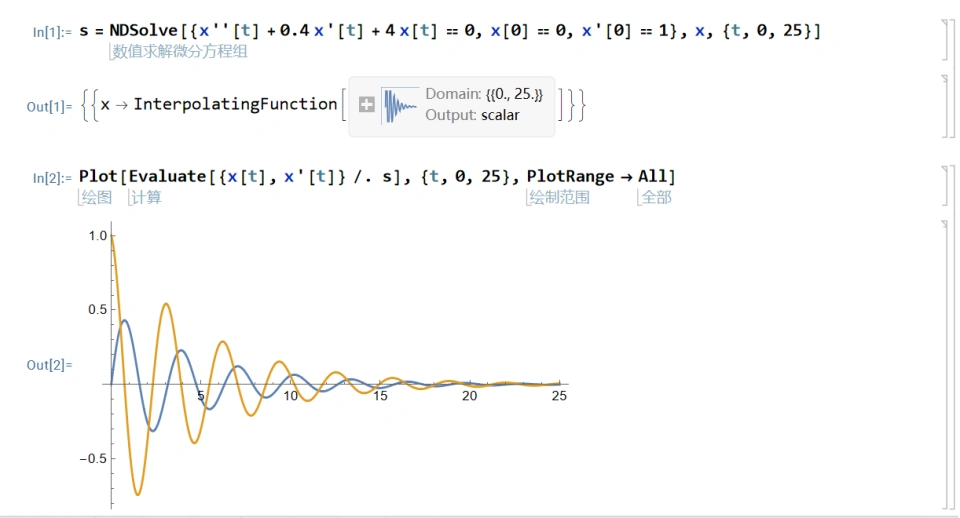
s = NDSolve[{x''[t] + 0.4 x'[t] + 4 x[t] == 0, x[0] == 0, x'[0] == 1},x, {t, 0, 25}]
（1）NDsolve[ { } , x , { } ] 中第一个 { } 里为微分方程的表达式和初始条件即
x''[t] + 0.4 x'[t] + 4 x[t] == 0, x[0] == 0, x'[0] == 1
其中x[t]不能只写成x，不然会报错
（2）NDsolve[ { } , x , { } ] 中 x 表示要求的目标函数为 x
（3）NDsolve[ { } , x , { } ] 第二个 { } 里的内容为目标函数自变量的范围
2.运行以上代码后得到下图所示的结果（结果我也不太懂）
生成了 InterpolatingFunction 的输出，这是一个插值函数（末尾有AI介绍）
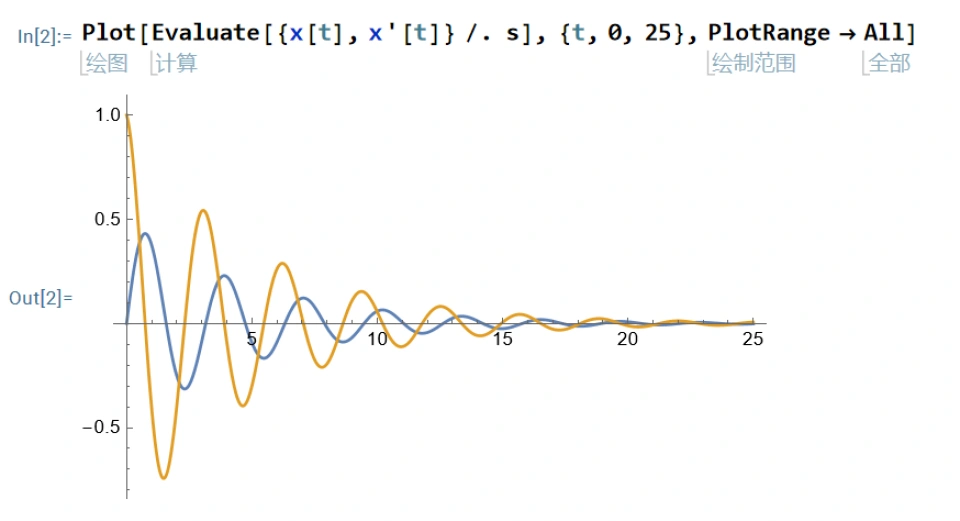
3.然后输入绘图部分的代码运行得到结果
Plot[Evaluate[{x[t], x'[t]} /. s], {t, 0, 25}, PlotRange -> All]
总体界面如下
InterpolatingFunction 通常用于在给定一组数据点的情况下创建一个可通过这些点的平滑曲线。例如，假设我们有一组（x, y）数据点，我们可以通过使用 InterpolatingFunction 来创建一个可以通过这些点的函数，这样我们就可以在任何给定的 x 值下找到对应的 y 值。
请注意，虽然这个 InterpolatingFunction 可以创建出一条平滑的曲线，但并不意味着这条曲线一定完全准确地预测了实际的数据。插值方法的选择以及所提供的数据点的数量都会对插值的结果产生影响。
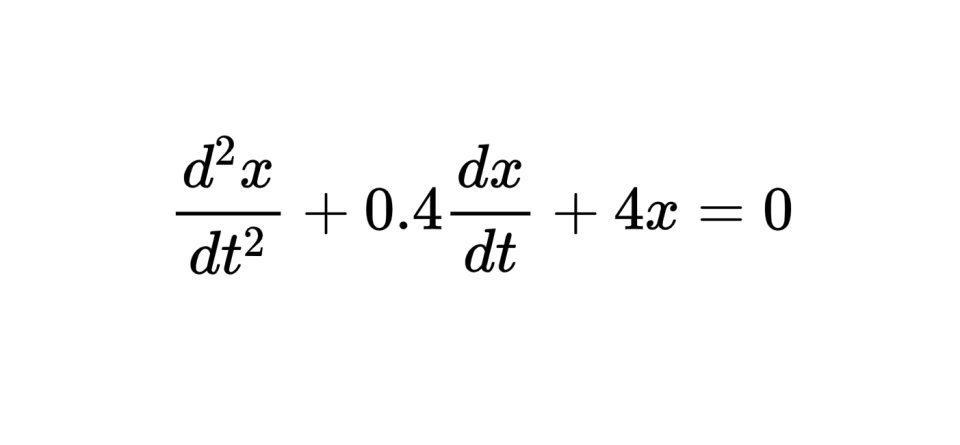
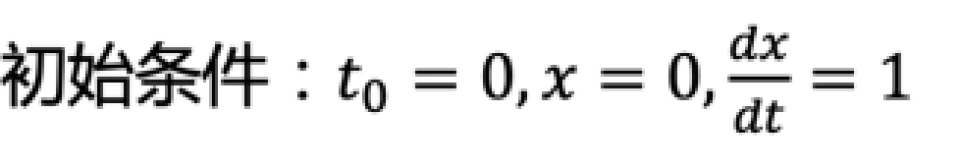
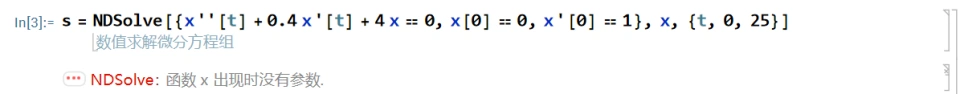
学习了.