博科园AI人工智能助手
图灵
hi 人类
求解的二阶微分方程如下图所示
这是一个阻尼振动的二阶微分方程
β 为阻尼常量
ω_0为振动的固有频率
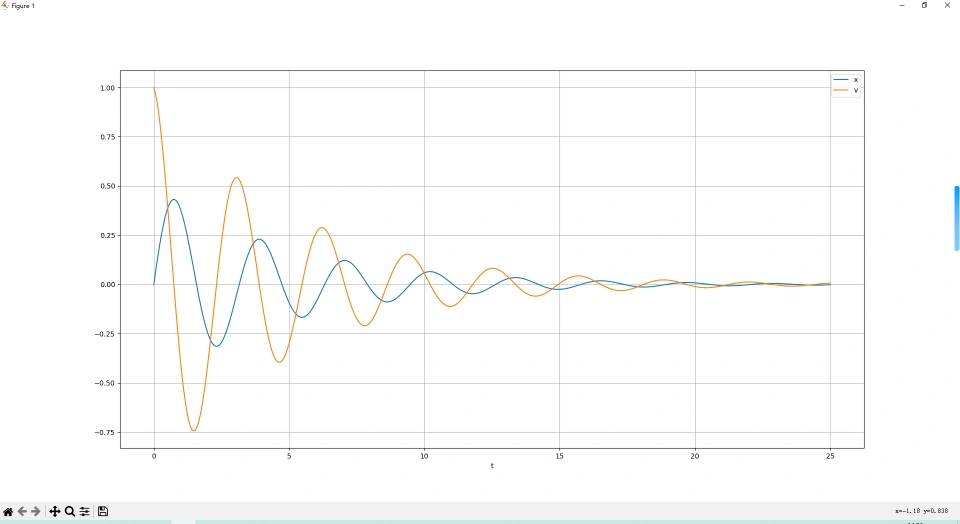
下面通过Python描绘出这个振动的 x-t 和 v-t 的曲线
from scipy.integrate import odeint import numpy as np import matplotlib.pyplot as plt b = 0.2 # b为β 阻尼系数 w = 2.0 # w为ω 固有频率 def pend(y, t, b, w): x, v = y # 求解思路 先对 v'积分得到 v ，再对 v 积分得到 x dydt = [v, -2*b*v-w**2*x] return dydt y0 = [0.0, 1.0] # x=0时， v=1 初始条件 t = np.linspace(0, 25, 1010) # 在[0, 25)里 取1010个 t 的位置 sol = odeint(pend, y0, t, args=(b, w)) # y0为初始条件 应该是对t积分 args=（）传递参数到pend里 plt.plot(t, sol[:, 0], label='x') # sol[:, 0] 获取到解数组 sol 的第一列 即x plt.plot(t, sol[:, 1], label='v') # sol[:, 0] 获取到解数组 sol 的第二列 即y plt.legend(loc='best') # 将标签放在最合适的位置 plt.xlabel('t') plt.grid() # 打开网格线 plt.show()
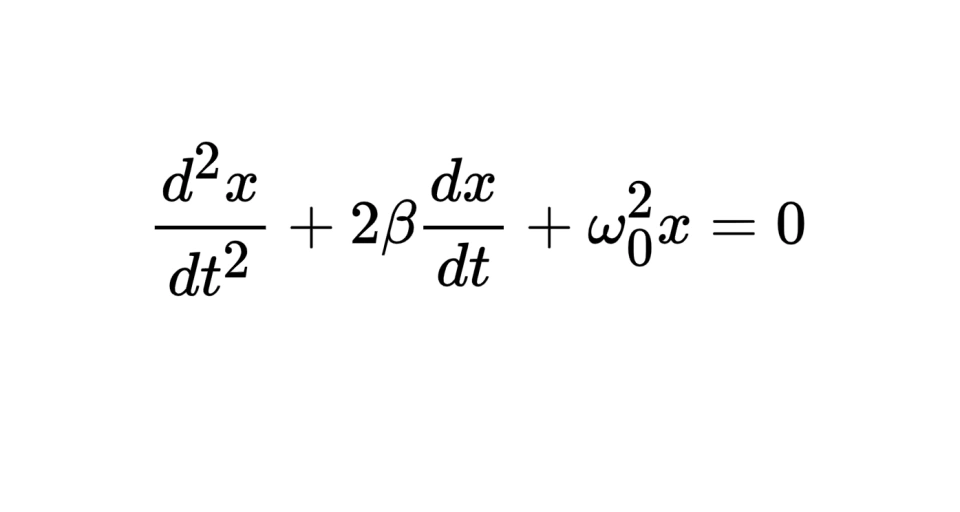
点个赞