博科园AI人工智能助手
图灵
以解 sin^{4}x – cos^{4}x 和 cosx + sinx 为例
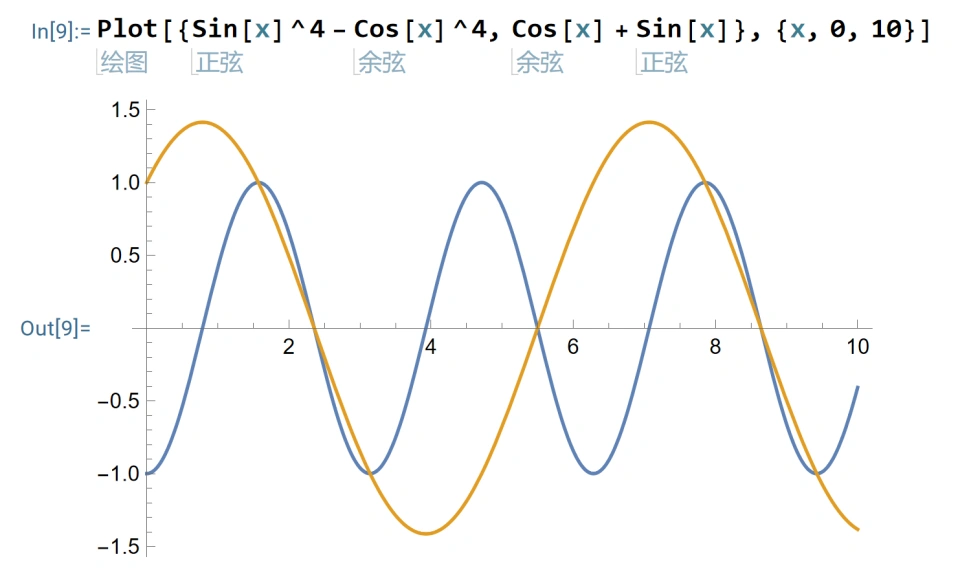
（1）先用Plot方法分别画出 sin^{4}x – cos^{4}x 和 cosx + sinx 的图像，选择适当的横坐标范围展示，这里选择了{x,0,10}
（2）再利用FindRoot方法来准确定位方程的一个根，从图中选取两曲线其中一个交点附近的一个x值，便可得到这个x值附近相对应方程的根，这里取了x在2附近用{x,2}表示
（3）最后得到结果为在2附近方程的一个根为x→2.35619
代码为
Plot[{Sin[x]^4 – Cos[x]^4, Cos[x] + Sin[x]}, {x, 0, 10}]
FindRoot[Sin[x]^4 – Cos[x]^4 == Cos[x] + Sin[x], {x, 2}]
学习了.