在上一篇动态中,我曾提到过一个巨大的数字葛立恒数。相信看过的都大吃一惊了吧?我之前说过,葛立恒数是一个有意义的自然数,但是它大到哪怕是整个宇宙中的所有物质都转换成墨水,也写不下这个数的位数的位数的位数…的位数,只能用高德纳箭头来表示。
再次重申一下:高德纳箭头的定义是这样的:
a↑↑↑…↑n(共有λ个“↑”)表示相对于a将“↑↑↑…↑”(共有λ-1个“↑”)重复n遍。如果是a↑n,则表示a的n次方。
但是,今天我要说到的这个数——TREE(3),它要远远地大于我之前提到的“葛立恒数”,葛立恒数在TREE(3)面前可以算是忽略不计。连高德纳箭头都已经不可用了。
那么,TREE(3)是什么一个数字呢?
首先,我们要明确的是,TREE(x)其实是一个函数,表示用x(x>0且x∈Z)种颜色的点可以画出来的树状图的多少。“TREE”这个单词在英文中的意思就是“树”。那么,我们可以得知:TREE(3)表示用3种颜色的点可以画出来的树状图的多少。
接下来,让我们通过一个小游戏来导出TREE(3)。
在这个树状结构里,我们将小圆点比作树叶,线段比作树干,一棵树不能有闭环,只能从叶到叶,不能从叶到根。从一个叶后面可能引出来若干的叶,这个叶就是成了后面那些叶的根。根和所有的叶组成节点。如此,一棵树上的节点数之和就应该比枝干数之和大1。
另外,小圆点的颜色需要遵循一些规则,而树枝的颜色,我们不用管,因为这和主要问题无关。TREE(3)里的3就代表我们用三种颜色来画这棵树(三种颜色的小圆点)。
画这棵树需要遵循以下两个规则:
1、第一棵树只能有一个节点,第二棵树不能超过两个节点,第三棵树不能超过三个节点……第n棵树最多只能有n个节点。
2、前面的树不能是后面的树的子树;后面的树里,不能“包含”前面的树结构。
需要注意的是,第二条规则里的“包含”是指,后面的树在去掉若干树叶后,依旧不能和前面的树相同(前面的树不能是后面的树的子树,换种方法理解就是,一棵树砍掉任意节点后,不能和前面的树相同。)
除此以外,这种情况也不被允许:当前的树如果取若干节点,这若干节点组成的树结构不能和之前的树的节点产生一一对应的关系。而且,两棵树中任意对应两个节点的最近共同祖先不能是同一颜色。
特别强调:当两个叶子一起朝根节点回溯时,它们一定会在某个叶子上汇合,这个汇合的节点就是他们的最近共同祖先。
理解了上面的规则后,现在画树游戏的要求是:如果两棵树之间,对应节点的共同祖先是同一个颜色,那游戏直接结束。我们要遵守规则,保证游戏一直玩下去。
这种包含关系在数学上的术语叫作:下确界-可嵌入(INF-embeddable),搞硬件嵌入式系统的朋友们应该相当熟悉这个词。这里INF是Infimum and supremum的简称,是下确界或者说是最大下界的拉丁文缩写。
为什么这里要用这个词,因为合适:当我们把一棵树某个枝条上的节点当作一个大小进行排序,且根节点最小时,那么两个节点的最近共同祖先其实就是最大的,且比这两个节点都小的节点。(很绕,但真的就是这样的)
现在我们开始正式画树游戏,我们要画出树尽可能多的森林,也就是“树列”。
从TREE(1)开始,只用一种颜色画树:假设你用的是红色,那么你只能画出一棵树,不然就违反规则了,因此TREE(1)=1。
接下来是TREE(2), 我们用红色和蓝色画树,我们发现,最多只能画出三棵树结构,不然就违反规则了,因此TREE(2)=3。
然后是TREE(3),我们用红、蓝、绿三种颜色,这下神奇的事情发生了,按照这种规则我们可以一直不停地画下去。
那究竟可不可以画完呢?TREE(3)究竟是不是无穷大呢?这就是数学家哈维·弗雷德曼研究的数学问题。结论是:TREE(3)并不是无穷大,而是一个有限的数字,只是比葛立恒数还要大得多。
那TREE(3)不是无穷大这个结论是如何证明出来的呢?如果TREE(3)是无限大,那TREE(3)就没有任何讨论的意义了。就像我们都知道自然数的个数是无限的,讨论最大的自然数没有意义。
TREE(3)这个数是有限的这个结论是经过了严密的证明的,证明人就是计算机领域大名鼎鼎的克鲁斯卡尔。他的证明过程我们可以用一句话总结:如果TREE(3)是无限的,那就一定存在违反规则的情况(一定会存在后面包含前面的情况)。
他的证明方式很巧妙,外行会觉得很不可思议。但是懂行地知道,这是非常厉害且巧妙的一种方法。
那我们如何理解TREE(3)的大小呢?前面我们理解葛立恒数用的是高德纳箭头,但是这种方法在TREE(3)面前根本不管用。面对TREE(3),我们需要用到“超运算表示法”。
我们可以举个例子来理解超运算:
a+b表示a加上b个1的和,用a[1]b表示;
a·b表示b个a相加之和,用a[2]b表示;
a↑b表示b个a相乘之积,用a[3]b表示;
a↑↑b表示b个a组成的指数塔,用a[4]b表示。
举个例子,超4运算:2[4]4=2↑↑4=2↑(2↑(2↑2))=2↑(2↑4)=2↑16=65,536。
了解了超运算之后,这里我们引入a[n]b,超n运算,这里a是底数,b是超指数,n则是阶数。举个例子2[5]4=2↑(2↑(2↑(2(…↑2)↑2))),一共65536个(2[4]4)2。这已经是一个巨型天文数字了。
利用超运算,数学家引入了一个阿克曼函数:A(λ)=2[λ+1]x=2↑↑↑…↑(2[λ]λ)(共有λ-2个“↑”)(其中λ>3且λ∈Z)。另外还要明确一下:An(λ)=A(A(A(…A(λ))))(一共有n个“A”)(n>0且n∈Z)。
上一篇动态中我所说到的葛立恒数,根据数学家的计算,大约为A64(4);而TREE(3)用超运算法,通过阿克曼函数表示就是AA187,196(1)。
今天你惊到了吗?
隐藏内容需要登录才可以看见


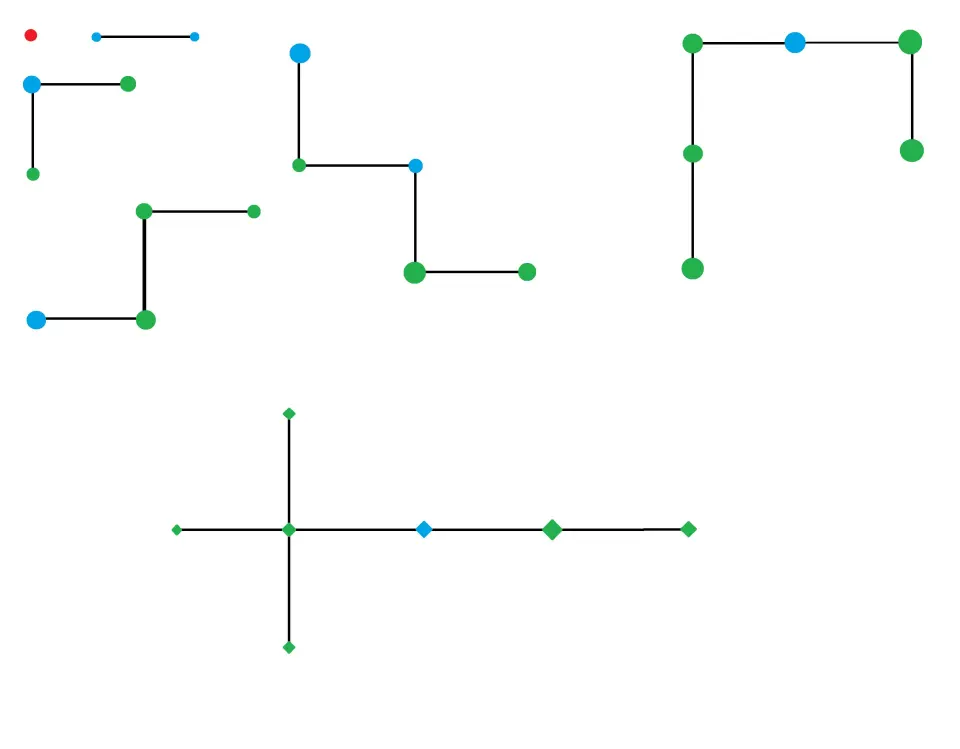













图三表示TREE(3)中可允许的最简单的7种情况。
经典的187196
经典的错误,标准的零分。
这个数字对于TREE3来说小的可以说不存在,是TREE3的一个弱到根本就没有参考意义的下界,用FGH分析,其增长率也不会超过w3。
真正TREE3的增长率在SVO附近,比这篇文章的A(1)^A(187196)大的多的多的多。