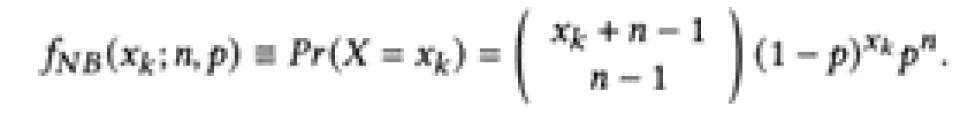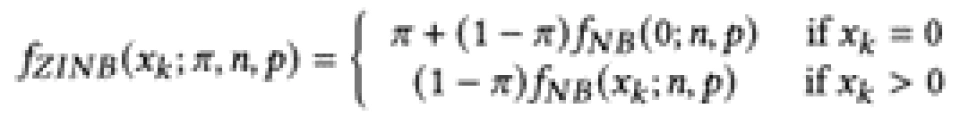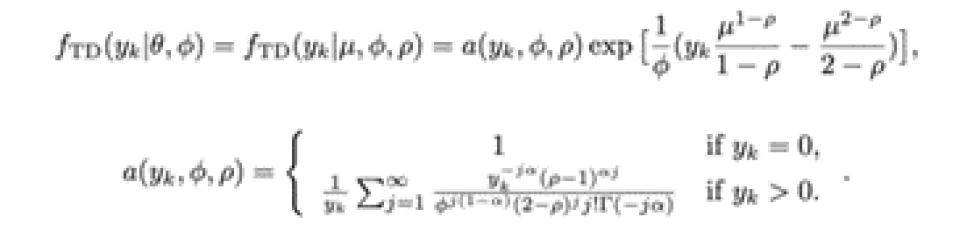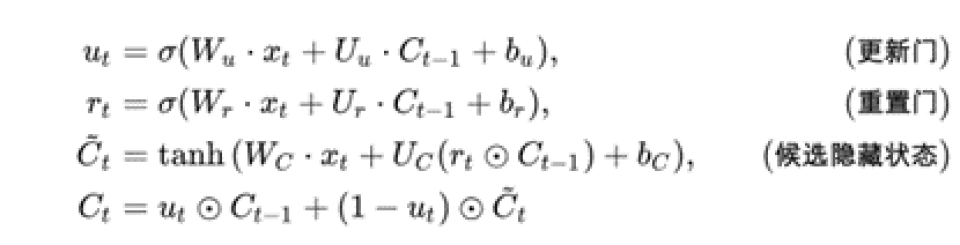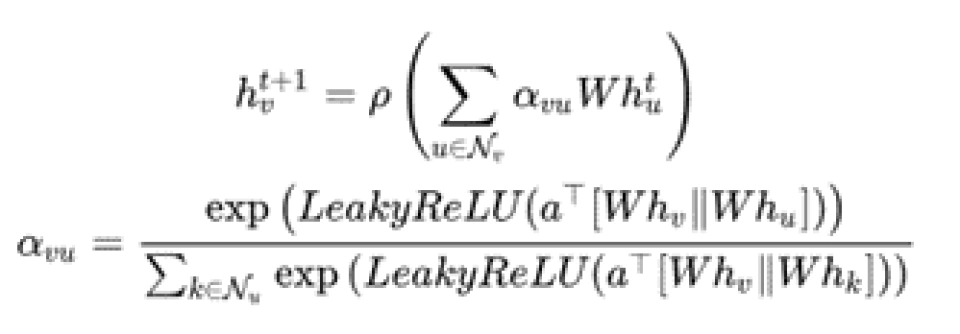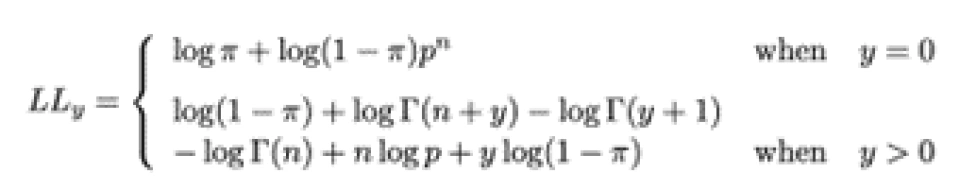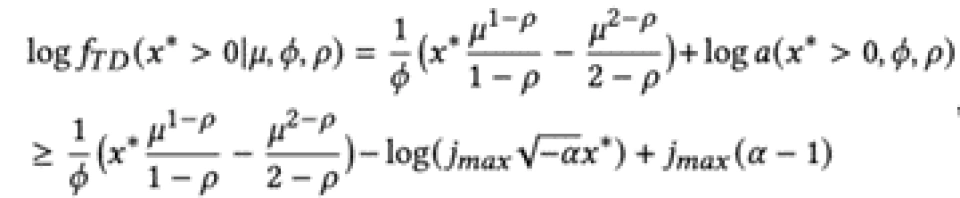作者:张逸仙
审核:时光
一. 介绍
时空数据是复杂而又多样化的数据,分析时空数据能为人类天气预测(如华为盘古大模型)、地质起伏预测、太阳黑子预测、红绿灯优化调度、共享单车投放规划等方面带来重大影响。然而时空数据又是复杂的,体现在其数据的时空变换和空间异质,而其数据分布也极其极端 — 存在大量的零值,以及数据体现长尾分布。
今天要介绍的便是通过引入Tweedie分布和Zero-inflated负二项分布去捕捉零膨胀效应和长尾效应的复杂时空数据,结合时空图神经网络,来衡量预测的不确定性。
1.1 不确定性衡量(Uncertainty Qualification)
想象一下,当我们踏入人工智能这片广袤领域,仿佛迈入一片神秘森林,其中充满了机器智能和前沿科技的奥秘。在这充满活力的领域中,存在一个至关重要的概念,需要我们一同深入探索,那便是不确定性衡量。或许你正在引导一台智能计算机学会识别各种动物,像是让它分辨狗、猫、大象等。但是,当它面对一张全新的动物图片时,需要做的不仅是做出判断,还有告诉我们它对自己的判断有多有信心,这个信心便是–不确定性。
这个过程引发了一个有趣的问题:在计算机模型做出预测时,如何让我们知道它有多确信这个预测是准确的呢? 这涉及到一个核心概念,即模型的不确定性。模型的不确定性涉及它在进行预测时可能出现错误或产生不确定结果的程度。这种不确定性可能来源于两个方面,一个是模型接触到的数据有限,另一个是模型自身的复杂性导致它无法始终做出准确预测。
首先,我们来考虑模型所面临的数据不确定性。就如同当你只看过几张猫和狗的照片后,被要求辨认一种你从未见过的奇特动物一样,模型也可能在面对全新、未曾接触过的数据时感到困惑。毕竟,模型所了解的知识来自于它在训练时接触到的数据,它难以直接将这些知识应用于陌生情境。这就好比你只见过黑色和白色的狗,突然间面对一只蓝色的狗,你也会感到困惑吧?
其次,还有模型本身的不确定性,也就是模型的局限性。设想你要教计算机区分猫和狗,你指示它关注尾巴的长度、耳朵的形状等特征。但是,如果你给它一张模糊的图片,它可能无法精确判断。因为模型并不能像人类一样从模糊的线索中推断出合理结论,它可能因为信息不足而做出错误预测。
为了克服这些不确定性,研究者们提出了一些方法,使我们能更好地理解模型的预测。例如,模型可以输出一个预测的置信度,就好像是它告诉你“我对这个预测很有信心”或者“我对这个预测不太确定”。另一种方法是,模型可以输出一个预测的分布,显示每个可能结果的概率。这种方法类似于掷骰子,你了解每个面的概率,从而更好地预测结果。
通过这些方法,我们可以更清晰地理解模型预测时的不确定性,就像是在未知的森林中多了一张地图,帮助我们更自信地踏出每一步。这一概念在医学、交通、金融等领域都有广泛应用,让我们能更明智地利用模型的预测,做出更可靠的决策。
1.2 时空图神经网络(Spatial-Temporal Graph Neural Network)
时空图神经网络是近年来在深度学习领域异军突起的一项强大工具,为我们理解和处理涉及时空关系的数据开辟了崭新视角。比方说,我们想分析城市中的交通流量变化,或者预测未来气象的演变,这些任务涉及到时间和空间的错综复杂联系。时空图神经网络就如同一把钥匙,为我们敞开了探索时空数据的大门。
首先,我们来解释一下时空数据是什么。时空数据包括了时间和空间信息,比如在不同时间和地点的温度、交通流量、人口分布等。而时空图则是一种用来展示时空数据中关系和相互作用的图结构。在这个图中,节点代表不同的地点或物体,边表示它们之间的关联。
时空图神经网络是专为处理时空图数据而设计的深度学习模型。它结合了图神经网络和时间序列预测的思想,能够帮助我们从复杂的时空数据中提取有价值的信息。这些网络可以捕捉地点之间的关系,同时也能追踪随时间变化的模式,这样我们就能更准确地预测未来、分析趋势,甚至优化决策。
举个例子来说,想象一个城市的交通系统。每个路口可以被视为一个节点,而车辆在不同时刻穿越这些路口则形成了边。时空图神经网络可以学习交通流量在不同路口、不同时间之间的变化规律,这有助于城市规划者更好地优化交通流动,减少拥堵。
这种网络结构在很多领域都有广泛应用。在气象学中,时空图神经网络可以分析全球各地的气象数据,帮助气象学家更精准地预测气候变化。在医疗领域,它可以处理医疗设备产生的时空数据,用于疾病预测和诊断。在金融领域,它可以分析不同市场之间的关系,帮助投资者做出更明智的决策。
1.3 概率模型
在数据分析的舞台上,我们时常会面对一些特殊情况,这些情况使得传统统计方法不再足够。其中两种常见情形分别是长尾数据和零膨胀数据。这些数据背后隐藏着复杂的分布特征,传统统计模型可能难以妥善应对。而此时,概率模型如Zero-inflated负二项分布和Tweedie分布就发挥了关键作用。
长尾数据意味着数据分布中存在着许多数值较小但数量庞大的极端值,这些值往往对模型产生重大影响。比如,分析社交媒体上的点赞数或销售数据中的销售量时,传统的均值和方差等统计量可能无法完全揭示分布的特性。
零膨胀数据则是数据中零值的数量远超预期的情况。举例而言,当我们分析医疗保险索赔数据时,大部分人可能没有提出索赔,导致数据中有大量的零值。然而,传统模型可能因为其假设与实际情况不符而表现不佳。
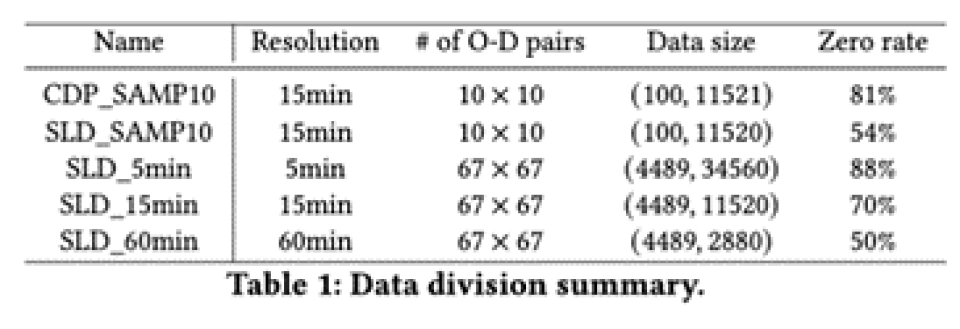
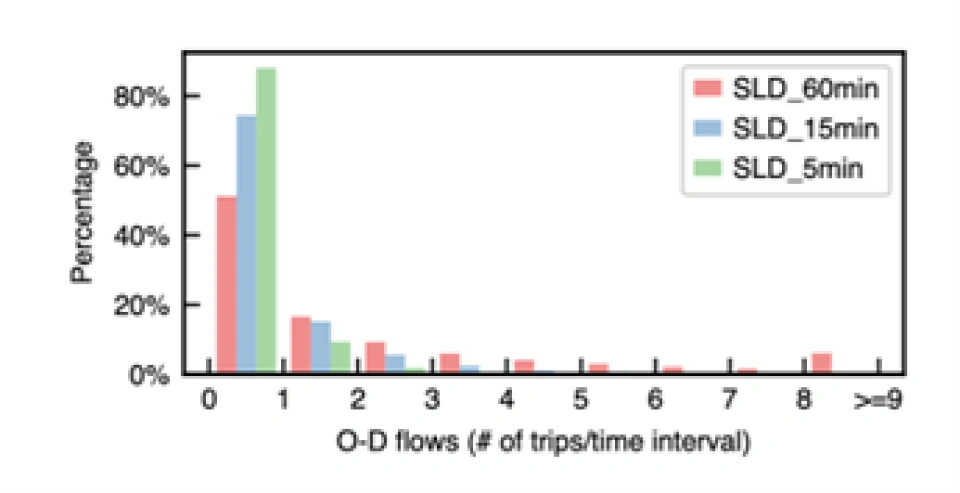
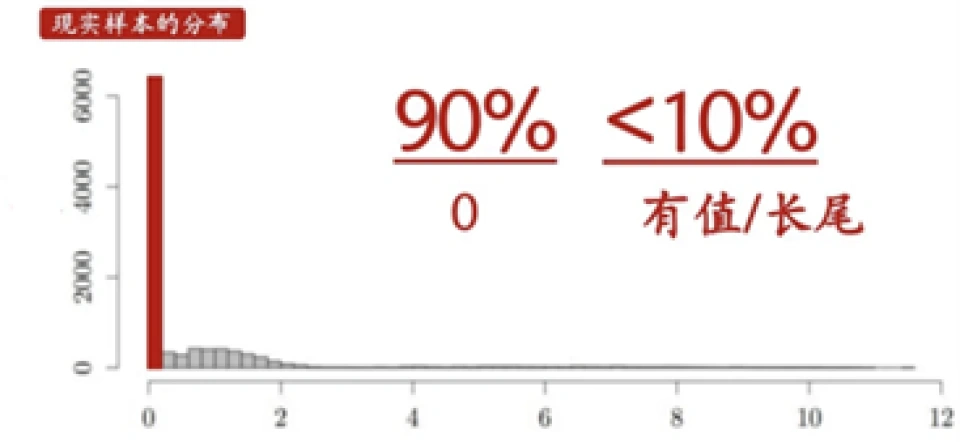
长尾和零膨胀效应在时空数据上体现极为明显,以O-D flows数据(任意两地在任意事件的车流量值)为例:
可以看到在SLD_60min, SLD_15min, SLD_5min这三个数据集上,零值几乎占据了大多数,而大于2的情况所占比例非常少,又明显体现了“长尾”的特点。
为了更好地解决这些问题,Zero-inflated负二项分布和Tweedie分布应运而生。
Zero-inflated负二项分布可以看作是两种分布的结合体:负二项分布(用于计数数据的离散分布)和零膨胀分布(用于描述数据中零值较多的情况)。这种分布适用于数据中不仅存在大量零值,还可能出现较大值的情形。利用这个模型,我们能够更精确地捕捉数据分布的特点,从而更好地进行预测和分析。
Tweedie分布则属于广义线性模型中的概率分布,适用于处理长尾数据和零膨胀数据。其特点之一是广泛适用范围,能够应对连续数据、离散数据、混合数据等多种情况。通过调整Tweedie分布的参数,我们可以更好地拟合实际数据的分布。
这些概率模型在解决长尾数据和零膨胀数据问题上发挥了重要作用。它们不仅有助于更精确地描述和理解特殊类型数据,还为数据分析和预测提供了更强大的工具。医疗、金融、社会科学等领域都广泛应用这些模型,为数据分析带来了更多可能性。
二. 算法介绍
今天要介绍的是发表在数据挖掘顶会(SIGKDD [1]和CIKM [2] )和地理学顶会(GIScience [3])的三篇论文:作者是麻省理工大学Dingyi Zhuang,伦敦大学学院的Xiaowei Gao和北京大学的Xinke Jiang。
[1] Uncertainty Quantification of Sparse Travel Demand Prediction with Spatial-Temporal Graph Neural Networks. SIGKDD 2022.
[2] Uncertainty Quantification via Spatial-Temporal Tweedie Model for Zero-inflated and Long-tail Travel Demand Prediction. CIKM 2023.
[3] Uncertainty Quantification in the Road-level Traffic Risk Prediction by Spatial-Temporal Zero-Inflated Negative Binomial Graph Neural Network(STZINB-GNN). GIScience 2023.
2.1 分布介绍
2.1.1 负二项分布(Negative Binomial Distribution)
负二项分布是统计学上一种离散概率分布,用于描述在重复试验中获得固定数量的成功所需的独立失败次数的分布。这个分布经常用来描述不定次数的成功事件,例如在多次投掷硬币直到获得一定数量的正面朝上为止。
与二项分布不同,二项分布描述的是进行固定次数试验中成功次数的分布,而负二项分布则关注在获得固定数量成功之前所需的试验次数。负二项分布在许多实际场景中都有应用,比如在金融中用于分析投资成功前的失败次数,或者在生物学中用于研究实验成功前需要多少次不成功的尝试。这个分布提供了一种数学工具,帮助我们理解和解释各种随机事件中的概率分布。
满足以下条件的称为负二项分布:实验包含一系列独立的实验,每个实验都有成功、失败两种结果,成功的概率是恒定的,实验持续到n次不成功,n为正整数。切换到我们的时空数据中,成功即数据非0,失败即数据为0。
其概率分布如下:
这里的 n 和 p 是模型参数,分别表示成功的次数和单次失败的概率。
2.1.2 零膨胀负二项分布(Zero-Inflated Negative Binomial Distribution)
然而,现实世界中的数据通常会出现许多零观测值。零值的激增加剧了负二项分布参数的学习。因此,引入了一个新的参数 pi 来学习零值膨胀率,从而得到了零膨胀负二项分布。
零膨胀负二项分布(Zero-Inflated Negative Binomial Distribution,简称ZINB分布)是一种概率统计学中的概率分布,用于处理数据中存在大量零值的情况,同时考虑了负二项分布的特性。
在现实世界的数据中,往往会有很多零值的存在,这可能是因为某些特定原因导致的。例如,在社交媒体上的点赞数量中,很多帖子可能没有被点赞,导致数据中存在许多零值。然而,传统的负二项分布在处理这种情况时可能表现不佳,因为它无法很好地捕捉到数据中的零值特征。
ZINB分布的引入就是为了更好地处理这种零值问题。它结合了两个部分:一个用于描述零值的部分,另一个用于描述非零值的部分。具体而言,ZINB分布中引入了一个额外的参数 pi,用于表示数据中零值的膨胀程度。在生成数据时,有 pi 的概率产生零值,而有 1 – pi 的概率遵循负二项分布生成非零值。这样,ZINB分布能够更准确地刻画存在零值的数据特征,并在建模和分析过程中更加适用。
其概率分布如下:
在负二项分布的基础上,考虑了零值的加权。这里的pi即为零膨胀系数。
ZINB分布在许多领域的数据分析中都有应用,特别是在处理存在大量零值的数据集时,如社交媒体数据、医疗数据等。通过引入零膨胀参数,ZINB分布帮助我们更好地理解和解释这些特殊类型的数据,并提供了更准确的分析工具。
2.1.3 Tweedie分布
负二项分布是对零值做了一定的处理,但不能适用于极度零值的情况;因此通过引入新参数pi来对零值做加权,加强了模型鲁棒性。然而,有过多零值的出现,就一定会有长尾效应的产生,因此如何建模长尾效应也是一个值的考虑的问题–Tweedie分布。
Tweedie分布示意图
Tweedie分布是一种概率统计学中的广义线性模型,用于建模和分析具有复杂分布特征的正数数据。这种分布在描述连续、离散和混合数据等多种数据类型时都具有应用价值。Tweedie分布由一系列的特殊情况组成,包括正态分布、伽马分布、泊松分布等。它的灵活性使得它能够适应各种数据分布的特点,而不需要对每种特定情况进行单独的建模。Tweedie分布的参数化形式取决于两个主要参数:指数参数和离散参数。指数参数决定了数据的分布形状,离散参数则控制了数据的离散程度。通过适当地选择这些参数,可以使Tweedie分布拟合多种数据类型,包括长尾数据和零膨胀数据。
Tweedie分布的概率密度函数如下:
这里一共有三个参数:离散系数phi, 指数系数rho和模型均值mu。
在实际应用中,Tweedie分布广泛用于处理存在多样性和复杂性的数据集,如保险索赔数据、金融时间序列数据、生态学数据等。通过使用Tweedie分布,我们能够更好地捕捉和解释数据的分布特征,从而进行更精确的分析、建模和预测。
综上所述,为了更好的建模时空图的某一个时间点的某一个地理点的数据以及其不确定性,我们采用二参数模型(NB),三参数模型(ZINB和Tweedie)来计算模型的不确定性。
2.2 时空图神经网络介绍
如何建模每个分布的参数成为了一个棘手的问题,但在时空数据上,我们可以采用时空图神经网络来建模。
而为了学习这些参数,我们使用了时空图神经网络(STGNN)– 这个神经网络的设计有点像是在解谜,它通过一个时间编码器和一个空间编码器来学习参数的值。
具体而言:时间编码器使用了一种叫做门控循环单元(GRU)的技术,类似于人类大脑中的一些运作方式,来处理数据中的时间信息。
GRU计算公式
而空间编码器则使用了图注意力网络(GAT),就好像在数据之间建立了一种连接关系,帮助我们更好地理解数据之间的关联性。
GAT计算公式
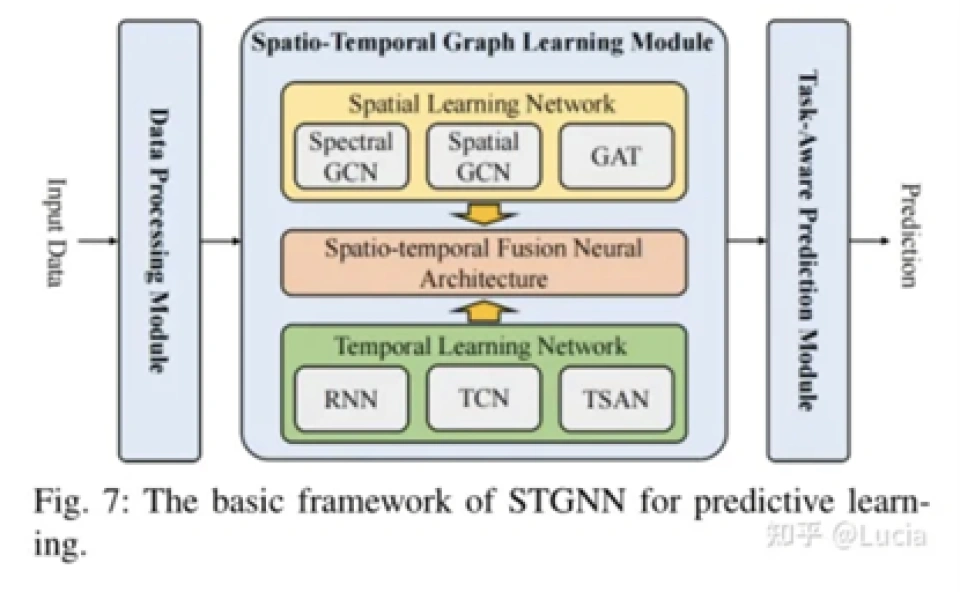
其STGNN网络框架如下:
(图来自知乎用户:Lucia)
通过这个特殊的时空图神经网络,我们能够更准确地学习数据模型中的参数(二参数、三参数等),基于该参数构建结果分布,从而更好地分析数据,做出更可靠的预测。这就像是在解谜一样,不断优化网络,让我们的数据分析变得更加精准和有用。
2.3 模型训练指导函数
作者采用最大似然函数方法来指导模型训练。
最大化似然函数是一种在统计学和概率论中常用的方法,用于找到最适合数据的参数值,以便使得数据出现的概率最大化。
让我们用一个简单的例子来解释这个概念。假设你有一堆骰子掷出的数据,你想要找出这个骰子是均匀的还是有偏的。你知道这个骰子有6个面,但你不知道每个面出现的概率。你可以用一个参数p来表示每个面出现的概率,然后构建一个概率模型。
现在,你有了一些实际掷骰子得到的数据,比如说你投了100次骰子,记录下每次的结果。你的目标是找到一个参数p,使得在这个参数下,投出这100次骰子的概率最大化。
这就是最大化似然函数的思想。似然函数表示的是,在给定参数的情况下,观察到实际数据的概率。你要做的就是调整参数,使得这个概率最大化,也就是让观察到的数据在模型下出现的概率最大化。
最大化似然函数是一种寻找最优参数的方法,它在许多领域都有应用,从机器学习到统计分析。通过找到最适合数据的参数,我们能够更好地理解数据的规律,从而做出更准确的预测和决策。这个方法就像是在拼图,我们不断尝试不同的拼法,以找到最符合实际情况的模型。
2.3.1 ZINB最大似然函数
其中pi, n, p均为通过STGNN学习所得,不断得优化该函数,能达到模型的训练目的。
2.3.2 Tweedie最大似然函数
其中rho, phi, mu均为通过STGNN学习所得,不断得优化该函数,能达到模型的训练目的。