2009年,知名科幻电影《阿凡达》上映,许多观众从来没有见过这样的作品——无垠的森林,漂浮的山脉,雄伟的生物共同组成了潘多拉星球美丽的景色。这部电影在当时备受好评。
《阿凡达》中所说的潘多拉星球,是这部电影中虚构的位于半人马座α(南门二)附近的气态巨行星“波吕菲密斯”的其中一颗卫星。那里也是纳威人赖以生存的家园。
现在,闲话不多说,直接转入正题。
1、参宿四
参宿四,即猎户座α(Alpha Orionis),其天文学特有名称是Betelgeuse,是一颗光谱为M1-2(M1-M2Ia-ab)型的红超巨星,位于猎户座内。它的半径大约是太阳的887到955倍,是不用双筒望远镜也能看到的最大恒星之一。其视星等在0.0到1.3之间变化,通常是猎户座的第二亮星,也是全天第十亮的恒星。
大多数时候,参宿四只比波江座的水委一稍暗一点,比半人马座的马腹一稍亮一些。在红外波段上看,参宿四比天空中的其他恒星都要亮。尽管它只有800万到850万年的年龄,但它是一颗演化迅速的大质量恒星,已经接近其生命周期的终点。在不久的将来,这颗恒星将会变成一颗超新星,到那时,它将释放出形成新一代恒星所需的物质。
2、参宿四与南门二之间的距离是多少
由天文通App的数据可知,参宿四的赤道坐标是(05h56m25.3s,+07°24′40.6″),距离地球427.50光年;南门二的赤道坐标为(14h41m23.1s,-60°55′44.2″),距离地球4.42光年。将参宿四与南门二的赤道坐标转换成纯度数,则参宿四为(89.11°,+07.41°),南门二为(220.35°,-60.93°)。
接下来就是确定参宿四与南门二之间的距离是多少。
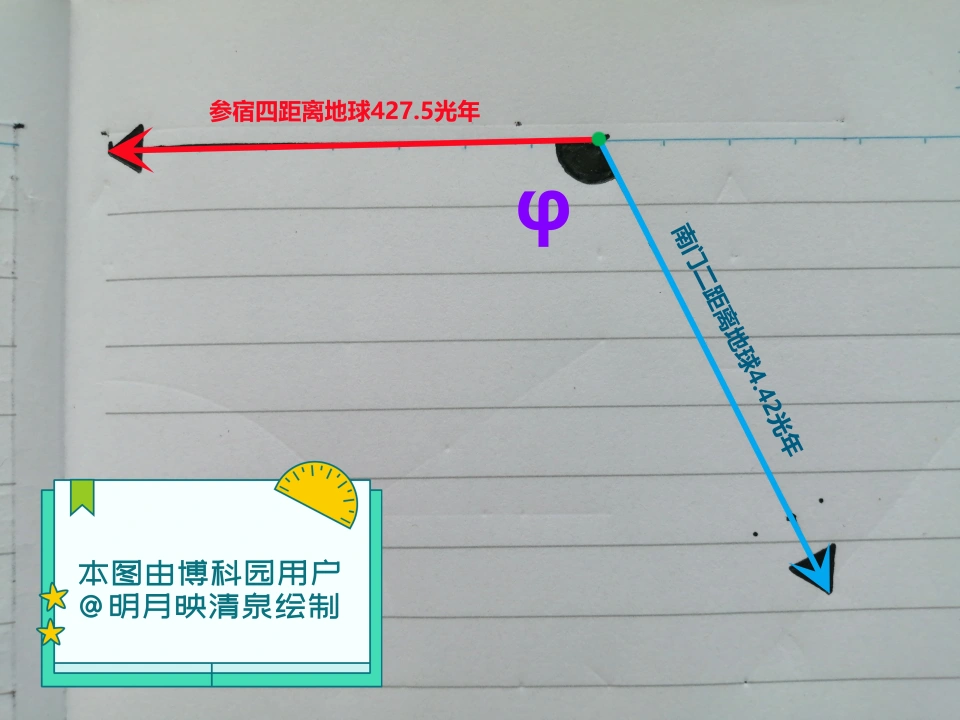
令球面上的两点A、B的赤道坐标分别为(α1,δ1)、(α2,δ2)。那么,通过向量的运算法则,我们可以知道,令∠AOB=φ,则cosφ=(cos(δ1)•cos(δ2))•(cos(α1)•cos(α2)+sin(α1)•sin(α2))+sin(δ1)•sin(δ2)。将之前所得的数据代入cosφ的表达式中,可得cosφ=-0.43(φ=115.5°)。
再利用余弦定理,令地球与参宿四的距离为a,与南门二的距离为b,参宿四与南门二之间的距离为c,
那么由c↑2=a↑2+b↑2-2a•b•cosC,可得c=429.42光年。这与a的数值没有多大差别。也就是说,纳威人如果看到了参宿四的超新星爆发,那么其亮度与地球上看到的没有多大差别。
隐藏内容需要登录才可以看见



![[s-60]](https://www.bokeyuan.net/pic/image/emoji/cas/60.png)












