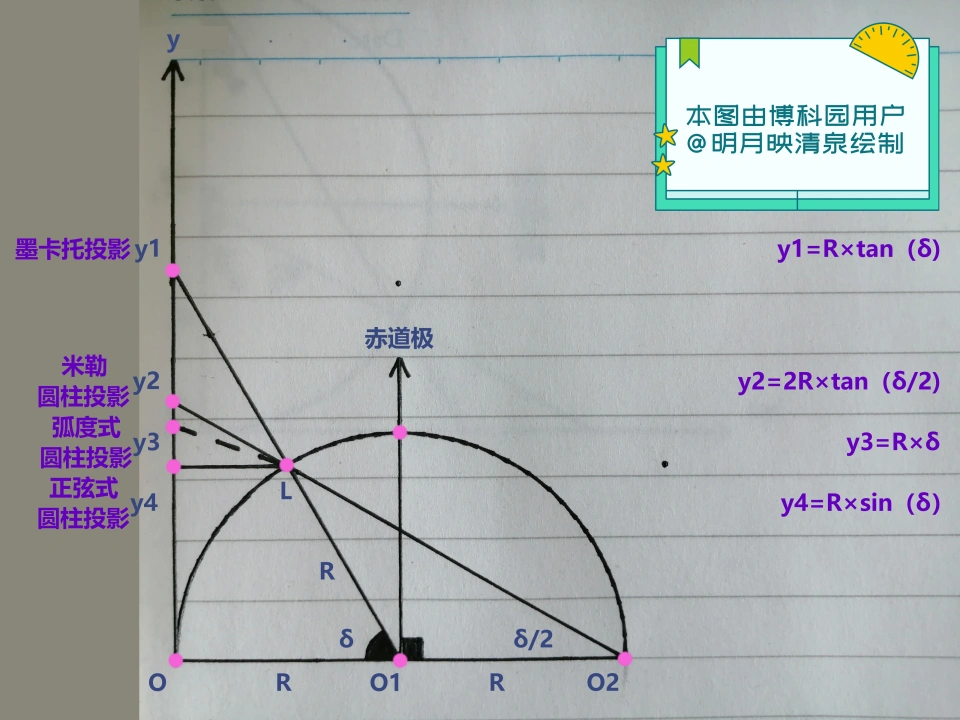
所谓的“圆柱投影”，实际上是地图投影模式的一大类，指得是通过一定的数学方法，将球面投射到圆柱面的投影模式。
设被投影的球体的半径为R，如果圆柱面与被投影的球体在赤道圈相切，那么由圆的周长公式可得，圆柱面展开之后所得的平面图，其横长L=2πR。
1、墨卡托投影
墨卡托投影，也叫正轴等角圆柱投影。由荷兰地图学家墨卡托(G.Mercator)于1569年创立。该投影模式所基于的数学原理是：将一个与地轴方向一致的圆柱面与地球赤道相切，按照等角条件，将经纬网格投射到圆柱面上，然后再将圆柱面展平，即得本投影。该投影模式也是最早且最常用的圆柱投影。
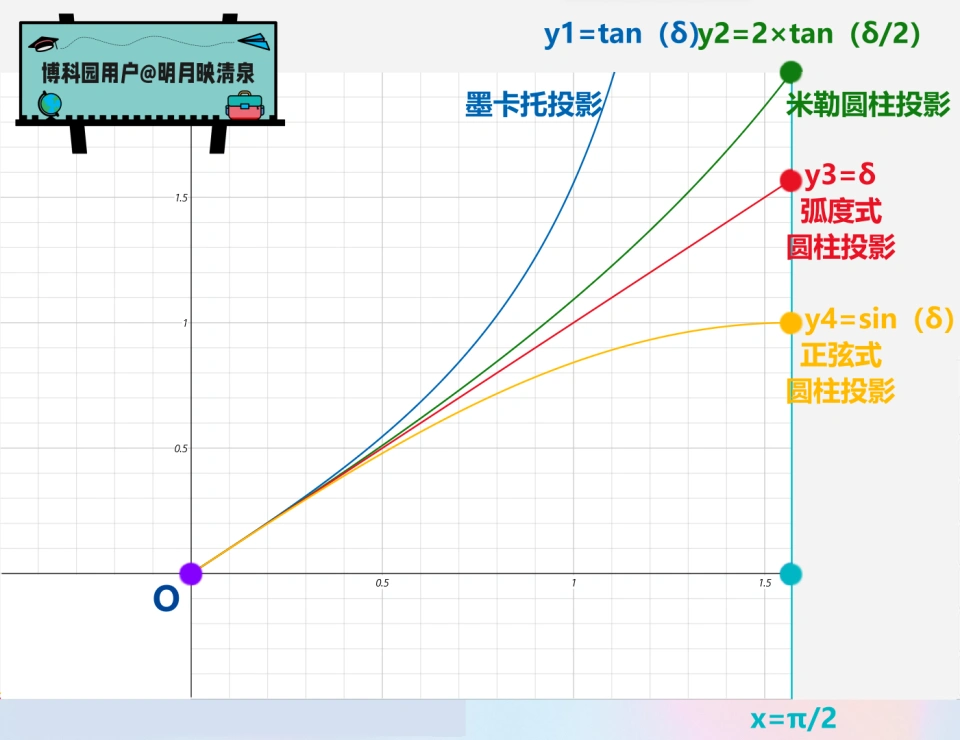
该投影模式需要用到的公式为y=R•tan(δ)，其中，δ代表纬度，y代表δ纬度线在地图上与赤道线的距离。
但是，该投影存在一个缺陷：由于f(δ)=tan(δ)不能对δ±90°进行定义，致使墨卡托投影不能绘制完整图幅。现在大家应该知道我之前的动态中没有哪一张实时星图采用墨卡托投影的原因了吧？
另外，令黄赤夹角为δ0，那么通过数学推导可得，黄道线上的任意一点的赤道纬度δ与赤道经度α、黄赤夹角δ0之间的数学关系tan(δ)=sin(α)•tan(δ0)，也就是说，如果将黄道线投射到墨卡托地图上，那么它的形状就是一条标准的正弦曲线。
2、米勒圆柱投影
米勒圆柱投影，是一种修正过的墨卡托投影，在1492年由Maitland Miller (1897-1979)提出，它可以对δ±90°进行定义。
该投影模式可能需要用到的公式为y=2R•tan(δ/2)。
另外，通过数学分析，可得当δ→0时，(tan(δ))/(2tan(δ/2))→1。因此，在赤道附近，墨卡托投影与米勒圆柱投影非常接近。因此米勒圆柱投影，是一种修正过的墨卡托投影。
3、弧度式圆柱投影
弧度式圆柱投影，也叫等距圆柱投影，在该投影模式的地图上，所有经纬线的投影都是相同间距的。所需要用到的数学公式为y=R•δ。
4、正弦式圆柱投影
熟悉单位圆的读者应该都能理解，该投影模式所需要用到的数学公式为y=R•sin(δ)。
附图：圆柱投影的几何原理。
