高一暑假某天,我坐在帐篷里,看着草地上来回奔跑的小朋友,手上拉着风筝线放风筝,随着风筝越飞越高,我不禁好奇:放风筝时,风筝线是什么形状的?
不过那时的我还不具备足够的知识来解决这样的问题,于是我打开知乎,向万能的知友求助 。没过多久,一个个神奇的回答为我打开了新世界的大门 !
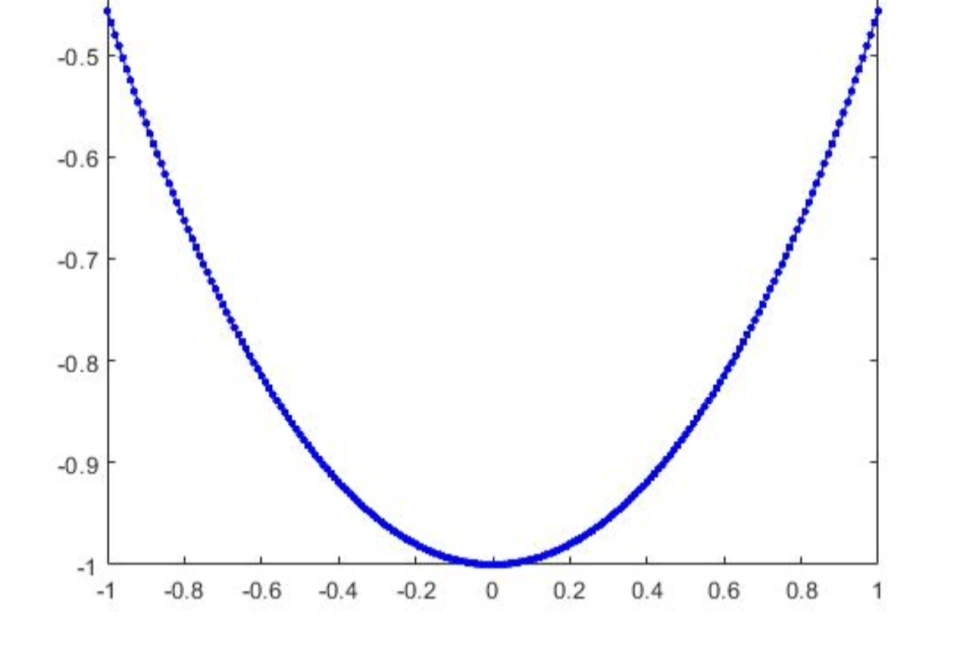
答案是:在理想情况下,它是一条悬链线(Catenary)
怎么来的呢?
首先,我们简化模型。假设风筝稳稳地飘在天上,而在地上的我们用水平恒定的拉力扯着风筝线。咱们暂时先不考虑线的厚度和风的荷载对线形的影响。
其次,建立坐标系,设我们手的高度为h,给线的水平拉力为H,风筝给线的拉力为T,且T与水平面呈θ的角度,线的密度处处均匀为ρ。
最后,建立平衡方程,得到一条ODE,然后瞪眼可得悬链线方程。
那么问题到此就结束了吗?如结。到底结没结束?如结。
这时我看到另一篇回答,这篇回答介绍了物理学中一个很重要的、很妙的原理——最小作用量原理(Least Action Principle)。这时,你还可以这么问:为什么它正好就是悬链线呢?为何不是抛物线或其他曲线呢?
不同于牛爷爷的做法,与其去一个个分析系统的受力情况,我们不如对整个系统的势能函数进行研究。一通计算猛如虎,我们同样也能给出悬链线方程。
可以这么想,风筝线为了让其自身处于其势能最低的状态它把自己变成了悬链线。
(正如我每天吃饱喝足了就想躺下,而不是起身去工作 )
某种意义上,这个原理揭示了宇宙万法的那个源头其实是——懒!(bushi)
最小作用量原理
是从物理学中许多和一个系统内与“作用”有关的概念,例如:力的作用,能量的作用,电的作用等抽象出来统一描述为“作用量”,并给出自然界所有作用量都趋向于最小值的这样一个“世界观”。宁就说妙不妙吧。是不是感觉这个原理揭示了一种化繁为简“做减法”的生活至理。
好,那么问题到此就结束了吗?如结。到底结没结束?如结。
在一篇回答里,我看到了这样一句话:现实世界水很深。
(难怪我的生命一直在下沉
却又对这世界爱的深沉bushi)
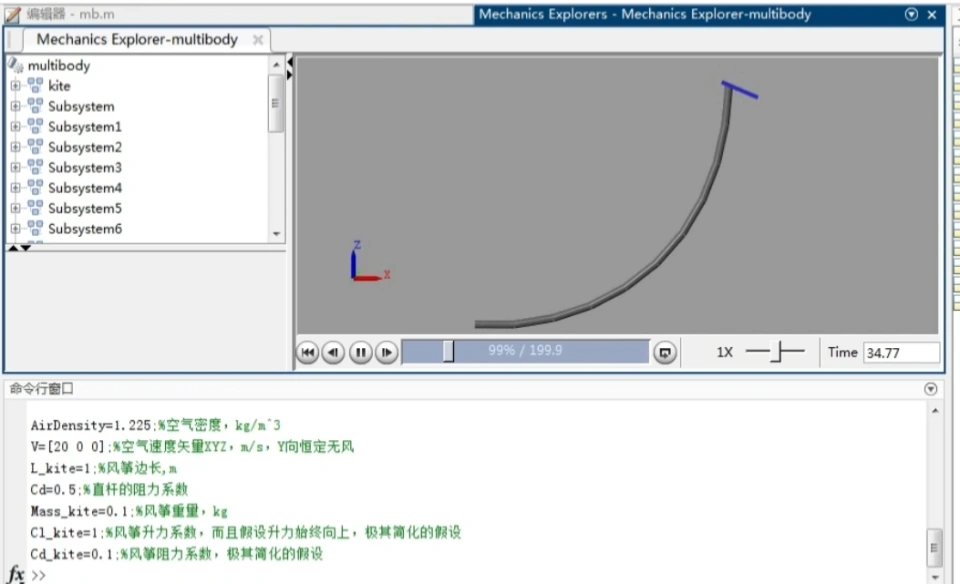
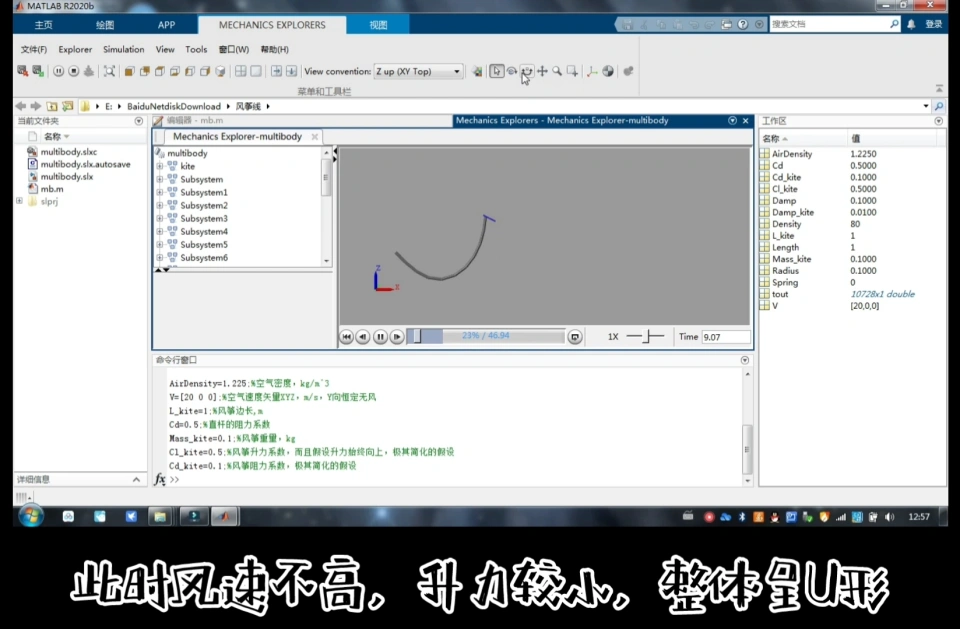
那就让我们打开Matlab,看看模拟出来的结果是怎样的。
(该Matlab模拟文件可在公众号“飞行课”里回复“风筝线”获取)
到此,我们对放风筝时风筝线的形状有了一定的了解。让我们再回来看看它的理想线形——悬链线。既然有悬链线,我又开始好奇:那是不是还有悬链面呢?
让我们把悬链线绕x轴旋转一周,那么所得到的旋转曲面就叫悬链面,通过查资料,可以知道它是唯一的旋转极小曲面。至于这“极小曲面”术语是啥,以后有机会的话再跟大伙儿说说,现在的问题是:现实生活中存在这样一个曲面吗?请看下面这个实验。
为何这泡泡膜是这样的形状呢?我们同样的也可以利用最小作用量原理来解释。
综上,一个简单的问题,不管答案是简单的还是复杂的,寻找这个答案的过程却是多样而奇妙的。生活正是这样,它不会告诉你答案,它要让你自己去寻找,去经历。或许你穷尽一生也无法找到答案,但请感激,生活给了你不止一条让你接近答案的路。


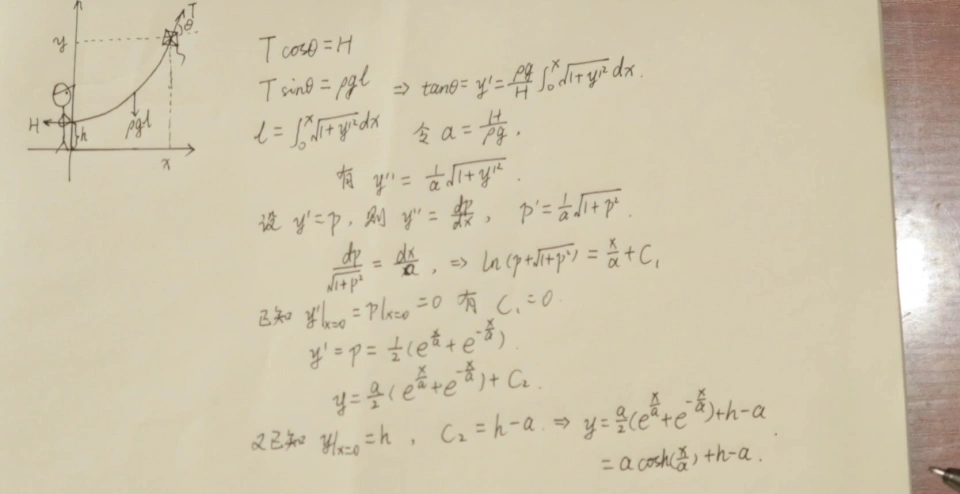



![[s-14]](https://www.bokeyuan.net/pic/image/emoji/cas/14.png)
![[s-70]](https://www.bokeyuan.net/pic/image/emoji/cas/70.png)
![[s-60]](https://www.bokeyuan.net/pic/image/emoji/cas/60.png)












