引言:给我最大欢乐的,不是已懂得知识,而是不断的学习;不是已有的东西,而是不断的获取;不是已到达的高度,而是继续不断的攀登。——高斯
朋友们好!好久没有发博科园了,在匆忙的生活中,耽误了很久。不过幸好最近有点时间,抽空给大家写篇文章。其实关于群论的内容我之前就一直想写,毕竟我花费了很多心思,而且还有很多感想。其次就是我这次不是只写一篇文章,这将是我的一个专题,是一个系列,相信大家凭着标题也看到了,这篇文章只整个系列的开头。而我为什么选择群论这个专题来写呢?
首先,我之前写过图论的一点内容,图论和群论关系又很大;然后群论本身内容也算代数基础,我不会写得很深,结尾大概会是伽罗瓦理论,初中生可以勉强看懂,高中生也可以学会,我强调其中的思维,尤其是里面的抽象思维,不管在哪个领域都很适合。还有一点,就是我要通过这个系列把数学的很多领域窜起来,可能还会有其他学科客串,也是希望大家多多期待与帮助了。
我也不说那么多,下面就正式进入正题。
一、命题与逻辑
现在,我们进入数理逻辑的学习。
数理逻辑是研究推理的数学分支。你可会有点突然:”推理是什么?”面对这个问题,我们先看几个句子:
①2是素数.
②雪是黑色的.
③2+3=5.
④明天是晴天.
⑤请关上门!
⑥x>2.
⑦什么是推理?
⑧这朵花真好看!
以上几个句子,显然⑧是感叹句,⑦是疑问句,⑤是祈使句,而其余的都是陈述句,看完这些句子,现在我们先引入命题的基本概念:
命题是可判断某一件事情真假的陈述句.
所以,命题是一个陈述句,而且它的判断结果只有两个值:真或假。当一个命题判断为真时,叫做真命题。当一个命题判断为假时,叫做假命题。
上述九个句子中,我们可以判断出⑤⑦⑧非命题,⑥无法判断真假,所以也不是命题,①③为真命题,②为假命题,④和⑨我们还不确定是真是假,但是我们知道,④和⑨真假唯一,且随着时间推移,我们可以判断出真假性,所以④和⑨依然为命题。
现在,我们可以给出推理的定义:
推理是指从前提出发推出结论的思维过程.
这里,前提是已知的命题,结论是从前提出发应用前提出发应用推理规则推出的命题。一般在命题判断过程中,我们默认推理的过程正确。
考察命题“若p,则q”。一般地,“若p,则q”为真命题是指由p通过推理可以得出结论q,并且这一过程可以可以表述为:
p⇒q,
其意思可以简化为,p可以推出q,并且说,p是q的充分条件,q是p的必要条件。如果“若p,则q”是假命题,那么由前提条件p推不出结论q,即p不是q的充分条件,q不是p的必要条件。因为推理的过程默认没问题,所以如果p是q的充分条件可以理解为:p成立q一定成立。(即p可以推出q,但并不代表p不成立q就不成立)。同样的,q是p的必要条件可以理解为:q不成立p就不成立(因为p能推出q,但q却是不成立的,则p也是不成立的)。
在进入集合概念学习时先给出几个概念:
1° 所有的命题都有条件和结论
2° 当命题条件和结论都为命题时,该命题一定含有推理过程。
3°如果一个命题的条件和结论分别是另外一个命题的结论和条件,那么这两个命题叫做互逆命题,其中一个命题叫做原命题,另外一个命题叫做原命题的逆命题。
4°若其中一个命题的条件和结论分别是另一个命题的条件的否定和结论的否定,则这两个命题互为否命题。如果把其中一个称为原命题,那么另一个就叫做它的否命题。简称”非p“符号,表述为 ┐p。
5° 如果“若p,则q”和它的逆命题“若q,则p”均是真命题,即p⇒q,q⇒p,记作:
p⇔q,
此时p既是q的充分条件也是q的必要条件,我们称p是q的充分必要条件,简称充要条件。
6°在命题的条件中,我们通常要用指定范围内的全体对象或该指定范围整体的含义的词,例如:任意正方形都是平行四边形、存在实数x,x>3,其中的“任意”“存在”我们也可视为条件的一部分,前者称为全称量词,用符号”∀”表示,后者称为存在量词,用符号”∃”表示。
通常,将含有变量x的语句用p(x),q(x),r(x)……表示。
二、集合与数学归纳法
集合是不能精确定义的数学概念。直观地,一些事物汇集到一起组成的一个整体就称作集合,而这些事物就是这个集合的元素。
集合通常用大写的英文字母标记,如自然数集N(我们在这里不把0做自然数),实数集R,整数集Z,有理数集Q,复数集C等。
如果a是A中的元素,就说a属于A,记作a∈A;如果a不是A中的元素,就说a不属于A,记作a∉A。
表示一个集合的方法有两种:列举法和描述法。
列举法 一一列出集合中的所有元素,元素之间用逗号隔开,并把它们用花括号”{ }“括起来。
例如A={1,2,3},B={a,b,c,…,z)
描述法 一般地,设A是一个集合,我们把集合A中所有具有共同特征P(x)的元素x所组成的集合表示为{x∈A|P(x)}
例如{x|x>2},默认表示x属于实数集R,大于2的实数组成的集合,当然,我们已说明,x不一定是数,如{x|x是平行四边形}。具体是什么,还得按情况而定。不过特殊的集合会告诉你,如{x∈Z|x>2}。
对于任意一个元素,要么它属于某个指定集合,要么它不属于该集合
集合的元素具有互异性,即元素是互不相同的,{1,2,2,3}={1,2,3}
集合的元素具有无序性,即{1,2,3}={1,3,2}
定义 1.1 设A,B为集合,如果A中的元素都是B中的元素,则称A为B的子集。这时称A包含于B,(或B包含A),记作
A⊆B(或B⊇A)
定义 1.2 设A,B为集合,如果A⊆B且B⊆A,则称A与B相等,记作A=B。
定义 1.3 设A,B为集合,如果A⊆B且A≠B,则称A是B的真子集,记作A⊂B。
定义 1.4 不含任何元素的集合称作空集,记作Ø。
定理 1.1 空集是一切集合的子集。(这很显然)
推论 空集是唯一的
证 若∃Ø₁,Ø₂,则有Ø₁⊆Ø₂,Ø₂⊆Ø₁(定理1.1)根据定义1.2可知Ø₁=Ø₂.
Q.E.D.
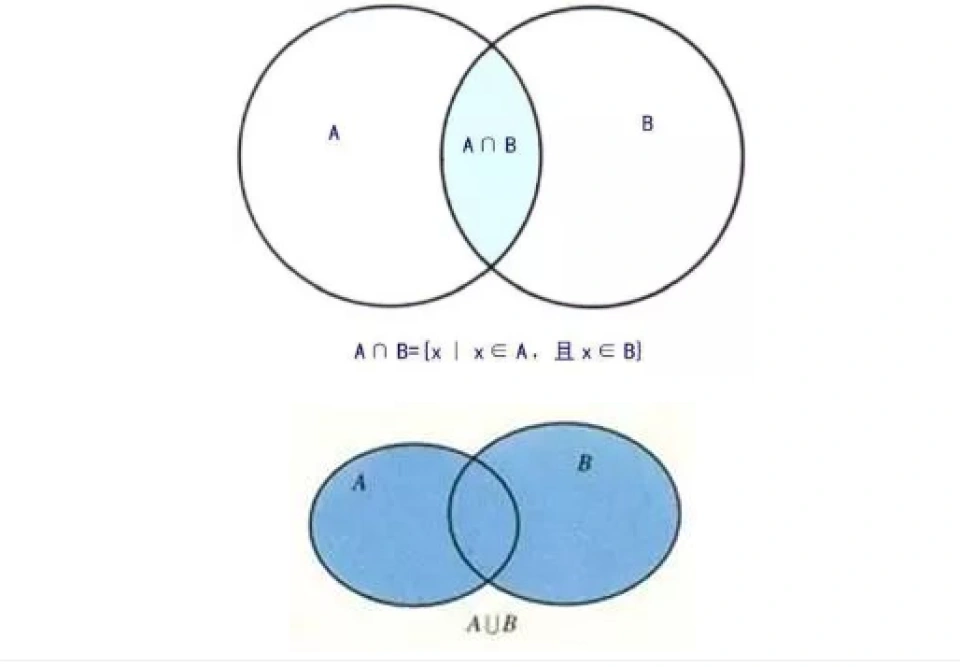
定义 1.5 设A,B为集合,A与B的并集A∪B,交集A∩B(可简写为AB),定义如下:
A∪B={x|x∈A或x∈B}
A∩B={x|x∈A且x∈B}
集合之间的关系和初级运算可以用韦恩图(也称Venn图或文氏图)来表示:
定义 1.6 在一个具体问题中,如果涉及的集合都是某个集合的子集,则称这个集合为全集,记作E(或U,I等),(符号并不固定,但是要明确谁是全集)。
定义 1.7 给定全集I,A⊆I,A在I中的补集,~A(或在A上面打一横线,如下图),定义如下:
~A={x∈I|x∉A}
我们常用|A|表示集合A中元素个数。
在Venn图中,我们常用平面上的封闭曲线的内部代表集合,这样集合之间的关系可以简洁明了的看出来,我们可以通过它快速理解一个重要原理:
容斥原理 设S是有穷集(元素有限),P₁,P₂,P₃,……Pₘ是m个性质.S中的任何元素x或者具有性质Pᵢ或者不具有性质Pᵢ,两种情况必居其一.令Aᵢ表示S中具有性质Pᵢ的元素构成的子集,则S中不具有性质P₁,P₂,P₃,……Pₘ的元素数为:
推论 S中至少具有一条性质的元素数为
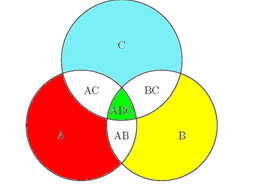
这一过程看上去很复杂,但是我们在如下Venn图中可简单运用:
|A∪B∪C| = |A|+|B|+|C |- |A∩B|- |B∩C| – |C∩A| + |A∩B∩C|
在Venn图中我们发现,AC,BC,AB被算了两次,所以我们减掉它们,但是ABC被减掉了三次,所以我们加上它。所以容斥原理就是
现在,我们再讲一个数学中的最基本方法之一——数学归纳法。
归纳公(原)理 设S是N的一个子集,满足条件:
1.1∈S
2.如果n∈S,则n+1∈S,
那么S=N.
归纳公理属于皮亚诺公理的一部分,这个公理给我们阐明一个重要原理。
第一数学归纳法 设P(n)是关于自然数n的一种性质或命题.如果:
1.当n=1是,P(1)成立;
2.由P(n)成立必可推出P(n+1)成立,
那么P(n)对所有自然数n成立.
证 设使P(n)成立的所有自然数n组成的集合是S.S是N的子集.由条件1可知1∈S;由条件2知,若n∈S,则n+1∈S.所以由归纳公理可知S=N.
Q.E.D.
这一过程告诉我们证明一个命题成立的思路:
首先保证取1d的时候成立;
其次,假设n成立,如果我们推出了n+1也成立,就说明该命题对所有自然数都成立。
说明 事实上,第一数学归纳法与归纳原理等价,因此我们又称之为数学归纳法原理,并把第一数学归纳法简称为数学归纳法。
既然有第一数学归纳法,就意味存在第二数学归纳法,不过现在我们得先引入一个原理:
最小数原理 设T是N的一个非空子集.那么,必存在t₀∈T,使得任意t∈T有t₀≤t,即t₀是T中的最小自然数。
第二数学归纳法 设P(n)是关于自然数n的一种性质或命题.如果:
1.当n=1时,P(1)成立;
2.对n>1,若对所有的自然数m<n,P(m)成立,则必可推出P(n)成立,
那么P(n)对所有自然数n成立.
证 用反证法.若定理不成立,设T是使P(n)不成立的所有自然数组成的集合,T非空.由最小数原理知集合T必有最小自然数t₀.由于P(1)成立,所以t₀>1.由条件2(取n=t₀)可知道,必有自然数m<t₀,使P(m)不成立(否则P(t₀)成立).由T的定义知m∈T,但这和t₀的最小性矛盾.
Q.E.D.
说明 实际上,第二数学归纳法与最小数原理等价。即第二数学归纳法也可以推出最小数原理,但它们同时也都可被第一数学归纳法证明,这也是他们之间的重要联系。还有一点需要指明的是,凡是数学归纳法证明的命题都可用最小数原理证明,但最小数原理无法推出归纳公理。
终于写完第一篇了,花费了我一天左右的时间,其实我在写的过程中一直在想到底要跟大家说什么,我怕某些地方讲的不清楚让大家不明白,也是琢磨了很久。不过,这个系列的开始也是一次非常激动的经历,至少在这个过程中,我的思维会更加清晰,写作能力也会上升,重点是我会更加自信,感谢博科给我这个机会,也希望大家多多支持!
参考资料:
百度百科、离散数学(第二版)(高等教育出版社)、离散数学(第五版)(清华大学出版社)、高中数学必修第一册、数学奥林匹克小丛书(第三版)数列与数学归纳法



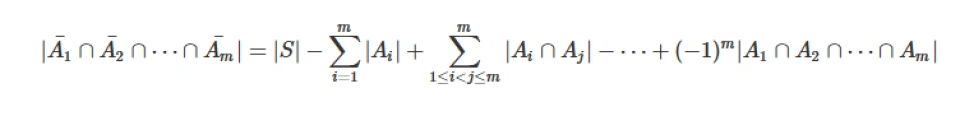
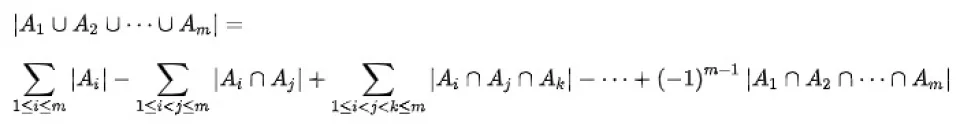


![[s-70]](https://www.bokeyuan.net/pic/image/emoji/cas/70.png)












