科普驿站 第九十期
科目: 物理
难度: B1
讲师: 星尘
(八十九期为《数学的故事》三、四部分,已将其放置在八十二期中)
光子晶体
在讲拓扑光子学之前,先给大家讲一个故事吧。
古时候有个祝家庄,祝家庄的祝员外有一个小女儿,名叫祝英台。祝英台天生聪明伶俐,纯真可爱,从小就喜欢读诗,爱好琴棋书画。她不甘世俗,女扮男装来杭州城的书院读书。路上遇到了出身平民的梁山伯。两人意气相投,结为异性金兰,情深义厚,直到两人约定成亲。但在梁山伯提亲前,祝英台就被许配他人,结果他因相思病逝,被安葬于南山。知晓此事的祝英台在迎亲队伍经过南山的时候跳入梁山伯墓中,和梁山伯化作两只蝴蝶从墓中飞了出来。蝴蝶的翅膀上闪耀着五彩斑斓的颜色。
我想,大家都见过美丽的蝴蝶吧。除了蝴蝶之外,自然界中的其他一些动物也存在绚丽的颜色。比如美丽的孔雀羽毛、爱伪装的变色龙。阳光下它们的表面呈现出光鲜亮丽的颜色。你们有没有想过,这些自然界中的颜色是怎么产生的呢?
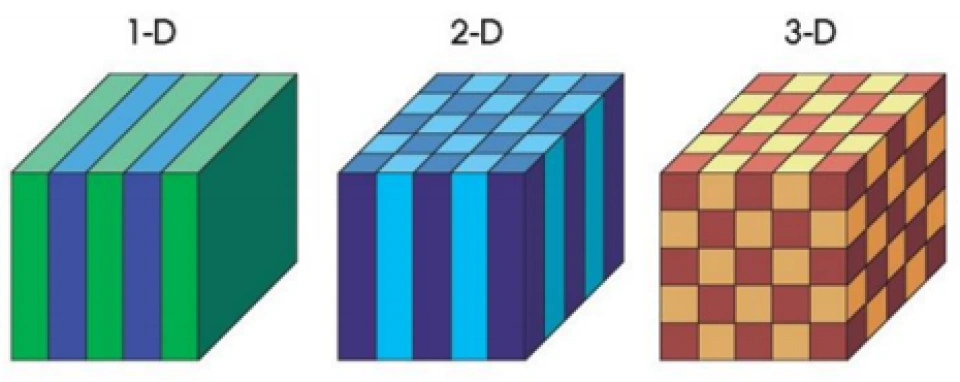
科学家们发现,这些颜色的产生源于周期性排列的微观结构。因其不同的尺寸而反射不同波长的光波,最终形成了我们看到的“五颜六色”。而变色龙之所以能够变色,也是因为它能够改变皮肤表面的微观结构。
科学家根据这个原理,设计制造出了一种周期性排列的微纳尺度光学结构——光子晶体。
受到布拉格散射的影响,某些频率的电磁波不能在光子晶体中传播。我们称这些频率的电磁波处于“禁带”之中。因此人们认识到可以利用周期排列的结构及非均匀介质等光学微纳结构对电磁波的传播进行设计和操纵。
例如,在二维光子晶体中引入“线缺陷”。通俗来讲就是挖去几个特定的结构单元在晶体中形成一条“隧道”。频率处于“禁带”中的电磁波就可以沿着这条“隧道”传输了。从而形成光子晶体波导。
大家可能对光导纤维(简称光纤)比较熟悉。光纤也是一种光波导。凭借其良好的传光性能,已经在汽车、医学、通讯、装饰、船舶等许多领域发挥了重要的作用。在一般的光纤波导中,传输光波利用的是全反射的原理,当波导弯曲程度较大时,传输效率就会降低。而在光子晶体弯曲的波导中,它可以克服大角度的限制。不论拐多大弯,都能保持原有的传输效率。
拓扑
另外一个概念是“拓扑”。
在讲“拓扑”的概念之前,我先给大家讲一个小故事。
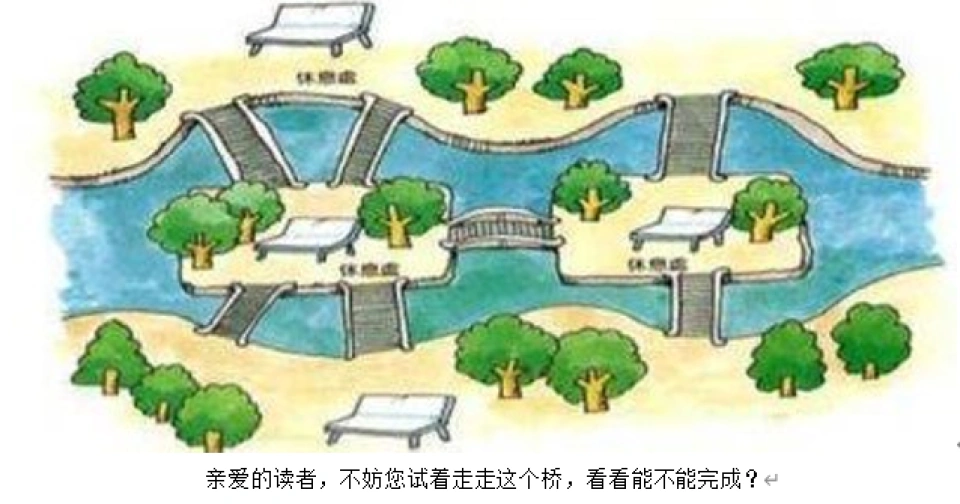
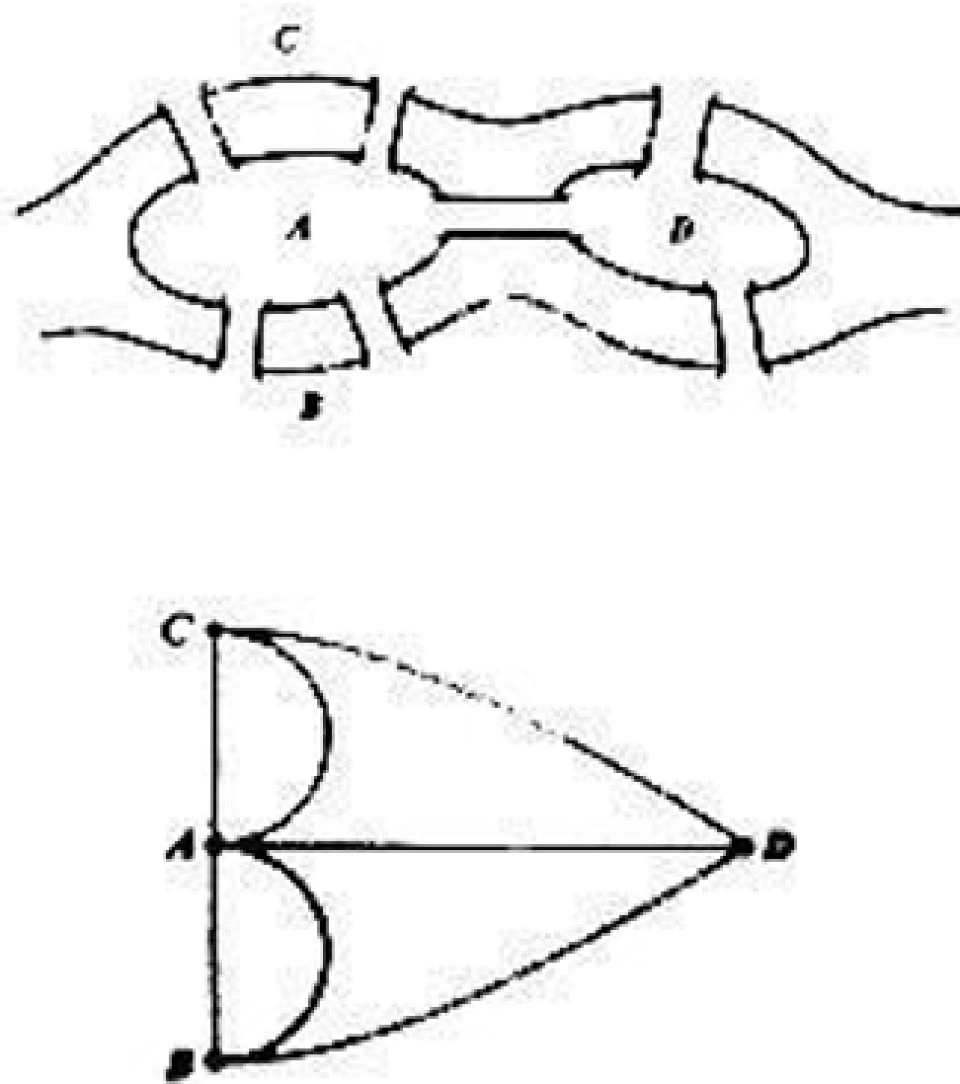
18世纪,在哥尼斯堡的一个公园里,有七座桥将普雷格尔河中两个岛及岛与河岸连接起来(如图)。人们经常在这里嬉戏玩耍。有人问道:是否可能从这四块陆地中任一块出发,恰好通过每座桥一次,再回到起点?人们尝试了许多方法,但最终没能成功。
亲爱的读者,不妨您试着走走这个桥,看看能不能完成?
后来人们带着这个问题找到了当时的大数学家——欧拉。欧拉经过一番思索,最终得出了结论。他首先把这个问题简化,即将两个小岛和河岸分别看成四个点,各个桥看作连接四个点的线。那么这个问题就简化为:能不能一笔把简化后的图形画出来。
最后欧拉经过一番推论得出结论:一笔把这个图形画出来是不可能的。
这就是拓扑学的开端。
为了让大家更好地理解拓扑的概念,在这里我举一个小例子。
这儿有六件物品。分别是:铅球、面包圈、眼镜框(没有镜片);勺子、杯子(有把手)、茶壶(无盖)。大家能不能根据它们的共同特征,把它们两两连接起来?
在没有接触过“拓扑”概念之前,你如果能找到答案,那么就说明你很有数学天赋。我们发现它们的共同特征是“洞”的数目:铅球和勺子都没有“洞”,而面包圈和杯子都只有一个“洞”,同样的道理,眼镜框和茶壶都各自有两个“洞”。可以说,铅球和勺子、面包圈和杯子、眼镜框和茶壶分别是拓扑等价的。或者换一种方式理解,举个例子,如果把面包圈看作一个存在一个洞的橡皮泥,而且这个橡皮泥自身是不发生粘合的,那么它可以捏成带把杯子的模样。而不同的拓扑类通过不同的“洞数”来区分,比如说一个没有洞的球,就不可能捏成一个带把杯子,所以铅球和杯子不能看成一类。而“洞数”在拓扑学中称为“亏格数”(Genus)。对于拓扑等价的物体来说,他们的亏格数是相同的,因此它是一种拓扑不变量。
形象地说,拓扑研究的是一块不发生粘合的橡皮泥捏成的各种形状。抽象而又严谨一点的描述就是:几何拓扑是研究几何对象在连续形变下的某种不变性。
拓扑光子学
之前讲过如果在光子晶体中引入“线缺陷”,就可以形成光波导。但这样的光波导也存在它固有的缺点:由于电磁波的波动性,除了正向传输的电磁波之外,会不可避免地产生反向传播的电磁波。这势必造成电磁波在传输过程中的损耗。
为了解决这个问题,2005年美国普林斯顿大学的Haldane等人将拓扑的概念引入光子学领域,开创了拓扑光子学的先河。从理论上展示了在旋电(Gyroelectric)材料柱构成的光子晶体中,通过加入沿柱轴方向的外加电场来打破电磁波传输的时间反演对称性。
关于“时间反演对称”的概念,我在这里做一个补充说明:时间反演好比是把一部电影倒放。而时间反演对称性是指,即使这部电影倒放了,仍然合乎逻辑,不会影响观赏效果。宏观世界中,由于熵增原理[ ],物理过程是不具有时间反演对称性的。但从微观来看,许多物理过程存在时间反演对称性。比如,电磁波在真空中传播时具有时间反演对称性。
Haldane等人提出的这种模式不仅使光波在光子晶体边界上定向传输成为可能,而且在弯曲或者有杂质的情况下传播不受阻碍。听起来可能有点深奥,那么做一个形象的比喻:往平静而又狭窄的河面上扔几颗石头,河面就会泛起涟漪向两头扩散。这时候水面吹来一阵风,就会促使水波顺风而行。而刚刚说的外加电场就相当于给光波加了一阵“风”,从而使光子晶体对于光波而言有了拓扑性质。这样的光子晶体可以看作是一种光学拓扑绝缘体。
关于在光子晶体中实现定向波传输的具体原理相当复杂,它被记录在2005年Haldane和Raghu写的一篇文章中。当时这篇文章被投稿到了Physical Review Letters(PRL)。但当时审稿人并没能看懂,这篇文章也迟迟没能被发表。直到2008年Haldane和Raghu写了一篇长达20多页的解释之后,文章才得以成功发表。
然而理论中的做法在实际中很难推广。原因在于天然材料的旋电性不强,对系统时间反演对称性的破坏强度有限。 所以在现实中这种做法很难实现。好比是理论上只要找到一个合适的位置,就能让鸡蛋在桌子上立起来,但由于平衡位置太小,在现实中很难实现。
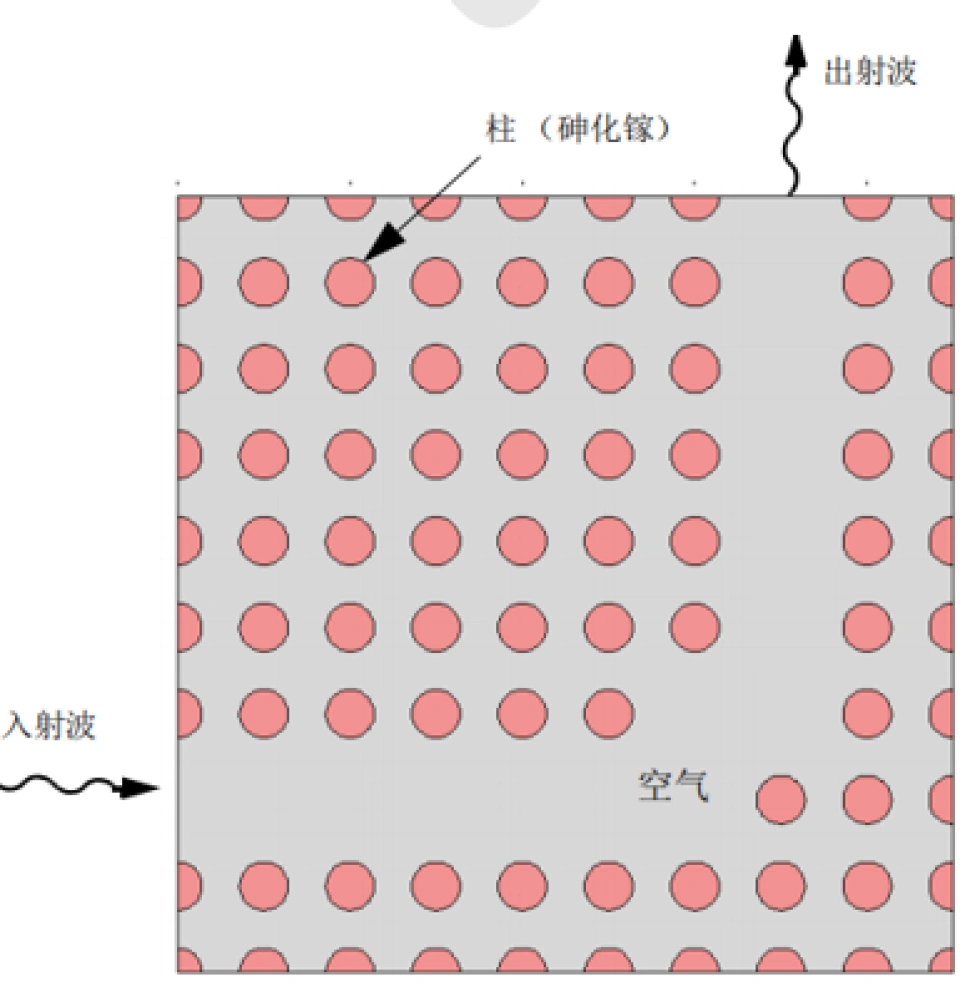
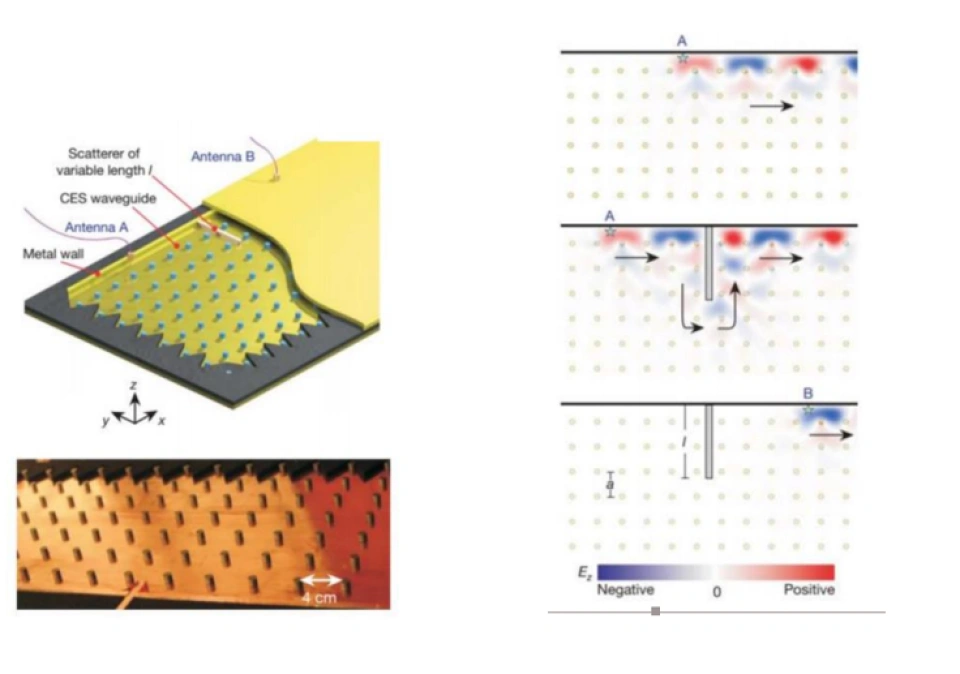
2008年,TIM的Wang等人提出了另外一种方案,即使用旋磁材料来代替旋电材料。首次通过实验观测到拓扑保护的单向波导的传输,并且对它进行了模拟仿真。从而证实了Haldane等人的预言。下图是利用旋磁柱构造光学拓扑态的实验装置和模拟仿真结果。
可以注意到在实验装置中他们放置了一个Scatterer(散射体),相当于引入了一个阻碍。我们可以看到,光在传播过程中绕过了这个阻碍而没有被反射,很好地完成了单向传播。这也印证了我们之前说的,光沿光学拓扑绝缘体传播时,不怕杂质或阻碍的干扰。
前面提到,从拓扑学的角度看,不同物体所具有的“孔洞数”称为“亏格数”。在拓扑光子晶体中,也有与“亏格数”相对应的物理量,我们称之为“陈数”(Chern number),它也是一种拓扑不变量。对于一种拓扑光子晶体,如果可以让某种电磁波正向传播,那么可以称它的陈数为1;相应地如果另外一种光子晶体能够传输相反方向的某种电磁波,那么它的陈数就为-1。
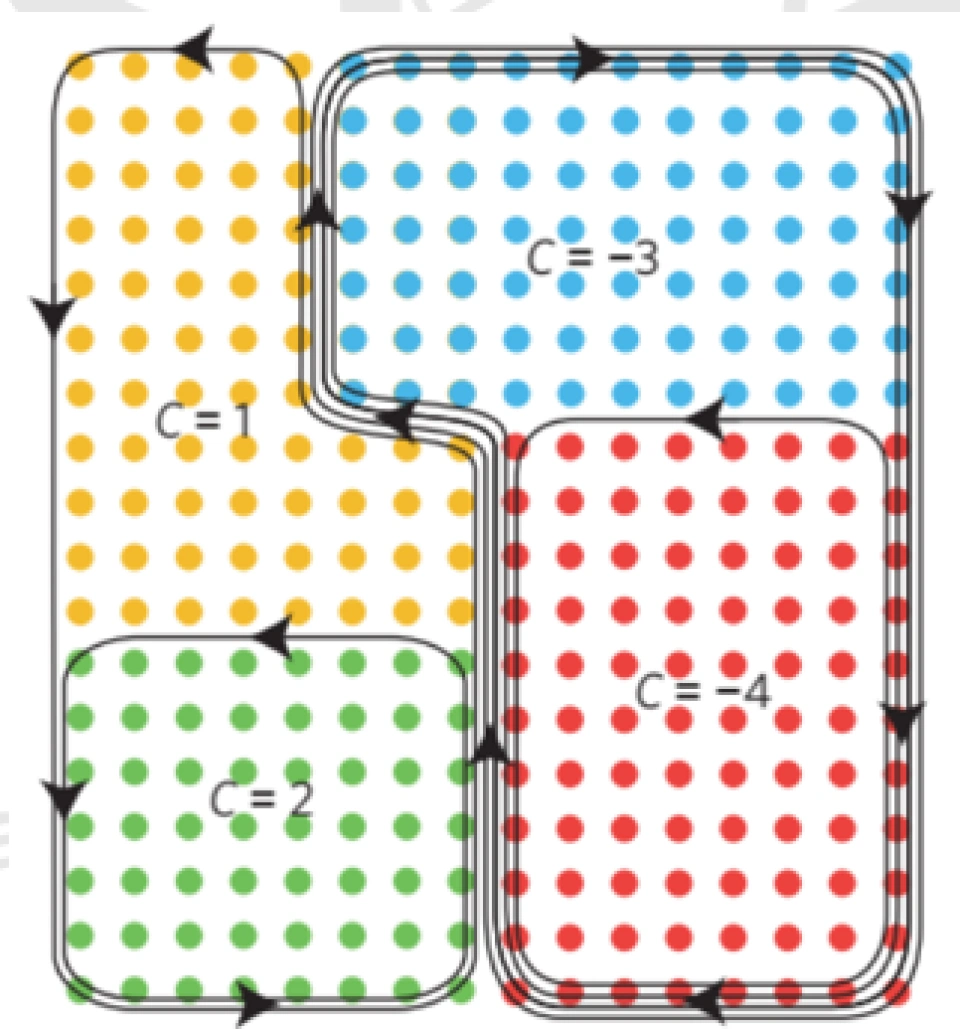
2014 年,Skirlo 等人利用巧妙的方法从理论上实现了高陈数的光子带隙。2015年,他们从实验上验证了“高陈数”的特性。下图是他们提出的单光子回路示意图。
从图中可以看到,他们设计的结构可以实现陈数(C)分别为1,2,-3,-4的光学拓扑态。
近十几年来,拓扑光子学已经在很多领域取得了巨大的发展,除了外加磁场的方法,人们也发明了各种其它新颖的方法来实现光场调控。实现了无反射的拓扑波导、拓扑分波器、拓扑激光器等许多应用,从而使光学器件获得了高保真的传输性能。当然还存在许多未知等待着你们探索和挖掘。
【本文为耀星会作者的原创作品,未经允许,禁止盗用、转载、篡改文章,否则耀星会和作者将追究版权责任。】