月牙面积定理
月牙形是一种边缘为两个圆弧的平面图形。公元前5世纪古希腊希俄斯的希波克拉底(Hippocrates of Chios)因为他的伟大发现——求月牙面积——而被后人赞颂。评论家普罗克洛斯(公元410—485)就以他5世纪的眼光认为,希俄斯的希波克拉底“……作出了月牙形的等面积正方形,并在几何学中做过许多其他发现,如果说那个时代有一位作图天才,那一定非他莫属。” William Dunham 在他的科普名著《天才引导的历程:数学中的伟大定理》中,讲述了12个伟大的定理,而第一个定理就是希波克拉底的月牙面积定理。
那么今天我们将给大家介绍一下月牙面积定理及其历史背景和意义所在。
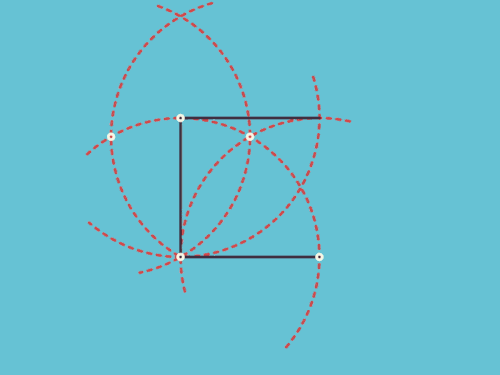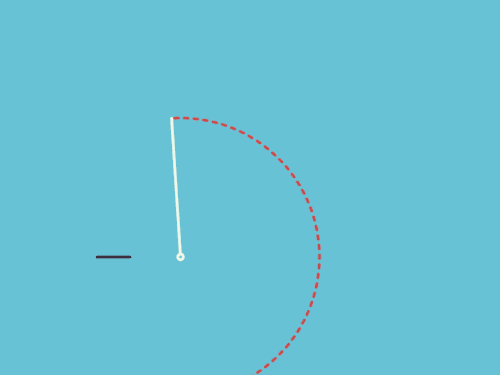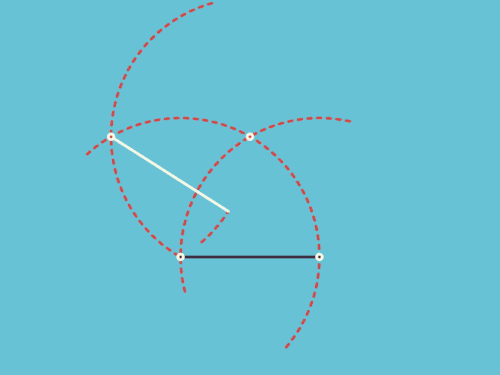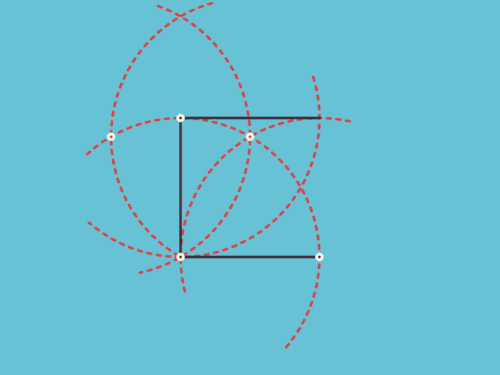
如图,以AB为直径作半圆,O为AB的中点,作OC垂直于AB,其交半圆于C,并连接AC与BC,取AC的中点D,然后以D为圆心,以AD为半径作半圆AEC,这样就形成了月牙形AECF,如图中的黄色部分。
希波克拉底发现并证明了月牙面积定理。
【定理】 月牙形AECF可用等积正方形表示。
这里有必要解释一下“可用等积正方形表示”,字面意思就是“能够用与其面积相等的正方形表示”。但是为什么要用等积正方形表示呢?其实这里面有着深刻的历史背景和意义,体现出了古希腊人独特的数学智慧。
对于古希腊人说,求面积源于实际生产生活中测量的需要,如何求各种图形的面积——尤其是不规则图形的面积——是那个时代希腊数学的一个中心问题。他们的处理方法简单而伟大,即把不规则图形用等面积的正方形替换,那么确定不规则图形的面积问题就转化为确定正方形面积的简单问题了。
因此,对于公元前5世纪的希腊人来说,如果一个平面图形能够用一个等积正方形表示,那么平面图形的面积就可以确定下来了。所以求面积也叫求方。在求方的过程中,古希腊人还有一个不成文的规矩,就是只能使用圆规和(没有刻度的)直尺作图,而且这个规定一直保留至今,甚至成为几何作图必须遵守的规则。
这种化繁为简,用简单和基本的东西为基础构建复杂问题的处理方式,在数学中有广泛的应用,也是我们在数学学习中需要掌握的重要数学思想。
古希腊人首先解决了长方形求方的问题,接下来是三角形求方问题,最后过渡到多边形求方问题。
【第1步】求长方形的面积。
对任意长方形ABCD,延长AD到E使DE=CD,取AE的中点F,以点F为圆心,以AF=EF为半径作半圆,延长CD交半圆于H,然后以DH为边作正方形DHKL,那么,正方形DHKL与原长方形ABCD面积相等。
为了证明正方形DHKL面积与长方形ABCD面积相等,我们设HF=a,DF=b,DH=c。则在直角三角形DFH中,根据勾股定理:a²=b²+c²,或a²-b²=c²。显然AF=EF=HF=a,AD=AF+DF=a+b,CD=DE=EF-DF=a-b,所以
S(长方形ABCD)
=AD×CD
=(a+b)(a-b)
=a²-b²
=c²=S(正方形DHKL)
这样,我们就证明原长方形面积等于我们用尺规作图所作的正方形面积,从而完成了长方形的求方。
求出长方形的面积后,我们就可以求三角形面积了。
【第2步】求三角形面积。
对任意三角形ABC,作BC边上的高AD,取AD的中点E,然后我们作长方形FGHI,使FG=BC,GH=DE。
此时,S(长方形FGHI)
=FG×GH
=BC×DE
=1/2BC×AD
=S(△ABC)
至此,三角形求方问题也已完成。
【第3步】求多边形的面积。
对于任意一个多边形,我们可以通过连接对角线将多边形分成若干个三角形。以五边形为例,可以将其划分为3个三角形,即Ⅰ,Ⅱ和Ⅲ,整个五边形的面积就等于S(Ⅰ)+S(Ⅱ)+S(Ⅲ)。
在第2步中,我们已经知道三角形是可用等积正方形表示的,因此,我们可以分别作出与Ⅰ,Ⅱ,Ⅲ面积相等的正方形,设它们的边长分别为a,b,c,如下图。
然后,以a和b为直角边,作直角三角形,设其斜边长为x,则x²=a²+b²。再以x和c为直角边,作直角三角形,设其斜边长为y,因而,y²=x²+c²。最后,我们便 能以y为边长作正方形(如下图阴影部分)。
综合我们的结论,就得到
y²=x²+c²=a²+b²+c²
=S(Ⅰ)+S(Ⅱ)+S(Ⅲ)
因此,原多边形的面积就等于以y为边长的正方形面积。
显然,以上作图和推导过程适用于任何多边形。总之,多边形是可用等积正方形表示的。即使对于像下图这样的平面图形也是可以用等积正方形表示的。想想为什么?
利用上述方法,希波克拉底时代的希腊人可以将杂乱无章的不规则多边形变为等面积正方形。但是,遗憾的是这些图形都是直边图形,对于曲边图形是否也可用等积正方形表示这个问题,起初,人们认为,这似乎是根本不可能的,因为显然没有办法用圆规和直尺将曲线拉直。其中,尤其是对于圆来说,如果不能用等积正方形表示,总是不那么完美。
我们都知道,几何上有三大著名难题,这三个问题是:
1. 三等分角,将给定角分成三个相等的角问题;
2. 倍立方体,求一体积为已知立方体体积两倍的立方体的边长;
3. 化圆为方,求与给定圆面积相等的正方形问题。
其中化圆为方问题正源于此。
当希波克拉底于公元前5世纪成功地将一种称为“月牙”曲线图形化为正方形时,世人惊得目瞪口呆。
由于希波克拉底求月牙面积的成功,希腊数学家对于“化圆为方”问题持非常乐观的态度,仿佛胜利的曙光就在眼前,据传希波克拉底本人曾声称他能够求出圆的面积。不过戏剧性的是,2000多年后的1882年,德国数学家费迪南德·林德曼(1852—1939)成功而明确地证明了化圆为方是根本不可能的。这真是一个漫长、曲折而又颇具戏剧性的结果。
林德曼因为证明π是超越数,从而导致化圆为方不可能问题的证明,这已经超出了本文所要讨论的范围。
最后,我们在下方附上希波克拉底月牙面积定理的证明,他的证明是如此简单而又高明。
【定理】 月牙形AECF可用等积正方形表示。
【证明】 由于∠ACB为半圆上的圆周角,所以,∠ACB是直角。根据“边角边”全等定理,三角形AOC和BOC全等,因此,AC=BC。然后,我们应用毕达哥拉斯定理(即勾股定理),就得到
因为AB是半圆ACB的直径,AC是半圆AEC的直径,所以,我们可以应用上述第三条结论,即得到
也就是说,半圆AEC的面积是半圆ACB面积的一半。
我们现在来看四分之一圆AFCO。显然,这个四分之一圆也是半圆ACB面积的一半,据此,我们可直接得出
面积(半圆AEC)=面积(四分之一圆AFCO)
最后,我们只需从这两个图形中各自减去它们共同的部分AFCD,即
面积(半圆AEC)-面积(AFCD部分)
=面积(四分之一圆AFCO)-面积(AFCD部分)
我们从图中可以很快看出,剩下的部分就是
面积(月牙形AECF)=面积(△ACO)
我们已经知道,可以作一个正方形,使其面积等于三角形ACO,因而也等于月牙形AECF的面积。这就是我们所寻求的化月牙形为方的问题。证毕.
以上,希波克拉底只是求出了一种特殊的月牙形面积,有趣的是,并不是所有的月牙形都能化成等积正方形。1771年,伟大的数学家欧拉(1707—1783)发现了另外两种可以用等积正方形表示的月牙形。直到20世纪,N.G. 切巴托鲁和A.W. 多罗德诺证明出了只有五种月牙形可用等积正方形表示!所有其他类型的月牙形,都像圆形一样,不可能化为等积正方形。
最后,需要说明的是,根据希波克拉底特殊月牙定理的证明,我们很容易证明如下更一般的月牙定理。
【月牙定理】
以直角三角形两条直角边为直径向外做两个半圆,以斜边为直径向内做半圆,则三个半圆所围成的两个月牙型面积之和等于该直角三角形的面积。
即两个黄色月牙形面积之和等于灰色直角三角形面积。作为练习,各位读者可以试着自己完成证明过程哦。
图文来源:好玩的数学(ID:mathfun)
本文已获得授权,转载请联系原作者。
责任编辑:一毫秒的永恒
APC科普编辑部


![[s-1]](https://www.bokeyuan.net/pic/image/emoji/cas/1.png)












