科普驿站 第八十六期
科目:物理
难度:B1
讲师:莫特相变的皮卡丘
4 超导的经典解释
所有人都想知道这是为什么。有一对德国人,叫做伦敦兄弟,没错就是英国首都那个London,尝试用经典的方法解释超导的两个效应。下文将用伦敦指代这两兄弟。针对零电阻的方程比较简单,我将在这里推导伦敦第一方程。
伦敦认为,超导电流包含两部分,为了方便起见,我们使用电流密度j(粗体代表矢量)——也就是单位面积上流过的电流(类比电阻率的定义)。其中的第一部分为正常电流jn,另一部分为超导电流js。那么有总电流密度
电流是矢量呀,也就是有大小和方向的量,所以带了箭头。这里的矢量箭头,表示电流方向与电场方向相一致,不方便理解就可以直接无视。
对于正常电流,其与电场强度的关系满足欧姆定律
实际上就是电流密度=电阻率×电场强度。(中学的欧姆定律I=U/R,利用电阻的微观定义R=lρ/s,有I=Us/(lρ)。两边同时除以s,左边为电流密度j=I/s,右边电场强度E=U/l,然后定义电导率为电阻率的倒数,σ=1/ρ,就得到了j=σE)。
而对于超导电流,由于不存在电阻,欧姆定律将不能得到满足,电子的运动由牛顿第二定律所确定,即
其中的电场力
利用电流的微观定义,也就是,电流是由电荷定向流动产生的。知
这里的js是超导电流,n是超导电子的数目。伦敦假设这个数目n只与温度相关。这个式子两边取Δ得到
注意到电子数目与元电荷都是常量。将这些带入上面的牛顿第二定律与电场力表达式,得到
伦敦第一方程告诉我们,在超导体中,电流的变化速率与电场成正比。对比传统的导体,我们发现欧姆定律告诉我们电流本身与电场成正比。显然超导电流与经典电流的电学性质存在很大差异。
伦敦第二方程是针对迈斯纳效应的,实质上是将著名的麦克斯韦方程带入第一方程得到的。麦克斯韦方程组有四条,分别讲述电场的形成(电荷)、磁场的形成(很遗憾没有磁单极子)、涡旋电场激发随时间变化的磁场和涡旋磁场激发随时间变化的电场——这四点实际上大家高中都学过。大家觉得要带入哪一条呢?很显然是后两条中的一条。为了避免重复计算对时间的变化(也就是求二阶导数),选择第三条吧,这一条长这样
左边的倒三角+叉乘表示,计算电场强度 绕着一个点的旋转程度,就是大家经常用右手定则比划的那个旋转。右边代表磁感应强度随着时间的变化。结合伦敦第一方程,可以得出结论:
这个方程说明左边中括号内的式子对时间求导为0,也就是说,中括号以内的内容不随着时间变化而变化。所以,只要满足关系
也就是说,内部的涡旋电流激发了一个与外磁场等大反向的磁场,这样超导体内部区域的磁感应强度就保持为0了。
这个关系是楞次定律:超导体放进磁场的一瞬间,由于变化的磁场产生电场,这个电场引发的涡旋电流瞬间产生了一个磁场,并阻碍外磁场的增加。与普通导体不同的是,超导体不存在电阻,涡旋电流就不会消失,导致阻碍磁场一直存在。这就不难理解为什么将超导体放入磁场内,其内部将排除全部的磁力线了。
5 当经典理论遇到了问题
伦敦方程在解释直流零电阻与迈斯纳效应时,有较好的符合度,然而这个方程与实验还存在一些差别。首先,从微观角度讲,超导内部的磁场并不严格为0,而是一个从边界到内部指数衰减的关系,而表面这一段磁场不为0的距离极短,叫做穿透深度。根据伦敦第一方程对超导电子数量n的假设,穿透深度与温度有关。对于一般的金属,伦敦方程的理论计算表明,这个深度在10−6cm数量级,也就是几十nm的深度,相比金属而言几乎可以忽略不记。然而实验测出来的这个深度,的确与温度有关,但有时候比理论计算大好几倍,这里就出现了问题。
然后,人们很快发现迈斯纳效应也出现了问题。有些超导体在外加磁场增强的时候,内部的特定区域出现了磁感线,被叫做第二类超导体。这类超导体通常是复杂的合金,比如念起来像顺口溜的钇-钡-铜-氧体系。然而问题在于,随着外加磁场的连续增加,这些磁感线的数目并不是连续变化,而是像台阶那样发生跳跃,这种现象叫做磁通量子化。随着外加磁场持续增加,迈斯纳效应消失。由于磁感线出现的区域是特定的,于是赫赫有名的苏联理论物理学家朗道和合作者金兹堡将磁场B与位置r考虑了进去,他们认为超导电子数量n与温度、磁场与位置均存在关系。
列夫·朗道,对于学物理专业的同学而言,是一个又爱又恨的名字。这位理论大师有许多著名研究,涵盖现代物理各大方面,包括量子力学的密度矩阵、二级相变、磁性理论、超导与超流,甚至还有粒子物理的弱相互作用CP守恒性。苏联人给朗道做了一块大理石碑,将朗道的科学贡献列了十项,叫做“朗道十诫”。
说个题外话,朗道在历史上也许不能与摩西相提并论,但他(和他的学生)编写了一套十本理论物理教材,被认为是最权威的理论物理教材系列,难度大但很有调理,深受全世界学生喜爱。这位大佬甚至有很多轶闻趣事,包括对物理学家贡献排序的“朗道分级”,“刁难”学生的极难入学考试“朗道势垒”,还有在“大清洗”中被捕入狱然后因为玻尔等人的求情被放的神奇经历。
说回主题,朗道和金兹堡对超导提了一个方程,也就是刚刚提到的,自变量包含温度、磁场与位置的方程。问题来了,这个方程太难解了。
微分方程与常规的代数方程差不多,解决多元方程的思路通常是要分离变量。而金兹堡-朗道方程坏就坏在,这些自变量是相互耦合的,不能互相分开。无数的物理学家和数学家们前仆后继地计算这些方程,成功解决了前面的两个矛盾,关于穿透深度与磁通量子化。然而新的问题也出现了,金兹堡-朗道方程对更低温度的解释不大好,作为对比,之前的伦敦方程对更强磁场的解释不大好。大家有没有想到一个类似的著名矛盾事件?其实就是著名的“两朵乌云”中的一朵,黑体辐射,也是高温与低温两边的结果相互矛盾,最后引发了量子物理的革命。所以超导是不是也涉及量子呢?
我们仔细想想伦敦与朗道的方程,有没有觉得缺了什么?对了,这两个理论都在试图提出一个数学模型,并用这个数学模型去拟合未知的物理现象,然后发现这个数学模型和实验结果很相符。
6 BCS理论:当电子团结起来
实际上这个数学模型在物理上叫做唯象学。我们常说物理靠两条腿走路,一条是理论物理,一条是实验物理 ——事实上,唯象也是很重要的一个方面。这个学科在极端理论主义者眼中可能更偏实验物理,认为他们是处理数据的;而在一线实验者眼中,唯象又更偏理论。从物理史的角度,唯象学家最伟大的一次成就,是普朗克将黑体辐射公式里面的积分号改成了求和号,直接拉开了量子物理的序幕。普朗克很幸运,他为自己的唯象模型提出了解释:能量量子化,并且很快得到大量的实验验证。可惜超导的微观解释并不是来自于朗道与金兹堡的理论,而是来自一个被忽视了很久的因素:突变。
我们回到之前引入的问题:电阻突然降到0,我们可以联想到什么现象呢?物理里面的突变并不多,大部分情况是连续性变化的,例如速度和长度的变化。这很好理解,如果长度或者速度会突变,这一定涉及到一个超过光速的问题,是不可能发生的。但是有另一些突变的例子是大家都很熟悉的,例如水的沸腾与结冰。有一种过冷水,只要容器和水十分洁净,就可以对其静置降温,甚至可以降到零下十多度。然后,往桌子上一拍,就会瞬间结冰,十分壮观。
水结冰,或者是沸腾,这种现象叫做相变。“相”也就是物相,例如水在固液气三态变化。对于极低温的情况,有另一种相变,叫做玻色-爱因斯坦凝聚。在统计物理,原子等微观粒子按照组成成分可以分为两类,分别是满足费米圭狄拉克统计规律的费米子,与玻色-爱因斯坦统计规律的玻色子。这两种粒子分别与自然数中的奇数与偶数对应,由奇数个费米子组成的粒子为费米子,例如单个质子(事实上是3个夸克,仍然是奇数个)组成的氢原子核;由偶数个费米子组成的粒子为玻色子,例如包含两个质子和两个中子的He-4原子核。电子只由一个电子组成(没有微观结构),因此电子是费米子。这两类粒子的区别很大,最重要的一个区别,是费米子满足泡利不相容原理。
因此,当对物质降温时,其中原子的能量都会降低。对于玻色子所组成的物质,例如液态He-4,当温度降到极低时,所有原子的能量都会降低到基态,形成一种极其特殊的物态,叫做著名的玻色-爱因斯坦凝聚,缩写为BEC。处在BEC状态的液态He-4有一种叫做超流的性质,直接失去流动阻力,并且有比室温下的金属铜好800倍的超高导热性。不要小看这个没有流动阻力的特点,这意味着,超流的液态He-4甚至可以从玻璃容器的分子间隙里面毫无阻碍地流出来!朗道就发现他的一杯超流He-4漏得到处都是。
这时候我们有要素察觉了!处在BEC状态下的液态He-4存在无阻力流动的性质,是不是和超导很相似?然而电子是费米子,费米子受到泡利不相容原理的约束,无法全部达到能量最低的基态。从我们能带论的描述,电子的能量会展宽为一个带。似乎对超导微观理论的探究走入了僵局。接下来的另一件事情,给了人类巨大的启发:同位素效应。
1950年,人们发现,对于原子质量M不同的同位素,发生超导相-正常相转变的温度Tc满足关系:TcMα =常数。
对于一般的元素,指数因子α=0.5。这个同位素效应告诉我们,材料原子(晶格)本身的质量直接影响到超导。这和我们传统的想法完全不一样,包括之前的能带论,我们讲电子的能量来自于其本身的动能,以及电子与材料中原子核的势能,与质量有什么关系呢?于是人们很快意识到,超导电性的根源,是电子-晶格振动的相互作用。也就是说,参与相互作用的不是静止不动的晶格,而是晶格的振动!同一年,弗列里希指出,两个电子之间通过交换声子发生间接的相互作用。什么是声子呢?“声”实际上就是晶格的振动,类比光子,声子就是这个振动能量的传播子(声子并不是真正的粒子,提出声子的概念是方便计算与理论推导)。关键在于,一个电子放出声子后,被另一个电子接受,这个过程表明,在某种条件下,两个交换声子的电子可以相互吸引!
想象一下,其中的一个电子发出声子,并吸引晶格离开了原来的位置,接下来这个电子走掉了,晶格还来不及通过振动回到原位。此时离开原来位置的晶格又吸引了另一个电子靠近它。从整体上讲,就相当于两个电子相互吸引了。为了使能量降低,这两个电子动量与自旋恰好相反。
所有的问题都解决了:在温度极低时,部分电子在交换虚声子所引发的吸引力作用下,按照相反的动量与自旋两两结合成电子对,这种电子对通常称为库伯对——也就是BEC中的C。在这种情况下,这些电子对变成了玻色子,从而可以毫无阻碍凝聚在最低能量上,毫无阻碍地进行导电。于是超导的问题就迎刃而解了。
参考资料:
第4部分,London方程的推导,详见黄昆《固体物理》以及郭硕鸿《电动力学》
【本文为耀星会作者的原创作品,未经允许,禁止盗用、转载、篡改文章,否则耀星会和作者将追究版权责任。】


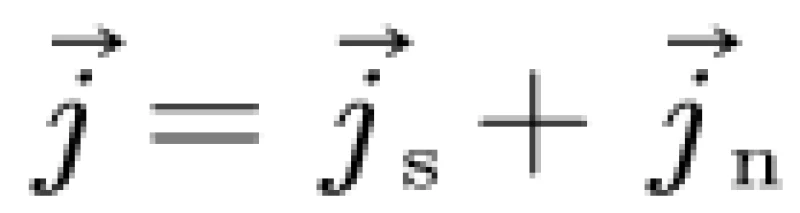
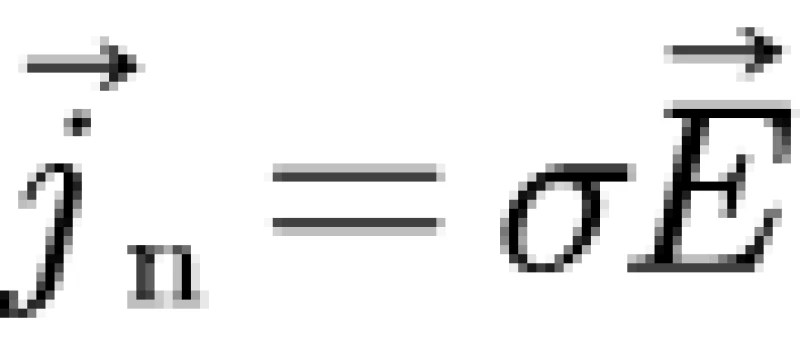
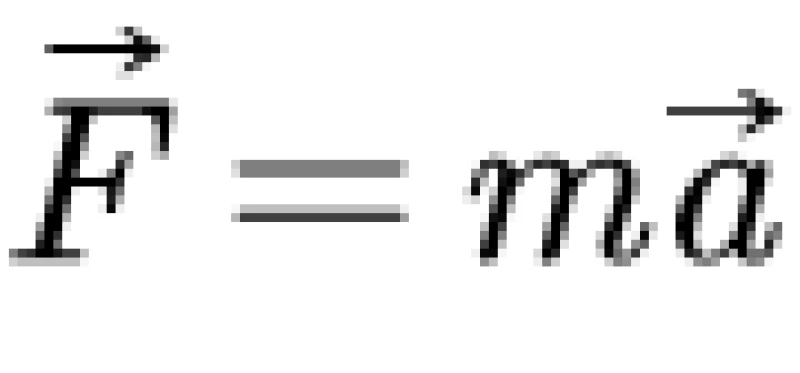
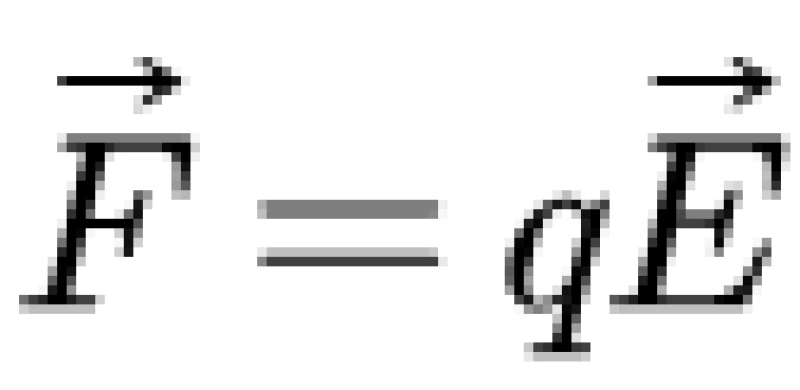

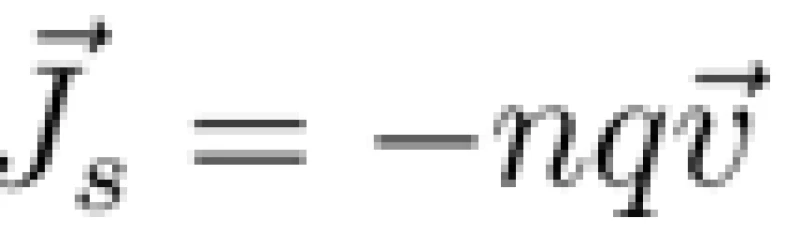
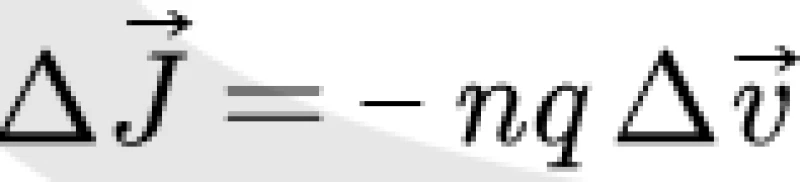
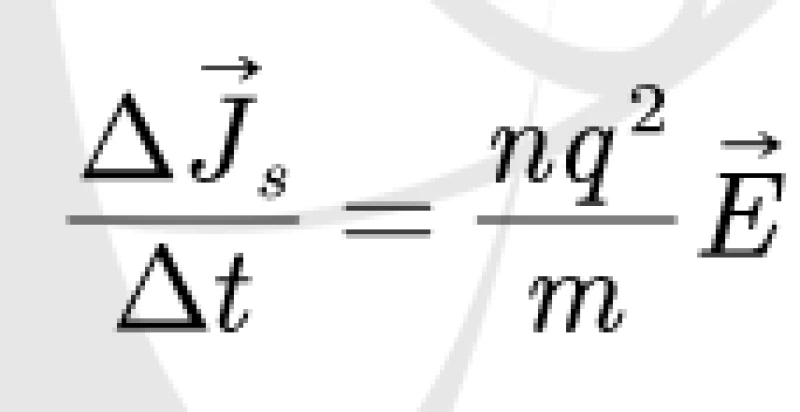
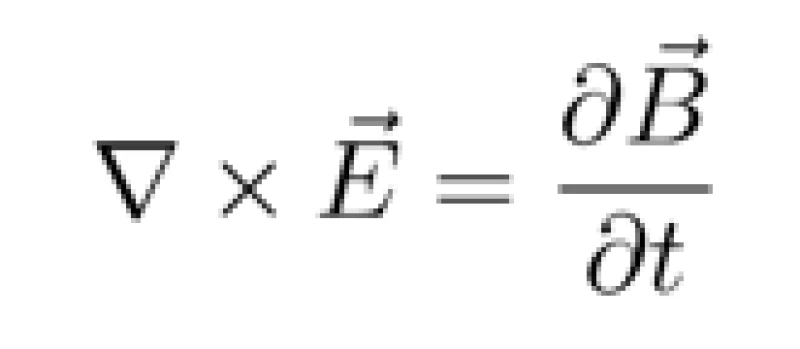
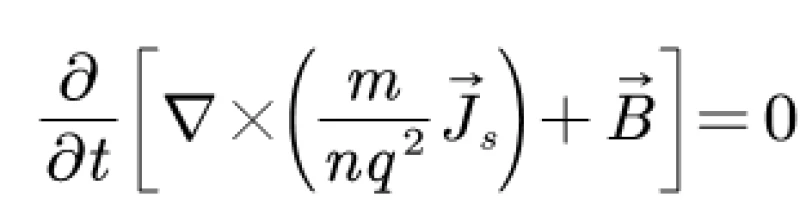
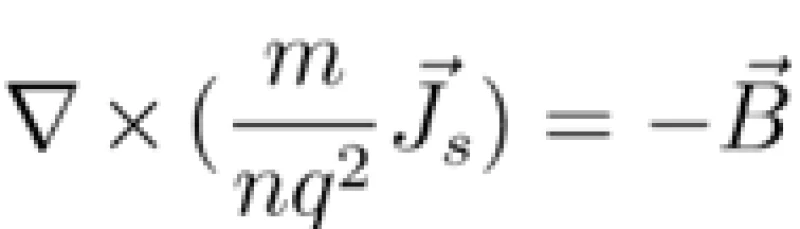


![[s-70]](https://www.bokeyuan.net/pic/image/emoji/cas/70.png)











