作者:phy-东西
审核:水缸
1、 问题描述
“注水定理”解决的是信息论中的一个基本问题:以总容量最大化为目标的AWGN信道功率分配方案优化。该问题描述如下:有 K 个并联 AWGN 信道且噪相互声独立,噪声功率依次为 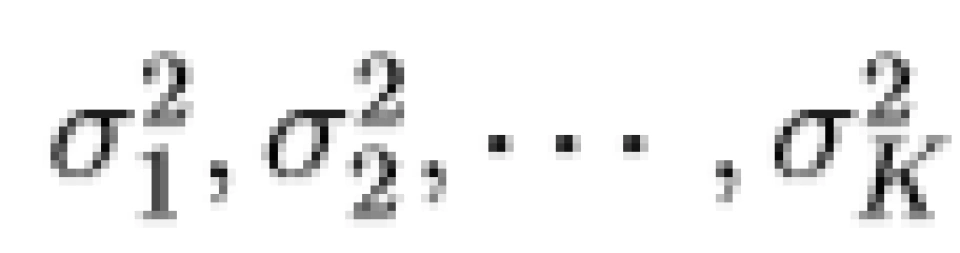 。总功率受限于 P,求出使 K 个并联信道功率最大化的功率分配方案。
。总功率受限于 P,求出使 K 个并联信道功率最大化的功率分配方案。
写做优化问题格式为:
(1.1)
2、 一个简单的证明
在这一节中我们给出一个比较便于理解的推导。
有的人可能觉得直接将所有功率分配到最好的(噪声功率最小的)信道里就可以,但信道容量的表达式是 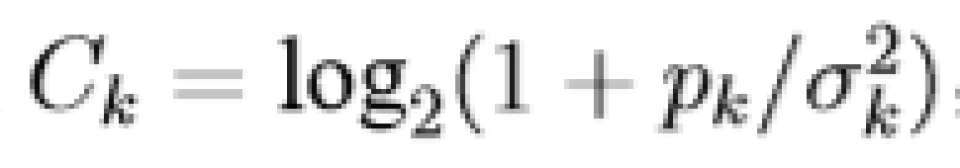 ,随功率增加,增长的幅度越来越小,这种想法启发我们每次将功率分配到容量增长幅度最大的信道中。
,随功率增加,增长的幅度越来越小,这种想法启发我们每次将功率分配到容量增长幅度最大的信道中。
假设我们已有一个初始功率分配方案 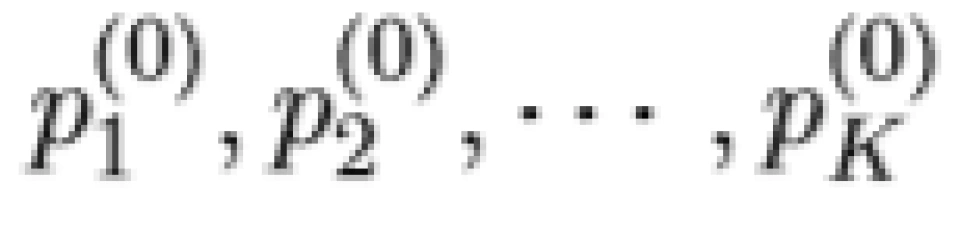 ,满足:
,满足:
显然  也是一个合理的初始化方案。假设一正数代表接下来要分配的功率:
也是一个合理的初始化方案。假设一正数代表接下来要分配的功率:
若把 δ 功率分配到第 k 个信道中,则信道容量增加:
(2.1)
不难发现应该将功率分配到 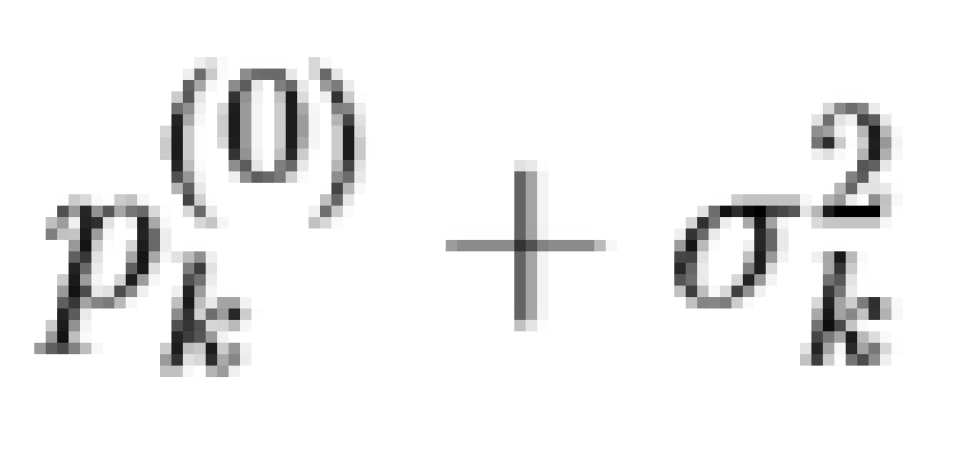 最小的信道中。如果每次选取的 δ 尽可能小,则将功率完全分配后,一部分信道的功率分配满足
最小的信道中。如果每次选取的 δ 尽可能小,则将功率完全分配后,一部分信道的功率分配满足 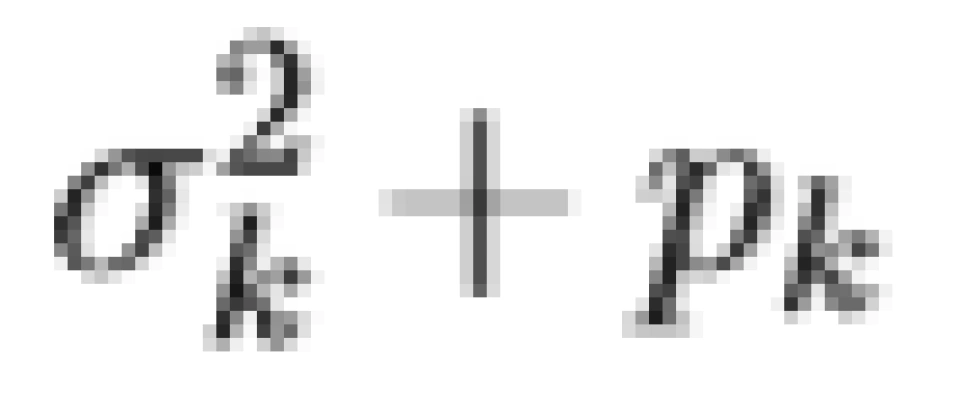 为定值,对于另一部分较差的(噪声功率较大的)信道,
为定值,对于另一部分较差的(噪声功率较大的)信道,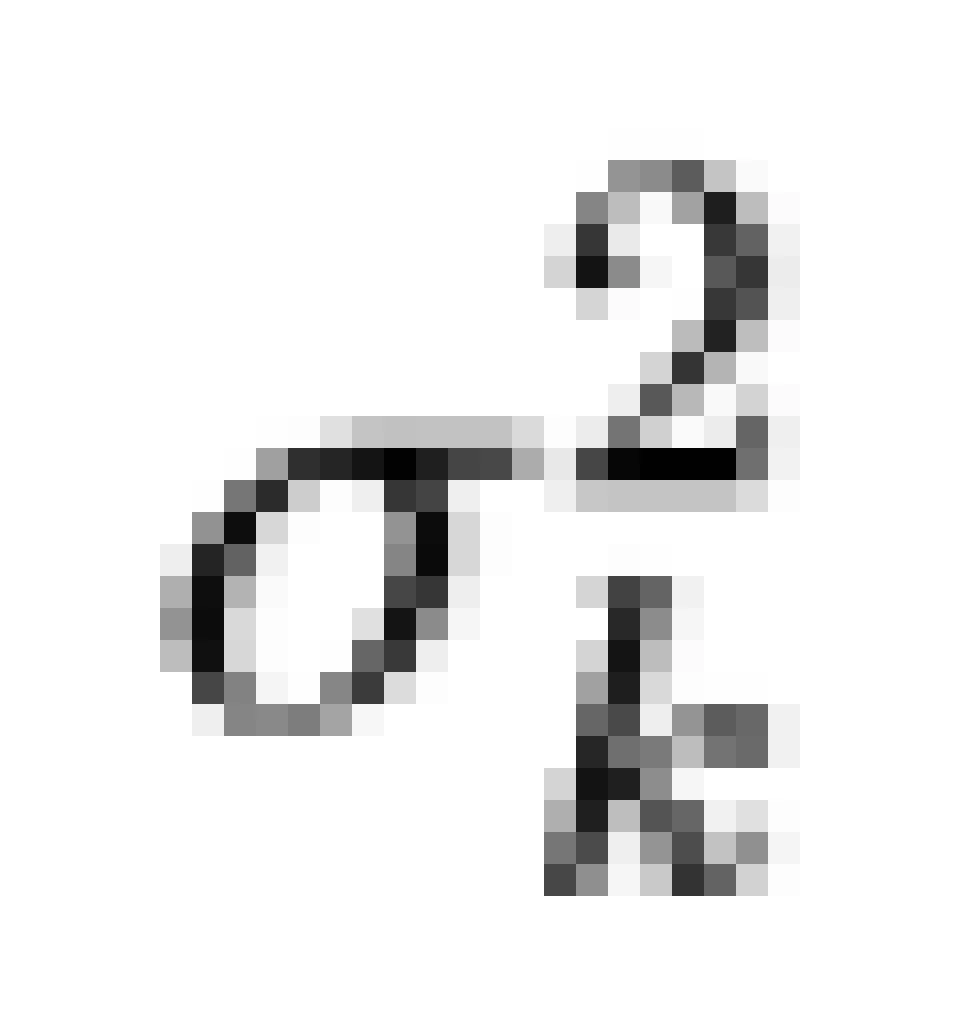 大于该定值,则不分配功率,即:
大于该定值,则不分配功率,即:
(2.2)
如果对于某一个分配方案若
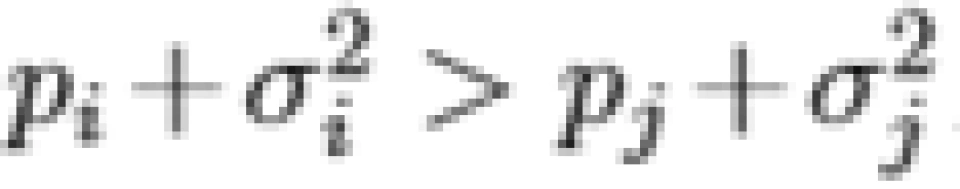 ,我们置
,我们置
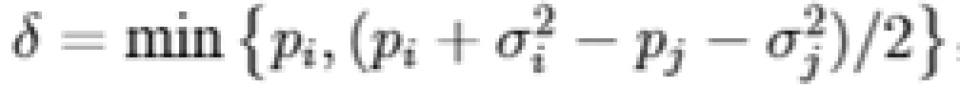 ,对于状态
,对于状态 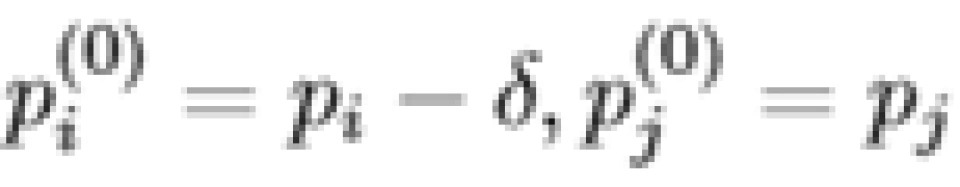
 ,根据之前的推导,把 δ 分配到信道 j 比分配给信道 i 能获取 更多的信道容量。重新分配后
,根据之前的推导,把 δ 分配到信道 j 比分配给信道 i 能获取 更多的信道容量。重新分配后 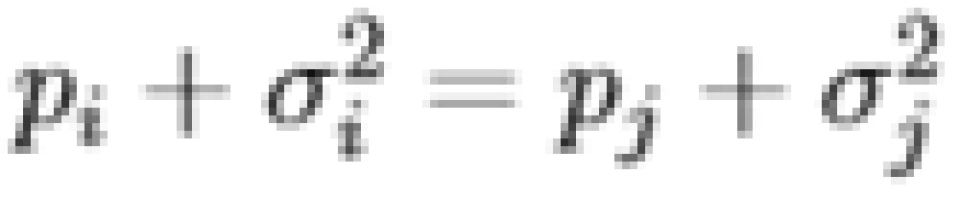
 或 pi = 0(此时
或 pi = 0(此时 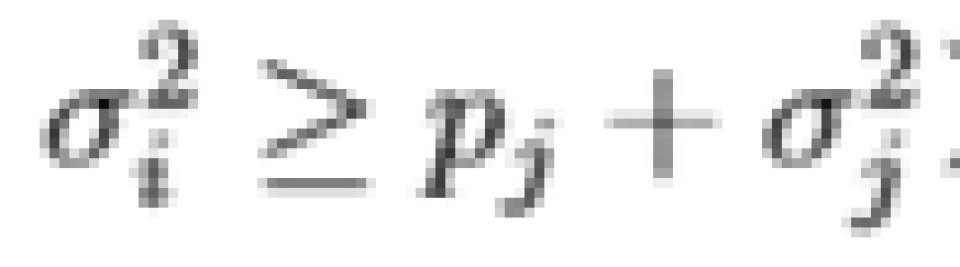
 )。
)。
3、 一个严谨的证明
我们重写 (1.1) 为
(3.1)
−ln(·)是一个凸(convex)函数,即目标函数是一个凸函数,同样的,也不难证明可行域 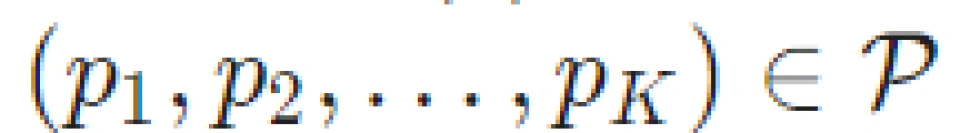 <span style=”color: rgb(31, 31, 31); font-family: –apple-system, BlinkMacSystemFont, ” segoe=”” ui”,=”” roboto,=”” oxygen,=”” ubuntu,=”” cantarell,=”” “fira=”” sans”,=”” “droid=”” “helvetica=”” neue”,=”” arial,=”” sans-serif;=”” background-color:=”” rgb(255,=”” 255,=”” 255);”=””>是凸的。即该优化问题是一个凸优化问题,拉格朗日函数为:
<span style=”color: rgb(31, 31, 31); font-family: –apple-system, BlinkMacSystemFont, ” segoe=”” ui”,=”” roboto,=”” oxygen,=”” ubuntu,=”” cantarell,=”” “fira=”” sans”,=”” “droid=”” “helvetica=”” neue”,=”” arial,=”” sans-serif;=”” background-color:=”” rgb(255,=”” 255,=”” 255);”=””>是凸的。即该优化问题是一个凸优化问题,拉格朗日函数为:
(3.2)
其 KKT 条件为
式 (3.3a) 可以重写为
(3.4)
如果
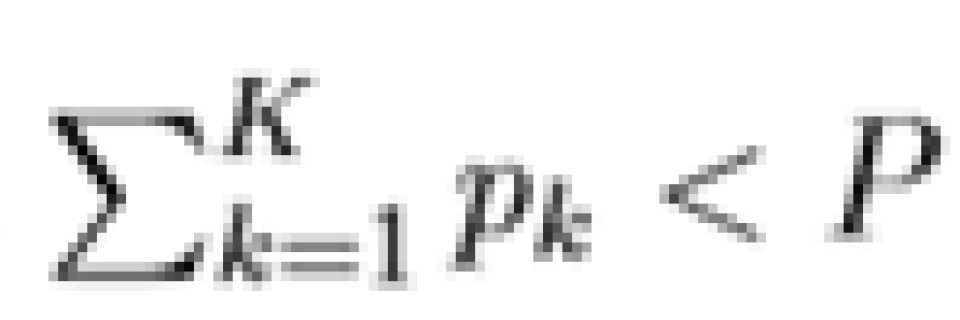 ,则
,则 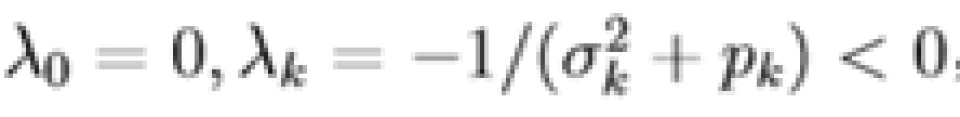 ,与 (3.3b) 矛盾。故
,与 (3.3b) 矛盾。故
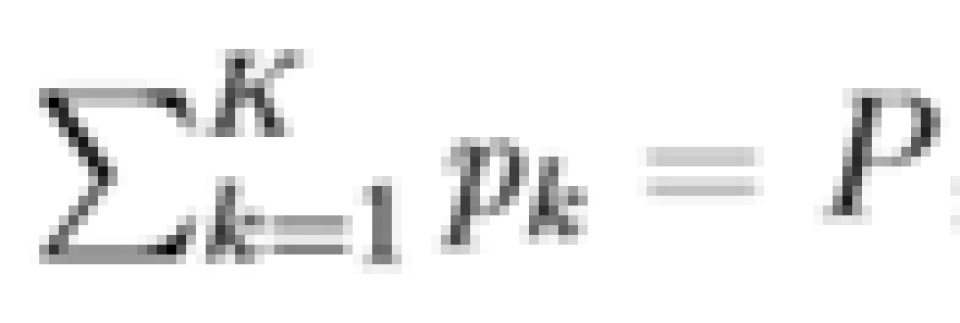 ,由
,由 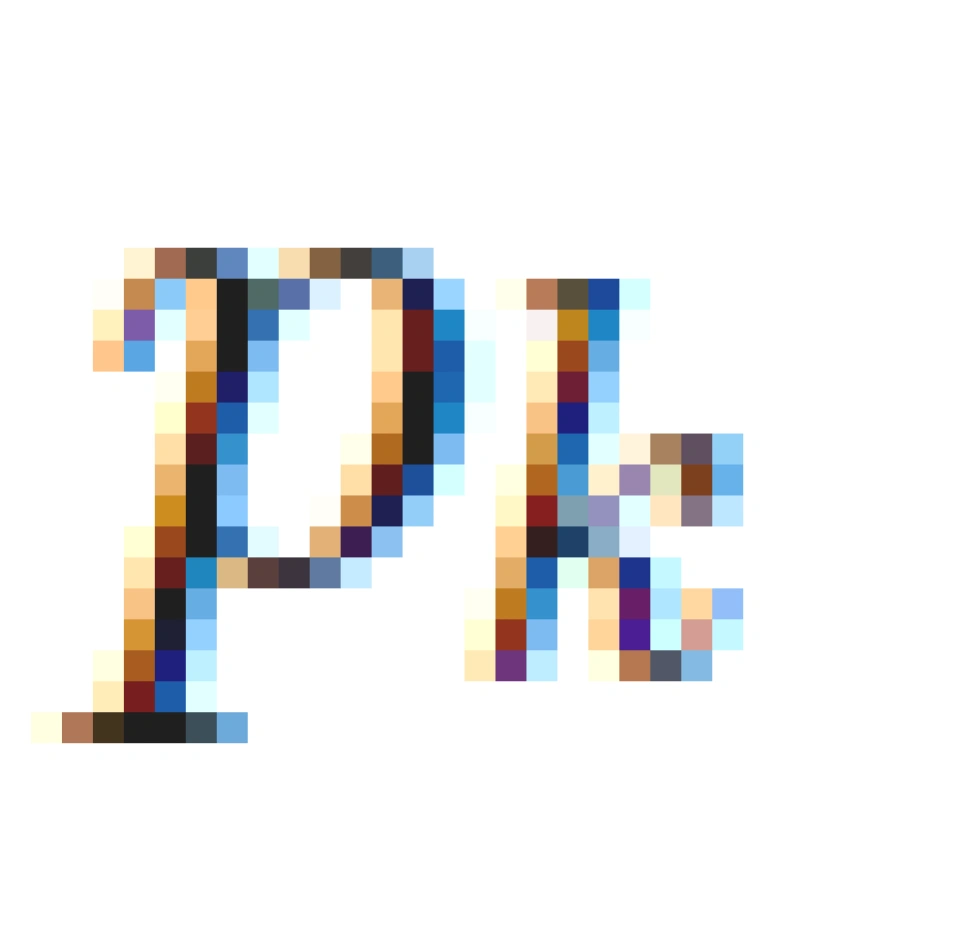 非负性可知
非负性可知  不全为零。
不全为零。
不妨假设 
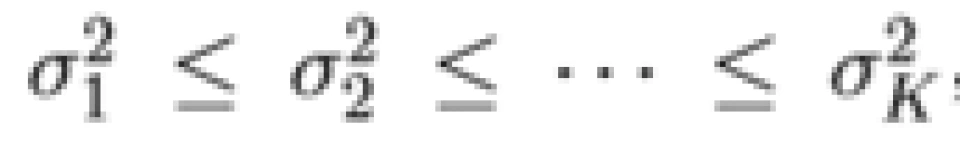 ,因为
,因为  不可能全为零,对应的
不可能全为零,对应的  为零,对于这些
为零,对于这些 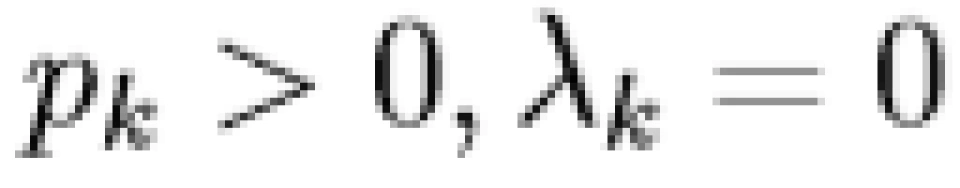 的信道:
的信道:
(3.5)
(3.6)
(3.7)
即上文所提到的,对于好的信道(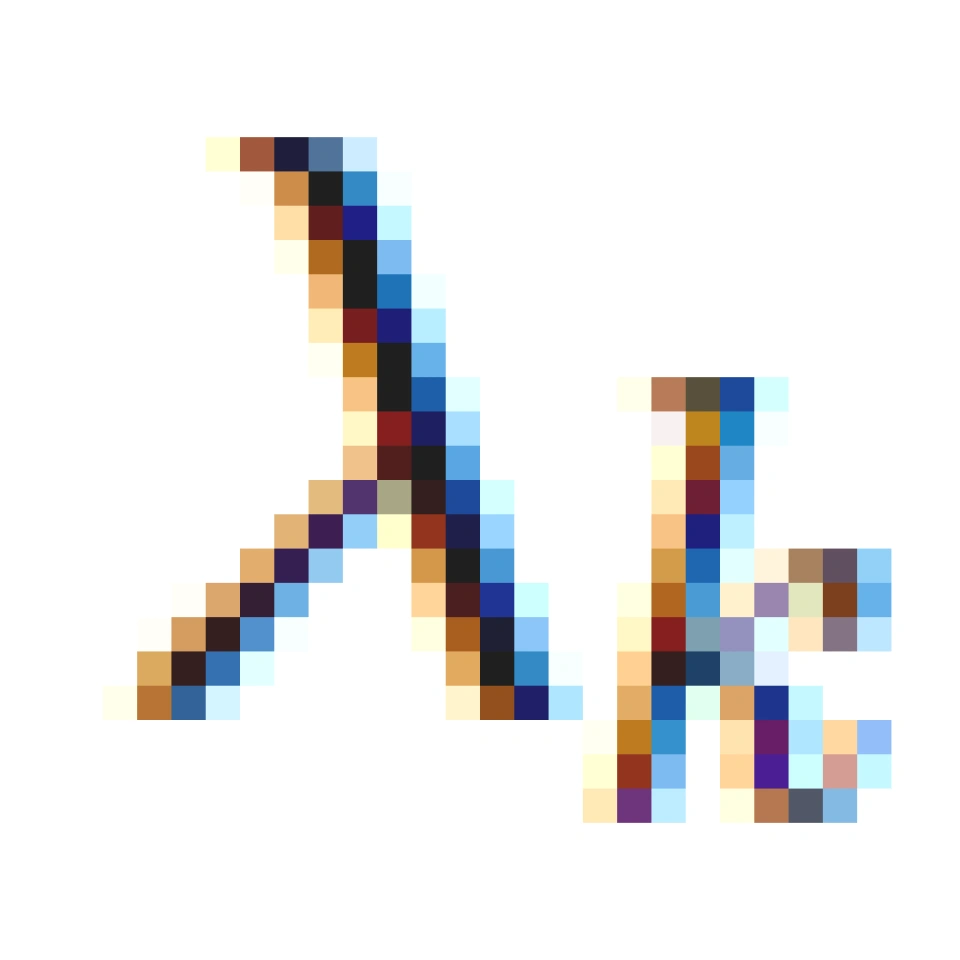 = 0),分配功率
= 0),分配功率 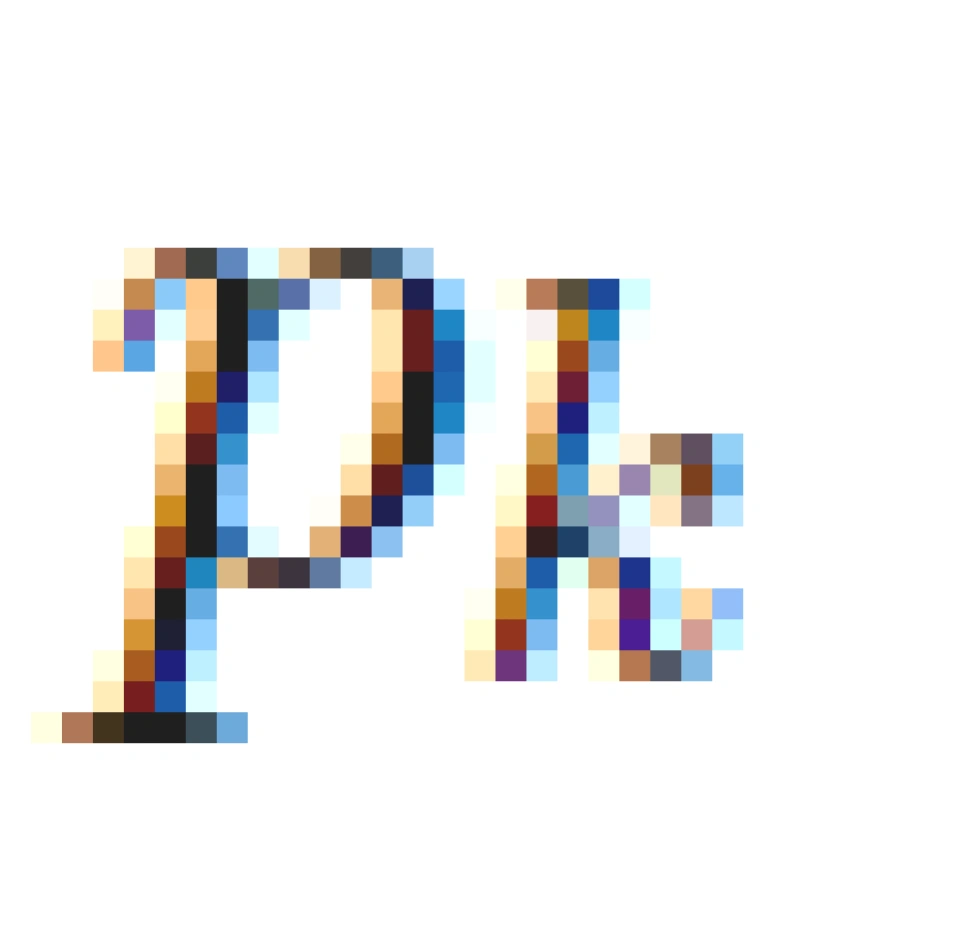 满足
满足 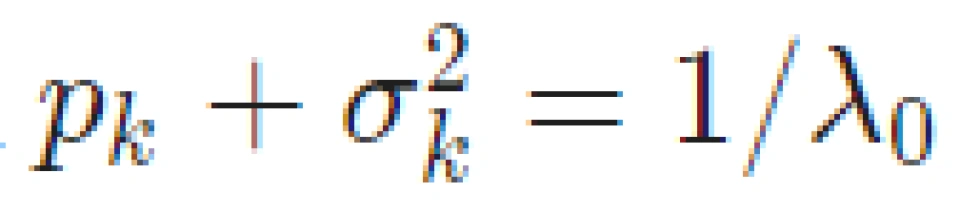 为定值,对于差的信道(
为定值,对于差的信道(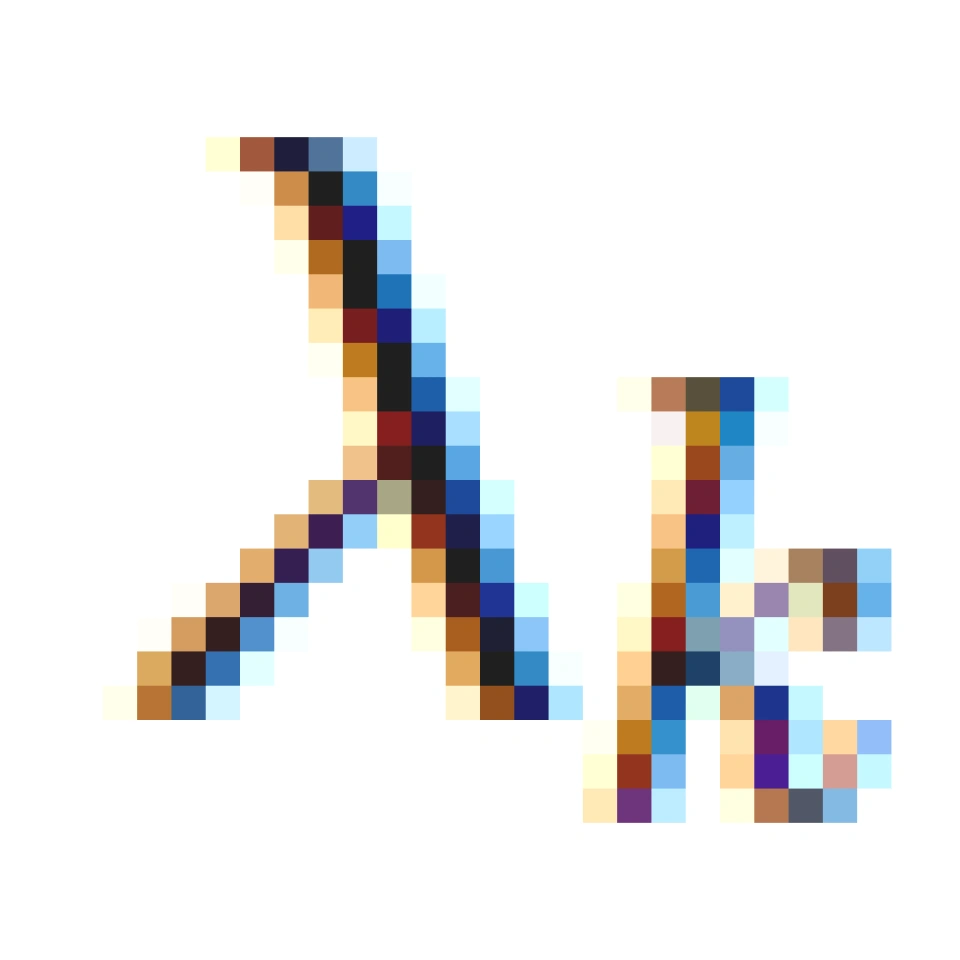 > 0,应当注意的是(3.7)指出,如果噪声功率为
> 0,应当注意的是(3.7)指出,如果噪声功率为 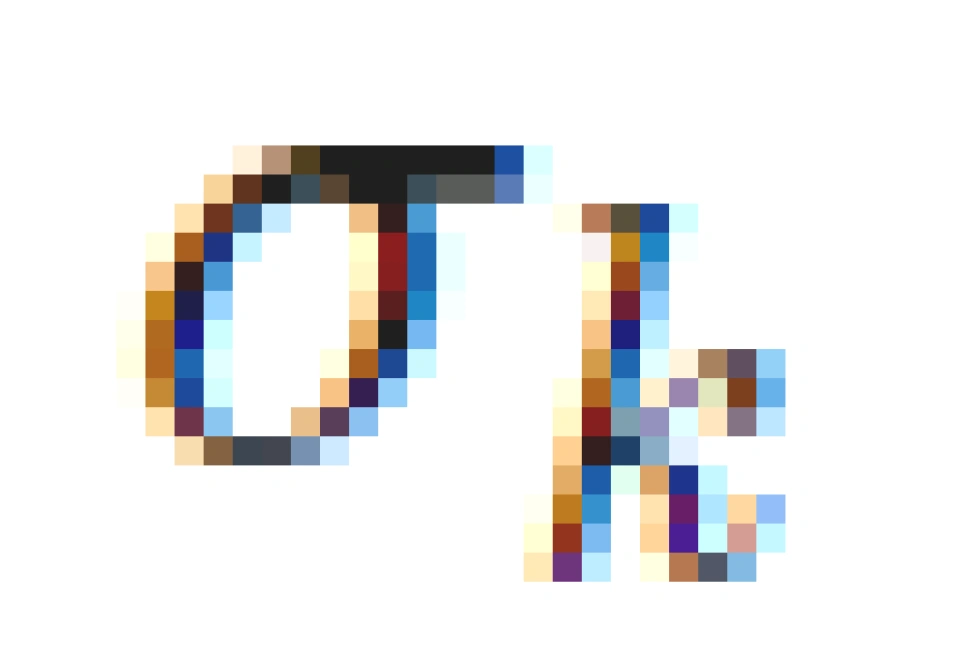 的信道是差信道,则噪声功率更大的信道也是差信道),则不分配功率,直到功率分配尽为止。
的信道是差信道,则噪声功率更大的信道也是差信道),则不分配功率,直到功率分配尽为止。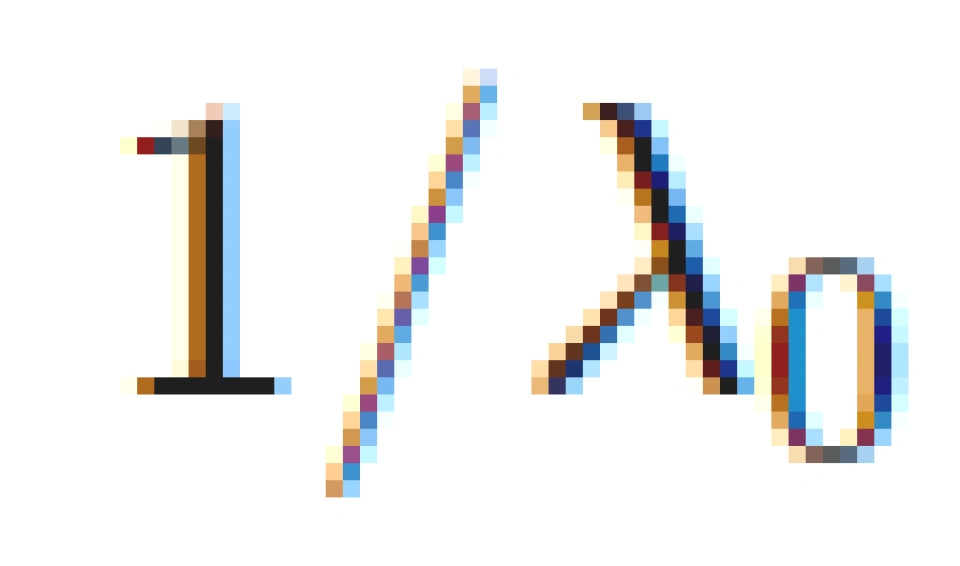 即上文的 p⋆。
即上文的 p⋆。
4、连续并联信道的注水定理
对于某一变换域(如频域上)的有色噪声 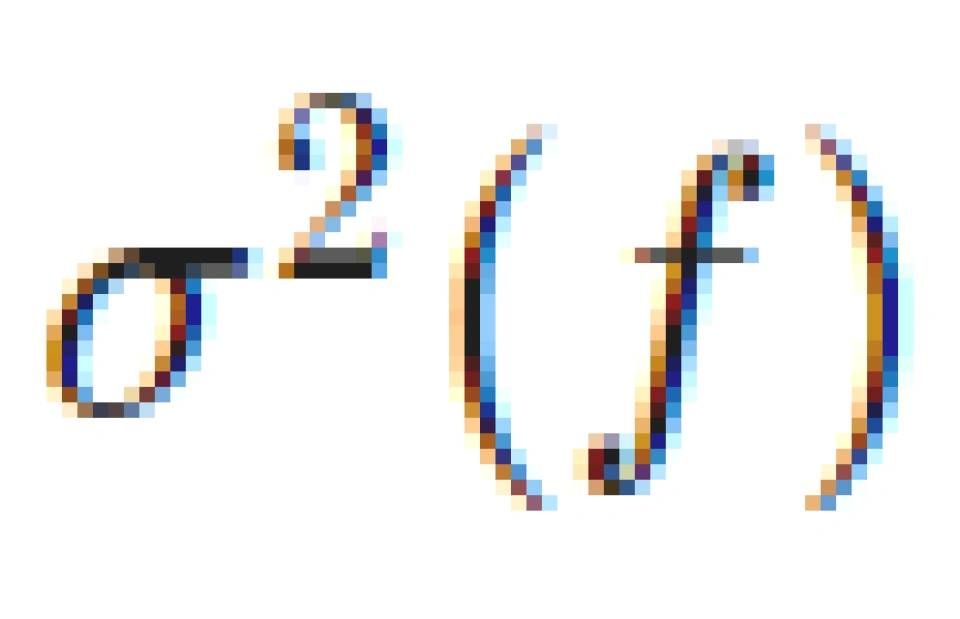 ,注水问题的优化可以写作:
,注水问题的优化可以写作:
(4.1)
构造拉格朗日泛函:
(4.2)
其 KKT 条件为:
上式中 δp(f) 是 p(f) 的变分。
当 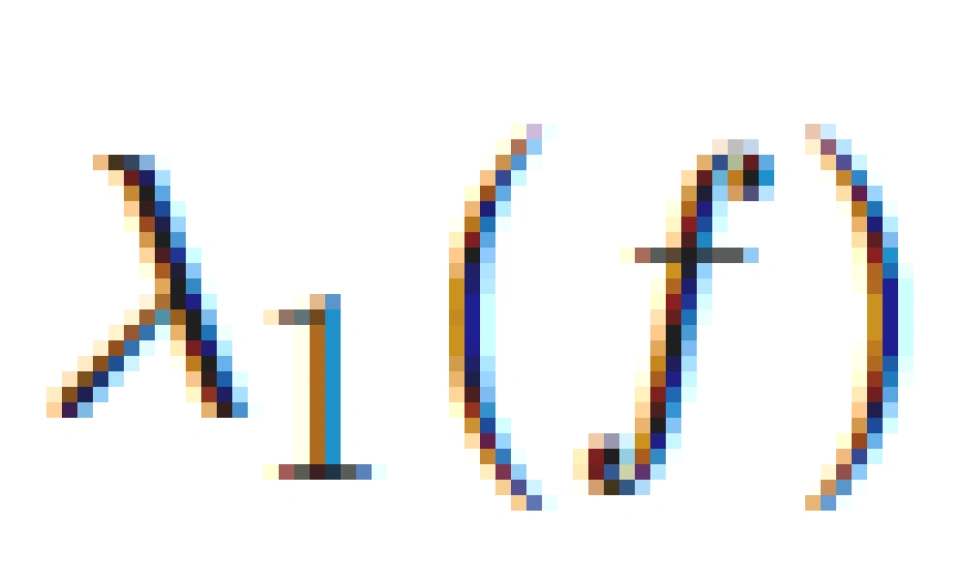 > 0 时(类似于前文的“差信道”), p(f) ≡ 0,进而有 δp(f) = 0。反之当 p(f) > 0 时,
> 0 时(类似于前文的“差信道”), p(f) ≡ 0,进而有 δp(f) = 0。反之当 p(f) > 0 时,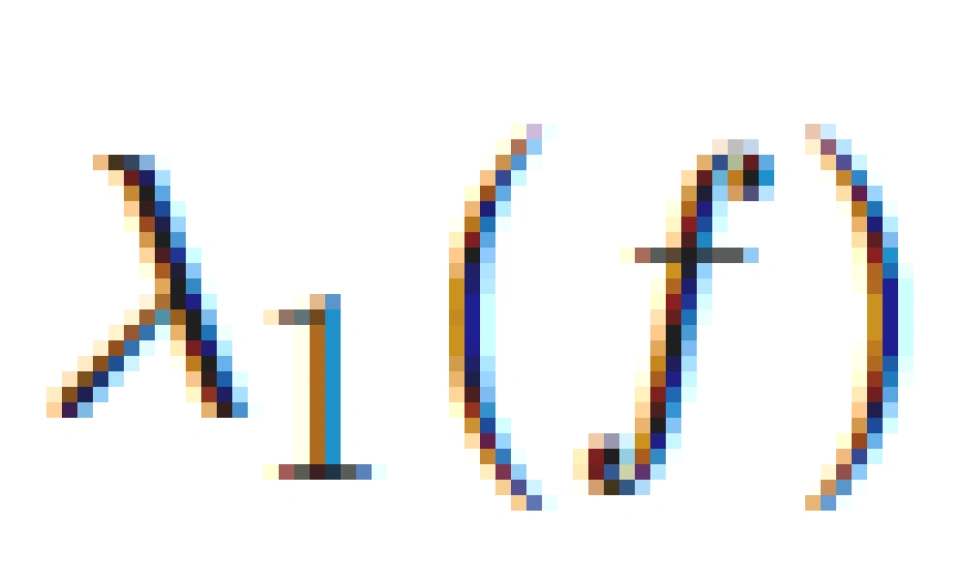 ≡ 0(类似于前文的“好信道”),此时
≡ 0(类似于前文的“好信道”),此时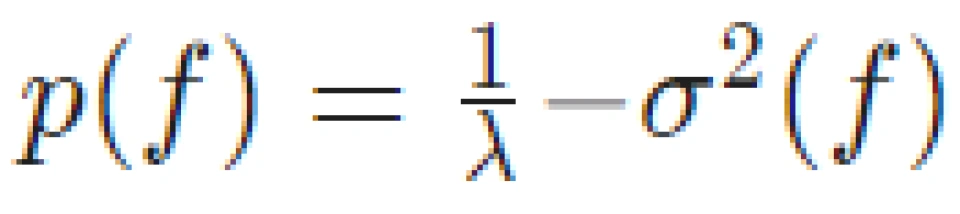 。综上:
。综上:
(4.4)
其中 p⋆ 满足
(4.5)
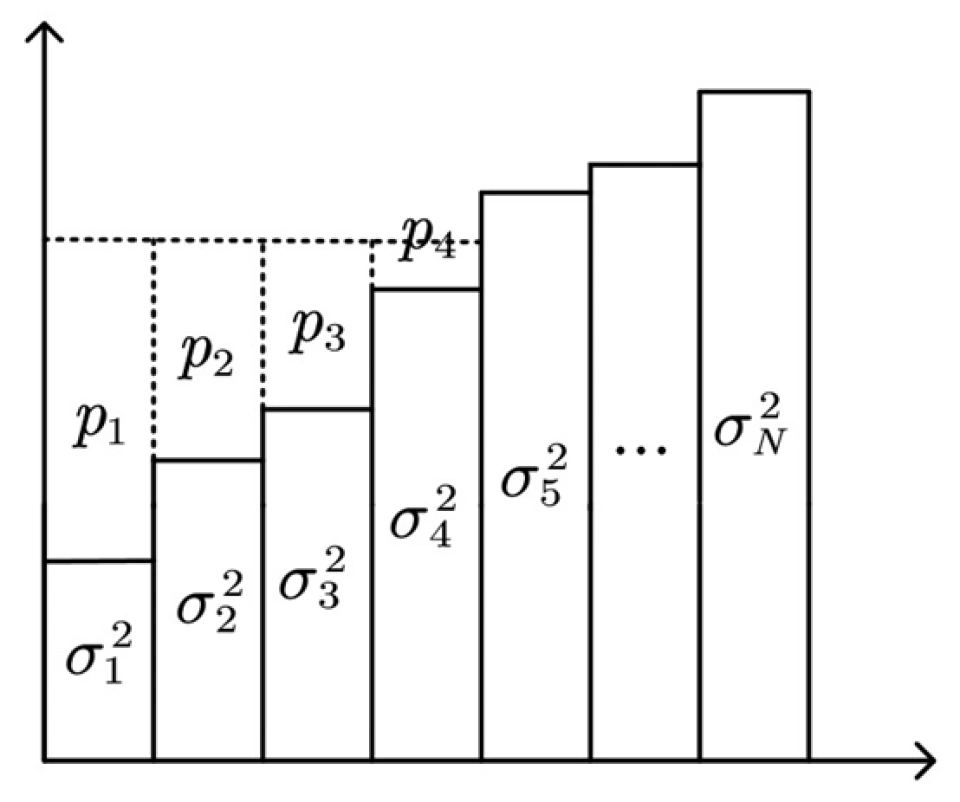
说了半天为什么叫注水?就是说把 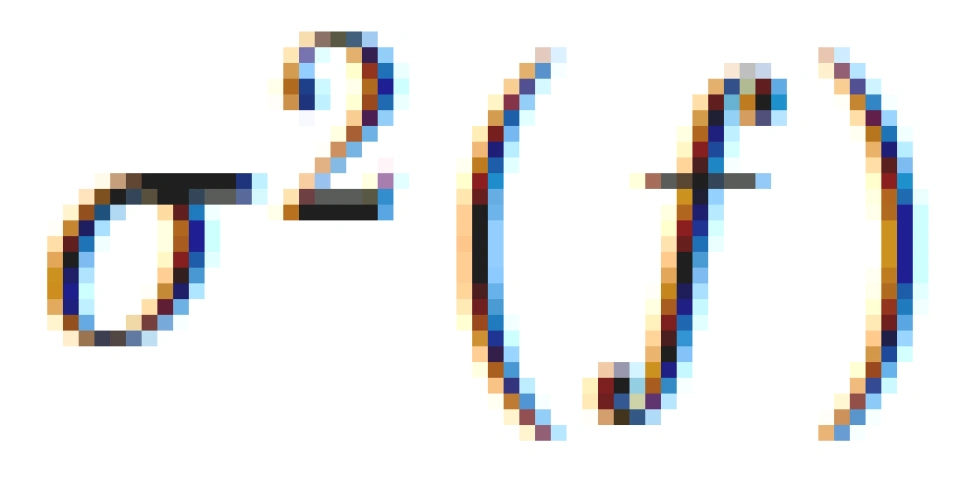 当作碗,功率是水往里倒,分配功率的地方,噪声功率加信号共功率(水平面)是平的,高出水面的噪声说明信道很差,不予分配功率。
当作碗,功率是水往里倒,分配功率的地方,噪声功率加信号共功率(水平面)是平的,高出水面的噪声说明信道很差,不予分配功率。

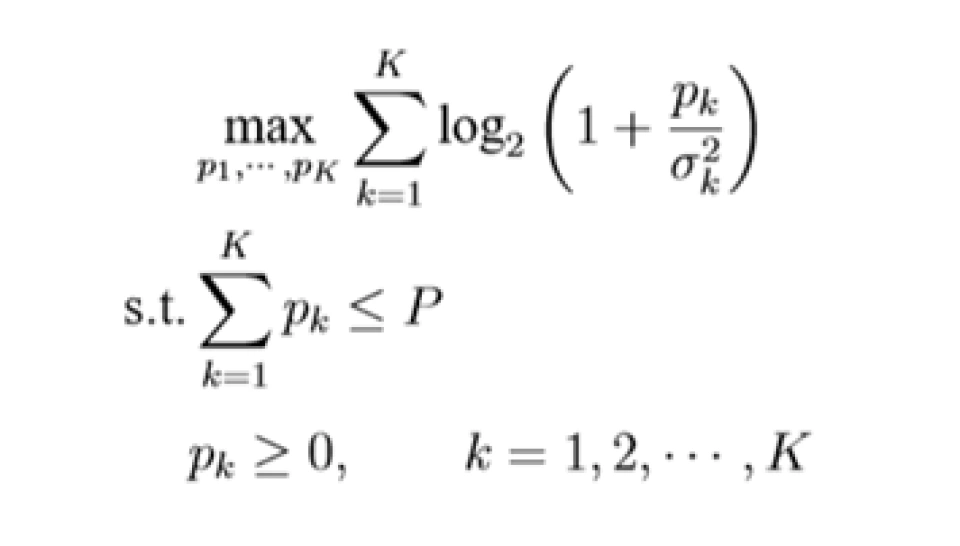
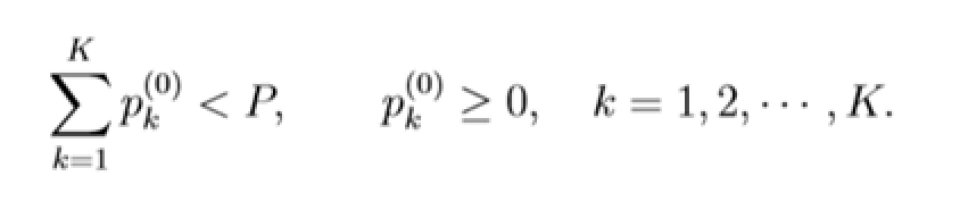
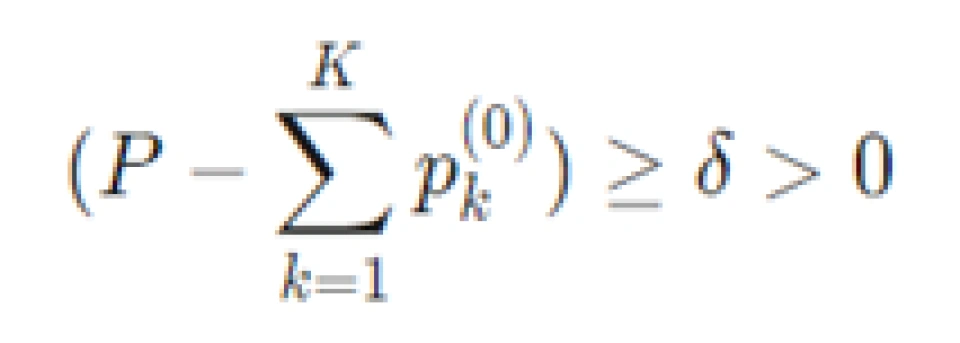
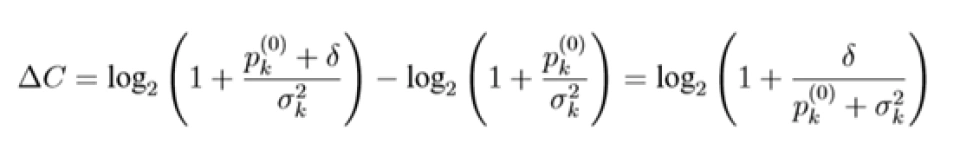
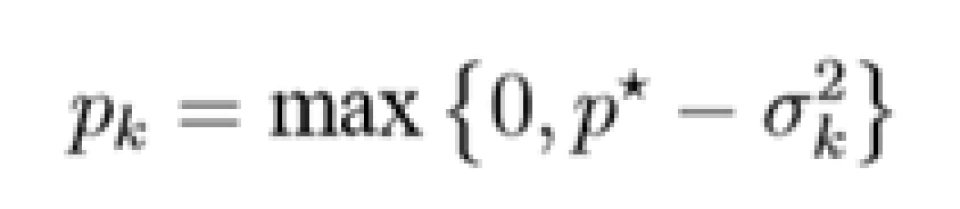
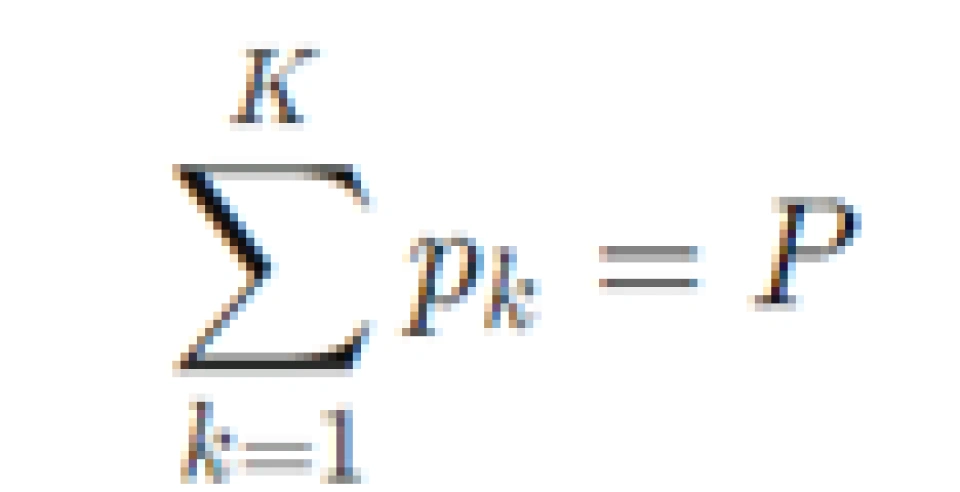
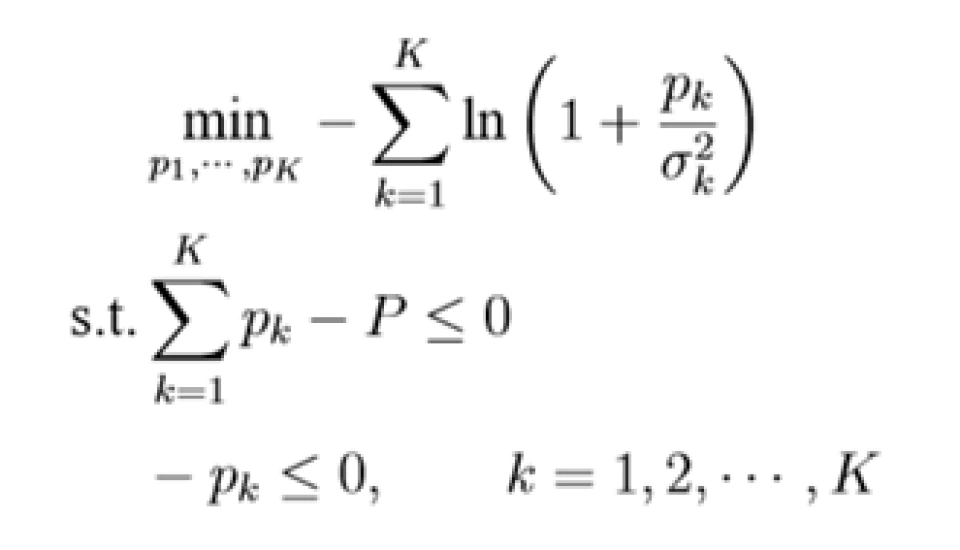
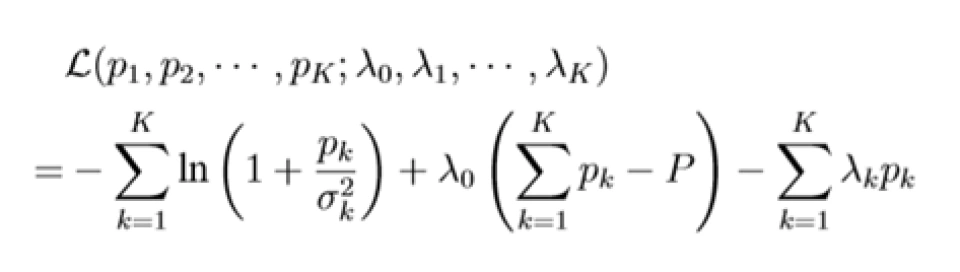
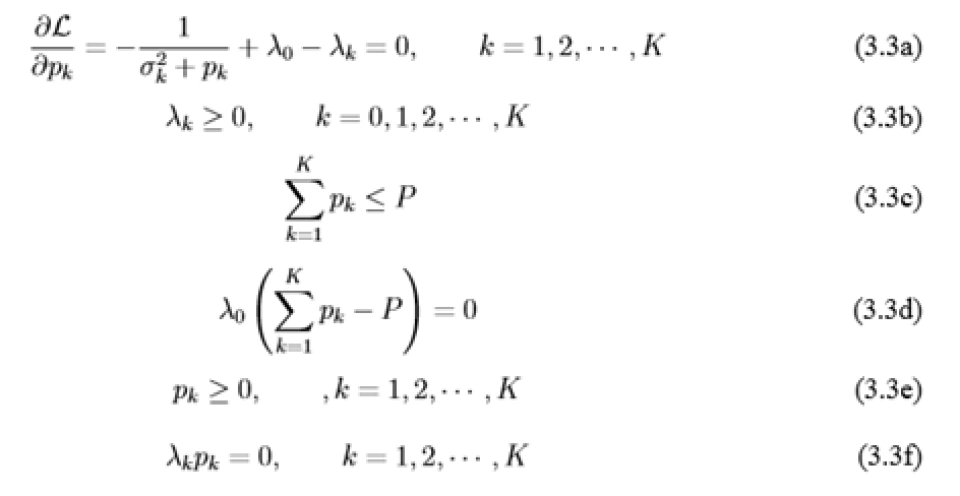
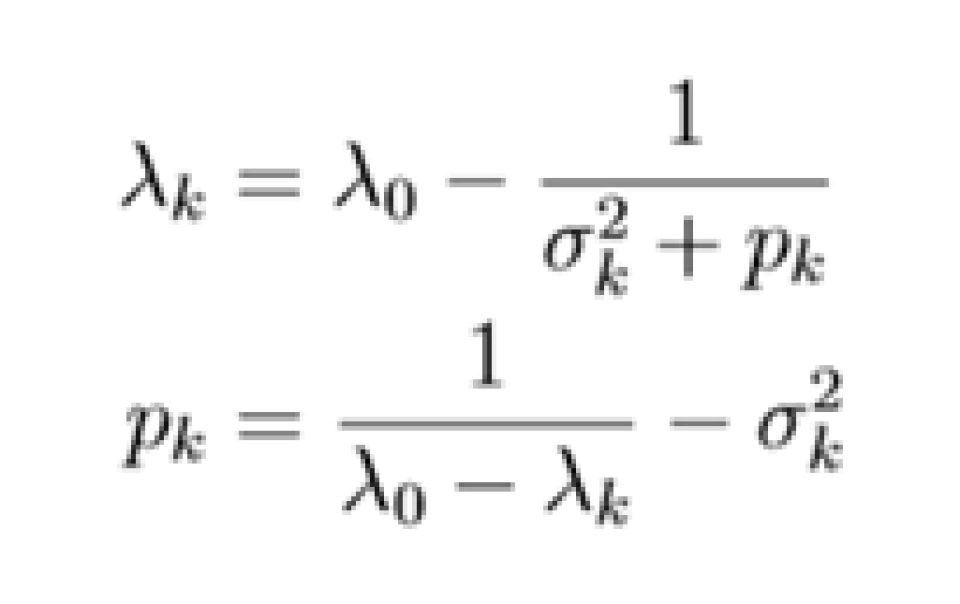
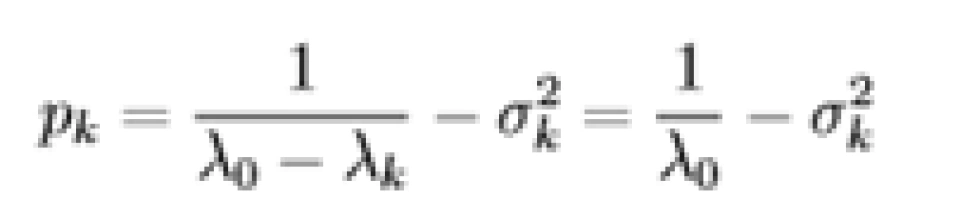
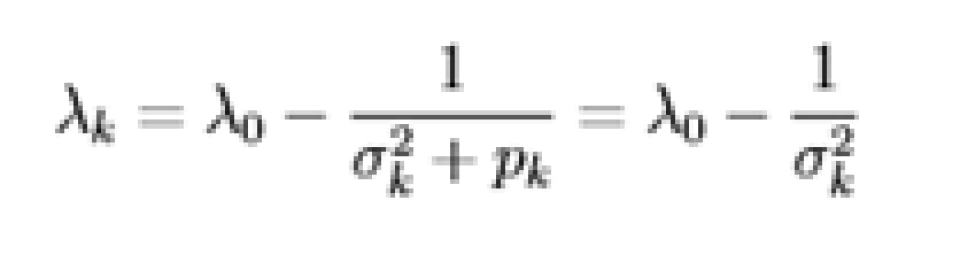
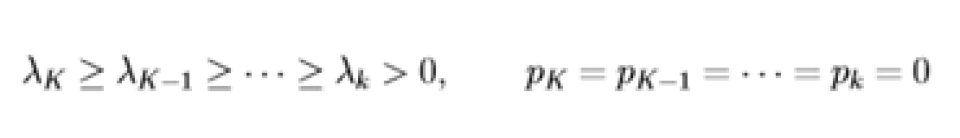
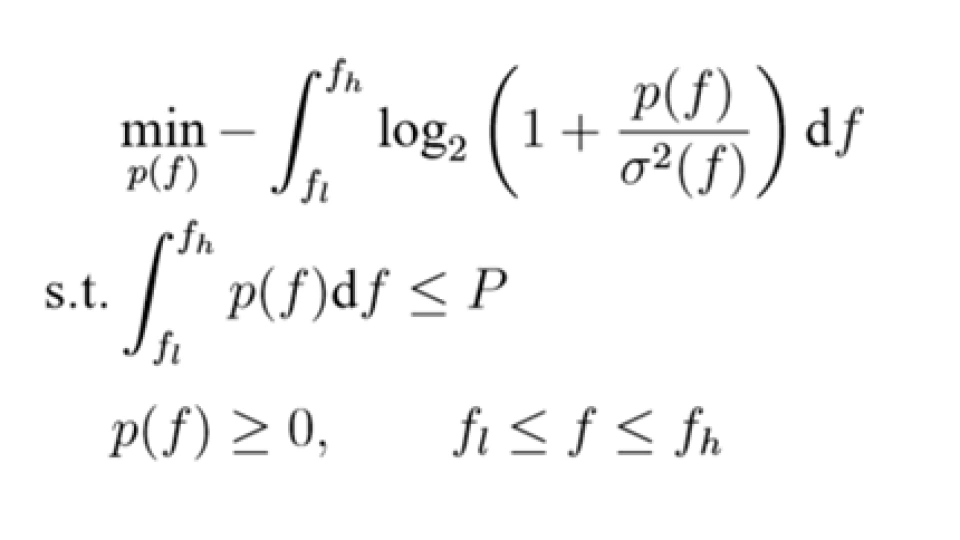
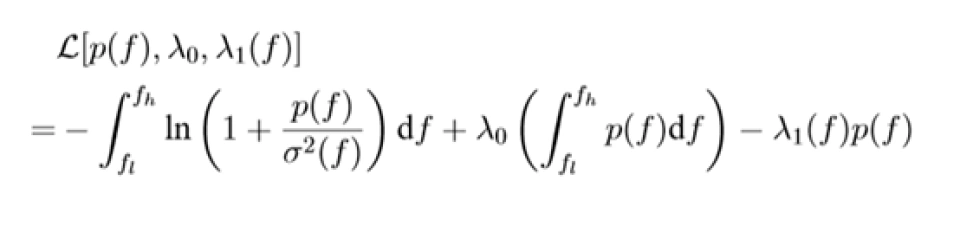
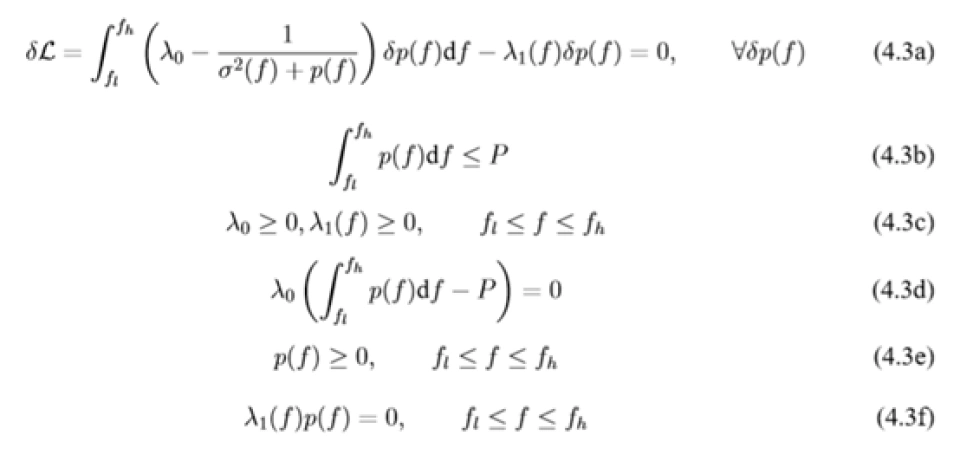
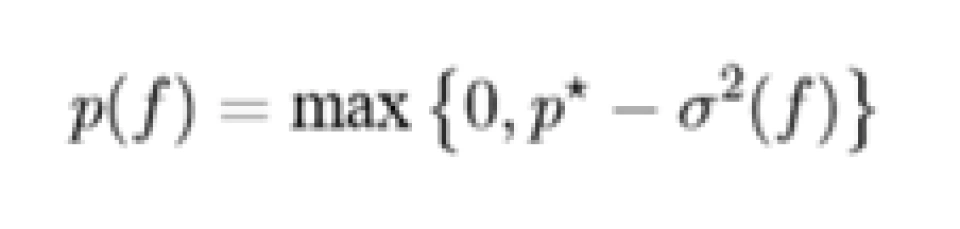


![[s-70]](https://www.bokeyuan.net/pic/image/emoji/cas/70.png)











