摘要:本文着重介绍航天工程中应用的天体力学,如:拉格朗日点,引力弹弓效应。联系嫦娥探月工程,旅行者号,以及对天体力学在航天中应用的一些设想。
引言:2018年5月21日,中国首颗、也是世界首颗地球轨道外专用中继通讯卫星发射升空。根据设计,“鹊桥”卫星在地月三体系统平衡点L2做拟周期运动,为着陆器提供中继服务。拉格朗日点是天体力学中限制性三体问题的五个特解,此概念在现代航天工程中有着广泛的应用。
天体力学的其他内容也在其他航天计划中有着重要的作用。旅行者号探测器是NASA建造的,探索太阳系外围空间的探测器,旅行者2号和旅行者1号分别于1977年8月20日和9月5日发射升空。它们巧妙地利用巨行星的引力作用,使它们适时改变轨道。这些航天计划的实现离不开对轨道的精妙设计,即对天体力学的巧妙运用。
正文:
一、“鹊桥”与拉格拉格朗日点
在“鹊桥”卫星的轨道设计中,运用了拉格朗日点这个天体力学概念。拉格朗日点,一个小物体在两个大天体的引力作用下,小物体相对于两大天体基本保持静止的点。这些点的存在由瑞士数学家欧拉于1767年推算出前三个,法国数学家拉格朗日于1772年推导证明剩下两个。
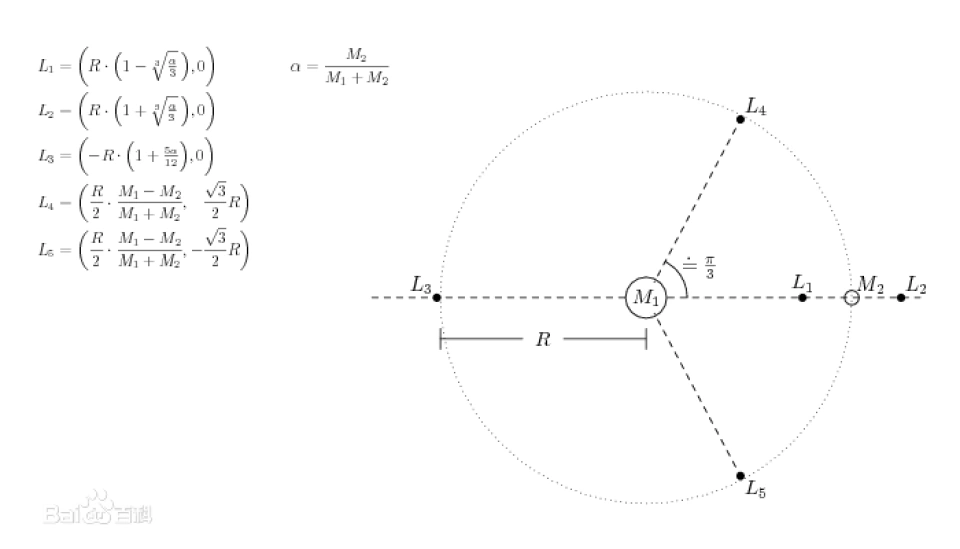
拉格朗日点有五个,假设两个大天体绕彼此做匀速圆周运动,L1,L2,L3在两个大天体所确定的直线上,L1在两个大天体之间,L2在两个大天体中较小的那个的轨道外侧,L3在较小天体关于大天体对称的另一侧,比地球距太阳略微远一些。地球与太阳的合拉力再次使物体的运行轨道周期与地球相等。L4,L5分别在以两天体连线为底的等边三角形的第三个顶点上,且在较小天体围绕较大天体运行轨道的前方,后方,与较小天体提前,落后60°。
结合图片一一介绍拉格朗日点的位置:
“鹊桥”正是处于L2上,但是L2不是一个稳定的拉格朗日点,在质点偏移L2时,质点无法稳点在L2附近。因此,航天器若想停留在L2,需要消耗一些燃料。
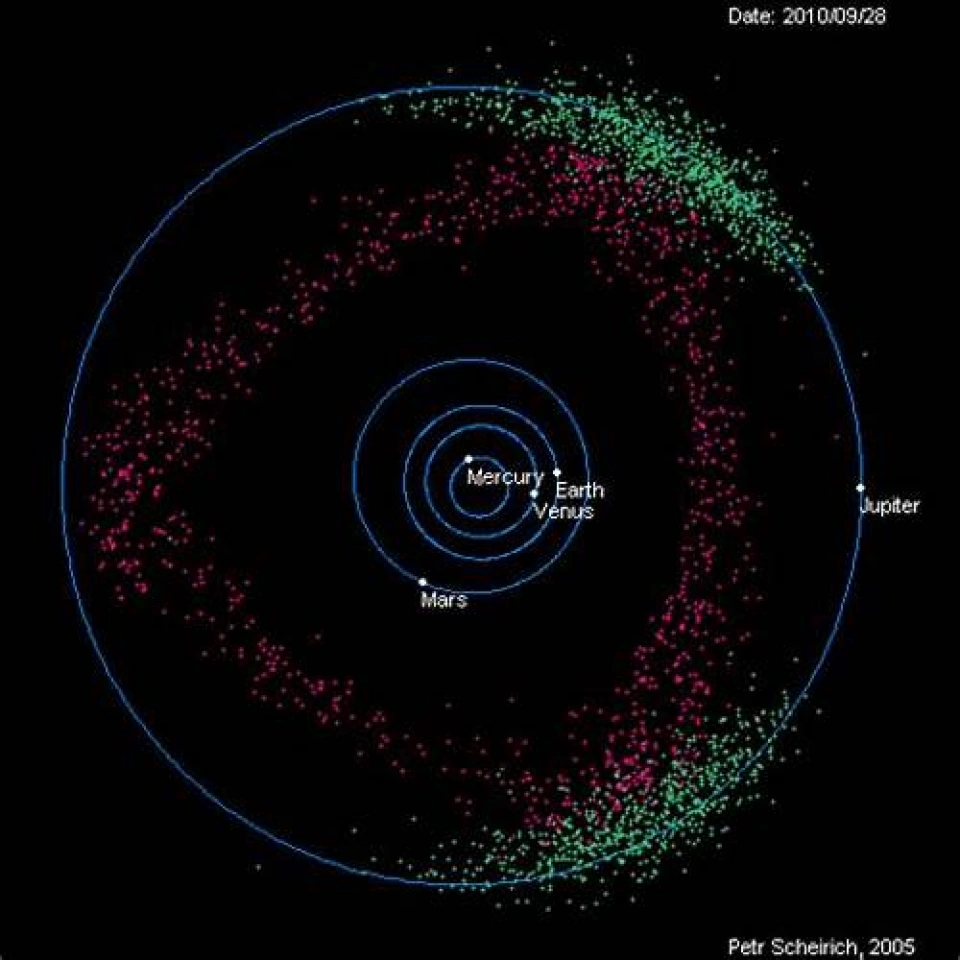
而L4,L5为稳定的拉格朗日点,当质点偏离L4,L5时,质点仍可稳定在L4,L5附近。自然天体中就有大量的实例,例如:1906年发现的木星的L4,L5的附近存在两个小行星群,称之为特洛伊群。
拉格朗日点处质点所受两天体的引力的合力提供向心力,质点角速度与两天体互相围绕转动的角速度相同。L4,L5为稳定拉格朗日点,有很多有趣的性质,以下着重介绍:
较小天体的质量m,较大天体的质量M.航天器质量m’,受M引力F1,受m引力F2.求证:m’在L4(L5)受到的合力指向M,m的共同质心:
1.如图所示,M,m,m’组成等边三角形,C为合力所在直线与M,m连线的交点,∠Mm’C=α,在力的合成平行四边形中,F合 与F2的夹角为β,可知α+β=π/3.
由正弦定理:
F1/sinβ=F2/sinα.F1/F2=sinβ/sinα.
F1/F2=M/m=sinβ/sinα.
2. 求质心位置,M到质心距离Xc=(M·0+mr)/(M+m)=mr/(m+M).
现设较大天体M处于A,较小天体m处于B;M和m组成的系统的质心处于C,拉格朗日点L,∠ALC=α’,∠BLC=β’,∠BCL=θ.
三角形ACL中:Xc/sinα’=AL/sin(π-θ).
三角形BCL中:(r-Xc)/sinβ’=BL/sinθ.
由以上两式得:Xc/(r-Xc)=sinα’/sinβ’.
r-Xc=Mr/(m+M). M/m=sinβ’/sinα’.
由此可得,α=α’;β=β’.
所以,合力指向M和m系统质心C.
日-地系统的L4,L5处远离地球的无线电干扰,可以设想在L4,L5处,安放空间射电望远镜、太阳望远镜等航天器。
二、旅行者号与引力弹弓效应
旅行者号探测器利用引力弹弓效应提高速度大小改变速度方向,以此适时改变轨道,达到太阳引力场的逃逸速度。
轨道交会是指2个运行在不同轨道上的航天器在空间某点彼此接近的过程。当航天器与一天体交会后,获得了比交会前更大的速度的效应,称为引力弹弓效应。
在这个过程中,天体与航天器组成的系统机械能守恒,动量守恒。设天体质量M,航天器质量m,M>>m.在相对于天体静止的参考系中,航天器是以一个双曲线轨迹靠近之后远离的。
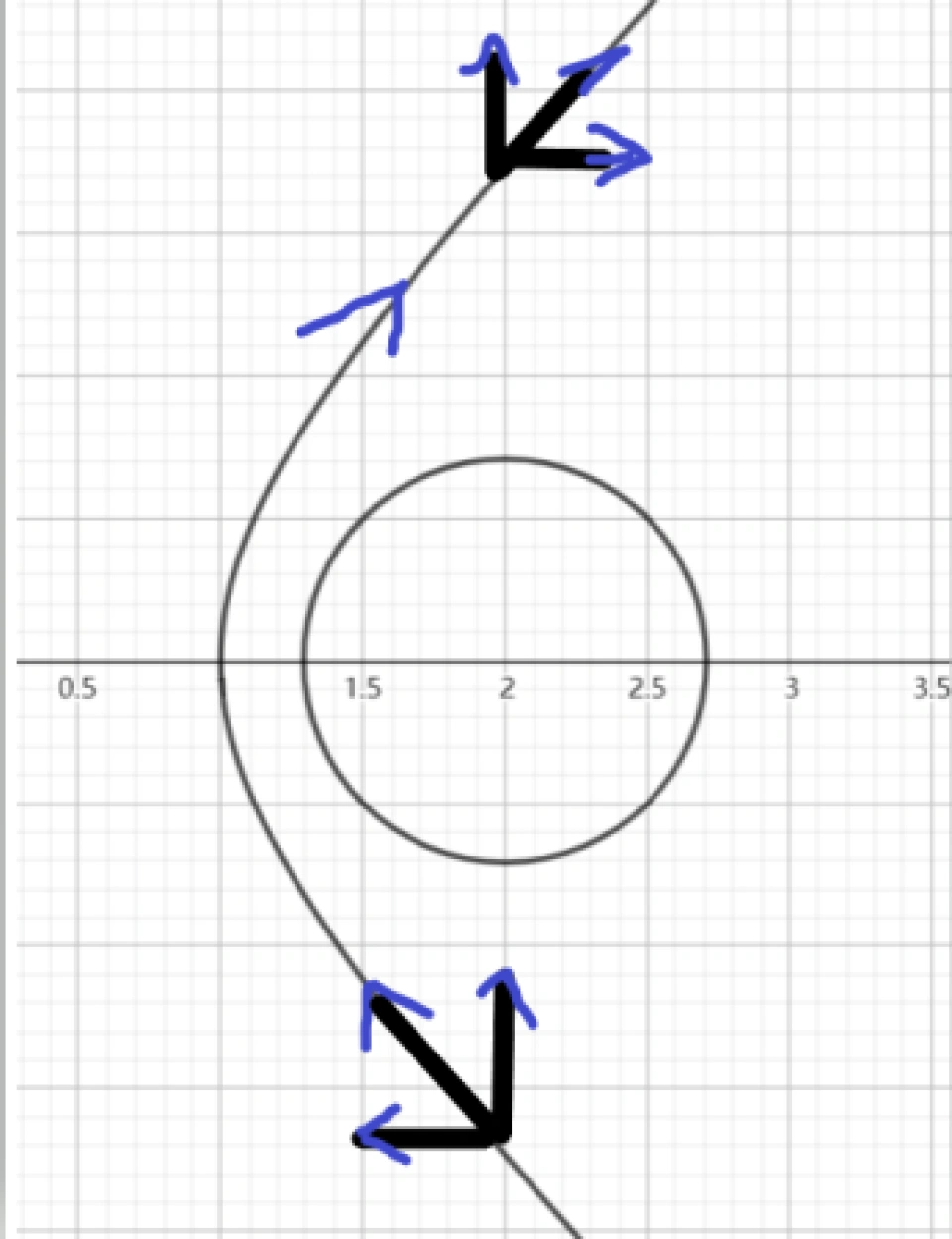
图中圆表示天体,双曲线表示相对于天体静止的参考系中航天器的轨迹。航天器离开天体时和靠近天体时,在航天器与天体距离相同处,速度大小相同。在图中,垂直于双曲线对称轴的速度分量v1在关于对称轴对称的两点处不变,平行于对称轴速度分量v2反向。
现在假设天体在一轨道上运动,选择相对于该天体环绕的中心天体静止的参考系,在图中表示为向右运动速度为V,在这个参考系中,航天器在天体轨道切线(即图中x轴)方向速度叠加上了天体的轨道速度,靠近时为V-v2,远离时为V+v2;在垂直天体轨道切线方向的速度不变。由此,航天器与天体交会后,获得了比交会前更大的速度,这就是引力弹弓效应。
可以先约掉等式两边航天器垂直天体轨道切线方向的速度带来的航天器动能,把这个过程视作完全弹性碰撞。
m<<M时,v2’=V+v2 ; V’=V.
与前面的讨论结果一致。
引力弹弓效应为远距离太空旅行的提速和变轨提供了一种节省燃料的方式,在行星探测方面有广泛的应用。这个物理过程是可逆的,由此,我们也可以运用此效应减速,以此发射航天器探测太阳,水星等地球轨道内侧的天体。
结论:天体力学在航天工程技术中有着广泛的运用,为轨道的设计提供依据。使人类飞向太空的步伐走得更稳,更远。航天计划的实现离不开对轨道的精妙设计,即对天体力学的巧妙运用。



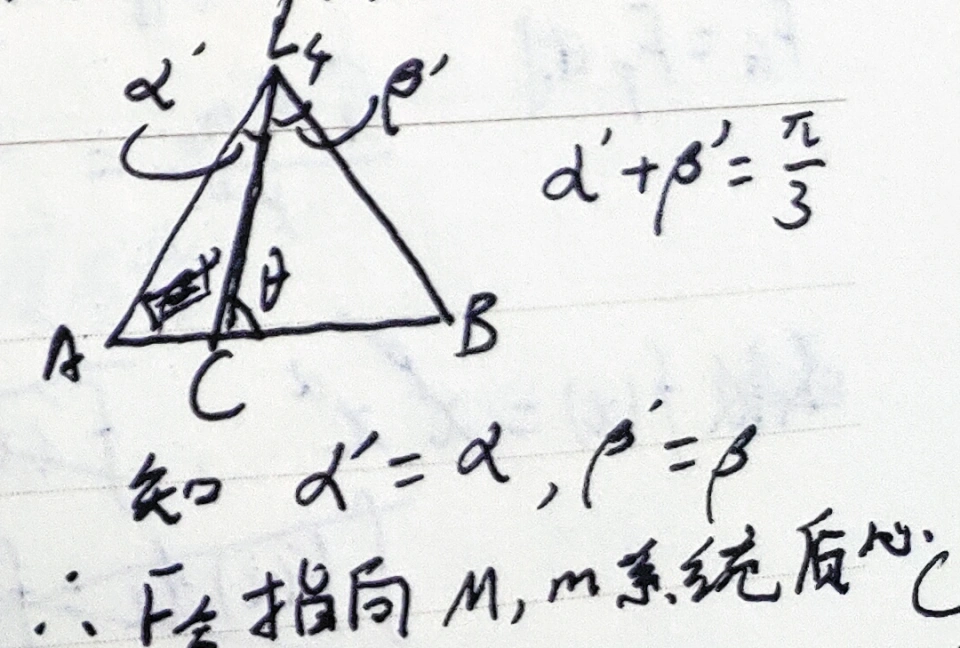
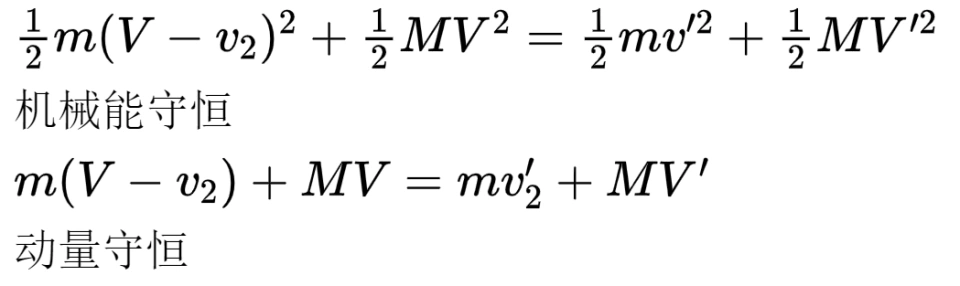
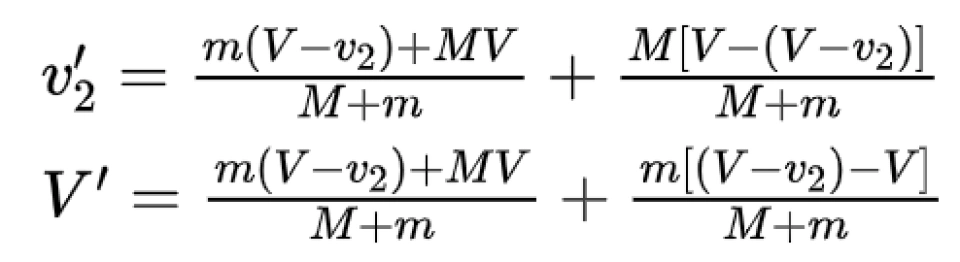

![[s-70]](https://www.bokeyuan.net/pic/image/emoji/cas/70.png)












