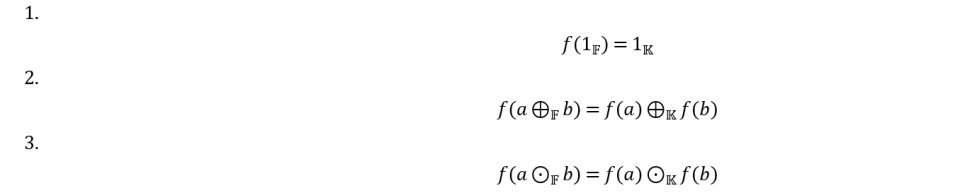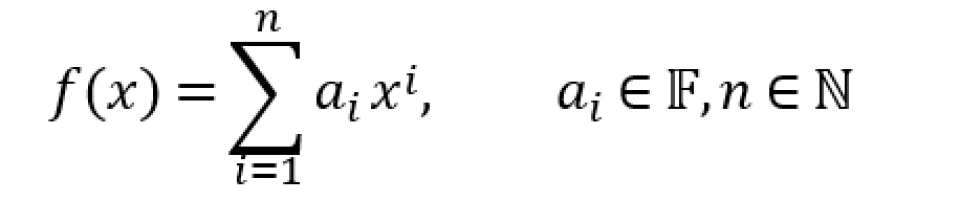科普驿站 第八十二期
科目:数学
难度:B1
讲师:萌萌哒小西瓜
第四部分:代数数
上一个部分中,我们已经完成了有理数的构造,现在我们沿着古人的路线(也是课本的路线),试着去得到实数——我们这个故事的终点。
从公元前五百年,毕达哥拉斯的得意门生希帕索斯第一次提出了√2是不是有理数开始,到19世纪末戴德金分割最后完整地定义了实数,前后两千余年波澜壮阔的历史,代数、几何、分析将轮番上场,一个个辉煌的名字将在这片舞台上依次出现,对数字的研究曾经是推动整个数学前行的巨大推手——而事实上直至今天,还有许许多多的问题没有解决。
别急,我们的好戏才刚刚开场。
希帕索斯的构造——第一个无理数
a^2+b^2=c^2
于是人们开始了研究二次方程的历程
x^2=a
很快,希帕索斯提出了一个重要的结论——x^2=2在有理数域上没有根。证明如下(这是一个神奇的证明,在每一本初中课本上都有,但更让人震惊的是居然很多人不会证,以至于这个经典的题目甚至能有资格在2017年上海交通大学的自主招生考试中,当时让我着实震惊许久):
设x^2=2,假设x是有理数,则有最简整数比
x=p/q, (p,q)=1
那么
x^2=p^2/q^2 =2
于是
2|p
那么
4|p^2
所以必然
2|q
矛盾。
当年的人类只发现了有理数,这无疑是晴天霹雳。如果我们想要给每条线段都定义一个长度,那么两条直角边为1的三角形斜边肯定是一个数字——但这个数字不是有理数!最终,毕达哥拉斯的追随者们没有解决问题,只能解决了提问题的人——把希帕索斯扔入了大海之中……
域的扩张
假设我有两个域F和K,存在这样一个单映射f:F→K满足:
我们称f为F和K之间的单同态。其实这说明了F应该是跟K里面的一部分是一样的(严格的话说,同构的),或者说,F可以看做是K的一部分。于是我们称域K为域F的扩张。
而域扩张里最简单的扩张就是单扩张——任取x∉F,如果K是F的域扩张中包含x的最小那个,称之为单扩张,记作K=F(x)。
例如啊,我们可以验证Q(√2)={a+b√2|a,b∈Q}是Q的一个单扩张(这里我们代数的定义√2是方程x^2=2的一个根——但我们不讨论这个根是几,就形式上假设有这么个根)。留作证明答案略,读者自证不难。给个小提示,首先根据加法和乘法的封闭性,Q(√2)肯定得包括{a+b√2|a,b∈Q},然后只要证明这是个域即可——只需要证明1/(a+b√2)也有x+y√2的形式即可。
同理,Q(∛2)={a+b∛2+c(∛2 )^2 |a,b,c∈Q}也是个单扩张。
这是一个有趣的话题,很多同学都会注意到形如a+b√2的东西关于加法和乘法是封闭的,并且挖掉0关于除法也封闭,但是很少有人能继续思考下去——但是Galois没有,他以此提出了整个抽象代数理论,一举解决化圆为方、三等分角、立方倍积、五次以上求根公式等上千年悬而未决的问题。
我们再做一个定义,α在F上代数,如果存在一个一元多项式
有f(α)=0,例如√2在Q上代数。
如果K的每个元素都在F上代数,则称K为F的代数扩张。
代数数域
在初中课本上,我们论证了√2是无理数(不是有理数),然后说,有理数和无理数共同组成了实数。现在有个问题,是不是所有无理数都是√2这样的形式呢——或者说,是不是实数R就是F的一个代数扩张呢?
很遗憾,不是的。如果我们把有理系数多项式的根(或者说整系数多项式的根)放在一起,构成的是代数数域,是复数域的子域,但和实数域并没有直接关系。(这里其实遗留了两个问题,供同学们思考:为什么整系数多项式的根的和还是整系数多项式的根,为什么整系数多项式的积还是整系数多项式的根。)
例如,虚数i(i^2=-1)是代数数,但不是实数;e、π是实数,但不是代数数。前者是显然的,后者的证明就很复杂了——因为本身e和π就很复杂。在下面的文章中,我们将构建一个强大的理论,论证代数数比实数少——甚至,我们可以证明你随便选择一个实数,是代数数的概率严格为0。
一切退回原点——我们知道了有无理数的存在,但好像还是寸步难行?代数的办法已经帮了我们很多了,现在,伟大的Cauchy出现了,他将为我们带来新的观察。
【本文为耀星会作者的原创作品,未经允许,禁止盗用、转载、篡改文章,否则耀星会和作者将追究版权责任。】