科普驿站 第八十二期
科目:数学
难度:B1
讲师:萌萌哒小西瓜
第三部分:有理数(下)
上一篇文章中,我们利用自然数、依靠加法生成了整数加法的Abel群,去掉了0后依靠乘法生成了正有理数乘法的Abel群,现在我们把整个有理数都构造出来。
模仿上一篇文章,我们有两个思路生成有理数:
1.根据已有的整数,去掉0再依靠乘法生成非零有理数乘法Abel群,最后补充定义有理数加法。
2.根据已有的正有理数,补上0再依靠加法生成有理数加法Abel群,最后补充定义有理数乘法。
这两条思路都是行得通的,实际上小学、初中我们走的就是下面的二号线路,但在大学里我们更应该走一号路线,因为这符合抽象代数商域的想法。
我相信每个有能力,有毅力看到这里的同学都能自行按照上面两条路线完成有理数的构造,并且定义大于小于的关系,这里从略。我们介绍一些更高角度的问题。
域
上一篇文章我们介绍了一个代数结构——Abel群,要求五个(封闭性、结合律、单位元、逆元、交换律),在这里我们介绍一个更强的代数结构——域(Field)。
我们称(S,⊕,⊙)为域(Field),如果满足:
1.(S,⊕)是一个Abel群
2.(S-{0},⊙)是一个Abel群
3. 满足分配律,即(a⊕b)⊙c=(a⊙c)⊕(b⊙c)
显然,我们知道有理数关于加法和乘法构成域(Q,+,⋅)。事实上,实数和复数也分别构成域(R,+,⋅)和(C,+,⋅),但是整数(Z,+,⋅)不构成域(整数乘法不构成群)。
根据我们的构造,我们可以断言,有理数域是最小的数域(这是一个很重要的定理,严格的表述为任何一个特征为无穷的域都包含一个与有理数域同构的子域)。
序、有序域
还记得我们一开始说的吗?数学是研究结构的科学,研究三种结构:代数结构,序结构,拓扑结构。我们到现在主要是应用代数结构完成的有理数构建,但是也用到了一点序(大于小于)的理论。我们这里将之完整的呈现出来。
在集合S上定义二元关系R,实质上是S×S的子集。我们记aRb,如果(a,b)∈R。
如果二元关系≼满足下面的条件,我们称之为偏序:
1.自反性:对任意x,有x≼x。
2.反对称性:对任意x、y,如果x≼y且y≼x,则x=y。
3.传递性:如果x≼y且y≼z,那么x≼z。
显然,我们已有的大于等于、小于等于都是偏序关系。此外,整除也是偏序关系(对a,b∈N,如果a|b,即存在c∈N使得ac=b,则记a≼b,可以验证这也是偏序)。
对于偏序,去掉等号称为严格偏序,即a≺b当且仅当a≼b且a≠b,例如大于和小于。
特别地,如果对集合S中任意两个不同元素a、b,a≼b和b≼a总成立一个,称此偏序为全序。可以看到大于等于和小于等于都是全序,但是前面的整除关系就不是全序了。
在域(F,⊕,⊙)上,如果有严格偏序≺满足:
1.对任意a,b,c∈F,a≺b必然有a⊕c≺b⊕c 。
2. 对任意a,b∈F,如果a≺b,那么对任意c∈F满足0≺c,有ac≺bc 。我们称(F,⊕,⊙,≺)为有序域。
显然,(Q,+,⋅,<)是一个有序域,并且可以证明,任何一个有序域都包含一个同构于它的子域。这个定理的证明略微复杂,可以参考:https://zhuanlan.zhihu.com/p/39281734。
绝对值、距离
在继续往前探讨之前,我们已经可以解决一些中小学里已经出现过的问题了。
初中,我们定义过一个数字的绝对值:
如果有印象的话,初中那个时候我们是这么定义的:一个数在数轴上所对应的点到原点O的距离称为这个数的绝对值。实际上这个话的问题非常大,它至少没说清楚两个问题: 1. 什么是数轴? 2. 什么是距离?
我们先解决下面这个问题,什么是距离(distance)。
在大学里,对于一个集合X,我们称函数d:X×X→F(F为Q或R)为距离,如果满足:
1.正定性:d(x,y)≥0恒成立,且d(x,y)=0当且仅当x=y。
2.对称性:d(x,y)=d(y,x) 。
3. 三角不等式:d(x,z)≤d(x,y)+d(y,z)
这样,(X,d)就构成了一个距离空间(或称度量空间),这将产生很好的拓扑性质,整门泛函分析的起点也正基于此。
Wait a minute! 这个距离的定义好像……没有直接指明啊,也就是说,虽然我们通常意义下的距离
满足这个条件,但是似乎并不唯一?
没错,确实,还有其他距离。我们举一个例子:任选p为素数(素数是正有理数,且只能被1和自己整除),我们定义函数
f:Q→Q
对于x∈Q,假设x=(a/b)p^n,其中(a,p)=(b,p)=1,a,b,n∈Z,我们定义
f(x)=p^(-n)
然后定义
d_p (x,y)=f(x-y)
可以验证,这也是一个距离(称为p-adic距离)。
有了度量,就自然会诱导拓扑,我们在此先做个mark,在后面再回来看这个问题。
【本文为耀星会作者的原创作品,未经允许,禁止盗用、转载、篡改文章,否则耀星会和作者将追究版权责任。】

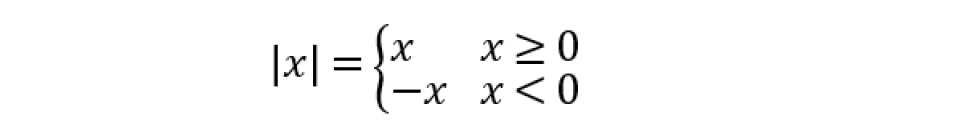
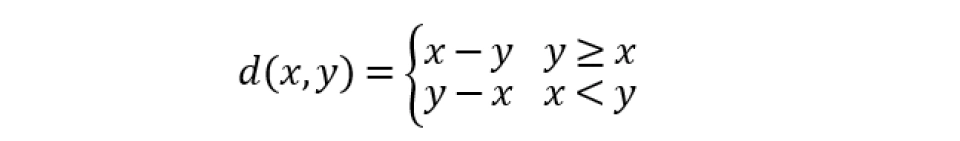

![[s-70]](https://www.bokeyuan.net/pic/image/emoji/cas/70.png)











