科普驿站 第八十二期
科目:数学
难度:B1
讲师:萌萌哒小西瓜
第二部分:整数与有理数(上)
在上一篇文章中,我们从集合论的角度严格地定义了什么是自然数,给出了自然数的一个构造,并在自然数集上定义了加法、乘法两个运算,此外我们还定义了大小关系。在这篇文章中,我们将会对加法和乘法两个运算进行深入的讨论,并将阐述整数和有理数。
代数结构:数学三大结构之一
Bourbaki(布尔巴基)学派,是上个世纪数学界最重要的学派之一,深刻地影响了数学和数学教育的走向。这一些来自法国的学者,认为整个现代数学完全基于集合论,他们认为数学是结构的艺术,只研究三种结构:代数结构、拓扑结构、序结构。他们的鸿篇巨著《数学原本》在当时的各个领域成为了标准性的参考书。当然,布尔巴基学派对数学的严谨性提出了严苛的要求,也一度对数学的教育产生了极坏的影响——对于中小学生而言,过分强调严谨性让很多人对数学敬而远之,也就没有多少勇气去学习了。
在这篇文章中,我们只介绍代数结构中最最简单的部分——事实上,即使是大学数学系开设的“抽象代数”课程,也只能揭露代数结构的冰山一角。
三种数学结构无非是给集合增添一些东西,序结构是给集合增添一个关系(例如大于小于)、拓扑结构是给集合添加一些包含关系,而代数结构就是给集合添加一个运算。所谓运算,在上一篇文章中我们已经提及了,运算本质是一个函数,是从S×S到S的映射。
举一些例子,在计算机上有一个重要的类型叫做布尔(Boolean)类型,对应了二进制,也是逻辑的基础。布尔类型只有两个取值,真(True,简记为T)和假(False,简记为F)。我们有这些运算:
1.与(and): T and T = T, T and F = F, F and T = T, F and F = F
2. 或(or): T or T = T, T or F = T, F or T = T, F or F = F
3. 异或(xor): T xor T = F, T xor F = T, F xor T = T, F xor F = F
4. 蕴含(to): T to T = T, T to F = F, F to T = T, F to F = T
可以看到,与、或、异或都满足交换律和结合律,与和或之间有分配律。数学家会把这样的结构提取出来,研究他们共同的性质。
定义:集合S与集合S上的运算⊕构成阿贝尔群(Abelian Group),如果满足下面五个要求:
1.运算是封闭的,即如果a∈S、b∈S,那么a⊕b∈S。
2.运算是结合的,即(a⊕b)⊕c=a⊕(b⊕c)。
3.存在零元e∈S,满足a⊕e=e⊕a=a。
4.对任意a∈S,存在负元-a∈S,满足a⊕(-a)=(-a)⊕a=e。(可以证明,只要存在,必然唯一。只要构造(-a)1⊕a⊕(-a)2,根据负元定义与结合律即可得到)。
5. 运算是交换的,即a⊕b=b⊕a。
事实上,如果满足前两个,(S,⊕)称为半群;满足前四个,(S,⊕)称为群。群是描述对称性的最有力工具,是现代数学和物理学的基础。两百年法国大数学家、天才Evariste Galois(埃瓦里斯特·伽罗瓦)在十几岁的时候系统地建立群-环-域的体系,并提出了伽罗瓦理论,完美地解决了困扰人类上千年的化圆为方、立方倍积、三等分角、五次以上求根公式等问题。可惜的是他后来为了爱情决斗而死,年仅21岁。
可以看到,({True,False},xor)是构成阿贝尔群的。
整数
现在我们考查(N,+),加法是具备结合律和交换律的,还有零元,也就是说(N,+)已经是个含零元的交换的半群了,离阿贝尔群仿佛只差了那么一点点——负元。
于是我们代数的定义这些形式元素,也就是负整数,与正整数一起构成整数。
我们一步一步地说明,首先我们可以定义自然数的减法(大减小):如果a≤b,则定义满足a+c=b的c为c=b-a。减法的存在性根据上一篇文章不等号的定义是显然的,唯一性请读者自行证明(提示:可以假设有两个,然后证明其有着相同的后继,采用Peano公理说明相等)。
我们形式的定义对任意n∈N∖{0}构造-n,并将全部-n构成的集合记作Z-。
我们记Z=N∪Z-,称之为整数集合。
我们定义整数的加法如下:(为表示区别,+Z为整数加法,+N为自然数加法,-表示前述定义了的大减小的整数加法)
a +N b a,b均为自然数
a-(-b) a为自然数,b不是自然数,a≥(-b)
a+zb= -((-b)-a) a为自然数,b不是自然数,a<(-b)
-b +z a a不是自然数,b为自然数
-((-a) +N (-b)) a,b均不是自然数
至此,整数关于加法,构成了阿贝尔群。
正有理数
自然数关于乘法仿佛也有很好的性质,但是如果我们也想把它做成阿贝尔群,就会有一个问题——显然这里的“零元”(或者说单位元)应该是1,而0⋅x=1这个方程我们倾向于没有解(事实上这里是有问题的,一些数学家一样引入了形式的定义,但这里不做展开)。所以我们只考查Z+=N∖{0}如何与乘法做成阿贝尔群。
首先我们固定“零元”为1,那么就得对每个n≠1构造“负元” 1/n ——当然,仍然是形式上的。我们需要定义乘法,虽然n⋅1/n =1/n ⋅n=1已经有了,但是还要考虑 1/n ⋅m这种问题。我们可以形式的定义
然后说形如 m/n 的数字构成正有理数Q+,并且定义整个正有理数上的乘法⋅Q
至此一切都是良定义的,但是你会发现 4/1、4/2、6/9 这样的“正有理数”——其实按照我们的构造方法,可从来没说 4/1=4、4/2=2、6/9=2/3 哦。
但是为了符合人的常识,我们额外要求
这样我们就有了阿贝尔群(Q+,⋅),为正有理数与乘法构成的。
【本文为耀星会作者的原创作品,未经允许,禁止盗用、转载、篡改文章,否则耀星会和作者将追究版权责任。】

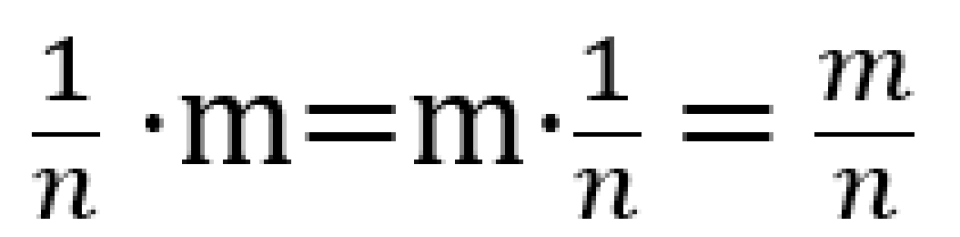
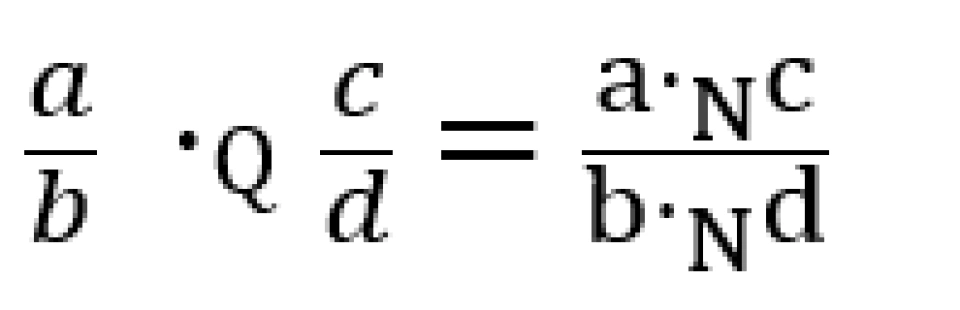
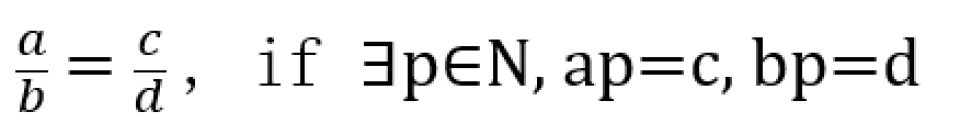

![[s-1]](https://www.bokeyuan.net/pic/image/emoji/cas/1.png)
![[s-70]](https://www.bokeyuan.net/pic/image/emoji/cas/70.png)











