科普驿站 第八十二期
科目:数学
难度:B1
讲师:萌萌哒小西瓜
第一部分:自然数
本系列科普文章就是特别为大家所编写的,面向高中生与非数学专业的大学生,介绍我们仿佛很熟知却其实也很陌生的数字——自然数、整数、有理数、无理数、实数和复数。与一般的科普不同,我在本系列文章的介绍中会进行一些深入的探讨、包含一部分证明,而不是简单的结论的展示(因为这些结论在中小学课程中已经广为人所熟知)。在阅读本系列文章前,有一个前置知识需要掌握:集合。集合也是构建整个现代数学的基础。
在本系列文章中,我们将穿插入数学的三大结构——代数结构、序结构、拓扑结构。作为科普,本系列文章不要求读者先前学过这些知识,只是以数这个“简单”的例子让读者对这些深入的数学内容进行一定的浅层次思考,引导读者去发现贯穿数学各个分支的结构之美。
什么是自然数?
我想,所有人看到这个问题,都会说:“西瓜,我知道啊,小学一年级就学过,自然数嘛,0、1、2、3、4、5……”。(曾经有一些课本认为0不是自然数,这个属于历史问题不做详细讨论。)可是如果问一下严格的定义,我相信今天绝大多数接受过高等教育的同学也会支支吾吾说不清楚。
翻开小学教材,都会这么说:“形如0、1、2、3、4、5的为自然数”——显然这不是一个严格定义。事实上,也许在几十万年甚至几百万年之前,当人类刚刚诞生,指着树上的苹果一个个数1、2、3的时候,自然数就已经出现了,但是真正给出严格定义的却是在1889年——至今只有一百多年的历史。那一年,意大利大数学家Giuseppe Peano(朱塞佩·皮亚诺)首先提出了自然数的五条公理,严格地定义了自然数,合称Peano公理:
1. 0是自然数(0∈N)
这说明自然数是存在的,至少不是空集。
2. 每一个确定的自然数a,都有一个确定的后继数a',a'也是自然数
这条公理说明,自然数至少有一条链,并且显然是无限延长的。
3. 对于每个自然数b、c,b=c当且仅当b的后继数=c的后继数
这条公理防止了树形结构的产生——比如说有3和3都是4的前驱,那么可以产生树状的分叉。至此,自然数只能是链条状的了——虽然还没有确定这个链条是一个方向延伸还是两个方向都能延伸,也没有告诉我们是否只有一根链条。
4. 0不是任何自然数的后继数
这条公理说明,至少0所在的链条是单方向无限延伸的——0就是起点。当然如果认为0不是自然数的,这里应该设置为1。
5. (数学归纳法)任意关于自然数的命题,如果证明:它对自然数0是真的,且假定它对自然数a为真时,可以证明对自然数a'也真,那么,命题对所有自然数都真。
这条公理说明了自然数只有一根链条,也就是从0开始的链条。
如果用更数学化的语言,自然数N=(S,e,f),其中S是所有自然数构成的集合,e是自然数0(公理1),f是映射f:S→S∖{e},将x映射为x的后继(公理2和公理4),此外还需要满足:f为单射(公理3),以及如果A为S的子集,且有e∈A和∀a∈A,f(a)∈A,那么A=S(公理5)。
用符号表达为:
1. e∈S
2. (∀a∈S)(f(a)∈S)
3. (∀b∈S)(∀c∈S)((f(b)=f(c))→(b=c))(思考:为什么原先的当且仅当这里变成了→?提示:什么是映射?)
4. (∀a∈S)(f(a)≠e)
5. (∀A⊆S)(((e∈A)∧(∀a∈A)(f(a)∈A))→(A=S))
怎样构造自然数?
我们定义了什么叫自然数,但是我们还缺少一个实际的案例。德国大科学家John von Neumann(约翰·冯·诺伊曼)给了一个绝妙的构造。冯·诺伊曼是一个真正意义上的天才,有过目不忘的记忆能力与心算无穷级数的计算能力,在数学(集合、算子、测度、几何、博弈、运筹等)、物理学、经济学领域都有重大的贡献,在计算机领域更是划时代的伟大开拓者——冯·诺伊曼提出的存储程序的设想,将计算机从预设功能的计算器中解放出来,称为“冯·诺伊曼架构”,沿用至今。晚年冯·诺伊曼投入了生物的大坑研究起了脑科学,却没有太突出的成就。
冯·诺伊曼认为,0=∅,那么对于x∈N,定义后继f(x)=x∪{x}。列表说明:
0=∅
1=∅∪{∅}={∅}={0}
2={∅}∪{{∅}}={{∅},∅}={0,1}
3={{∅},∅}∪{{{∅},∅}}={{{∅},∅},{∅},∅}={0,1,2}
如果定义Card(A)代表集合A的元素个数,那么可以发现,Card(n)=n,∀n∈N。
如何定义自然数上的运算与关系?
在本文中,我们先只定义加法和乘法——尽管我们在小学就学过加减乘除四种运算——减法和除法我将在下一篇文章中用一个更高纬度的思路去介绍。
加法是一个二元函数,可以认为+:N×N→N(这里的×为集合的笛卡尔积)。简单地说就是有函数f(a,b)=a+b。在Peano算术系统中,加法只需要两个公理递归定义即可:
1. a+0=a
2. a+S(b)=S(a+b),其中, S(x)代表x的后继。
例如
乘法也是一个二元函数,定义⋅:N×N→N,满足下述两个公理:
1. a⋅0=0
2. a⋅S(b)=a+(a⋅b),其中, S(x)代表x的后继
例如
其实从上面两个例子能看出来,加法和乘法的交换律本身不是显然的,请读者自行证明(留做习题答案略)。此外,结合律就更加的不明显了,但是分配律却相对显然些(都请读者自行证明)。
此外,对a,b∈N,我们定义a≤b当且仅当∃c∈N,a+c=b。
显然,≤关于+和⋅是稳定的,即如果a≤b,那么a+c≤b+c(由交换律和结合律)、a⋅c≤b⋅c(由分配律),当然现在还都局限在自然数集上,也就是说a,b,c∈N。
【本文为耀星会作者的原创作品,未经允许,禁止盗用、转载、篡改文章,否则耀星会和作者将追究版权责任。】


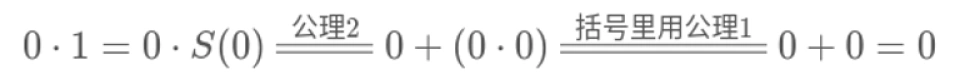


![[s-3]](https://www.bokeyuan.net/pic/image/emoji/cas/3.png)











