”千言万语不及一张图“—–基础概念
图论(Graph Theory)是离散数学的一个分支,它以图为研究对象。
图可用于在物理、生物、社会和信息系统中建模许多类型的关系和过程,许多实际问题可以用图来表示。因此,图论成为运筹学、控制论、信息论、网络理论、博弈论、物理学、化学、生物学、社会科学、语言学、计算机科学等众多学科强有力的数学工具。在强调其应用于现实世界的系统时,网络有时被定义为一个图,其中属性(例如名称)之间的关系以节点和或边的形式关联起来。
图是用来对对象之间的成对关系建模的数学结构,由”节点”或“顶点”(Vertex)以及连接这些顶点的“边”(Edge)组成,简单来说,图就是由若干个不同的点以及连结其中某些点的图形。
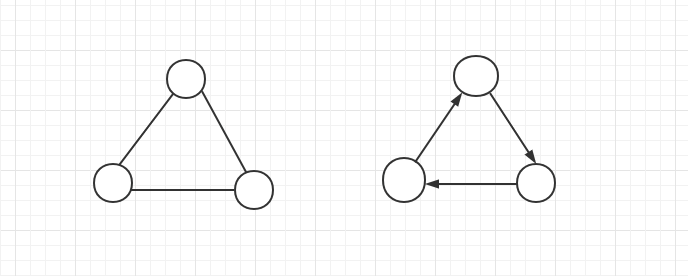
值得注意的是,图的顶点集合不能为空,但边的集合可以为空。图可能是无向的,这意味着图中的边在连接顶点时无需区分方向。否则,称图是有向的。下面左图是一个典型的无向图结构,右图则属于有向图。本章节介绍的图都是无向图。
一般来说,图均指简单图。
自环在图论中,自环( Loop )是一条 顶点与自身连接的边 。
图的连通性:在图论中,连通图基于连通的概念。在一个无向图 G 中,若从顶点 i 到顶点 j 有路径相连(当然从j到i也一定有路径),则称 i 和 j 是连通的。
在无向图中,关联一对顶点的无向边如果多于1条,则称这些边为平行边,平行边的条数称为重数。含平行边的图称为多重图,图中不包含自环不含平行边的图称为简单图(Simple graph)。简单图并不一定是无向图,也可以是有向图。简单来讲,简单图中可以有点不与其他点连线,但任一点不与自己连线,且任两点之间至多连一条线。
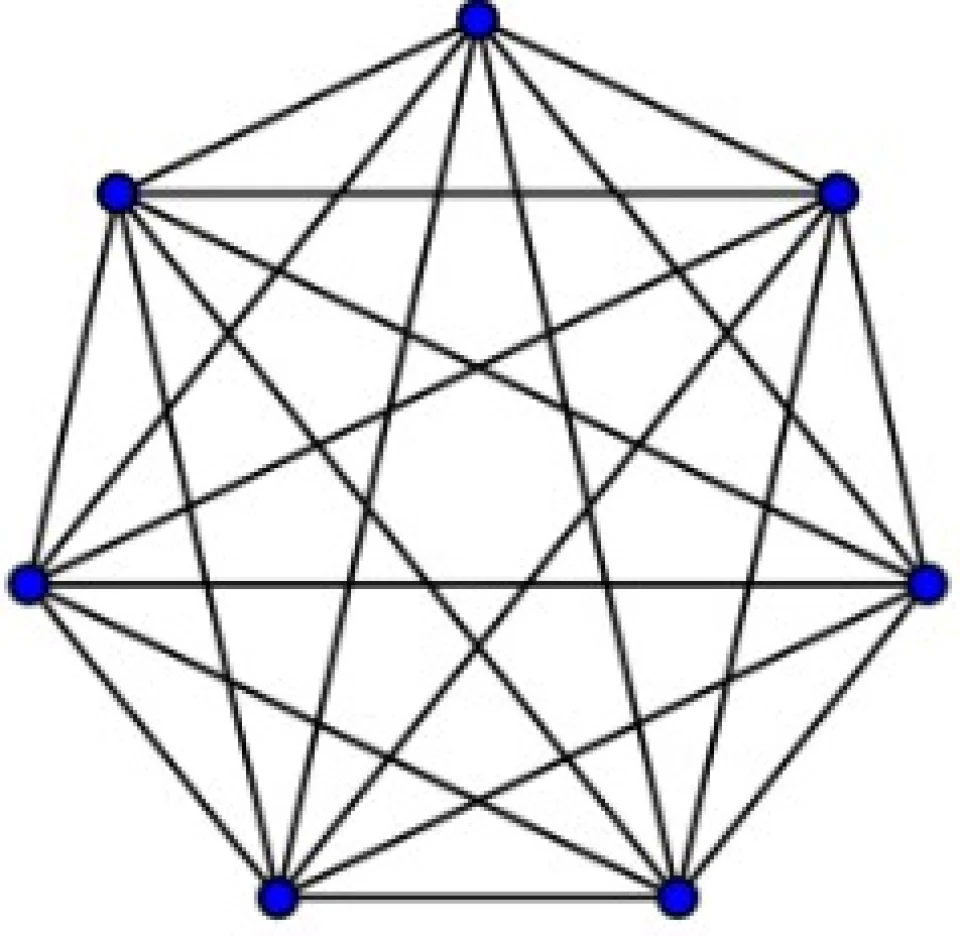
完全图完全图是一个简单的无向图,其中每对不同的顶点之间都恰连有一条边相连。下图就是一个完全图(complete graph)。
上述的图常用字母G表示,图G中的点,称为顶点(Vertex)所有顶点的集合记作V(G)或V;图G中的线,则称为边(Edge),所有边的集合记作E(G)或E.
请注意,这里说的图不涉及通常的几何性质,因此,图中顶点位置及边的曲直长短等,均无关紧要。我们仅关心图中顶点及边的数目,一个顶点引出了多少条边,哪些顶点之间有边相连(连通)等。
设V是一个顶点集合,x∈V是一个顶点,由x引出的边的条数非常重要,我们用d(x)表示这个数目,它称为x的次数(或度)
很多问题都可以改用图论的语言重述:用点表示所研究的对象,用连结一对的边表示对应的对象之间有某种关系,这就作出一个图。
(i)3,3,3,3,5,6,6,6,6,6;
(ii)1,1,3,3,3,3,5,6,8,9.
证明 我们将人用顶点表示.如果两人是朋友,就在对应的两个顶点之间连一条边.
各个顶点的次数之和应当等于边数的2倍(因为每条边被计算了两次).特别地,次数总和是一个偶数,但(i)中次数之和47却是一个奇数,因此统计有误。
(ii)中的数的和虽然是偶数42,但他们仍不能作为一个图的顶点的次数.因为次数为9的点与所有其他的点连边,它特别与两个次数为1的点连结了边.从而数为8的点不能与任一次数为1的点连边,这样,仅剩下7个点供连结,与次数8相违.证毕.
其实我们会得到一个基本结论:
这是图论中最基本的一个结论,它将实际与抽象联系在了一起。
发展历史
图论本身是应用数学的一部份,因此,历史上图论曾经被好多位数学家各自独立地建立过。关于图论的文字记载最早出现在欧拉1736年的论著中,他所考虑的原始问题有很强的实际背景。
众所周知,图论起源于一个非常经典的问题——哥尼斯堡(Konigsberg)问题。
1736年29岁的欧拉向圣彼得堡科学院递交了《哥尼斯堡的七座桥》的论文,在解答问题的同时,开创了数学的一个新的分支——图论与几何拓扑,也由此展开了数学史上的新历程。由此图论诞生。欧拉也成为图论的创始人。
这个问题的内容是:
18世纪初普鲁士的哥尼斯堡,有一条河穿过,河上有两个小岛,有七座桥把两个岛与河岸联系起来(如概述图)。有个人提出一个问题:一个步行者怎样才能不重复、不遗漏地一次走完七座桥,最后回到出发点。
大数学家欧拉把它转化成一个几何问题——一笔画问题(1.凡是由偶点组成的连通图,一定可以一笔画成。画时可以把任一偶点为起点,最后一定能以这个点为终点画完此图。2.凡是只有两个奇点的连通图(其余都为偶点),一定可以一笔画成。画时必须把一个奇点为起点,另一个奇点为终点。3.其他情况的图都不能一笔画出。(奇点数除以2便可算出此图需几笔画成。))。他不仅解决了此问题,且给出了连通图可以一笔画的充要条件是:奇点的数目不是0个就是2个(连到一点的数目如果是奇数条,就称为奇点;如果是偶数条,就称为偶点。要想一笔画成,必须中间点均是偶点,也就是有来路必有另一条去路,奇点只可能在两端。因此任何图能一笔画成,奇点要么没有,要么在两端)
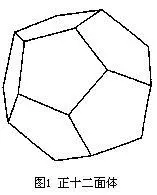
1859年,英国数学家汉密尔顿发明了一种游戏:用一个规则的实心十二面体,它的20个顶点标出世界著名的20个城市,要求游戏者找一条沿着各边通过每个顶点刚好一次的闭回路,即“绕行世界”。用图论的语言来说,游戏的目的是在十二面体的图中找出一个生成圈。这个生成圈后来被称为汉密尔顿回路。这个问题后来就叫做汉密尔顿问题。由于运筹学、计算机科学和编码理论中的很多问题都可以化为汉密尔顿问题,从而引起广泛的注意和研究,一百多年来对哈密顿问题的研究促进了图论的发展。这个问题在20实际70年代被证明是NP完全的。实际上对于节点数不到100的网络,利用现有最好的算法和计算机也需要几百年才能确定是否确定存在这样一条路径。
虽然四色定理证明了任何地图可以只用四个颜色着色,但是这个结论对于现实上的应用却相当有限。现实中的地图常会出现飞地,即两个不连通的区域属于同一个国家的情况(例如美国的阿拉斯加州),而制作地图时我们仍会要求这两个区域被涂上同样的颜色,在这种情况下,四个颜色将会是不够用的。
图论的广泛应用,促进了它自身的发展。20世纪40-60年代,拟阵理论、超图理论 、极图理论,以及代数图论、拓扑图论等都有很大的发展。
结语
本文还是花了我很多时间的,但是希望各位能在其中能够大概了解并大部分理解内容。感谢博科园,谢谢各位!
参考资料
离散数学(第六版) 耿素云、屈婉玲、张立昂 出版社 清华大学出版社 2021
图论中的一些概念_xsgaaa的博客-CSDN博客_图论 环


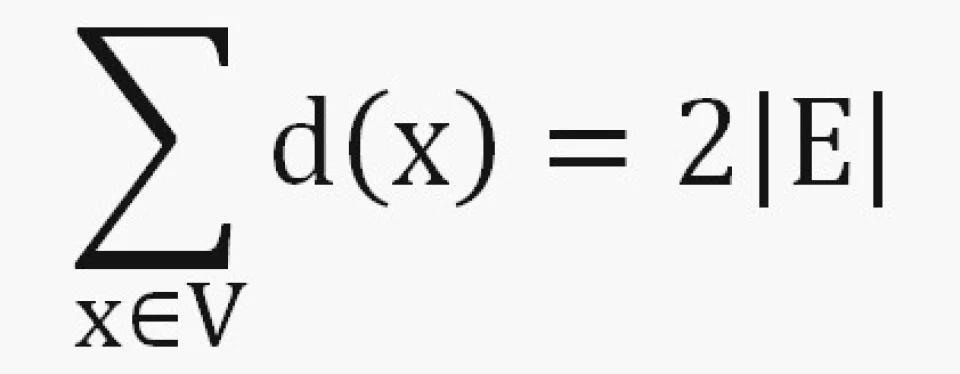












666