如果令x=sinθ,则有
即sin²θ sin⁴θ sin⁶θ …=(1-cos²θ)-1=tan²θ,sinθ≈θ,所以我将θ与sinθ代换,即
θ²+θ⁴+θ⁶+θ⁸+…≈(1/cos²θ)-1=tan²θ.
然后就有一个题:
若θ=π/100,求cosθ和tan²θ的近似值.
这里我先说明一下,为什么当θ足够小时(θ<π/36=5º)可认为sinθ≈θ,和那个常用幂级数,当然,证明的时候我尽量选取脍炙人口的方法:
①sinθ≈θ
方法一:
由泰勒公式得:
sinθ=θ-(θ³/3!) (θ⁵/5!)-(θ⁷/7!) …
其中n!=1×2×3×4×…×n
显然当θ足够小可以取θ≈sinθ.
方法二:
sinθ与θ是同阶无穷小,即sinθ/θ在θ→0时,它的极限等于1,所以当θ足够小时,可取sinθ=θ
②∑下标i=1,上标∞,代数式sin²ⁱθ=1/cos²θ-1=tan²θ
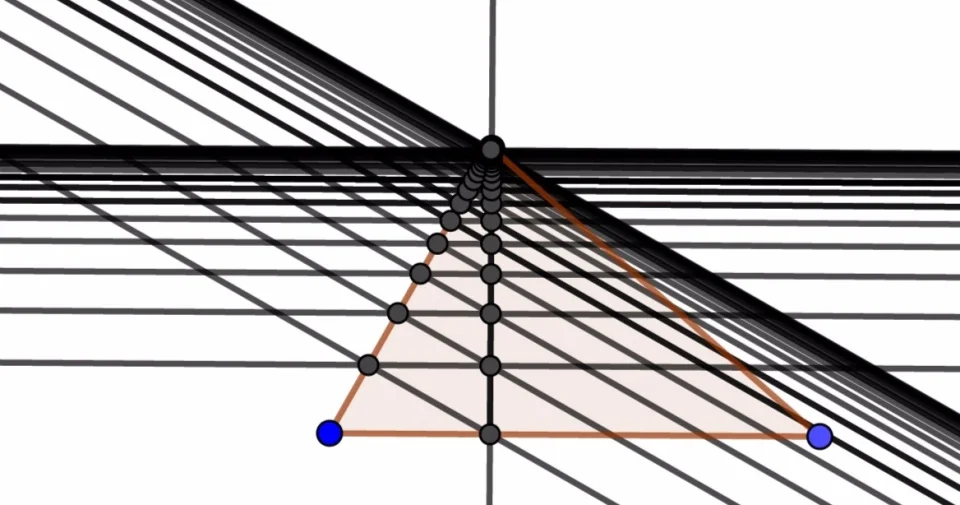
方法一(几何,这里相当于给等比数列求和极限找了一个几何表示):
三角形朝一个方向无限做高,把分成的所有小三角形加一起来与原三角形面积相等,进行化简(它们都相似所以它们面积有规律)
(就像这样,不断朝一个顶点方向做垂线,垂线会越来越密集)
方法二(代数):
首先
an=sin²ⁿθ
Sn=((an)q-a₁)/q-1
即Sn=(sinθ)^(2n+2)-sin²θ/sin²θ-1
数列收敛,所以可取极限
n→∞,
Sn=sin²θ/1-sin²θ
=1-cos²θ/cos²θ=(1/cos²θ)-1
=sin²θ/cos²θ
=tan²θ.
好了,序言讲完,接下来就是做题过程(你们先试着做一下,不全部算出来,用计算器算一下,并算一下误差):
(1)cosθ:用计算机算得
cos(π/100)≈0.999506560
i.∵cos²θ sin²θ=1
∴cos(π/100)=√(1-sin²(π/100))≈√(1-(π-100)²)
可用计算机算一下
约等于0.999506398
这里误差为1.62×10⁻⁷
ⅱ.∵θ² θ⁴ θ⁶ …≈(1/cos²θ)-1
∴cos(π/100)≈√(1/1 (π/100)² (π/100)⁴ (π/100)⁶ …)
我们先取第一项θ²
即cos(π/100)≈√(1/1 (π/100)²)
≈0.999506885
误差3.25×10⁻⁷
第二项θ⁴
同理得cos(π/100)≈0.999506398
误差为1.62×10⁻⁷
此时我们的值居然和第一种方法惊人的一致,可以看出法一在这里明显要简单一点,当然,他们之间有没有什么关系,可以用数学软件作图探究(求和本来就是一种函数)
(2)tanθ
tan(π/100)≈0.031426266
i.∵sin²θ/cos²θ=tan²θ,sin²θ cos²θ=1
∴
tan(π/100)≈√((π/100)²/1-(π/100)²)
≈0.031431441
误差ε₁=5.175×10⁻⁵
ⅱ.由上述可知
tan(π/100)≈√((π/100)² (π/100)⁴ (π/100)⁶ …)
我们可以分别取项算
取一项ε₂=1.034×10⁻⁵
取两项ε₃=0.516×10⁻⁵
取三项ε₄=0.518×10⁻⁵
取四项ε₅=0.518×10⁻⁵
从这里可以看出,第二种方法显然比第一种方法估算精确形式也简单
但是,第二种方法在第二项的时候却是估值最精确的,第三项第四项要比它大,这里可以用重要不等式x>sinx(x∈[0,1])来解释,该不等式可以构造函数求导证明
所以当取的项越多,误差越大,最终会不会比ε₁还要大呢?
谢谢大家!


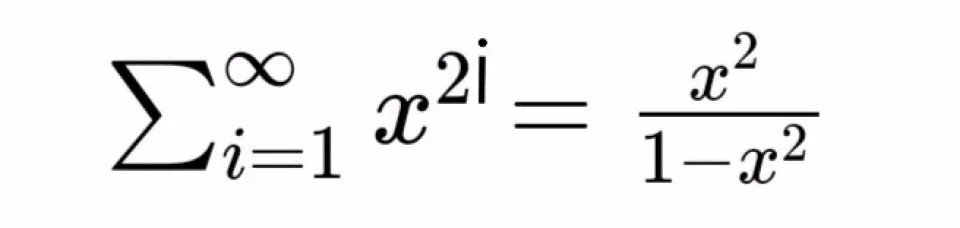
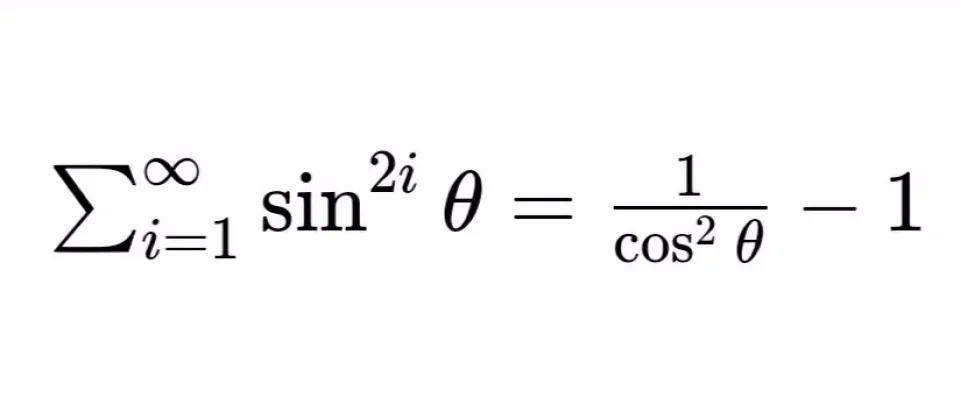

![[s-70]](https://www.bokeyuan.net/pic/image/emoji/cas/70.png)













